Основные этапы процесса нахождения корня нелинейного уравнения (3 видео)

Численное решение нелинейного уравнения. Этапы решения.

f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.

Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.

Задача нахождения корней состоит из 2 этапов:

1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.

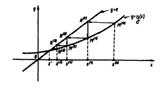
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:

[a;b] – интервал изоляции корня. Для каждого корня уравнения определяется интервал его изоляции [a;b]. На отрезке [a;b] должен находиться 1 корень.

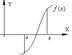
2. Уточнение корней – вычисление каждого корня с заданной степенью точности.

Классификация методов уточнения корней :

1) Метод половинного деления отрезка(дихотомии).

Отрезок [a;b], содержащий единственный корень, делят пополам, отбрасывают ту половину, где нет корня. Процесс повторяется до тех пор, пока длина отрезка не станет меньше заданной погр. E.

Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.

Построение последовательных хорд, в качестве приближений к корню принимаются значения их пересечения с осью абсцисс.

Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).

3) Метод касательных( метод Ньютона)

В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.

Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).

4) Комбинированный метод – объединение методов хорд и касательных.

Приближение к корню на каждой итерации происходит одновременно с 2 сторон интервала [a;b]. Одной стороны строится хорда, а с другой касательная.

Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).

5) Метод простой итерации.

Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.

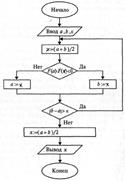
45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм. Требуется вычислить корень уравнения f(x)=0 на [a;b] с заданной погрешностью Е. Отрезок [a;b], содержащий единственный корень, делят на 2 половины, отбрасывают ту из них, где нет корня. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной погрешности Е.

Основные этапы процесса нахождения корня нелинейного уравнения

Алгоритм метода:

46)Уточнение корня нелинейного уравнения методом хорд. Схема алгоритма.Требуется вычислить корень уравнения f(x)=0 на [a,b] с заданной погрешностью е. Геометр-ки метод основан на построении последовательности хорд. Ур-е хорды . В данном методе процесс итерации состоит в том, что в качестве приближений к корню уравнение f(x)=0 принимаются значения х₁, х₂… х_i точек пересечения хорды АВ с осью абсцисс. Если f(a)>0 , то левая граница a неподвижна, х₀=b и из урав. хорды получим: Если f(a) 0 и f’’(x)>0 при a≤x≤b. Тогда для приближения к корню со стороны границы а используем построение хорды, а со стороны границы b – касательная. На 1й итерации строим хорду А₀В₀ и проводим касательную в точку В₀. Левую границу а переносим в а₁, правую – b_1. На каждой итерации для вычисления новых границ интервала используют ф-лы хорд и касательных : , . Сужение интервала проводим до тех пор пока он не станет

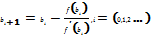
Видео:Метод половинного деления решение нелинейного уравненияСкачать

Этапы приближенного решения нелинейных уравнений.

Численные методы решения нелинейных уравнений.

Постановка задачи.

Пусть имеется уравнение вида

где f (x) — заданная алгебраическая или трансцендентная функция. (Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций — показательная, логарифмическая, тригонометрические, обратные тригонометрические.)

Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество, или доказать, что корней нет.

Если алгебраическое или трансцендентное уравнение достаточно сложно, то довольно редко удается точно найти его корни. Кроме того, в некоторых случаях уравнение может содержать коэффициенты, известные лишь приблизительно, поэтому сама задача о точном нахождении корней теряет смысл. В таких случаях применяют численные (приближенные) методы решения.

Поставим задачу найти такое приближенное значение корня x_пр, которое мало отличается от точного значения корня x*, так что выполняется неравенство │x* – x_пр │

Пример 1. Отделить графически корень уравнения .

Решение. Для решения задачи построим график функции (рис. 3).

Рис. 3. График функции .

Из рисунка видно, что один из корней уравнения принадлежит отрезку , второй – отрезку . Так как рассматриваемое уравнение имеет третью степень, то должен существовать еще один корень на интервале .

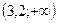
Пример 2. Отделить графически корень уравнения .

Решение. Преобразуем уравнение к виду и построим графики функций и (рис. 4).

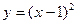
Рис. 4. Графическое отделение корней.

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку .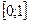

Аналитическое отделение корней основано на следующих теоремах.

Теорема 1. Если непрерывная функция принимает на концах отрезка значения разных знаков, т.е. , то на этом отрезке содержится по крайней мере один корень уравнения (1) (рис. 5).

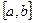
Рис. 5. Существование корня на отрезке.

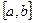
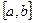
Теорема 2. Если непрерывная на отрезке функция принимает на концах отрезка значения разных знаков, а производная сохраняет знак внутри отрезка , то внутри отрезка существует единственный корень уравнения f (x) = 0 (рис. 6).

Рис. 6. Существование единственного корня на отрезке.

Пример 3. Подтвердить аналитически правильность нахождения отрезка изоляции корня уравнения .

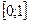
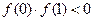
Решение. Для отрезка имеем: ; Значит, . Следовательно, корень отделён правильно.

Уточнение корней до заданной точности заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Наиболее распространенными являются метод деления отрезка пополам, метод касательных (Ньютона), метод секущих (хорд).

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Электронная библиотека

Приближенное решение уравнения состоит из двух этапов:

1) отделения корней, то есть нахождения интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения (3.1).

2) уточнения корней до заданной точности.

Отделение корней можно проводить графически и аналитически. Для того чтобы графически отделить корни уравнения (3.1), необходимо построить график функции y = f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения (рис. 3.1).

На практике же бывает удобнее заменить уравнение (3.1) равносильным ему уравнением:

где , – более простые функции, чем f(x).

Абсциссы точек пересечения графиков функций и дают корни уравнения (3.2), а значит и исходного уравнения (3.1) (рис. 3.2).

Аналитическое отделение корней основано на следующих теоремах:

Теорема 1. Если непрерывная функция y = f(x) принимает на концах отрезка значения разных знаков, т.е. , то на этом отрезке содержится, по крайней мере, один корень уравнения (3.1) (рис. 3.3).

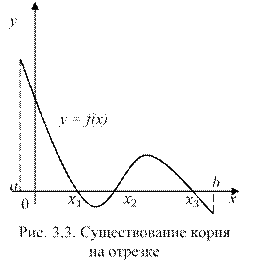
Теорема 2. Если непрерывная на отрезке функция y = f(x) принимает на концах отрезка значения разных знаков, а производная сохраняет знак внутри отрезка , то внутри отрезка существует единственный корень уравнения (рис. 3.4):

Уточнение корней до заданной точности заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Наиболее распространенными являются методы: деления отрезка пополам; касательных (Ньютона); секущих (хорд).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00