Основное уравнение релятивистской динамики вывод (7 видео)

Элементы релятивисткой динамики

Принцип относительности Эйнштейна утверждает инвариантность всех законов природы по отношению к переходу от одной инерциальной системе отсчета к другой. Отсюда следует, что уравнения, которые описывают законы природы, должны быть инвариантны относительно преобразований Лоренца.

Содержание

Импульс. Релятивистская масса
Движение релятивистской частицы
Связь между энергией и импульсом релятивистской частицы
Релятивистская динамика
Релятивистская энергия
Релятивистский импульс.
Связь энергии и импульса.
Релятивистское уравнение движения.
Релятивистская динамика. Связь между массой и энергией
📽️ Видео

Видео:Урок 431. Элементы релятивистской динамикиСкачать

Импульс. Релятивистская масса

Во время создания СТО теории, удовлетворяющей данному условию, она подразумевала уже существующую теорию электродинамики Максвелла. Уравнения вышли неинвариантными относительно преобразований Лоренца, что требовало пересмотра и уточнения законов механики.

Для этого Эйнштейн основывался на требованиях выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Чтобы он выполнялся во всех инерционных системах отсчета, следовало изменить определение импульса тела.

Классический импульс p → = m ν → заменяют релятивистским p → с массой m и скоростью движения ν → . Запись принимает вид:

p → = m ν → 1 — ν 2 c 2 = m ν → 1 — β 2 .

Если данное определение задействовать при решении, то закон сохранения суммарного импульса частиц выполнится во всех инерциальных системах, в которых есть связь с преобразованиями Лоренца. Когда β → 0 релятивистский импульс перейдет в классический.

Масса m считается фундаментальной характеристикой частицы. Она не зависит от выбора инерциальной системы отсчета, скорости движения.

Некоторые учебники трактуют это как массу покоя, обозначаемую m 0 . Позже вводилась релятивистская масса частицы m 0 1 — β 2 , которая зависела от скорости движения частицы. Современная физика отказывается от данных терминологий.

Запись основного закона релятивистской динамики материальной точки принимает вид, аналогичный второму закону Ньютона:

тогда p → примет значение релятивистского импульса частицы. Отсюда следует

F → = d d t m v → 1 — ν 2 c 2 .

Скорость частицы в релятивистской механике не пропорциональна релятивистскому импульсу, то есть скорость изменения не будет пропорциональна ускорению. Отсюда имеем, что сила постоянна по модулю и по направлению, причем не вызывает равноускоренного движения. Если существует одномерное движение вдоль О х , тогда ускорение частицы a = d ν d t с постоянной F равняется a = F m 1 — ν 2 c 2 3 2 .

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Движение релятивистской частицы

При росте скорости классической частицы под действием постоянной силы, скорость релятивистской частицы не превышает скорость света с в пустоте.

Это очевидно, так как выполняется закон сохранения энергии релятивистской частицы. Определение E k производится через работу внешней силы, которая необходима для сообщения телу заданной скорости. При разгоне частицы с массой m из состояния покоя до скорости ν 0 действует постоянная сила, совершающая работу

A = ∫ F · d x = ∫ F · ν · d t = ∫ m · α · ν · d t 1 — ν 2 c 2 3 2 .

Так как α d t = d ν , то запись примет вид E k = A = ∫ 0 v 0 m · ν · d ν 1 — ν 2 c 2 3 2 .

При вычислении интеграла произойдет упрощение выражения:

E k = m c 2 1 — ν 2 c 2 — m c 2 .

Интерпретация Эйнштейном первого члена правой части звучит как полная энергия Е движущейся частицы, а второго – энергией покоя E 0 :

E = m c 2 1 — ν 2 c 2 , E 0 = m c 2 .

Кинетической энергией E k считают разность между полной Е и энергией покоя E 0 . Запись принимает вид:

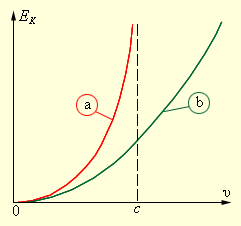
На рисунке 4 . 5 . 1 изображено изменение E k частицы, подчиняющейся классическому и релятивистскому законам.

Рисунок 4 . 5 . 1 . Зависимость кинетической энергии от скорости для релятивистской ( a ) и классической ( b ) частиц. При υ ≪ c оба закона совпадают.

Вывод релятивистской механики в том, что масса m, находящаяся в покое, содержит большое количество энергии. Это применяется при ядерной энергии. Если наблюдалось уменьшение массы частицы на ∆ m , тогда выделившаяся энергия примет вид ∆ E = ∆ m · c 2 . Проводимые эксперименты дают понять, что существование энергии покоя реальное. Первый, кто подтвердил это, был Эйнштейн. Он использовал отношение, связывающее массу и энергию, полученное при их сравнении. При бета-распаде свободного нейтрона появлялись протон, электрон и антинейтрино с нулевой массой:

Конечные продукты обладали суммарной кинетической энергией, равной 1 , 25 · 10 — 13 Д ж .

Масса нейтрона значительно превышает суммарную массу протона и электрона на ∆ m = 13 , 9 · 10 — 31 к г . Так как прослеживается уменьшение массы, необходимо использовать соответствующую энергию ∆ E = ∆ m · c 2 = 1 , 25 · 10 — 13 Д ж . Она равняется кинетической энергии релятивистской частицы.

Если взрывается 1 т тринитротолуола, то происходит освобождение энергии 4 , 2 · 10 9 Д ж , при взрыве мегатонной бомбы – 4 , 2 · 10 15 Д ж . Из формулы m = E c 2 выходит, что искомая масса – это 46 г . При взрыве ядерной бомбы m уменьшается на 50 г . То есть масса водородной бомбы при 1 мегатонне тринитротолуола имеет около 50 к г .

Видео:18. Релятивистская динамикаСкачать

Связь между энергией и импульсом релятивистской частицы

Самым важным выводом СТО является закон пропорциональности массы и энергии. Они обладают различными свойствами материи. Масса тела говорит о его инертности или способности вступать в гравитационное взаимодействие с другими телами. Важное свойство энергии – это способность превращения из одной формы в другую во время различных физических процессов, что подтверждает закон сохранения энергии.

Масса и энергия пропорциональны и выражают внутреннюю сущность материи.

Получаем, что формула Эйнштейна E 0 = m c 2 выражает фундаментальный закон природы, называемый законом взаимосвязи массы и энергии.

Если скомбинировать выражения p → = m ν → 1 — ν 2 c 2 = m ν → 1 — β 2 и E = m c 2 1 — ν 2 c 2 , то придем к связывающему их соотношению.

Для этого следует переписать эти формулы в упрощенном виде

p 2 m c 2 = ν 2 c 2 1 — ν 2 c 2 ,

E m c 2 2 = 1 1 — ν 2 c 2 .

После почленного вычитания получаем E 2 = m c 2 2 + p c 2 .

Следовательно, что для покоящихся частиц энергия фиксируется как E = E 0 = m c 2 .

Исходя из соотношения становится понятно, что частица может обладать энергией и импульсом, но не иметь массы, то есть m = 0 . Она получила название безмассовой. Для нее используется формула связи энергии и импульса в виде E = p c .

К частицам, которые не имеют массы, относят фотоны, называемые квантами электромагнитного излучения, и нейтрино. Существование безмассовых частиц в покое невозможно, поэтому их движение характеризуется предельной скоростью с .

Видео:Зависимость массы от скорости. Элементы релятивистской динамики | Физика 11 класс #34 | ИнфоурокСкачать

Релятивистская динамика

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: полная энергия, связь массы и энергии, энергия покоя.

В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.

Видео:Самое простое и понятное объяснение Специальной теории относительностиСкачать

Релятивистская энергия

Предположим, что изолированное тело массы покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:

Здесь — энергия тела, — скорость света в вакууме. Поскольку тело покоится, энергия , вычиляемая по формуле (1) , называется энергией покоя.

Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия

Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна Дж/кг, поэтому находим: кг . Это девять миллионов тонн!

Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.

Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.

Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину приводит к изменению массы тела на

Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой кг на (удельная теплоёмкость воды равна ) ей нужно передать количество теплоты:

Увеличение массы воды будет равно:

Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.

Формула ( 1 ) даёт энергию покоящегося тела. Что изменится, если тело движется?

Снова рассмотрим неподвижную систему отсчёта и систему , движущуюся относительно со скоростью . Пусть тело массы покоится в системе ; тогда энергия тела в системе есть энергия покоя, вычисляемая по формуле ( 1 ). Оказывается, при переходе в систему энергия преобразуется так же, как и время — а именно, энергия тела в системе , в которой тело движется со скоростью , равна:

Формула ( 2 ) была также установлена Эйнштейном. Величина — это полная энергия движущегося тела. Поскольку в данной формуле делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при .

Выражение для полной энергии ( 2 ) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.

1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства

Оно означает, что : скорость массивного тела всегда меньше скорости света.

2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке в формулу ( 2 ) её числитель обращается в нуль. Но энергия-то фотона ненулевая!

Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула ( 2 ) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.

Интуитивно чувствуется, что полная энергия ( 2 ) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при :

С помощью этих формул последовательно получаем из ( 2 ):

Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:

При формула ( 6 ) переходит в нерелятивистское выражение .

Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из ( 5 ), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!

Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана суммарная масса продуктов распада примерно на меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.

При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!

Рассмотрим в качестве примера два тела массы , летящих навстречу друг другу с одинаковой скоростью . В результате неупругого столкновения образуется тело массы , скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:

Мы видим, что, 2m’ alt=’M> 2m’ /> — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный , возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Релятивистский импульс.

Классическое выражение для импульса не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.

Пусть система движется относительно системы со скоростью (рис. 1 ). Два тела массы в системе летят навстречу друг другу с одинаковой скоростью . Происходит неупругое столкновение.

Основное уравнение релятивистской динамики вывод

Рис. 1. К закону сохранения импульса

В системе тела после столкновения останавливаются. Давайте, как и выше, найдём массу образовавшегося тела:

Теперь посмотрим на процесс столкновения с точки зрения системы . До столкновения левое тело имеет скорость:

Правое тело имеет скорость:

Нерелятивистский импульс нашей системы до столкновения равен:

После столкновения получившееся тело массы двигается со скоростью .
Его нерелятивистский импульс равен:

Как видим, , то есть нерелятивистский импульс не сохраняется.

Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы , двигающегося со скоростью , равен:

Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.

Импульс системы до столкновения:

Импульс после столкновения:

Вот теперь всё правильно: !

Видео:Якута А. А. - Механика - Релятивистский интервал. Диаграмма Минковского. Релятивистская динамикаСкачать

Связь энергии и импульса.

Из формул ( 2 ) и ( 7 ) можно получить замечательное соотношение между энергией и импульсом в теории относительности. Возводим обе части этих формул в квадрат:

Это и есть искомое соотношение:

Данная формула позволяет выявить простую связь между энергией и импульсом фотона. Фотон имеет нулевую массу и движется со скоростью света. Как уже было замечено выше, сами по себе энергия и импульс фотона в СТО найдены быть не могут: при подстановке в формулы ( 2 ) и ( 7 ) значений и мы получим нули в числителе и знаменателе. Но зато с помощью ( 8 ) легко находим: , или

В квантовой физике устанавливается выражение для энергии фотона, после чего с помощью формулы ( 9 ) находится его импульс.

Видео:Механика - Релятивистские эффекты. Релятивистская механикаСкачать

Релятивистское уравнение движения.

Рассмотрим тело массы , движущееся вдоль оси под действием силы . Уравнение движения тела в классической механике — это второй закон Ньютона: . Если за бесконечно малое время приращение скорости тела равно , то , и уравнение движения запишется в виде:

Теперь заметим, что — изменение нерелятивистского импульса тела. В результате получим «импульсную» форму записи второго закона Ньютона — производная импульса тела по времени равна силе, приложенной к телу:

Все эти вещи вам знакомы, но повторить никогда не помешает 😉

Классическое уравнение движения — второй закон Ньютона — является инвариантным относительно преобразований Галилея, которые в классической механике описывают переход из одной инерциальной системы отсчёта в другую (это означает, напомним, что при указанном переходе второй закон Ньютона сохраняет свой вид). Однако в СТО переход между инерциальными системами отсчёта описывается преобразованиями Лоренца, а относительно них второй закон Ньютона уже не является инвариантным. Следовательно, классическое уравнение движения должно быть заменено релятивистским, которое сохраняет свой вид под действием преобразований Лоренца.

То, что второй закон Ньютона ( 10 ) не может быть верным в СТО, хорошо видно на следующем простом примере. Допустим, что к телу приложена постоянная сила. Тогда согласно классической механике тело будет двигаться с постоянным ускорением; скорость тела будет линейно возрастать и с течением времени превысит скорость света. Но мы знаем, что на самом
деле это невозможно.

Правильное уравнение движения в теории относительности оказывается совсем не сложным.
Релятивистское уравнение движения имеет вид ( 11 ), где p — релятивистский импульс:

Производная релятивистского импульса по времени равна силе, приложенной к телу.

В теории относительности уравнение ( 12 ) приходит на смену второму закону Ньютона.

Давайте выясним, как же в действительности будет двигаться тело массы m под действием постоянной силы . При условии из формулы ( 12 ) получаем:

Остаётся выразить отсюда скорость:

Посмотрим, что даёт эта формула при малых и при больших временах движения.
Пользуемся приближёнными соотношениями при :

Формулы ( 14 ) и ( 15 ) отличаются от формул ( 3 ) и ( 4 ) только лишь знаком в левых частях. Очень рекомендую вам запомнить все эти четыре приближённых равенства — они часто используются в физике.

Итак, начинаем с малых времён движения. Преобразуем выражение ( 13 ) следующим образом:

При малых имеем:

Последовательно пользуясь нашими приближёнными формулами, получим:

Выражение в скобках почти не отличается от единицы, поэтому при малых имеем:

Здесь — ускорение тела. Мы получили результат, хорошо известный нам из классической механики: скорость тела линейно растёт со временем. Это и не удивительно — при малых временах движения скорость тела также невелика, поэтому мы можем пренебречь релятивистскими эффектами и пользоваться обычной механикой Ньютона.

Теперь переходим к большим временам. Преобразуем формулу ( 13 ) по-другому:

При больших значениях имеем:

Хорошо видно, что при скорость тела неуклонно приближается к скорости света , но всегда остаётся меньше — как того и требует теория относительности.

Зависимость скорости тела от времени, даваемая формулой ( 13 ), графически представлена на рис. 2 .

Рис. 2. Разгон тела под действием постоянной силы

Начальный участок графика — почти линейный; здесь пока работает классическая механика. Впоследствии сказываются релятивистские поправки, график искривляется, и при больших временах наша кривая асимптотически приближается к прямой .

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Релятивистская динамика. Связь между массой и энергией

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим, какой вид принимают законы Ньютона в случае релятивистской механики, в каких именно случаях следует применять не классическую ньютоновскую механику, а релятивистскую, а также познакомимся с одной из важнейших формул физики , которая связывает между собой массу и энергию.