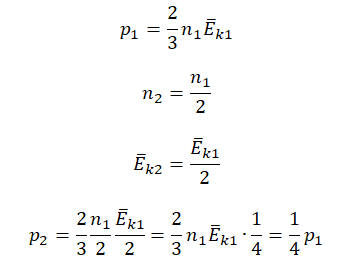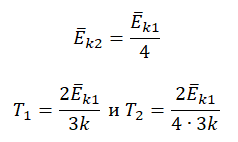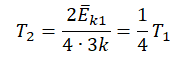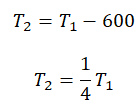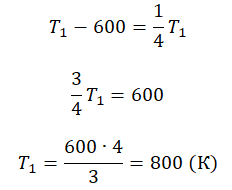Основное уравнение мкт связь между давлением и связь температуры и

Модель идеального газа считается самой простейшей относительно основных положений МКТ. Кинетическая модель идеального газа молекул говорит о том, что при взаимодействии между собой, шарики рассматриваются в качестве идеально упругих. Суммарный объем всех молекул достаточно мал по сравнению с объемом сосуда, в котором находится данный газ. Модель необходима для описания его поведения при различных давлениях и температурах.

Цель молекулярно-кинетической теории – установка связи между макроскопическими и макроскопическими параметрами.

После соударения молекул между собой и стенками сосуда происходит изменение направления движения и времени между интервалами столкновений. Модель идеального газа основывается на законах механики Ньютона, то тесть столкновения соответствуют закону упругого удара.

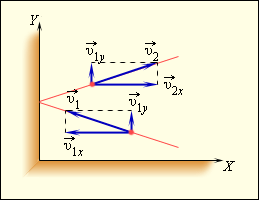
Чтобы определить давление газа на стенку сосуда, учитывается модель идеального газа. Исходя из этого, происходит возникновение сил, которые подчиняются 3 закону Ньютона. Отсюда получим, что проекция скорости υ x перпендикулярна относительно стенки, а знак меняется на противоположный. Проекция υ y параллельна и постоянна. Это показано на рисунке 3 . 2 . 1 .

Рисунок 3 . 2 . 1 . Упругое столкновение молекулы со стенкой.

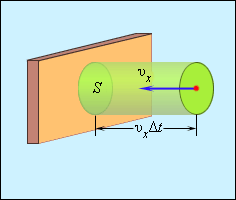
Отсюда следует, что изменение импульса можно записать в виде 2 m 0 υ x с массой молекулы, равной m 0 _. Необходимо выделить площадь S , как показано на рисунке 3 . 2 . 2 . По прошествии времени Δ t с S поверхностью столкнутся молекулы с проекциями скорости υ x _, которая направлена в сторону стены, и основанием цилиндра S с высотой υ x Δ t .

Рисунок 3 . 2 . 2 . Определение числа столкновений молекул с поверхностью S .

Если за единицу объема брать сосуд с n -ым количеством молекул, тогда их число в объеме цилиндра нужно обозначить, как n S υ x Δ t . Очевидно, что происходит столкновение только половины имеющихся молекул. Тогда количество ударов о S за время Δ t равняется 1 2 n S v x ∆ t .

При столкновении происходит изменение импульса 2 m 0 υ x . Тогда формула n m 0 v x 2 S ∆ t говорит о полном его изменении за определенный промежуток времени. Исходя из закона механики, изменение импульса всех молекул записывается как F Δ t . Силой F обозначается средняя сила, которая действует на молекулы. Но 3 закон Ньютона говорит о том, что аналогичная сила по модулю оказывает действие на поверхность S . Данное утверждение можно зафиксировать F ∆ t = n m 0 v x 2 S ∆ t .

Далее для упрощения следует разделить равенство на выражение S Δ t . Формула примет вид p = F S = n m 0 v x 2 со значением р , обозначаемым в качестве давления газа на стенку сосуда.

Все молекулы, находящиеся в сосуде на единицу объема, имеют разные проекции скоростей на ось О х . При столкновениях прослеживалось статистическое их распределение по скоростям, причем с разными направлениями векторов их скоростей.

Распределением Максвелла называют распределение молекул газа по модулю скоростей.

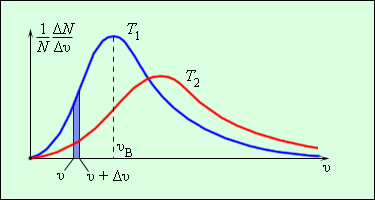
Еще в 1860 г Дж. Максвелл вывел закон распределения молекул газа по скоростям, основываясь на основных положениях молекулярно-кинетической теории молекулы. Рисунок 3 . 2 . 3 . наглядно показывает распределения молекул по скоростям с помощью кривых. На оси О х располагается модуль скорости, а на О у – количество молекул, находящихся на интервале от υ до υ + Δ υ . На рисунке 3 . 2 . 3 . данное значение выделено в виде столбика.

Рисунок 3 . 2 . 3 . Распределение молекул по скоростям. T 2 > T 1 .

Характерные параметры распределения Максвелла – это вероятная скорость υ в ,которая соответствует кривой распределения, и среднеквадратичная скорость υ к в = υ 2 → , где υ 2 → обозначающие среднее значение квадрата скорости.

Если растет температура, тогда максимум кривой будет смещен в сторону больших скоростей, то есть υ в и υ к в увеличатся.

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Распределение Максвелла

Для записи формулы давления газа необходимо предположить, что все молекулы разделены на n 1 , n 2 , n 3 группы с проекциями υ x 1 , υ x 2 , υ x 3 . Иначе говоря, записываем ∑ i n i = n . Можно зафиксировать, как n i m 0 v x i 2 . Тогда суммарное давление примет вид p = m 0 ∑ i n i v x i 2 .

Данная сумма является суммой квадратов проекций υ x всех n молекул на единичном объеме газа. При делении выражения на n получим среднее значение квадратичной скорости проекции υ x . Запишем в виде 1 n ∑ n i υ x i 2 = v x 2 → i .

Другая интерпретация формулы давления газа p = n m 0 v x 2 → . Все направления векторов различные, потому среднее значение квадратов проекций на координатные оси равняется v x 2 → = v y 2 → = v z 2 → = 1 3 v 2 → .

Формула для среднего давления газа на стенку сосуда обозначим, как p = p → = 1 3 n m 0 v 2 → = 2 3 n m 0 v 2 → 2 = 2 3 n E k → .

Из уравнения видна связь между р и m 0 и количеством молекул n , средней квадратичной скоростью v 2 → и средней кинетической энергией E k → молекул. Такое уравнение получило название уравнения молекулярно-кинетической уравнения теории газов.

Отсюда следует, что давление газа – это две трети средней кинетической энергии, которое имеется в единице объема. Основное уравнение молекулярно-кинетической теории газов или строения вещества содержит произведение количества молекул n на E k → . Предположительно сосуд имеет газ неизменного объема V , тогда n = N V = c o n s t ( N — число молекул в сосуде). Изменение давления происходит пропорционально изменению кинетической энергии.

Видео:Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Физика. Температура

Температура связана с понятием теплового равновесия. При контакте тела обмениваются энергией, которая передается и получает название количества теплоты.

Тепловым равновесием называют состояние системы тел, которые находятся в тепловом контакте с теплопередачей и с постоянными макроскопическими параметрами.

Температура — физический параметр, который находится в тепловом равновесии. Введение понятия температуры идет из нулевого закона термодинамики.

Температура измеряется с помощью термометра. Для его создания выбирается термометрическое вещество и величину, которая его характеризует. Разные конструкции подразумевают отличия в их свойствах.

Каждый термометр должен быть откалиброван. Использование природных систем с неизменной температурой необходимо для хорошего теплообмена. Температура плавления льда равняется 0 градусов Цельсия, а точка кипения воды – 100 градусов. Одно маленькое деление из шкалы равняется 1 градусу. Существует обозначение замерзания воды по Фаренгейту, то есть 32 ° F . Получаем, что формула примет вид T F = 9 5 T C + 32 или T C = 5 9 ( T F — 32 ) .

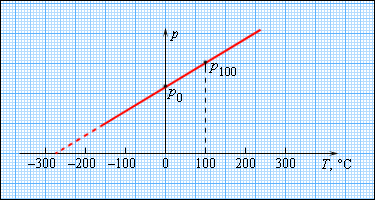
На рисунке 3 . 2 . 4 . изображен газовый термометр, который чаще всего заполняют разряженным гелием, воздухом с неизменным объемом, обозначаемым V = c o n s t , и давлением р . Из опыта видно, что возрастание давления идет с повышением температуры по Цельсию.

Рисунок 3 . 2 . 4 . Газовый термометр с постоянным объемом.

Видео:Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Температура кипения газов при давлении

Чтобы произвести калибровку газового термометра, следует выполнить измерение состояния молекул при 0 и 100 градусах. Для этого мы наносим точки p 0 и p 100 на график, после чего проводим прямую линию, как изображено на рисунке 3 . 2 . 5 . Получившийся калибровочный график способен определить температуру с разными значениями давления. При низких температурах возможно нахождение ее «гипотетической». Из опыта видно, что на свойства газа не влияет температура в — 273 , 15 ° С . При понижении температур газ переходит в жидкое или твердое состояние, поэтому получение охлажденного газа невозможно.

Рисунок 3 . 2 . 5 . Зависимость давления газа от температуры при V = c o n s t .

В 1848 году У. Кельвин предлагает использовать точку нулевого давления газа для составления шкалы. Отличие от измерений температуры в Цельсиях в том, что нулевая точка сдвинута на T К = T С + 273 , 15 .

По системе С И температура измеряется по Кельвину и обозначается К . Тогда комнатная температура запишется T С = 20 ° С , а по Кельвину – T К = 293 , 15 К .

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Температура кипения газов. Шкала Кельвина

Температурная шкала Кельвина считается абсолютной. Она наиболее приемлема для обозначения физических теорий.

Шкала Кельвина может быть не привязана двумя фиксированными точками, а именно: точка плавления льда и кипения воды с нормальным атмосферным давлением.

Нулевое давление называется абсолютным нулем температуры.

Шкала Кельвина имеет точку, в которой лед, вода и пар будут находиться в тепловом равновесии. Для калибровки других термометров применяют газовые, так как для практики они не подходят в виду своих больших размеров. Отсюда следует, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре, то есть p

T . Из опыта видно, что неизменный объем V и температура давления T прямо пропорциональны количеству вещества в сосуде к его объему: p

υ V = N N A V = n N A

n , где N принимает обозначение числа молекул в сосуде, а N А – постоянная Авогадро, n = N V – концентрации молекул.

После объединения соотношений получим, что запись примет вид p = n k T , где k считается универсальной постоянной величиной для всех газов, иначе говоря, постоянная Больцмана. Этот ученый являлся одним из создателей опытного обоснования основных положений молекулярно-кинетической теории. Ее обозначение в системе С И k = 1 , 38 ċ 10 – 23 Д ж / К .

При сравнении соотношения p = n k T с уравнением МКТ газов, получим E K → .

Средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна абсолютной температуре.

Температура является мерой для кинетической энергии молекул, которая не зависит от ее величины. Броуновская частица из жидкости и газа обладает аналогичной средней кинетической энергией, как и другая отдельная молекула. Это суждение верно для разномассовых молекул, находящихся в одном сосуде. Состояние равновесия говорит о том, что на них действуют одинаковые средние кинетические энергии, которые определяются температурой смеси. Запись давления смеси газов запишется как сумма парциальных давлений каждого из них: p = p 1 + p 2 + p 3 + … = ( n 1 + n 2 + n 3 + … ) k T .

Отсюда видно, что n 1 , n 2 , n 3 , … является концентрацией молекул газов в смеси. Выражение относят к молекулярно-кинетической теории, установленной Дальтоном: давление в смеси химически невзаимодействующих газов равняется сумме их парциальных давлений.

Видео:Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать

Изопроцессы, работа в термодинамике, первый закон термодинамики

Видео:Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Теория к заданию 8 из ЕГЭ по физике

Основное уравнение МКТ (давление газа)

Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.

Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.

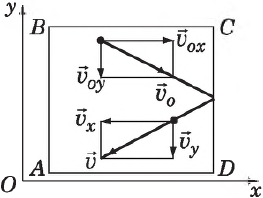
Определим давление газа на стенку площадью $S$ сосуда $ABCD$.

Каждая молекула массой $m_0$, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс $2m_υ_x$, где $υ_x$ — проекция скорости молекулы $υ↖$ на ось $О_х$, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен $2m_υ_Z$, где $Z$ — число таких столкновений (за $1$ с) всех молекул. Очевидно, что $Z=n=/$, где $n$ — концентрация молекул в единице объема; $N$ — число всех молекул. Число $Z$ пропорционально также скорости молекул $υ_x$ и площади стенки $S:Z∼nυ_S$. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости $υ_x$, только половина движется в сторону стенки $CD$ вторая половина — в сторону $АВ$ (т. е. в обратную). Поэтому $Z=/nυ_S$, а полный импульс, переданный стенке за $1$ с, равен $2m_nυ_x^S$. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе $F=/$, то $F=m_nυ_x^S$. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить: $F↖=<m_nυ_x^S>↖$.

Сила эта зависит, таким образом, от среднего квадрата скорости $<υ_x^>↖$.

Поскольку вследствие хаотичности движения все направления равноправны, то

С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:

Усредняя это выражение по всем молекулам и учитывая $υ^2=υ_x^+υ_y^+υ_z^$, получим:

С учетом последней формулы $F↖=/m_n↖$

Следовательно, давление на стенку сосуда равно:

Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.

Уравнение $p=/=/m_n↖$ позволяет получить связь между давлением и средней кинетической энергией молекул $↖=<m_↖>/:$

Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).

Абсолютная температура

Согласно основному уравнению МКТ, давление $р$ прямо пропорционально средней кинетической энергии $E↖$ поступательного движения молекул:

где $n$ — объемная концентрация молекул. Заменив в $p=/n↖$ $n$ отношением числа молекул $N$ к объему газа $V(n=/)$, получим:

В состоянии теплового равновесия при постоянном объеме средняя кинетическая энергия данной массы газа должна иметь вполне определенное значение, как и температура. Согласно формуле $/=/↖$, это означает, что отношение $/$ для данной температуры должно быть одним и тем же для любых идеальных газов. То, что это действительно так, было подтверждено экспериментально для разных газов, находящихся в условиях теплового равновесия при постоянном объеме (измерялось давление).

Таким образом, величина $Θ=/$, которую, в отличие от микропараметра $↖$, легко измерить, является вполне однозначной характеристикой теплового состояния газа, как и температура. Измеряется $Θ$ (как и энергия) в джоулях. Зависит она только от температуры и может рассматриваться как естественная мера температуры. Однако в силу укоренившейся привычки измерять температуру в градусах был введен коэффициент пропорциональности $k$ между температурой $Θ$, выраженной в энергетических единицах, и температурой $Т$, выраженной в градусах:

Температура $Т$, определяемая равенством $Θ=kT$, называется абсолютной температурой.

Значения температуры, определенной по формуле $/=/↖$, всегда положительны в силу положительности $Θ=/$ (ни давление, ни объем, ни число частиц отрицательными быть не могут). Поэтому минимальным значением температуры является нуль. Температура может равняться нулю, если давление либо объем равны нулю. Из принятого определения температуры следует, что нулем температуры является температура, при которой прекращается хаотическое движение молекул. Она называется абсолютным нулем температуры.

Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.

Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.

Единица абсолютной температуры является одной из семи основных единиц СИ и измеряется в кельвинах (обозначается буквой $К$).

Связь между температурами, измеренными по шкалам Цельсия $t$ и Кельвина $Т$, описывается формулой:

Абсолютный нуль равен $-273.15°$С. Как правило, при расчетах пользуются округленным значением абсолютного нуля ($-273°$С).

Коэффициент пропорциональности к в формуле $Θ=kT$ называется постоянной Больцмана в честь Л. Больцмана — одного из основателей молекулярно-кинетической теории газа. Этот коэффициент составляет $k=1.38^$ Дж/К.

Постоянная Больцмана связывает температуру $Θ$ в энергетических единицах с температурой $Т$ в кельвинах. Это одна из наиболее важных постоянных в молекулярно-кинетической теории.

Температура как мера кинетической энергии

Из основного уравнения молекулярно-кинетической теории, записанного в форме $p=/↖$

и определения абсолютной температуры согласно $/=kt$

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.

Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.

Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.

Уравнение $р = nkТ$

Из формулы $p=/n↖$ может быть получена зависимость давления газа от абсолютной температуры $Т$ и концентрации его молекул, если воспользоваться выражением для средней кинетической энергии:

где $k$ — постоянная Больцмана.

Из формулы $p=nkT$ очевидно, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова.

Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Средняя скорость теплового движения молекул может быть также выражена через абсолютную температуру, если в формуле $E↖=/kT$ заменить $E↖$ на $<m_↖>/$:

Квадратный корень из этой величины называется средней квадратичной скоростью:

Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)

Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением $р$, объемом $V$ и абсолютной температурой $Т$, определяющими его состояние:

где $В$ зависит от массы газа $m$ и его молекулярной массы $М$. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.

В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: $pV=RT$, где $R$ — универсальная газовая постоянная. Если молярная масса газа $М$, то

Уравнение состояния в форме $pV=/RT$ называется уравнением Клапейрона-Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля—Мариотта, Авогадро, Шарля.

Уравнение состояния $pV=/RT$ может быть получено из зависимости давления от температуры $p=nkT$, если в нее подставить концентрацию молекул $n$ из выражения

где $N_А$ — постоянная Авогадро, $N$ — число молекул в теле.

В результате получим:

Внутренняя энергия идеального одноатомного газа

Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома $E↖=/kT$ на число атомов $N=/N_A$.

Учитывая, что $kN_A=R$, получим значение внутренней энергии идеального газа:

Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.

Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:

Следует отметить, что, согласно выражению для средней кинетической энергии одного атома $(E↖=/kT)$ и в силу хаотичности движения, на каждое из трех возможных направлении движения или каждую степень свободы по оси $X,Y$ и $Z$ приходится одинаковая энергия $/$.

Число степеней свободы — это число возможных независимых направлений движения молекулы.

Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трем направлениям, поэтому общее число возможных направлений движения — $6$. За счет связи между молекулами число степеней свободы уменьшается на одну, поэтому число степеней свободы для двухатомной молекулы равно пяти.

Средняя кинетическая энергия двухатомной молекулы равна $/kT$. Соответственно внутренняя энергия идеального двухатомного газа равна:

Формулы для внутренней энергии идеального газа можно обобщить:

где $i$ — число степеней свободы молекул газа ($i = 3$ для одноатомного и $i=5$ для двухатомного газа).

Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).

Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).

Изопроцессы в газах

Изопроцессами называются процессы, протекающие при неизменном значении одного из параметров: давления ($р$), объема ($V$), температуры ($Т$).

В идеальном газе эти процессы подчиняются газовым законам.

Газовыми законами называются количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра.

Закон Бойля-Мариотта

Закон Бойля-Мариотта — один из основных газовых законов, он описывает изотермические процессы в газе.

Процесс изменения состояния термодинамической системы при постоянной температуре называется изотермическим.

Для данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.

$pV=const$ при $T=const$

Этот закон был экспериментально открыт английским ученым Р. Бойлем в 1662 г., в 1676 г. его сформулировал также французский ученый Э. Мариотт.

Закон строго выполняется только для идеальных газов. Для реальных газов он выполняется достаточно хорошо при небольших давлениях и высоких температурах. Так, при давлении $100$ атм. и температуре $0°$С отклонение измеренного значения $рV$ от расчетного составляет $7%$. Закон Бойля-Мариотта, как и другие газовые законы, является следствием уравнения состояния идеального газа.

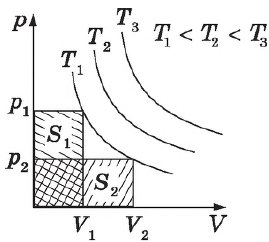
Графики зависимости $p(V)$ при $T=const$ ($p=/$) называются изотермами и представляют собой равносторонние гиперболы (площади $S_1=S_2$). Чем выше температура, тем выше лежит соответствующая ей изотерма.

Закон Шарля

Давление $p$ данной массы газа при постоянном объеме пропорционально температуре.

$p=constT$ при $T=const$

Закон был открыт французским физиком Ж. Шарлем в 1787 году.

Процесс изменения состояния термодинамической системы при постоянном объеме называется изохорным (от греч. hora — пространство).

Закон Шарля, как и другие газовые законы, является следствием уравнения состояния идеального газа:

Согласно $

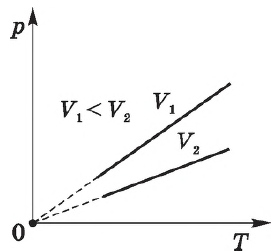
/=const$ при $V=const$, давление газа линейно зависит от температуры при постоянном объеме. Эта зависимость изображается прямой, которая называется изохорой. С ростом объема газа при постоянной температуре давление его, согласно закону Бойля—Мариотта, падает. Поэтому изохора, соответствующая большему объему, лежит ниже изохоры, соответствующей меньшему объему.

В соответствии с $

/=const$ при $V=const$, все изохоры начинаются в точке $Т=0$ (давление идеального газа при абсолютном нуле равно нулю).

Изохорный процесс используется в газовых термометрах постоянного объема.

Закон Гей-Люссака

При постоянном давлении $р$ объем $V$ идеального газа меняется линейно с температурой.

где $V_0$ — начальный объем, $t$ — разность начальной и конечной температур. Коэффициент теплового расширения идеальных газов $α=(/)K^$ одинаков для всех газов.

Процесс изменения состояния термодинамической системы при постоянном давлении называется изобарным (от греч. baros — вес, тяжесть).

Закон открыт французским ученым Ж. Гей-Люссаком в 1802 г. и независимо от него Дж. Дальтоном в 1801 г.

Закон Гей-Люссака, как и другие газовые законы, является следствием уравнения состояния идеального газа. Это становится очевидным, если в $V=V_0(1+αt)$ заменить $t$ абсолютной температурой $T=t+273.15$, а коэффициент расширения $α$ — его численным значением $/$:

Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.

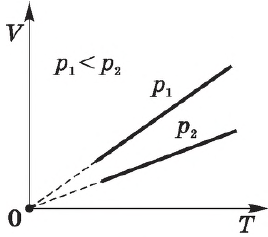
Согласно $/=const$ при $p=const$, объем газа линейно зависит от температуры при постоянном давлении:

Эта зависимость графически изображается прямой, которая называется изобарой.

Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре, согласно закону Бойля—Мариотта, уменьшается, поэтому изобара, соответствующая более высокому давлению $р_2$, лежит ниже изобары, соответствующей более низкому давлению $р_1$.

В области низких температур все изобары идеального газа сходятся в точке $Т=0$, но это не означает, что объем реального газа действительно обращается в нуль. При низких температурах все газы обращаются в жидкости, а к жидкостям уравнение состояния не применимо.

Видео:Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Основное уравнение МКТ идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Видео:Физика. МКТ: Основное уравнение МКТ. Центр онлайн-обучения «Фоксфорд»Скачать

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 o C).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

Если особо важна точность, следует использовать более точную формулу:

Пример №1. Температура воды равна o C. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Видео:Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p = 2 3 . . n − E k

p — давление идеального газа, n — концентрация молекул газа, − E k — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p = 1 3 . . m 0 n − v 2

m 0 — масса одной молекулы газа;

n — концентрация молекул газа;

− v 2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

p = 1 3 . . ρ − v 2

ρ — плотность газа

k — постоянная Больцмана (k = 1,38∙10 –3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Видео:Физика 10 класс (Урок№19 - Температура. Энергия теплового движения молекул.)Скачать

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v = √ 3 k T m 0 . . = √ 3 R T M . .

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R = N A k = 8 , 31 Д ж / К · м о л ь

Температура — мера кинетической энергии молекул идеального газа:

Полная энергия поступательного движения молекул газа определяется формулой:

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Составим систему уравнений:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

🎬 Видео

10 класс, 2 урок, Основное уравнение молекулярно кинетической теорииСкачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Основное уравнение МКТ | ФизикаСкачать

физика 10-11 база. лекция 9. Молекулярная физика. Температура и давления с позиций МКТ.Скачать

20. Основное уравнение МКТСкачать

Идеальный газ. Основное уравнение МКТСкачать

Основное уравнение МКТСкачать

Разбор 9 задания на основное уравнение МКТ за 8 минут | Физика ЕГЭ 2022 | PartaСкачать

10 класс, 3 урок, Температура в молекулярно кинетической теории газовСкачать