P — давление газа.
m — масса молекулы.
n — концентрация молекул.
-средний квадрат скорости.
Формула связывает микроскопическую величину — давление, которое может быть измерено манометром, c микроскопическими величинами, характеризующими молекулы.
m n = ρ (2)
ρ — плотность газа
Давление выражаем через его плотность: (3)
Средняя кинетическая энергия поступательного движения молекул:
Давление идеального газа пропорционально произведению числа молекул в единице объема на среднюю кинетическую энергию поступательного движения молекулы.
- Основное уравнение молекулярно-кинетической теории (Ерюткин Е.С.)
- Уравнение МКТ идеального газа — основные понятия, формулы и определение с примерами
- Основное уравнение МКТ идеального газа
- Микроскопические и макроскопические параметры
- Какой газ называют идеальным
- Основное уравнение МКТ идеального газа
- Пример решения задачи
- 🎬 Видео
Видео:Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Основное уравнение молекулярно-кинетической теории (Ерюткин Е.С.)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Как уже было сказано ранее, начиная с этого урока, мы приступаем к изучению только газов. На прошлом уроке мы дали представление о способах количественного описания некой порции вещества. Сейчас же мы начнём описывать газ со стороны его качественных характеристик (микро- и макропараметров). Мы сформулируем понятие об идеальном газе, опишем его параметры и введём соотношение, связывающее эти параметры (основное уравнение МКТ).
Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение МКТ идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Фазовые состояния вещества:
В МКТ различают три фазовых (агрегатных) состояния вещества: жидкое, кристаллическое, газообразное (существует и четвертое состояние — плазма, и оно самое распространенное во Вселенной, ведь именно в состоянии плазмы находится вещество в звездах). Изменение фазового состояния называют фазовым переходом. Рассмотрим разные фазовые состояния вещества и выясним особенности движения и взаимодействия молекул вещества в разных состояниях.
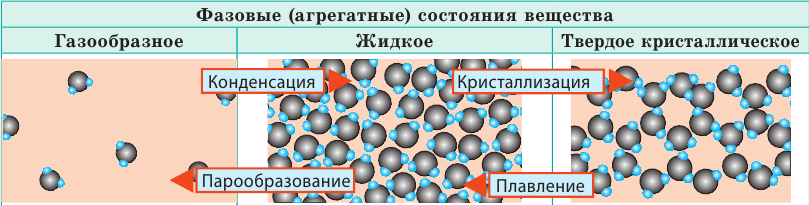 | ||
| Слово «газ» происходит от греческого слова chaos («хаос»). Молекулы газов расположены беспорядочно и на расстояниях, которые в десятки раз больше размеров самих молекул. На таких расстояниях молекулы практически не взаимодействуют друг с другом. Непрерывно сталкиваясь, молекулы газов разлетаются во все стороны, пока не встретят какое-либо препятствие, например стенки сосуда. Именно поэтому газы не имеют формы и занимают весь предоставленный объем. Большими расстояниями между молекулами объясняется и тот факт, что газы легко сжимаются. | Молекулы жидкости в целом расположены хаотично, однако в расположении ближайших молекул сохраняется определенный (ближний) порядок. Среднее расстояние между молекулами примерно равно размерам молекул, и межмолекулярные силы удерживают их около положения равновесия. Каждая молекула жидкости некоторое время (порядка 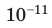 | В веществе, находящемся в твердом кристаллическом состоянии, молекулы расположены в определенном порядке (образуют кристаллическую решетку) на расстояниях, примерно равных размерам самих молекул, поэтому силы межмолекулярного взаимодействия удерживают их около положения равновесия. В отличие от жидкостей, перескакивания молекул в твердых телах происходят очень редко — каждая молекула сохраняет положение равновесия достаточно долго, а ее движение сводится к колебаниям около этого положения. Поэтому твердые тела сохраняют и объем, и форму; как и жидкость, их очень трудно сжать. |
Молекулы некоторых твердых тел в целом расположены беспорядочно. Такое состояние вещества называют аморфным. Вещества в аморфном состоянии напоминают очень вязкие жидкости. Так, если положить в сосуд кусочки смолы (аморфное вещество), со временем смола сольется и примет форму сосуда.
В отличие от кристаллических, аморфные вещества не имеют определенной температуры плавления, а переходят в жидкое состояние постепенно размягчаясь. Аморфное состояние веществ неустойчиво — постепенно происходит кристаллизация. Так, стекло имеет аморфную структуру, но со временем в нем образуются помутнения — кристаллики кварца. Сахар — это молекулярный кристалл. Если его расплавить и охладить, получим леденец — аморфное состояние сахара. Но через некоторое время в леденце начнут расти кристаллики сахара. Именно по этой причине засахаривается варенье.
- Молекулы, атомы, ионы находятся в непрерывном хаотическом движении. Именно движением частиц вещества можно объяснить такие явления, как броуновское движение (видимое в микроскоп хаотическое перемещение малых макрочастиц, взвешенных в жидкости или газе) и диффузия (взаимное проникновение соприкасающихся веществ друг в друга).
- Частицы вещества взаимодействуют друг с другом. Основная причина межмолекулярного взаимодействия — электрическое притяжение и отталкивание заряженных частиц, образующих атом. На расстояниях, которые больше размеров молекул, молекулы притягиваются друг к другу; на расстояниях, которые незначительно меньше размера молекул, — отталкиваются.
- Вещество может находиться в твердом, жидком и газообразном фазовых (агрегатных) состояниях в зависимости от того, как расположены, как двигаются и как взаимодействуют его частицы.
Видео:Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Основное уравнение МКТ идеального газа
Каждое макроскопическое тело состоит из огромного количества молекул. МКТ рассматривает строение и свойства макроскопических тел, а также процессы, происходящие в этих телах, с точки зрения их молекулярной структуры. Поведение макроскопических тел описывается рядом физических величин — микроскопическими и макроскопическими параметрами. Выясним, что это за параметры и как они связаны.
Микроскопические и макроскопические параметры
Рассмотрим систему, состоящую из очень большого количества атомов или молекул. Такой системой, например, может быть какой-либо газ. В любой момент времени каждая микрочастица газа обладает энергией, движется с некоторой скоростью, имеет массу.
Физические величины, характеризующие свойства и поведение отдельных микрочастиц вещества, называют микроскопическими параметрами.
Некоторые микроскопические параметры могут изменяться без внешнего воздействия на систему. Например, скорости движения молекул газа непрерывно изменяются в результате их столкновений друг с другом.
В то же время газ данной массы занимает некоторый объем, создает давление, имеет температуру. Значения этих физических величин определяются совокупностью множества молекул — например, мы не можем говорить о давлении, температуре или плотности одной молекулы.
Физические величины, характеризующие свойства и поведение макроскопических тел без учета их молекулярного строения, называют макроскопическими параметрами.
Макроскопические параметры могут изменяться только за счет внешних воздействий на систему или за счет теплообмена. Так, чтобы увеличить давление газа, газ нужно нагреть (передать определенное количество теплоты) или сжать (то есть совершить работу).
Какой газ называют идеальным
Количественные закономерности, связывающие макроскопические и микроскопические параметры тел, достаточно сложны. Рассмотрим самый простой случай — достаточно разреженные газы (такими, например, являются обычные газы при нормальных условиях). В разреженных газах расстояние между молекулами во много раз превышает размеры самих молекул, поэтому эти молекулы можно считать материальными точками, а их взаимодействием, за исключением моментов соударения, можно пренебречь. Кроме того, свойства разреженных газов практически не зависят от их молекулярного состава, а столкновения молекул такого газа приближаются к упругим. Таким образом, вместо реальных газов можно рассматривать их физическую модель — идеальный газ.
Идеальный газ — это физическая модель газа, молекулы которого принимают за материальные точки, не взаимодействующие друг с другом на расстоянии и упруго взаимодействующие в моменты столкновений.
Основное уравнение МКТ идеального газа
Начнем с такого микроскопического параметра, как скорость движения молекул. Обратим внимание на то, что бессмысленно рассматривать движение каждой отдельной молекулы и устанавливать скорость ее движения в данный момент времени, да это и невозможно: число молекул огромно, и за секунду каждая молекула изменяет скорость своего движения миллиарды раз. Поэтому физики используют средние значения скоростей молекул. Важнейшим в МКТ является понятие средний квадрат скорости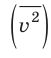
где N — число молекул; 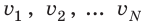
Квадратный корень из среднего квадрата скорости называют средней квадратичной скоростью движения молекул (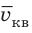
Понятно, что средний квадрат скорости (а следовательно, и среднюю квадратичную скорость) невозможно определить с помощью прямых измерений. Однако эта величина связана с определенными макроскопическими (измеряемыми) параметрами газа, например с давлением.
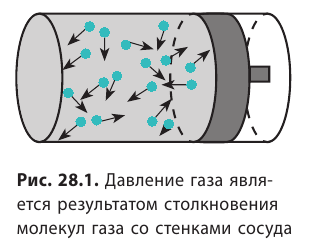
Напомним, что давление газа обусловлено ударами его молекул (рис. 28.1). Находясь в непрерывном хаотическом движении, молекулы газа сталкиваются со стенками сосуда и поверхностью любого тела в газе, действуя на них с некоторой силой. Суммарная сила воздействия частиц на единицу площади поверхности и есть давление газа: 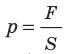
Уравнение зависимости давления p идеального газа от массы 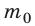
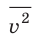
Здесь n — концентрация молекул газа — физическая величина, равная числу молекул в единице объема газа:
Средняя кинетическая энергия поступательного движения молекул идеального газа (кинетическая энергия поступательного движения, в среднем приходящаяся на одну молекулу) равна: 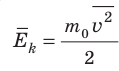
Пример решения задачи
Определите плотность идеального газа, находящегося под давлением 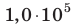
Решение:
В задаче нужно найти макроскопический параметр — плотность газа. Для решения задачи воспользуемся основным уравнением МКТ идеального газа:
Поскольку ρ = 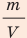
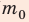
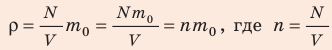
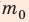
Отсюда 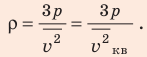
Проверим единицу, найдем значение искомой величины:
Анализ результата. Плотности газов при нормальных условиях колеблются от 0,09 до 1,5 кг/м3, то есть получен реальный результат.
Ответ: ρ = 1, 2 кг/м3.
- Физические величины, характеризующие свойства и поведение отдельных микрочастиц вещества, называют микроскопическими параметрами. Физические величины, характеризующие свойства и поведение макроскопических тел без учета их молекулярного строения, называют макроскопическими параметрами.
- Идеальный газ — это физическая модель газа, молекулы которого принимают за материальные точки, не взаимодействующие друг с другом на расстоянии и упруго взаимодействующие в момент столкновения.
- Основное уравнение МКТ идеального газа связывает макроскопический параметр (давление) с микроскопическими параметрами (массой и средним квадратом скорости движения молекул):
. Это уравнение можно записать в виде:
.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать

Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Физика. МКТ: Основное уравнение МКТ. Центр онлайн-обучения «Фоксфорд»Скачать

10 класс, 2 урок, Основное уравнение молекулярно кинетической теорииСкачать

#3 Идеальный газ + РЕШЕНИЕ ЗАДАЧ. Основное уравнение МКТ. Давление газа.Скачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. Практическая часть.10 классСкачать

Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Тема 2. Макро и микропараметры. Идеальный газ. Основное уравнение МКТ идеального газаСкачать

Физика 10 класс : Основное уравнение молекулярно-кинетической теории идеального газаСкачать

Вывод основного уравнения молекулярно кинетической теории.Скачать

Физика. 10 класс. Идеальный газ. Основное уравнение теории газов /19.11.2020/Скачать

Молекулярно-кинетическая теория | ЕГЭ по физике 2023 | Снежа Планк из ВебиумСкачать

Основные положения молекулярно-кинетической теории | Физика 10 класс #24 | ИнфоурокСкачать


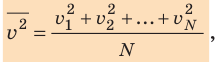
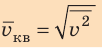
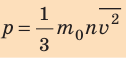
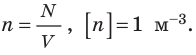
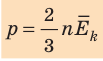
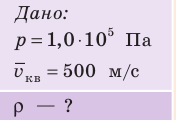


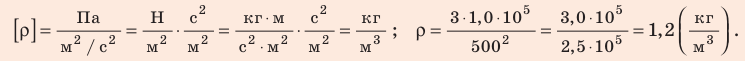
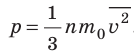 . Это уравнение можно записать в виде:
. Это уравнение можно записать в виде: 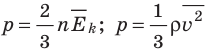 .
.