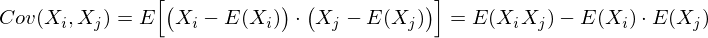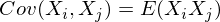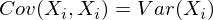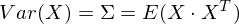В этой статье я бы хотел рассказать о том, как именно работает метод анализа главных компонент (PCA – principal component analysis) с точки зрения интуиции, стоящей за ее математическим аппаратом. Максимально просто, но подробно.
Математика вообще очень красивая и изящная наука, но порой ее красота скрывается за кучей слоев абстракции. Показать эту красоту лучше всего на простых примерах, которые, так сказать, можно покрутить, поиграть и пощупать, потому что в конце концов все оказывается гораздо проще, чем кажется на первый взгляд – самое главное понять и представить.
В анализе данных, как и в любом другом анализе, порой бывает нелишним создать упрощенную модель, максимально точно описывающую реальное положение дел. Часто бывает так, что признаки довольно сильно зависят друг от друга и их одновременное наличие избыточно.
К примеру, расход топлива у нас меряется в литрах на 100 км, а в США в милях на галлон. На первый взгляд, величины разные, но на самом деле они строго зависят друг от друга. В миле 1600м, а в галлоне 3.8л. Один признак строго зависит от другого, зная один, знаем и другой.
Но гораздо чаще бывает так, что признаки зависят друг от друга не так строго и (что важно!) не так явно. Объем двигателя в целом положительно влияет на разгон до 100 км/ч, но это верно не всегда. А еще может оказаться, что с учетом не видимых на первый взгляд факторов (типа улучшения качества топлива, использования более легких материалов и прочих современных достижений), год автомобиля не сильно, но тоже влияет на его разгон.
Зная зависимости и их силу, мы можем выразить несколько признаков через один, слить воедино, так сказать, и работать уже с более простой моделью. Конечно, избежать потерь информации, скорее всего не удастся, но минимизировать ее нам поможет как раз метод PCA.
Выражаясь более строго, данный метод аппроксимирует n-размерное облако наблюдений до эллипсоида (тоже n-мерного), полуоси которого и будут являться будущими главными компонентами. И при проекции на такие оси (снижении размерности) сохраняется наибольшее количество информации.
- Шаг 1. Подготовка данных
- Шаг 2. Ковариационная матрица
- Шаг 3. Собственные вектора и значения (айгенпары)
- Шаг 4. Снижение размерности (проекция)
- Шаг 5. Восстановление данных
- Вместо заключения – проверка алгоритма
- Содержание
- 1. Базовые сведения
- 1.1. Данные
- 1.2. Интуитивный подход
- 1.3. Понижение размерности
- 2. Метод главных компонент
- 2.1. Формальное описание
- 2.2. Алгоритм
- 2.3. PCA и SVD
- 2.4. Счета
- 2.5. Нагрузки
- 2.6. Данные специального вида
- 2.7. Погрешности
- 2.8. Проверка
- 2.9. «Качество» декомпозиции
- 2.10. Выбор числа главных компонент
- 2.11. Неединственность PCA
- 2.12. Подготовка данных
- 2.1 3 . Размах и отклонение
- 3. Люди и страны
- 3.1. Пример
- 3.2. Данные
- 3.3. Исследование данных
- 3.4. Подготовка данных
- 3.5. Вычисление счетов и нагрузок
- 3.6. Графики счетов
- 3.7. Графики нагрузок
- 3.8. Исследование остатков
- Заключение
- Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы (продолжение)
- 2. Методы, основанные на критерии автоинформативности системы признаков
- Метод главных компонент
- Факторный анализ
- Метод контрастных групп
Шаг 1. Подготовка данных
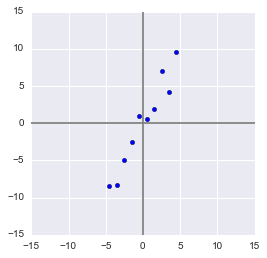
Здесь для простоты примера я не буду брать реальные обучающие датасеты на десятки признаков и сотни наблюдений, а сделаю свой, максимально простой игрушечный пример. 2 признака и 10 наблюдений будет вполне достаточно для описания того, что, а главное – зачем, происходит в недрах алгоритма.
В данной выборке у нас имеются два признака, сильно коррелирующие друг с другом. С помощью алгоритма PCA мы сможем легко найти признак-комбинацию и, ценой части информации, выразить оба этих признака одним новым. Итак, давайте разбираться!
Для начала немного статистики. Вспомним, что для описания случайной величины используются моменты. Нужные нам – мат. ожидание и дисперсия. Можно сказать, что мат. ожидание – это «центр тяжести» величины, а дисперсия – это ее «размеры». Грубо говоря, мат. ожидание задает положение случайной величины, а дисперсия – ее размер (точнее, разброс).
Сам процесс проецирования на вектор никак не влияет на значения средних, так как для минимизации потерь информации наш вектор должен проходить через центр нашей выборки. Поэтому нет ничего страшного, если мы отцентрируем нашу выборку – линейно сдвинем ее так, чтобы средние значения признаков были равны 0. Это очень сильно упростит наши дальнейшие вычисления (хотя, стоит отметить, что можно обойтись и без центрирования).
Оператор, обратный сдвигу будет равен вектору изначальных средних значений – он понадобится для восстановления выборки в исходной размерности.
Дисперсия же сильно зависит от порядков значений случайной величины, т.е. чувствительна к масштабированию. Поэтому если единицы измерения признаков сильно различаются своими порядками, крайне рекомендуется стандартизировать их. В нашем случае значения не сильно разнятся в порядках, так что для простоты примера мы не будем выполнять эту операцию.
Шаг 2. Ковариационная матрица
В случае с многомерной случайной величиной (случайным вектором) положение центра все так же будет являться мат. ожиданиями ее проекций на оси. А вот для описания ее формы уже недостаточно толькое ее дисперсий по осям. Посмотрите на эти графики, у всех трех случайных величин одинаковые мат.ожидания и дисперсии, а их проекции на оси в целом окажутся одинаковы!
Для описания формы случайного вектора необходима ковариационная матрица.
Это матрица, у которой (i,j)-элемент является корреляцией признаков (Xi, Xj). Вспомним формулу ковариации:
В нашем случае она упрощается, так как
и это справедливо для любых случайных величин.
Таким образом, в нашей матрице по диагонали будут дисперсии признаков (т.к. i = j), а в остальных ячейках – ковариации соответствующих пар признаков. А в силу симметричности ковариации матрица тоже будет симметрична.
Замечание: Ковариационная матрица является обобщением дисперсии на случай многомерных случайных величин – она так же описывает форму (разброс) случайной величины, как и дисперсия.
И действительно, дисперсия одномерной случайной величины – это ковариационная матрица размера 1×1, в которой ее единственный член задан формулой Cov(X,X) = Var(X).
Итак, сформируем ковариационную матрицу Σ для нашей выборки. Для этого посчитаем дисперсии Xi и Xj, а также их ковариацию. Можно воспользоваться вышенаписанной формулой, но раз уж мы вооружились Python’ом, то грех не воспользоваться функцией numpy.cov(X). Она принимает на вход список всех признаков случайной величины и возвращает ее ковариационную матрицу и где X – n-мерный случайный вектор (n-количество строк). Функция отлично подходит и для расчета несмещенной дисперсии, и для ковариации двух величин, и для составления ковариационной матрицы.
(Напомню, что в Python матрица представляется массивом-столбцом массивов-строк.)
Шаг 3. Собственные вектора и значения (айгенпары)
О’кей, мы получили матрицу, описывающую форму нашей случайной величины, из которой мы можем получить ее размеры по x и y (т.е. X1 и X2), а также примерную форму на плоскости. Теперь надо найти такой вектор (в нашем случае только один), при котором максимизировался бы размер (дисперсия) проекции нашей выборки на него.
Замечание: Обобщение дисперсии на высшие размерности — ковариационная матрица, и эти два понятия эквивалентны. При проекции на вектор максимизируется дисперсия проекции, при проекции на пространства больших порядков – вся ее ковариационная матрица.
Итак, возьмем единичный вектор на который будем проецировать наш случайный вектор X. Тогда проекция на него будет равна v T X. Дисперсия проекции на вектор будет соответственно равна Var(v T X). В общем виде в векторной форме (для центрированных величин) дисперсия выражается так:
Соответственно, дисперсия проекции:
Легко заметить, что дисперсия максимизируется при максимальном значении v T Σv. Здесь нам поможет отношение Рэлея. Не вдаваясь слишком глубоко в математику, просто скажу, что у отношения Рэлея есть специальный случай для ковариационных матриц:
Последняя формула должна быть знакома по теме разложения матрицы на собственные вектора и значения. x является собственным вектором, а λ – собственным значением. Количество собственных векторов и значений равны размеру матрицы (и значения могут повторяться).
Кстати, в английском языке собственные значения и векторы именуются eigenvalues и eigenvectors соответственно.
Мне кажется, это звучит намного более красиво (и кратко), чем наши термины.
Таким образом, направление максимальной дисперсии у проекции всегда совпадает с айгенвектором, имеющим максимальное собственное значение, равное величине этой дисперсии.
И это справедливо также для проекций на большее количество измерений – дисперсия (ковариационная матрица) проекции на m-мерное пространство будет максимальна в направлении m айгенвекторов, имеющих максимальные собственные значения.
Размерность нашей выборки равна двум и количество айгенвекторов у нее, соответственно, 2. Найдем их.
В библиотеке numpy реализована функция numpy.linalg.eig(X), где X – квадратная матрица. Она возвращает 2 массива – массив айгензначений и массив айгенвекторов (векторы-столбцы). И векторы нормированы — их длина равна 1. Как раз то, что надо. Эти 2 вектора задают новый базис для выборки, такой что его оси совпадают с полуосями аппроксимирующего эллипса нашей выборки.
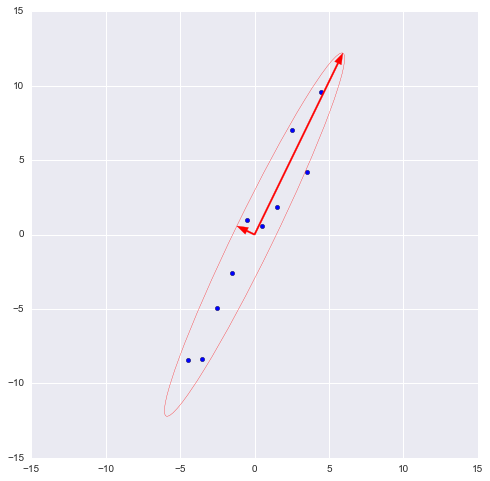
На этом графике мы апроксимировали нашу выборку эллипсом с радиусами в 2 сигмы (т.е. он должен содержать в себе 95% всех наблюдений – что в принципе мы здесь и наблюдаем). Я инвертировал больший вектор (функция eig(X) направляла его в обратную сторону) – нам важно направление, а не ориентация вектора.
Шаг 4. Снижение размерности (проекция)
Наибольший вектор имеет направление, схожее с линией регрессии и, спроецировав на него нашу выборку, мы потеряем информацию, сравнимую с суммой остаточных членов регрессии (только расстояние теперь евклидово, а не дельта по Y). В нашем случае зависимость между признаками очень сильная, так что потеря информации будет минимальна. «Цена» проекции — дисперсия по меньшему айгенвектору — как видно из предыдущего графика, очень невелика.
Замечание: диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому (по главным компонентам).
Часто требуется оценить объем потерянной (и сохраненной) информации. Удобнее всего представить в процентах. Мы берем дисперсии по каждой из осей и делим на общую сумму дисперсий по осям (т.е. сумму всех собственных чисел ковариационной матрицы).
Таким образом, наш больший вектор описывает 45.994 / 46.431 * 100% = 99.06%, а меньший, соответственно, примерно 0.94%. Отбросив меньший вектор и спроецировав данные на больший, мы потеряем меньше 1% информации! Отличный результат!
Замечание: На практике, в большинстве случаев, если суммарная потеря информации составляет не более 10-20%, то можно спокойно снижать размерность.
Для проведения проекции, как уже упоминалось ранее на шаге 3, надо провести операцию v T X (вектор должен быть длины 1). Или, если у нас не один вектор, а гиперплоскость, то вместо вектора v T берем матрицу базисных векторов V T . Полученный вектор (или матрица) будет являться массивом проекций наших наблюдений.
dot(X,Y) — почленное произведение (так мы перемножаем векторы и матрицы в Python)
Нетрудно заметить, что значения проекций соответствуют картине на предыдущем графике.
Шаг 5. Восстановление данных
С проекцией удобно работать, строить на ее основе гипотезы и разрабатывать модели. Но не всегда полученные главные компоненты будут иметь явный, понятный постороннему человеку, смысл. Иногда полезно раскодировать, к примеру, обнаруженные выбросы, чтобы посмотреть, что за наблюдения за ними стоят.
Это очень просто. У нас есть вся необходимая информация, а именно координаты базисных векторов в исходном базисе (векторы, на которые мы проецировали) и вектор средних (для отмены центровки). Возьмем, к примеру, наибольшее значение: 10.596… и раскодируем его. Для этого умножим его справа на транспонированный вектор и прибавим вектор средних, или в общем виде для всей выборки: X T v T +m
Разница небольшая, но она есть. Ведь потерянная информация не восстанавливается. Тем не менее, если простота важнее точности, восстановленное значение отлично аппроксимирует исходное.
Вместо заключения – проверка алгоритма
Итак, мы разобрали алгоритм, показали как он работает на игрушечном примере, теперь осталось только сравнить его с PCA, реализованным в sklearn – ведь пользоваться будем именно им.
Параметр n_components указывает на количество измерений, на которые будет производиться проекция, то есть до скольки измерений мы хотим снизить наш датасет. Другими словами – это n айгенвекторов с самыми большими собственными числами. Проверим результат снижения размерности:
Мы возвращали результат как матрицу вектор-столбцов наблюдений (это более канонический вид с точки зрения линейной алгебры), PCA в sklearn же возвращает вертикальный массив.
В принципе, это не критично, просто стоит отметить, что в линейной алгебре канонично записывать матрицы через вектор-столбцы, а в анализе данных (и прочих связанных с БД областях) наблюдения (транзакции, записи) обычно записываются строками.
Проверим и прочие параметры модели – функция имеет ряд атрибутов, позволяющих получить доступ к промежуточным переменным:
— Вектор средних: mean_
— Вектор(матрица) проекции: components_
— Дисперсии осей проекции (выборочная): explained_variance_
— Доля информации (доля от общей дисперсии): explained_variance_ratio_
Замечание: explained_variance_ показывает выборочную дисперсию, тогда как функция cov() для построения ковариационной матрицы рассчитывает несмещенные дисперсии!
Сравним полученные нами значения со значениями библиотечной функции.
Единственное различие – в дисперсиях, но как уже упоминалось, мы использовали функцию cov(), которая использует несмещенную дисперсию, тогда как атрибут explained_variance_ возвращает выборочную. Они отличаются только тем, что первая для получения мат.ожидания делит на (n-1), а вторая – на n. Легко проверить, что 45.99 ∙ (10 — 1) / 10 = 41.39.
Все остальные значения совпадают, что означает, что наши алгоритмы эквивалентны. И напоследок замечу, что атрибуты библиотечного алгоритма имеют меньшую точность, поскольку он наверняка оптимизирован под быстродействие, либо просто для удобства округляет значения (либо у меня какие-то глюки).
Замечание: библиотечный метод автоматически проецирует на оси, максимизирующие дисперсию. Это не всегда рационально. К примеру, на данном рисунке неаккуратное снижение размерности приведет к тому, что классификация станет невозможна. Тем не менее, проекция на меньший вектор успешно снизит размерность и сохранит классификатор.
Итак, мы рассмотрели принципы работы алгоритма PCA и его реализации в sklearn. Я надеюсь, эта статья была достаточно понятна тем, кто только начинает знакомство с анализом данных, а также хоть немного информативна для тех, кто хорошо знает данный алгоритм. Интуитивное представление крайне полезно для понимания того, как работает метод, а понимание очень важно для правильной настройки выбранной модели. Спасибо за внимание!
Видео:Идея и суть метода главных компонентСкачать

Содержание
В этом пособии рассказывается о методе главных компонент (Principal Component Analysis, PCA) – базовом подходе, применяемом в хемометрике для решения разнообразных задач. Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить изучение вопроса можно с помощью указанной Литературы
В пособии интенсивно используются понятия и методы матричной алгебры – вектор, матрица, и т.п. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, пособие «Матрицы и векторы».
Изложение иллюстрируется примерами, выполненными в рабочей книге Excel «People.xls» которая сопровождает этот документ . Эта книга может работать без использования Chemometrics Add-In.
Ссылки на примеры помещены в текст как объекты Excel. По форме, эти примеры имеют абстрактный, модельный характер, однако, по сути, они тесно связаны с задачами, встречающимися на практике. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как MMULT , TREND . Освежить эти знания можно с помощью пособия Матричные операции в Excel.
Видео:#25. Метод главных компонент (Principal Component Analysis) | Машинное обучениеСкачать

1. Базовые сведения
Видео:Метод главных компонент (PCA)Скачать

1.1. Данные
Метод главных компонент применяется к данным, записанным в виде матрицы X – прямоугольной таблицы чисел размерностью I строк и J столбцов.
Рис. 1 Матрица данных
Традиционно строки этой матрицы называются образцами. Они нумеруются индексом i, меняющимся от 1 до I. Столбцы называются переменными, и они нумеруются индексом j= 1, …, J.
Цель PCA – извлечение из этих данных нужной информации. Что является информацией, зависит от сути решаемой задачи. Данные могут содержать нужную нам информацию, они даже могут быть избыточными. Однако, в некоторых случаях, информации в данных может не быть совсем.
Размерность данных – число образцов и переменных – имеет большое значение для успешной добычи информации. Лишних данных не бывает – лучше, когда их много, чем мало. На практике это означает, что если получен спектр какого–то образца, то не нужно выбрасывать все точки, кроме нескольких характерных длин волн, а использовать их все, или, по крайней мере, значительный кусок.
Данные всегда (или почти всегда) содержат в себе нежелательную составляющую, называемую шумом. Природа этого шума может быть различной, но, во многих случаях, шум – это та часть данных, которая не содержит искомой информации. Что считать шумом, а что – информацией, всегда решается с учетом поставленных целей и методов, используемых для ее достижения.
Шум и избыточность в данных обязательно проявляют себя через корреляционные связи между переменными. Погрешности в данных могут привести к появлению не систематических, а случайных связей между переменными. Понятие эффективного (химического) ранга и скрытых, латентных переменных, число которых равно этому рангу, является важнейшим понятием в PCA
Видео:Простой пример нахождения главных компонентСкачать

1.2. Интуитивный подход
Постараемся передать суть метода главных компонент, используя интуитивно–понятную геометрическую интерпретацию. Начнем с простейшего случая, когда имеются только две переменные x1 и x2. Такие данные легко изобразить на плоскости (Рис. 2).
Рис. 2 Графическое представление двумерных данных
Каждой строке исходной таблицы (т.е. образцу) соответствует точка на плоскости с соответствующими координатами. Они обозначены пустыми кружками на Рис. 2. Проведем через них прямую, так, чтобы вдоль нее происходило максимальное изменение данных. На рисунке эта прямая выделена синим цветом; она называется первой главной компонентой – PC1. Затем спроецируем все исходные точки на эту ось. Получившиеся точки закрашены красным цветом. Теперь мы можем предположить, что на самом деле все наши экспериментальные точки и должны были лежать на этой новой оси. Просто какие–то неведомые силы отклонили их от правильного, идеального положения, а мы вернули их на место. Тогда все отклонения от новой оси можно считать шумом, т.е. ненужной нам информацией. Правда, мы должны быть в этом уверены. Проверить шум ли это, или все еще важная часть данных, можно поступив с этими остатками так же, как мы поступили с исходными данными – найти в них ось максимальных изменений. Она называется второй главной компонентой (PC2). И так надо действовать, до тех пор, пока шум уже не станет действительно шумом, т.е. случайным хаотическим набором величин.
В общем, многомерном случае, процесс выделения главных компонент происходит так:
- Ищется центр облака данных, и туда переносится новое начало координат – это нулевая главная компонента (PC0)
- Выбирается направление максимального изменения данных – это первая главная компонента (PC1)
- Если данные описаны не полностью (шум велик), то выбирается еще одно направление (PC2) – перпендикулярное к первому, так чтобы описать оставшееся изменение в данных и т.д.

Рис. 3 Графическое представление метода главных компонент
В результате, мы переходим от большого количества переменных к новому представлению, размерность которого значительно меньше. Часто удается упростить данные на порядки: от 1000 переменных перейти всего к двум. При этом ничего не выбрасывается – все переменные учитываются. В то же время несущественная для сути дела часть данных отделяется, превращается в шум. Найденные главные компоненты и дают нам искомые скрытые переменные, управляющие устройством данных.
Видео:A.7.37 Метод главных компонент (PCA) | линейная алгебра + теория вероятностей = анализ данныхСкачать

1.3. Понижение размерности
Суть метода главных компонент – это существенное понижение размерности данных. Исходная матрица X заменяется двумя новыми матрицами T и P, размерность которых, A, меньше, чем число переменных (столбцов) J у исходной матрицы X
Рис. 4 Декомпозиция матрицы X
Вторая размерность – число образцов (строк) I сохраняется. Если декомпозиция выполнена правильно – размерность A выбрана верно, то матрица T несет в себе столько же информации, сколько ее было в начале, в матрице X. При этом матрица T меньше, и, стало быть, проще, чем X.
Видео:Метод главных компонент в R (principal component analysis)Скачать

2. Метод главных компонент
Видео:PCA METHOD. ПРИНЦИП ГЛАВНЫХ КОМПОНЕНТСкачать

2.1. Формальное описание
Пусть имеется матрица переменных X размерностью (I × J), где I – число образцов (строк), а J – это число независимых переменных (столбцов), которых, как правило, много (J>>1). В методе главных компонент используются новые, формальные переменные ta (a=1,…A), являющиеся линейной комбинацией исходных переменных xj (j=1,…J)
ta=pa1x1+… + paJxJ
С помощью этих новых переменных матрица X разлагается в произведение двух матриц T и P –
Матрица T называется матрицей счетов (scores). Ее размерность (I × A).
Матрица P называется матрицей нагрузок (loadings). Ее размерность (J × A ).
E – это матрица остатков, размерностью (I × J).
Рис. 5 Разложение по главным компонентам
Новые переменные ta называются главными компонентами (Principal Components), поэтому и сам метод называется методом главных компонент (PCA). Число столбцов – ta в матрице T, и pa в матрице P, равно A, которое называется числом главных компонент (PC). Эта величина заведомо меньше числа переменных J и числа образцов I.
Важным свойством PCA является ортогональность (независимость) главных компонент. Поэтому матрица счетов T не перестраивается при увеличении числа компонент, а к ней просто прибавляется еще один столбец – соответствующий новому направлению. Тоже происходит и с матрицей нагрузок P.
Видео:Свойства главных компонентСкачать

2.2. Алгоритм
Чаще всего для построения PCA счетов и нагрузок, используется рекуррентный алгоритм NIPALS, который на каждом шагу вычисляет одну компоненту. Сначала исходная матрица X преобразуется (как минимум – центрируется; см. раздел 2.12) и превращается в матрицу E0, a=0. Далее применяют следующий алгоритм.
После вычисления очередной (a-ой) компоненты, полагаем ta=t и pa=p. Для получения следующей компоненты надо вычислить остатки Ea+1 = Ea – t p t и применить к ним тот же алгоритм, заменив индекс a на a+1. Программа для реализации PCA в среде MatLab приведена в пособии MatLab. Руководство для начинающих .
В этом пособии для построения PCA используется специальная надстройка для программы Excel (Add–In) Chemometrics.xla. Она дополняет список стандартных функций Excel и позволяет проводить PCA разложение на листах рабочей книги. Подробности об этой программе можно прочитать в пособии Проекционные методы в системе Excel.
После того, как построено пространство из главных компонент, новые образцы Xnew могут быть на него спроецированы, иными словами – определены матрицы их счетов Tnew. В методе PCA это делается очень просто
Tnew.=. Xnew P
Видео:15. МО-1 ФКН: метод главных компонентСкачать

2.3. PCA и SVD
Метод главных компонент тесно связан с другим разложением – по сингулярным значениям, SVD. В последнем случае исходная матрица X разлагается в произведение трех матриц
Здесь U – матрица, образованная ортонормированными собственными векторами ur матрицы XX t , соответствующим значениям λr;
V– матрица, образованная ортонормированными собственными векторами vr матрицы X t X;
S – положительно определенная диагональная матрица, элементами которой являются сингулярные значения σ 1 ≥. ≥σ R ≥0 равные квадратным корням из собственных значений λr
Связь между PCA и SVD определяется следующими простыми соотношениями
Видео:009. Регрессионный анализ и метод главных компонентов - К. В. ВоронцовСкачать

2.4. Счета
Матрица счетов T дает нам проекции исходных образцов (J –мерных векторов x1,…,xI) на подпространство главных компонент (A-мерное). Строки t1,…,tI матрицы T – это координаты образцов в новой системе координат. Столбцы t1,…,tA матрицы T – ортогональны и представляют проекции всех образцов на одну новую координатную ось.
При исследовании данных методом PCA, особое внимание уделяется графикам счетов. Они несут в себе информацию, полезную для понимания того, как устроены данные. На графике счетов каждый образец изображается в координатах (ti, tj), чаще всего – (t1, t2), обозначаемых PC1 и PC2. Близость двух точек означает их схожесть, т.е. положительную корреляцию. Точки, расположенные под прямым углом, являются некоррелироваными, а расположенные диаметрально противоположно – имеют отрицательную корреляцию.
Рис.6 График счетов
Подробнее о том, как из графиков счетов извлекается полезная информация, будет рассказано в примере.
Для матрицы счетов имеют место следующие соотношения –
где величины λ 1 ≥. ≥λ A ≥0 – это собственные значения. Они характеризуют важность каждой компоненты
Нулевое собственное значение λ0 определяется как сумма всех собственных значений, т.е.
Для вычисления PCA- счетов в надстройке Chemometrics Add-In используется функция ScoresPCA .
Видео:Подбор оптимальной предварительной обработки данных для метода главных компонент - PCAСкачать

2.5. Нагрузки
Матрица нагрузок P – это матрица перехода из исходного пространства переменных x1, …xJ (J-мерного) в пространство главных компонент (A-мерное). Каждая строка матрицы P состоит из коэффициентов, связывающих переменные t и x (1). Например, a-я строка – это проекция всех переменных x1, …xJ на a-ю ось главных компонент. Каждый столбец P – это проекция соответствующей переменной xj на новую систему координат.
Рис.7 График нагрузок
График нагрузок применяется для исследования роли переменных. На этом графике каждая переменная xj отображается точкой в координатах (pi, pj), например (p1, p2). Анализируя его аналогично графику счетов, можно понять, какие переменные связаны, а какие независимы. Совместное исследование парных графиков счетов и нагрузок, также может дать много полезной информации о данных.
В методе главных компонент нагрузки – это ортогональные нормированные вектора, т.е.
Для вычисления PCA- нагрузок в надстройке Chemometrics Add-In используется функция Loadings PCA .
Видео:Метод главных компонент(Principal component analysis) часть 1Скачать

2.6. Данные специального вида
Результат моделирования методом главных компонент не зависит от порядка, в котором следуют образцы и/или переменные. Иными словами строки и столбцы в исходной матрице X можно переставить, но ничего принципиально не изменится. Однако, в некоторых случаях, сохранять и отслеживать этот порядок очень полезно – это позволяет лучше понять устройство моделируемых данных.
Рис. 8 Данные ВЭЖХ–ДДМ
Рассмотрим простой пример – моделирование данных, полученных методом высокоэффективной жидкостной хроматографией с детектированием на диодной матрице (ВЭЖХ–ДДМ). Данные представляются матрицей, размерностью 30 образцов (I) на 28 переменных (J). Образцы соответствуют временам удерживания от 0 до 30 с, а переменные – длинам волн от 220 до 350 нм, на которых происходит детектирование. Данные ВЭЖХ–ДДМ представлены на Рис 8.
Эти данные хорошо моделируются методом PCA с двумя главными компонентами. Ясно, что в этом примере нам важен порядок, в котором идут образцы и переменные – он задается естественным ходом времени и спектральным диапазоном. Полученные счета и нагрузки полезно изобразить на графиках в зависимости от соответствующего параметра – счета от времени, а нагрузки от длины волны. (см. Рис 9)
Рис. 9 Графики счетов и нагрузок для данных ВЭЖХ–ДДМ
Подробнее этот пример разобран в пособии Разрешение многомерных кривых .
Видео:Метод главных компонент - практика на PythonСкачать

2.7. Погрешности
PCA декомпозиция матрицы X является последовательным, итеративным процессом, который можно оборвать на любом шаге a=A. Получившаяся матрица
вообще говоря, отличается от матрицы X. Разница между ними
называется матрицей остатков.
Рассмотрим геометрическую интерпретацию остатков. Каждый исходный образец xi (строка в матрице X) можно представить как вектор в J– мерном пространстве с координатами
Рис. 10 Геометрия PCA
PCA проецирует его в вектор, лежащий в пространстве главных компонент, ti=(ti1, ti2, …tiA) размерностью A. В исходном пространстве этот же вектор ti имеет координаты
Разница между исходным вектором и его проекцией является вектором остатков
Он образует i–ю строку в матрице остатков E.
Рис.11 Вычисление остатков
Исследуя остатки можно понять, как устроены данные и хорошо ли они описываются PCA моделью.
Для вычисления PCA- остатков можно использовать приемы, описанные в пособии Расширение возможностей Chemometrics Add-In.
определяет квадрат отклонения исходного вектора xi от его проекции на пространство PC. Чем оно меньше, тем лучше приближается i–ый образец.
Эта же величина, деленная на число переменных
Среднее (для всех образцов) расстояние v0 вычисляется как
Оценка общая (для всех образцов) дисперсии вычисляется так –
Видео:Mашинное Oбучение -метод опорных векторов -метод главных компонентСкачать

2.8. Проверка
В случае, когда PCA модель предназначена для предсказания или для классификации, а не для простого исследования данных, такая модель нуждается в подтверждении (валидации). При проверке методом тест–валидации исходный массив данных состоит из двух независимо полученных наборов, каждый из которых является достаточно представительным. Первый набор, называемый обучающим, используется для моделирования. Второй набор, называемый проверочным, служит только для проверки модели. Построенная модель применяется к данным из проверочного набора, и полученные результаты сравниваются с проверочными значениями. Таким образом принимается решение о правильности, точности моделирования.
Рис.12 Обучающий и проверочный наборы
В некоторых случаях объем данных слишком мал для такой проверки. Тогда применяют другой метод – перекрестной проверки (кросс–валидация), о котором можно прочитать здесь.
Используется также проверка методом коррекции размахом, суть которой предлагается изучить самостоятельно.
Видео:Лекция 9. Факторный анализ и метод главных компонент, продолжениеСкачать

2.9. «Качество» декомпозиции
Результатом PCA моделирования являются величины 



Следующие величины характеризуют «качество» моделирования в среднем.
Полная дисперсия остатков в обучении (TRVC) и в проверке (TRVP) –
Полная дисперсия выражается в тех же единицах (точнее их квадратах), что и исходные величины X.
Объясненная дисперсия остатков в обучении (ERVC) и в проверке (ERVP)
Объясненная дисперсия – это относительная величина. При ее вычислении используется естественная нормировка – сумма квадратов всех исходных величин xij. Обычно она выражается в процентах или в долях единицы. Во всех этих формулах величины eij – это элементы матриц Ec или Et. Для характеристик, наименование которых оканчивается на C (например, TRVC), используется матрица Ec (обучение), а для тех, которые оканчиваются на P (например, TRVP), берется матрица Et (проверка).
Видео:principle component analysis Анализ главных компонент NIPALSСкачать

2.10. Выбор числа главных компонент
Как уже отмечалось выше, метод главных компонент – это итерационная процедура, в которой новые компоненты добавляются последовательно, одна за другой. Важно знать, когда остановить этот процесс, т.е. как определить правильное число главных компонент, A. Если это число слишком мало, то описание данных будет не полным. С другой стороны, избыточное число главных компонент приводит к переоценке, т.е. к ситуации, когда моделируется шум, а не содержательная информация.
Для выбора значения числа главных компонент обычно используется график, на котором объясненная дисперсия (ERV) изображается в зависимости от числа PC. Пример такого графика приведен на Рис. 13.
Рис. 13 Выбор числа PC
Из этого графика видно, что правильное число PC – это 3 или 4. Три компоненты объясняют 95%, а четыре 98% исходной вариации. Окончательное решение о величине A можно принять только после содержательного анализа данных.
Другим полезным инструментом является график, на котором изображаются собственные значения (4) в зависимости от числа PC. Пример показан на Рис.14.
Рис. 14 График собственных значений
Из этого рисунка опять видно, что для a=3 происходит резкое изменение формы графика – излом. Поэтому верное число PC – это три или четыре.
Видео:#26. Сокращение размерности признакового пространства с помощью PCA | Машинное обучениеСкачать

2.11. Неединственность PCA
Разложение по методу главных компонент
не является единственным. Вместо матриц T и P можно использовать другие матрицы 

с той же матрицей ошибок E. Простейший пример – это одновременное изменение знаков у соответствующих компонент векторов ta и pa, при котором произведение
остается неизменным. Алгоритм NIPALS дает именно такой результат – с точностью до знака, поэтому его реализация в разных программах может приводить к расхождениям в направлениях главных компонент.
Более сложный случай – это одновременное вращение матриц T и P. Пусть R – это ортогональная матрица вращения размерностью A × A , т.е такая матрица, что R t =R –1 . Тогда
Заметим, что новые матрицы счетов и нагрузок сохраняют все свойства старых,

Это свойство PCA называется вращательной неопределенностью. Оно интенсивно используется при решении задач разделения кривых, в частности методом прокрустова вращения. Если отказаться от условий ортогональности главных компонент, то декомпозиция матрицы станет еще более общей. Пусть теперь R – это произвольная невырожденная матрица размерностью A × A . Тогда
Эти матрицы счетов и нагрузок уже не удовлетворяют условию ортогональности и нормирования. Зато они могут состоять только из неотрицательных элементов, а также подчиняться другим требованиям, накладываемым при решении задач разделения сигналов.
Видео:Лекция 10. Факторный анализ и метод главных компонент. SVD разложениеСкачать

2.12. Подготовка данных
Во многих случаях, перед применением PCA, исходные данные нужно предварительно подготовить: отцентрировать и/или отнормировать. Эти преобразования проводятся по столбцам – переменным.
Центрирование – это вычитание из каждого столбца xj среднего (по столбцу) значения

Центрирование необходимо потому, что оригинальная PCA модель (2) не содержит свободного члена.
Второе простейшее преобразование данных – это нормирование. Это преобразование выравнивает вклад разных переменных в PCA модель. При этом преобразовании каждый столбец xj делится на свое стандартное отклонение.
Комбинация центрирования и нормирования по столбцам называется автошкалированием.
Любое преобразование данных – центрирование, нормирование, и т.п. – всегда делается сначала на обучающем наборе. По этому набору вычисляются значения mj и sj, которые затем применяются и к обучающему, и к проверочному набору.
В надстройке Chemometrics Add In подготовка данных проводится автоматически. Если подготовку нужно провести вручную, то для нее можно использовать стандартные функции листа или специальную пользовательскую функцию.
В задачах, где структура исходных данных X априори предполагает однородность и гомоскедастичность, подготовка данных не только не нужна, но и вредна. Именно такой случай представляют ВЭЖХ–ДДМ данные, рассмотренные в пособии Разрешение многомерных кривых.
Видео:Доленко С.А. - Машинное обучение в физике - 5. Анализ главных компонент и методы на его основеСкачать

2.1 3 . Размах и отклонение
При заданном числе главных компонент A, величина
называется размахом (leverage). Эта величина равна квадрату расстояния Махаланобиса от центра модели до i–го образца в пространстве счетов, поэтому размах характеризует как далеко находится каждый образец в гиперплоскости главных компонент.
Для размаха имеет место соотношение
которое выполняется тождественно – по построению PCA.
Другой важной характеристикой PCA модели является отклонение v i , которое вычисляется как сумма квадратов остатков (6) – квадрат эвклидова расстояния от плоскости главных компонент до объекта i.
Две эти величины: hi и vi определяют положение объекта (образца) относительно имеющейся PCA модели. Слишком большие значения размаха и/или отклонения свидетельствуют об особенности такого объекта, который может быть экстремальным или выпадающим образцом.
Анализ величин hi и vi составляет основу SIMCA – метода классификации с обучением.
3. Люди и страны
3.1. Пример
Метод главных компонент иллюстрируется примером, помещенным в файл People.xls.
Этот файл включает в себя следующие листы:
Layout: схемы, объясняющая имена массивов, используемых в примере
Data: данные, используемые в примере.
MVA: PCA декомпозиция, выполненная с помощью надстройки Chemometrics.xla
PCA: копия всех результатов PCA не привязанная к надстройке Chemometrics.xla
Scores1–2: анализ младших счетов PC1–PC2
Scores3–4: анализ старших счетов PC3–PC4
3.2. Данные
Анализ базируется на данных европейского демографического исследования, опубликованных в книге К. Эсбенсена.
По причинам дидактического характера используется лишь небольшой набор из 32 человек, из которых 16 представляют Северную Европу (Скандинавия) и столько же – Южную (Средиземноморье). Для баланса выбрано одинаковое количество мужчин и женщин – по 16 человек. Люди характеризуются двенадцатью переменными, перечисленными в Табл. 1.
Табл. 1 Переменные, использованные в демографическом анализе
| Height | Рост: в сантиметрах |
| Weight | Вес: в килограммах |
| Hair | Волосы: короткие: –1, или длинные: +1 |
| Shoes | Обувь: размер по европейскому стандарту |
| Age | Возраст: в годах |
| Income | Доход: в тысячах евро в год |
| Beer | Пиво: потребление в литрах в год |
| Wine | Вино: потребление в литрах в год |
| Sex | Пол: мужской: –1, или женский: +1 |
| Strength | Сила: индекс, основанный на проверке физических способностей |
| Region | Регион: север : –1, или юг: +1 |
| IQ | Коэффициент интеллекта, измеряемый по стандартному тесту |
Заметим, что такие переменные, как Sex, Hair и Region имеют дискретный характер с двумя возможными значениями: –1 или +1, тогда как остальные девять переменных могут принимать непрерывные числовые значения.
Рис. 15 Исходные данные в примере People
3.3. Исследование данных
Прежде всего, любопытно посмотреть на графиках, как связаны между собой все эти переменные. Зависит ли рост (Height ) от веса (Weight)? Отличаются ли женщины от мужчин в потреблении вина (Wine)? Связан ли доход (Income) с возрастом (Age)? Зависит ли вес (Weight) от потребления пива (Beer)?



Рис. 16 Связи между переменными в примере People.
Женщины (F) обозначены кружками ● и ● , а мужчины (M) – квадратами ■ и ■ .
Север (N) представлен голубым ■ , а юг (S) – красным цветом ● .
Некоторые из этих зависимостей показаны на Рис.16. Для наглядности на всех графиках использованы одни и те же обозначения: женщины (F) показаны кружками, мужчины (M) – квадратами, север (N) представлен голубым, а юг (S) – красным цветом.
Связь между весом (Weight) и ростом (Height) показана на Рис.16a. Очевидна, прямая (положительная) пропорциональность. Учитывая маркировку точек, можно заметить также, что мужчины (M) в большинстве своем тяжелее и выше женщин (F).
На Рис. 16b показана другая пара переменных: вес (Weight) и пиво (Beer). Здесь, помимо очевидных фактов, что большие люди пьют больше, а женщины – меньше, чем мужчины, можно заметить еще две отдельные группы – южан и северян. Первые пьют меньше пива при том же весе.
Эти же группы заметны и на Рис.16c, где показана зависимость между потреблением вина (Wine) и пива (Beer). Из него видно, что связь между этими переменными отрицательна – чем больше потребляется пива, тем меньше вина. На юге пьют больше вина, а на севере – пива. Интересно, что в обеих группах женщины располагаются слева, но не ниже по отношению к мужчинам. Это означает, что, потребляя меньше пива, прекрасный пол не уступает в вине.
Последний график на Рис. 16d показывает, как связаны возраст (Age) и доход (Income). Легко видеть, что даже в этом сравнительно небольшом наборе данных есть переменные, как с положительной, так и с отрицательной корреляцией.
Можно ли построить графики для всех пар переменных выборки? Вряд ли. Проблема состоит в том, что для 12 переменных существует 12(12–1)/2=66 таких комбинаций.
3.4. Подготовка данных
Перед тем, как подвергнуть данные анализу методом главных компонент, их надо подготовить. Простой статистический расчет показывает, что они нуждаются в автошкалировании (См. Рис. 17)
Рис. 17 Средние значения и СКО для переменных в примере People.
Средние значения по многим переменным отличаются от нуля. Кроме того, среднеквадратичные отклонения сильно разнятся. После автошкалирования среднее значение всех переменных становится равно нулю, а отклонение – единица.
Рис. 18 Автошкалированные данные в примере People.
В принципе, данные можно было бы не преобразовывать явно, на листе, а оставить как есть. Ведь стандартные хемометрические процедуры, собранные в программе Chemometrics могут центрировать и шкалировать данные при выполнении вычислений. Однако матрица автошкалированных данных понадобится нам при вычислении остатков в разделе 3.8 .
3.5. Вычисление счетов и нагрузок
Для построения PCA декомпозиции можно воспользоваться стандартными функциями ScoresPCA и LoadingsPCA, имеющимися в надстройке Chemometrics. Мы вычислим все 12 возможных главных компонент. В качестве первого аргумента используется исходный, не преобразованный массив данных, поэтому последний аргумент в обеих функциях равен 3 – автошкалирование.
Рис. 19 Вычисление матрицы счетов
Рис. 20 Вычисление матрицы нагрузок
В этом пособии все PCA вычисления проводятся в книге People.xls на листе MVA. Для удобства читателя эти же результаты продублированы на листе PCA как числа, без ссылки на надстройку Chemometrics.xla. Остальные листы рабочей книги связаны не с данными на листе MVA, с данными на листе PCA. Поэтому файл People.xls можно использовать даже тогда, когда надстройка Chemometrics.xla не установлена на компьютере.
3.6. Графики счетов
Посмотрим на графики счетов, которые показывают, как расположены образцы в проекционном пространстве.
На графике младших счетов PC1–PC2 (Рис. 21) мы видим четыре отдельные группы, разложенные по четырем квадрантам: слева – женщины (F), справа – мужчины (M), сверху – юг (S), а снизу – север (N). Из этого сразу становится ясен смысл первых двух направлений PC1 и PC2. Первая компонента разделяет людей по полу, а вторая – по месту жительства. Именно эти факторы наиболее сильно влияют на разброс свойств.
Рис. 21 График счетов (PC1 – PC2) с обозначениями, использованными ранее на Рис 16
Продолжим изучение, построив график старших счетов PC3– PC4 (Рис. 22 ).
Рис. 22 График счетов (PC3 – PC4) с новыми обозначениями:
размер и цвет символов отражает доход – чем больше и светлее, тем он больше. Числа представляют возраст
Здесь уже не видно таких отчетливых групп. Тем не менее, внимательно исследовав этот график совместно с таблицей исходных данных, можно, после некоторых усилий, сделать вывод о том, что PC3 отделяет старых/богатых людей от молодых/бедных. Чтобы сделать это более очевидным, мы изменили обозначения. Теперь каждый человек показан кружком, цвет и размер которого меняется в зависимости от дохода – чем больше и светлее, тем больше доход. Рядом показан возраст каждого объекта. Как видно, возраст и доход уменьшается слева направо, т.е. вдоль PC3. А вот смысл PC4 нам по–прежнему не ясен.
3.7. Графики нагрузок
Чтобы разобраться с этим, построим соответствующие графики нагрузок. Они подскажут нам, какие переменные и как связаны между собой, что влияет на что.
Из графика младших компонент мы сразу видим, что переменные рост (Height), вес (Weight), сила (Strength) и обувь (Shoes) образуют компактную группу в правой части графика. Они практически сливаются, что означает их тесную положительную корреляцию. Переменные волосы (Hair) и пол (Sex) находятся в другой группе, лежащей по диагонали от первой группы. Это свидетельствует о высокой отрицательной корреляции между переменными из этих групп, например, силой (Strength) и полом (Sex). Наибольшие нагрузки на вторую компоненту имеют переменные вино (Wine) и регион (Region), также тесно связанные друг с другом. Переменная доход (Income) лежит на первом графике напротив переменной регион (Region), что отражает дифференциацию состоятельности: Север–Юг. Можно заметить также и антитезу переменных пиво (Beer) –регион/вино(Region/Wine).

Рис. 23 Графики нагрузок: PC1 – PC2 и PC3 – PC4
Из второго графика мы видим большие нагрузки переменных возраст (Age) и доход (Income) на ось PC3, что соответствует графику счетов на Рис. 21. Рассмотрим, переменные пиво (Beer) и IQ. Первая из них имеет большие нагрузки как на PC1, так и на PC2, фактически формируя диагональ взаимоотношений между объектами на графике счетов. Переменная IQ не обнаруживает связи с другими переменным, так как ее значения близки к нулю для нагрузок первых трех PC, и проявляет она себя только в четвертой компоненте. Мы видим, что значения IQ не зависят от места жительства, физиологических характеристик и пристрастий к напиткам.
Впервые PCA был применен еще в начале 20–го века в психологических исследованиях, когда верили, что такие показатели, как IQ или криминальное поведение можно объяснить с помощью индивидуальных физиологических и социальных характеристик. Если сравнить результаты PCA с графиками, построенными нами ранее для пар переменных, видно, что PCA сразу дает всеобъемлющее представление о структуре данных, которое можно «охватить одним взглядом» (точнее, с помощью четырех графиков). Поэтому, одна из наиболее сильных сторон PCA в исследовании структур данных – это переход от большого числа не связанных между собой графиков пар переменных к очень небольшому числу графиков счетов и нагрузок.
3.8. Исследование остатков
Сколько главных компонент нужно использовать в этом примере? Для ответа на вопрос нужно исследовать, как изменяется качество описания при увеличении числа PC. Заметим, что в этом примере мы не будем проводить проверку – в этом нет необходимости, т.к. PCA модель нужна только для исследования данных. Она не будет использоваться далее для прогнозирования, классификации, и т.п.
Рис. 24 Графики собственных значений
На Рис.24 показано, как, в зависимости от числа PC, меняются собственные значения λ . Видно, что около PC=5 происходит изменение в их поведении. Для расчета показателей TRV и ERV можно получить матрицу остатков E для каждого числа главных компонент A и вычислить требуемые показатели. Пример такого расчета для значения A=4 приведен на листе Residuals.
Рис. 25 Анализ остатков
Однако те же характеристики можно получить и проще, если воспользоваться соотношениями
Эти величины представлены на Рис. 26
Рис. 26 Графики полной (TRV) и объясненной (ERV) дисперсии остатков
Из этих зависимостей видно, что для описания данных достаточно четырех PC – они моделируют 94% данных, или, иными словами, шум, оставшийся после проекции на четырехмерное пространство PC1–PC4, оставляет всего 6% от исходных данных.
Заключение
Рассмотренный пример позволил взглянуть лишь на малую часть возможностей, предоставляемых PCA–моделированием. Мы рассмотрели задачу исследования данных, которая не предполагает дальнейшего использования построенной модели для предсказания или классификации.
Метод PCA дает основу разнообразным методам, применяемым в хемометрике. В задачах классификации – это метод SIMCA, в задачах калибровки – это метод PCR, в задачах разделения кривых – это EFA, WFA и т.д.
Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы (продолжение)
Публикуется по материалам монографии В. А. Дюка
«Компьютерная психодиагностика», (С-Пб., 1994)
2. Методы, основанные на критерии автоинформативности системы признаков
Формальные алгоритмы рассматриваемой группы методов непосредственно не оперируют обучающей информацией о требуемом значении диагностируемой переменной. В то же время эта информация в неявном виде всегда присутствует в экспериментальных данных. Она закладывается на самом первом этапе конструирования психодиагностического теста, когда экспериментатор формирует исходное множество признаков, каждый из которых, по его мнению, должен отражать определенные аспекты тестируемого свойства. При этом под отражением данного свойства отдельным признаком, как правило, понимается самый простой вид связи признака с диагностируемым показателем — корреляция xi с у. Если тестируемое свойство гомогенно, то имеются все основания полагать, что мерой информативности для окончательного отбора признаков может служить степень согласованного действия этих признаков в нужном направлении.
Внутренняя согласованность заданий теста является важной категорией методов, опирающихся на критерий автоинформативности системы признаков. Согласованность измеряемых реакций испытуемых на тестовые стимулы означает то, что они должны иметь статистическую направленность на выражение общей, главной тенденции теста. Геометрическая структура экспериментальных данных, сформированных под влиянием кумулятивного эффекта согласованного взаимодействия признаков, в несколько идеализированном варианте выглядит как облако точек в пространстве признаков, вписывающееся в гиперэллипсоид. Все пары признаков при такой структуре имеют статистически значимые корреляции, а уравнение главной оси гиперэллипсоида — есть линейная диагностическая модель тестируемого свойства.
На приведенных представлениях базируются практически все методы построения психодиагностических тестов, опирающиеся на критерий автоинформативности системы признаков и использующие категорию внутренней согласованности заданий теста. Ниже будут рассмотрены основные методы этой группы.
Метод главных компонент
Метод главных компонент (МГК) был предложен Пирсоном в 1901 году и затем вновь открыт и детально разработан Хоттелингом /1933/. Ему посвящено большое количество исследований, и он широко представлен в литературных источниках, обратившись к которым можно получить сведения о методе главных компонент с различной степенью детализации и математической строгости (например, Айвазян С. А. и др., 1974, 1983, 1989). В данном разделе не ставится цель добиться подробного изложения всех особенностей МГК. Сконцентрируем свое внимание на основных феноменах метода главных компонент.
Метод главных компонент осуществляет переход к новой системе координат y1. ур в исходном пространстве признаков x1. xp которая является системой ортнормированных линейных комбинаций
где mi — математическое ожидание признака xi. Линейные комбинации выбираются таким образом, что среди всех возможных линейных нормированных комбинаций исходных признаков первая главная компонента у1(х) обладает наибольшей дисперсией. Геометрически это выглядит как ориентация новой координатной оси у1 вдоль направления наибольшей вытянутости эллипсоида рассеивания объектов исследуемой выборки в пространстве признаков x1. xp. Вторая главная компонента имеет наибольшую дисперсию среди всех оставшихся линейных преобразований, некоррелированных с первой главной компонентой. Она интерпретируется как направление наибольшей вытянутости эллипсоида рассеивания, перпендикулярное первой главной компоненте. Следующие главные компоненты определяются по аналогичной схеме.
Вычисление коэффициентов главных компонент wij основано на том факте, что векторы являются собственными (характеристическими) векторами корреляционной матрицы S. В свою очередь, соответствующие собственные числа этой матрицы равны дисперсиям проекций множества объектов на оси главных компонент.
Алгоритмы, обеспечивающие выполнение метода главных компонент, входят практически во все пакеты статистических программ.
Факторный анализ
В описанном выше методе главных компонент под критерием автоинформативности пространства признаков подразумевается, что ценную для диагностики информацию можно отразить в линейной модели, которая соответствует новой координатной оси в данном пространстве с максимальной дисперсией распределения проекций исследуемых объектов. Такой подход является продуктивным, когда явное большинство заданий «чернового» варианта теста согласованно «работает» на проявление тестируемого свойства и подавляет влияние иррелевантных факторов на распределение объектов. Также положительный результат будет получен при сравнительно небольшом объеме группы связанных информативных признаков, но при несогласованном взаимодействии посторонних факторов, под влиянием которых не нарушается однородность эллипсоида рассеивания, а лишь уменьшается вытянутость распределения объектов вдоль направления диагностируемой тенденции. В отличие от метода главных компонент факторный анализ основан не на дисперсионном критерии автоинформативности системы признаков, а ориентирован на объяснение имеющихся между признаками корреляций. Поэтому факторный анализ применяется в более сложных случаях совместного проявления на структуре экспериментальных данных тестируемого и иррелевантного свойств объектов, сопоставимых по степени внутренней согласованности, а также для выделения группы диагностических показателей из общего исходного множества признаков.
Основная модель факторного анализа записывается следующей системой равенств /Налимов В. В., 1971/
То есть полагается, что значения каждого признака xi могут быть выражены взвешенной суммой латентных переменных (простых факторов) fi, количество которых меньше числа исходных признаков, и остаточным членом εi с дисперсией σ 2 (εi), действующей только на xi, который называют специфическим фактором. Коэффициенты lij называются нагрузкой i-й переменной на j-й фактор или нагрузкой j-го фактора на i-ю переменную. В самой простой модели факторного анализа считается, что факторы fj взаимно независимы и их дисперсии равны единице, а случайные величины εi тоже независимы друг от друга и от какого-либо фактора fj. Максимально возможное количество факторов m при заданном числе признаков р определяется неравенством
(р+m) 2 ,
которое должно выполняться, чтобы задача не вырождалась в тривиальную. Данное неравенство получается на основании подсчета степеней свободы, имеющихся в задаче /Лоули Д. и др., 1967/. Сумму квадратов нагрузок в формуле основной модели факторного анализа называют общностью соответствующего признака xi и чем больше это значение, тем лучше описывается признак xi выделенными факторами fj. Общность есть часть дисперсии признака, которую объясняют факторы. В свою очередь, ε 2 i показывает, какая часть дисперсии исходного признака остается необъясненной при используемом наборе факторов и данную величину называют специфичностью признака. Таким образом,
Основное соотношение факторного анализа показывает, что коэффициент корреляции любых двух признаков xi и хj можно выразить суммой произведения нагрузок некоррелированных факторов
Задачу факторного анализа нельзя решить однозначно. Равенства основной модели факторного анализа не поддаются непосредственной проверке, так как р исходных признаков задается через (р+m) других переменных — простых и специфических факторов. Поэтому представление корреляционной матрицы факторами, как говорят, ее факторизацию, можно произвести бесконечно большим числом способов. Если удалось произвести факторизацию корреляционной матрицы с помощью некоторой матрицы факторных нагрузок F, то любое линейное ортогональное преобразование F (ортогональное вращение) приведет к такой же факторизации /Налимов В. В., 1971/.
Существующие программы вычисления нагрузок начинают работать с m =1 (однофакторная модель) /Александров В. В. и др., 1990/. Затем проверяется, насколько корреляционная матрица, восстановленная по однофакторной модели в соответствии с основным соотношением факторного анализа, отличается от корреляционной матрицы исходных данных. Если однофакторная модель признается неудовлетворительной, то испытывается модель с m=2 и т. д. до тех пор, пока при некотором m не будет достигнута адекватность или число факторов в модели не превысит максимально допустимое. В последнем случае говорят, что адекватной модели факторного анализа не существует. Если факторная модель существует, то производится вращение полученной системы общих факторов, так как значения факторных нагрузок и нагрузок на факторы есть лишь одно из возможных решений основной модели. Вращение факторов может производиться разными способами. Наиболее часто это вращение осуществляется таким образом, чтобы как можно большее число факторных нагрузок стало нулями и каждый фактор по возможности описывал группу сильно коррелированных признаков. Также можно вращать факторы до тех пор, пока не получатся результаты, поддающиеся содержательной интерпретации. Можно, например, потребовать, чтобы один фактор был нагружен преимущественно признаками одного типа, а другой — признаками другого типа. Или, скажем, можно потребовать, чтобы исчезли какие-то трудно интерпретируемые нагрузки с отрицательными знаками. Нередко исследователи идут дальше и рассматривают прямоугольную систему факторов как частный случай косоугольной, то есть ради содержания жертвуют условием некоррелированности факторов.
В завершение всей процедуры факторного анализа с помощью математических преобразований выражают факторы fj через исходные признаки, то есть получают в явном виде параметры линейной диагностической модели.
Известно большое количество методов факторного анализа (ротаций, максимального правдоподобия и др.). Нередко в одном и том же пакете программ анализа данных реализовано сразу несколько версий таких методов и у исследователей возникает правомерный вопрос о том, какой из них лучше. В этом вопросе наше мнение совпадает с /Александров В. В. и др., 1990/, где утверждается, что практически все методы дают весьма близкие результаты. Там же приводятся слова одного из основоположников современного факторного анализа Г. Хармана: «Ни в одной из работ не было показано, что какой-либо один метод приближается к «истинным» значениям общностей лучше, чем другие методы. Выбор среди группы методов «наилучшего» производится в основном с точки зрения вычислительных удобств, а также склонностей и привязанностей исследователя, которому тот или иной метод казался более адекватным его представлениям об общности» /Харман Г., 1972, с. 97/.
У факторного анализа есть много сторонников и много оппонентов. Но, как справедливо заметил В. В. Налимов: «. У психологов и социологов не оставалось других путей, и они изучили эти два приема (факторный анализ и метод главных компонент, — В. Д.) со всей обстоятельностью» /Налимов В. В., 1971, с. 100/. Для более подробного ознакомления с факторным анализом и его методами может быть рекомендована литература /Лоули Д., и др., 1967; Харман Г., 1972; Айвазян С. А. и др., 1974; Иберла К., 1980/.
Метод контрастных групп
Исходной информацией при использовании метода контрастных групп, помимо таблицы экспериментальных данных с результатами обследования испытуемых «черновым» вариантом психодиагностического теста, является также «черновая» версия линейного правила вычисления тестируемого показателя. Эта «черновая» версия может быть составлена экспериментатором, исходя из его теоретических представлений о том, какие признаки и с какими весами должны быть включены в линейную диагностическую модель. Кроме того, «черновая» версия может быть почерпнута из литературных источников, когда у экспериментатора возникает потребность адаптировать опубликованный психодиагностический тест к новым условиям. Метод контрастных групп применяется также в составе процедуры повышения внутренней согласованности заданий ранее отработанного теста.
В основе метода контрастных групп лежит гипотеза о том, что значительная часть «черновой» версии диагностической модели подобрана или угадана правильно. То есть в правую часть уравнения уч = уч(х) вошло достаточно много признаков, согласованно отражающих тестируемое свойство. В то же время в «черновой» версии уч(х) определенная доля признаков приходится на ненужный или даже вредный балласт, от которого нужно избавиться. Как и во всех других методах, опирающихся на категорию внутренней согласованности, это означает, что в пространстве признаков, включенных в исходную диагностическую модель, распределение объектов вписывается в эллипсоид рассеивания, вытянутый вдоль направления диагностируемой тенденции. В свою очередь, влияние информационного балласта выражается в уменьшении такой вытянутости эллипсоида рассеивания, так как «шумящие» признаки увеличивают разброс исследуемых объектов по всем другим направлениям. При этом «зашумление» основной тенденции будет тем сильнее, чем ближе к центру распределения располагаются диагностируемые объекты, и тем слабее, чем ближе к полюсам главной оси эллипсоида рассеивания находятся рассматриваемые объекты. Это связано с тем, что попадание объектов в крайние области объясняется, главным образом, кумулятивным эффектом согласованного взаимодействия информативных признаков. Описанные представления о структуре экспериментальных данных лежат в основе следующей процедуры, которая будет рассмотрена на примере анализа пунктов при конструировании тест-опросников /Шмелев А. Г., Похилько В. И., 1985/.
Сначала назначаются исходные шкальные ключи (веса) w˚j для пунктов теста (дихотомических признаков) хj. Для каждого i-го испытуемого подсчитывается суммарный тестовый балл
Обычно абсолютные значения весов wj определяют приблизительно и часто берут равными единице. Поэтому направление
будет несколько отличаться от направления главной диагонали эллипсоида рассеивания у(х) (рис. 3).
Рис. 3. Иллюстрация метода контрастных групп
Но если ориентировочно уч(х) правильно отражает диагностируемое свойство, то на краях распределения суммарного балла, построенного по всем объектам исследуемой выборки, можно выделить контрастные группы ω1 и ω2, в которые войдут объекты с минимальными погрешностями, вносимыми «шумящими» признаками. Эти группы не должны быть слишком малы. Для нормального распределения, как правило, берут контрастные группы объемом 27% от общего объема выборки, для более плоского — 33%. В принципе считается приемлемой любая цифра от 25 до 33% /Анастази А., 1982/. Следующий шаг заключается в определении степени связи каждого пункта с дихотомической переменной — номером контрастной группы. Мерой этой связи может служить так называемый коэффициент различения, представляющий собой разницу процентов того или иного ответа на анализируемый пункт в полярных группах испытуемых. Наиболее часто используется коэффициент связи Пирсона φ, который затем сравнивается с граничным значением
где χ 2 гр — стандартный квантиль распределения χ 2 с одной степенью свободы. Обычно ориентируются на 5% и 1% уровни значимости, для которых значение χ 2 равно 3,84 и 6,63 соответственно. Если для і-гo пункта |φі|