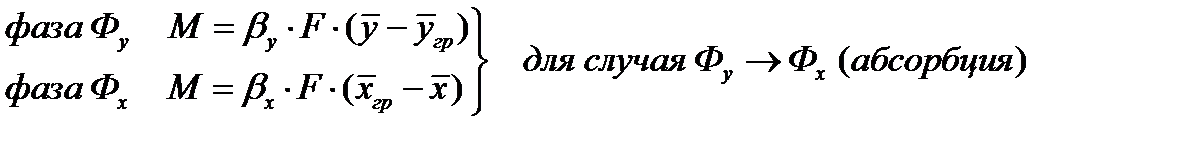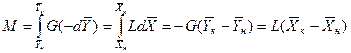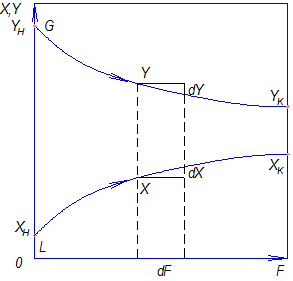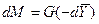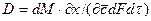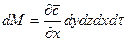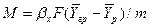Основное уравнение массопередачи коэффициенты массопередачи

12.1. ОБЩИЕ СВЕДЕНИЯ

Массопередача имеет место в процессах абсорбции, перегонки и ректификации, экстракции и выщелачивания, сушки, адсорбции, кристаллизации и др.

При абсорбции происходит селективное поглощение газов или паров жидкими поглотителями — абсорбентами, т. е. имеет место переход вещества из газовой или паровой фазы в жидкую.

При перегонке и ректификации жидкая смесь разделяется на составляющие компоненты. Происходит переход веществ из жидкой фазы в паровую и из паровой в жидкую.

При экстракции происходит извлечение одного или нескольких веществ из растворов или твердых веществ с помощью растворителей. При экстракции в системе жидкость — жидкость имеет место переход вещества из одной жидкой фазы в другую жидкую фазу.

Процесс извлечения веществ из твердого тела с помощью растворителя называют выщелачиванием. При выщелачивании вещество переходит из твердой фазы в жидкую.

При адсорбции происходит избирательное поглощение газов, паров или растворенных в жидкостях веществ твердым поглотителем — адсорбентом, способным поглощать один или несколько компонентов из их смеси. Процесс используется во многих производствах, где из смеси газов, паров или растворенных веществ необходимо извлечь тот или иной компонент. При адсорбции вещества переходят из газовой или жидкой фазы в твердую.

Сушка — это удаление влаги из твердых или жидких влажных материалов путем ее испарения. В этом процессе имеет место переход влаги из твердого влажного материала в паровую или газовую фазу.

При кристаллизации из жидкой фазы выделяется вещество в виде кристаллов. При этом происходит переход вещества из жидкой фазы в твердую в результате возникновения и роста кристаллов в растворе.

12.2. КИНЕТИКА МАССОПЕРЕДАЧИ

Массопередача — процесс перехода вещества (или нескольких веществ) из одной фазы в другую в направлении достижения равновесия.

В массообмене участвуют, как минимум, три вещества: распределяющее вещество (или вещества), составляющее первую фазу; распределяющее вещество (или вещества), составляющее вторую фазу; распределяемое вещество (или вещества), которое переходит из одной фазы в другую.

Обозначим первую фазу , вторую — , а распределяемое вещество — М. Все массообменные процессы обратимы, поэтому распределяемое вещество может переходить из фазы в фазу и наоборот в зависимости от концентрации вещества в фазах.

Пусть распределяемое вещество находится первоначально только в фазе и имеет концентрацию . В фазе в начальный момент распределяемое вещество отсутствует, т. е. концентрация его в этой фазе .

Если распределяющие фазы привести в соприкосновение друг с другом, начинается переход распределяемого вещества из фазы в фазу и с появлением вещества М в фазе начинается обратный переход его из фазы в фазу . До некоторого момента времени число частиц распределяемого вещества М, переходящих в единицу времени из фазы в фазу , больше, чем число частиц, переходящих из фазы в фазу . Однако конечным результатом является переход вещества М из фазы в фазу . По истечении определенного времени скорости прямого и обратного перехода вещества М в фазах и становятся одинаковыми. Такое состояние системы называется равновесным. При равновесии устанавливается строго определенная зависимость между концентрациями распределяемого вещества в фазах. Такие концентрации называют равновесными.

При равновесии каждой концентрации соответствует равновесная концентрация , и наоборот, каждой концентрации соответствует определенная равновесная концентрация .

В условиях равновесия существуют определенные в каждом конкретном случае зависимости между концентрациями:

; . (12.1)

Эти зависимости определяются экспериментально и называются равновесными зависимостями.

Равновесные зависимости изображаются графически кривой или в частном случае прямой линией. На рис. 12.1 показана зависимость равновесной концентрации у компонента в газовой фазе от его концентрации в жидкой фазе при постоянных давлении и температуре.

Рис. 12.1 Диаграмма равновесия при p=const и t=const

Отношение концентраций компонента в фазах в условиях равновесия называется коэффициентом распределения.

Коэффициент распределения геометрически выражает тангенс угла наклона линии равновесия. В случае кривой линии равновесия коэффициент распределения является переменной величиной.

Конкретный вид законов равновесия применительно к различным процессам массопередачи будет рассматриваться в соответствующих главах.

Равновесные зависимости позволяют определить не только направление процесса, но и скорость перехода распределяемого вещества из одной фазы в другую.

Разность между фактической и равновесной концентрациями, характеризующая степень недостижения равновесия, является движущей силой массообменных процессов.

Расчет движущих сил и коэффициентов скорости массообменных процессов составляет кинетику массопередачи.

Основные уравнения массопередачи могут быть получены из общего уравнения кинетики. Согласно этому уравнению скорость массообменных процессов прямо пропорциональна движущей силе процесса и обратно пропорциональна диффузионному (массообменному) сопротивлению.

Обозначив величину, обратную диффузионному сопротивлению, через (где — диффузионное, или массообменное, сопротивление), запишем

, (12.2)

где: М – количество вещества, перешедшего из одной фазы в другую; F – площадь поверхности массопередачи; τ – продолжительность процесса; k – коэффициент скорости процесса, называемый в теории массопередачи; Δ – движущая сила.

Нетрудно видеть, что является скоростью массопередачи, отнесенной к единице контакта фаз.

Если отнесено к единице времени, имеем

. (12.3)

При для всей поверхности массообмена

. (12.4)

Уравнения (12.3) и (12.4) называют основными уравнениями массопередачи. Согласно этим уравнениям количество вещества, перенесенного из ядра одной фазы в ядро другой фазы, пропорционально разности его концентраций в ядрах фаз, площади поверхности фазового контакта и продолжительности процесса.

Коэффициент массопередачи показывает, какое количество вещества переходит из одной фазы в другую в единицу времени через единицу поверхности фазового контакта при движущей силе, равной единице.

Коэффициенты массопередачи в зависимости от единиц, в которых выражены движущая сила и количество распределяемого вещества, могут выражаться в м/с, кг/(ед. дв. силыс), кмоль/ (ед. дв. силыс).

12.3. МАТЕРИАЛЬНЫЙ БАЛАНС МАССООБМЕННЫХ ПРОЦЕССОВ

Рассмотрим схему элементарного массообменного аппарата, в котором происходит массообмен между двумя движущимися прямотоком фазами. Массовые скорости фаз относительно поверхности их раздела, выраженные в килограммах инертного вещества в час, обозначим и , а концентрации распределяемого вещества (в килограммах на килограмм инертного вещества) — соответственно и (рис. 12.2).

Рис. 12.2 К составлению материального баланса и выводу уравнения рабочей линии процесса:

а – схема потоков в аппарате; б – изображение рабочей линии в координатах y — x

Предположим, что , тогда распределяемое вещество будет переходить из фазы в фазу , а концентрация в фазе будет уменьшаться от до , соответственно концентрация в фазе увеличится от до .

Для бесконечно малой площади поверхности аппарата

. (12.5)

Интегрируя это уравнение в пределах изменения концентраций распределяемого вещества в аппарате, получим

, (12.6)

откуда определим массовые расходы

;

.

Интегрируя уравнение (12.5) в пределах от начальных до текущих концентраций, получим , откуда определим связь между текущими концентрациями

. (12.7)

Аналогично для противоточного движения фаз

,

где ; .

Из уравнений (12.7) и (12.8) легко видеть, что связь между текущими концентрациями распределяемого вещества подчиняется линейным уравнениям. Уравнение прямой, выражающее зависимость между фактическими (рабочими) концентрациями, называется рабочей линией процесса.

12.4. ОСНОВНЫЕ ЗАКОНЫ МАССОПЕРЕДАЧИ

В процессах массопередачи следует различать несколько случаев массообмена: между потоком газа или пара и потоком жидкости; между потоками жидкости; между потоками жидкости и твердой фазой; между потоками газа или пара и твердой фазой.

Основными законами массопередачи являются закон молекулярной диффузии (первый закон Фика), закон массоотдачи (закон Ньютона — Щукарева) и закон массопроводности.

Закон молекулярной диффузии (первый закон Фика), основанный на том, что диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, приводящего к переносу молекул распределяемого вещества из зоны высоких концентраций в зону низких концентраций, гласит: количество вещества, перенесенного путем диффузии, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и продолжительности процесса:

, (12.9)

где: dM – количество вещества, перенесённого путём диффузии; D – коэффициент пропорциональности, или коэффициент диффузии; — градиент концентрации в направлении диффузии; F – элементарная площадка, через которую происходит диффузия; dτ – продолжительность диффузии.

Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность в 1 в течение 1 ч при разности концентраций на расстоянии 1 м, равной единице.

Знак «минус» в правой части уравнения показывает, что при молекулярной диффузии концентрация убывает.

Если единицы измерений [М] = [кг], [Р] = [], [τ] = [ч], [С] = [кг/] и []=[м], то размерность коэффициента диффузии определится из уравнения (12.9):

.

Значения коэффициента диффузии обычно берут из справочников или находят по следующим формулам:

; (12.10)

, (12.11)

где: Т – температура, К; — давление, Па; и — мольные объемы взаимодействующих веществ, ; и — молекулярные массы веществ, кг/кмоль; — динамическая вязкость, , А и В — опытные константы, зависящие от природы вещества.

Коэффициенты диффузии зависят от агрегатного состояния систем. Для газов коэффициенты диффузии имеют значения (0,1. 1,0)10-4 . Они примерно на четыре порядка выше, чем для жидкостей. С увеличением температуры коэффициенты диффузии возрастают, а с повышением давления уменьшаются.

Коэффициенты диффузии в газах почти не зависят от концентрации, в то время как коэффициенты диффузии в жидкостях изменяются с изменением концентрации диффундирующего вещества.

Дифференциальное уравнение молекулярной диффузии (второй закон Фика) получают, рассмотрев материальный баланс по распределяемому веществу для элементарного параллелепипеда, выделенного мысленно в потоке одной из фаз (рис. 12.3).

Рис. 12.3. К выводу дифференциального уравнения молекулярной диффузии

Пусть через этот элементарный параллелепипед за счет молекулярной диффузии перемещается вещество. Если через грани , и проходят количества вещества, соответственно равные , , , то через противоположные грани выходят количества вещества , , , т. е. элементарный объем параллелепипеда приобретает диффундирующее вещество в количестве . При этом концентрация вещества повышается на . Согласно основному закону молекулярной диффузии (первый закон Фика)

;

.

.

Аналогично найдем разности между количествами вещества, прошедшего через другие противоположные грани параллелепипеда.

Общее количество приобретенного вещества

. (12.12)

Это же количество вещества можно найти умножением объема параллелепипеда на изменение концентрации диффундирующего вещества за время :

. (12.13)

Приравнивая уравнения (12.12) и (12.13), получим дифференциальное уравнение молекулярной диффузии

. (12.14)

Основной закон массоотдачи, который является аналогом закона Ньютона, был установлен русским ученым Щукаревым при изучении растворения твердых тел. Этот закон формулируется так: количество вещества, перенесенного потоком от поверхности раздела фаз (контакта фаз) в воспринимающую фазу или в обратном направлении, прямо пропорционально разности концентраций у поверхности контакта фаз и в ядре потока воспринимающей фазы, площади поверхности контакта фаз и продолжительности процесса.

Согласно теории диффузионного пограничного слоя распределяемое вещество переносится из ядра потока жидкости к поверхности раздела фаз непосредственно конвективными потоками жидкости и молекулярной диффузией. В рассматриваемой системе (рис. 12.4) различают ядро потока и приграничный диффузионный слой. В ядре перенос вещества осуществляется преимущественно потоками жидкости или газа. В условиях турбулентного течения потоков концентрация распределяемого вещества в данном сечении в условиях стационарного режима сохраняется постоянной. По мере приближения к пограничному диффузионному слою турбулентный перенос снижается и начинает увеличиваться перенос за счет молекулярной диффузии. При этом появляется градиент концентрации распределяемого вещества, растущий по мере приближения к границе. Таким образом, область пограничного диффузионного слоя — это область появления и роста градиента концентрации, область увеличения влияния скорости молекулярной диффузии на общую скорость массопередачи.

Рис.12.4. К выводу уравнения массоотдачи

Примем, что распределяемое вещество М переходит из фазы G, в которой его концентрация выше равновесной, в фазу L.

Если концентрации вещества в ядрах фаз принять равными и , а концентрации на поверхности раздела фаз — соответственно и , , то процесс массоотдачи вещества из ядра фазы G к поверхности раздела фаз и от поверхности раздела фаз в ядро фазы L можно записать так:

; (12.15)

,

где: , — коэффициенты массоотдачи, характеризующие перенос вещества конвективными и диффузионными потоками одновременно; концентрации и предполагаются равными равновесным, т. е. и .

Размерность коэффициента массоотдачи .

Коэффициент массоотдачи показывает, какое количество вещества передается от поверхности контакта фаз площадью в 1 в ядро воспринимающей фазы или в обратном направлении в течение единицы времени при разности движущих сил, равной единице.

По физическому смыслу коэффициенты массоотдачи отличаются от коэффициентов массопередачи, но выражаются в одинаковых единицах.

Для установившегося процесса выражает количество вещества, перенесенного от поверхности контакта фаз в ядро или из ядра потока к ее поверхности в единицу времени.

Для этого случая уравнение (12.15) перепишется так:

.

Если для всей поверхности контакта фаз,

. (12.16)

Если рассмотреть вновь элементарный объем фазы (см. рис. 12.3), перемещающийся в пограничном слое, то можно утверждать, что концентрация распределяемого вещества в нем меняется не только за счет молекулярной диффузии, но также и за счет турбулентного переноса его. В этом случае концентрация распределяемого вещества будет функцией не только координат и времени, как в случае только молекулярной диффузии, но и скорости перемещения.

Соответственно этому изменение концентрации G выразим через субстанциональную производную:

. (12.17)

В этом уравнении сумма членов характеризует конвективное изменение концентрации, а — локальное.

Увеличение количества распределяемого вещества за счет молекулярной диффузии определяется уравнением (12.14). Приравнивая уравнение (12.17) к (12.14) и заменяя локальное изменение концентрации на полное в (12.17), получим дифференциальное уравнение конвективной диффузии

. (12.18)

Для полного математического описания процесса это уравнение должно быть дополнено уравнением, характеризующим условие на границе раздела фаз.

Количество вещества, передаваемого из фазы в фазу у границы, определяется основным законом конвективной диффузии (12.15). У поверхности раздела фаз вещество переходит из фазы в фазу, как было установлено выше, за счет молекулярной диффузии [см. уравнение (12.9)]. Приравнивая эти уравнения, получим

, (12.19)

где: — движущая сила процесса.

Уравнение (12.19) характеризует условие массообмена на границе фазы и дополняет уравнение (12.18), являясь вместе с ним математическим описанием процесса конвективной диффузии.

Критериальные уравнения конвективной диффузии получают из уравнений (12.18) и (12.19).

Для получения диффузионных критериев, подобия воспользуемся методами теории подобия. Из уравнения (12.19) получим безразмерный комплекс , из которого после сокращения получают диффузионный критерий Нуссельта

, (12.20)

который характеризует условия на границе рассматриваемой фазы, т. е. выражает отношение интенсивности переноса вещества в ядре фазы конвективной диффузией к интенсивности переноса в диффузионном слое, где интенсивность переноса определяется молекулярной диффузией D.

Из дифференциального уравнения конвективной диффузии (12.18), разделив все члены на , получим безразмерные комплексы

и

и соответственно диффузионный критерий Фурье

(12.21)

и диффузионный критерий Пекле

. (12.22)

Критерий характеризует изменение скорости потока диффундирующей массы во времени и используется для характеристики нестационарных процессов диффузии. Преобразуем критерий и представим его в виде произведения

.

Диффузионный критерий Прандтля характеризует подобие полей физических величин и определяется только физическими свойствами вещества. Найдя критерии подобия, характеризующие явление массообмена, запишем общее критериальное уравнение конвективной диффузии

. (12.23)

Критерий Нуссельта в этом уравнении является определяемым в отличие от других критериев, которые являются определяющими, т. е. составленными целиком из параметров, входящих в условие однозначности. Коэффициент массоотдачи, входящий в критерий Нуссельта, не входит в условие однозначности и является искомой величиной.

В явном виде уравнение (12.23) перепишется так:

. (12.24)

Критерий Грасгофа в этом уравнении характеризует конвективную диффузию в условиях естественной конвекции.

В случае стационарных процессов из общего критериального уравнения исключается критерий Фурье и оно приобретает вид

. (12.25)

При вынужденном движении можно пренебречь естественной конвекцией. В этом случае из уравнения (12.25) выпадает критерий Грасгофа и уравнение приобретает вид

. (12.26)

Конкретные критериальные уравнения приводятся в соответствующих главах этой части.

По значениям критерия Нуссельта, найденным по критериальным уравнениям, определяют коэффициент массоотдачи

. (12.27)

Между переносом теплоты, массы и механической энергии существует, как отмечалось ранее, аналогия, эти процессы описываются однотипными дифференциальными уравнениями.

При рассмотрении движения потока жидкости в трубе различают пограничный слой и ядро потока. В ядре турбулентного потока происходит выравнивание скоростей по нормали к вектору скорости, в пограничном же слое происходит резкое изменение скорости потока до нуля. Такое же выравнивание температур и концентраций происходит в процессах тепло — и массопередачи. Таким образом, имеет место аналогия между этими процессами.

Исходя из этой аналогии, можно приближенно определять коэффициенты массоотдачи по данным о трении жидкостного потока или о скорости переноса теплоты.

На основании гидродинамической аналогии можно определить отношение коэффициента массоотдачи к средней скорости потока , которое представляет собой безразмерную величину и носит название диффузионного критерия Стантона

.

Критерий Стантона характеризует подобие полей концентраций и скоростей при массоотдаче в турбулентных потоках.

Существует связь между коэффициентом массопередачи и коэффициентами массоотдачи. Рассмотрим процесс массопередачи при переходе распределяемого вещества из фазы G в фазу L при условии линейных зависимостей между рабочими и равновесными концентрациями (см. рис. 12.4). Примем, что на границе раздела фаз достигается равновесие.

Количество вещества, перемещающегося из фазы G к поверхности на границе раздела фаз, может быть определено по уравнению

,

где: — коэффициент массоотдачи для фазы, G.

Количество распределяемого вещества, перемещающегося от элемента поверхности в фазу L, может быть вычислено также по фазе L по уравнению (12.15). В этом случае движущую силу следует выразить разностью :

,

где: — коэффициент массоотдачи для фазы L.

Так как известна равновесная зависимость , концентрацию в фазе L можно выразить через равновесную в фазе G:

.

.

Сложим левые и правые части этих уравнений

,

так как .

Из основного уравнения массопередачи (12.4) получим

.

Приравнивая правые части уравнения, получим

или . (12.28)

Рассуждая аналогично, для фазы L будем иметь

или . (12.29)

Левые части этих уравнений представляют собой общее диффузионное сопротивление переносу, а их правые части — сумму диффузионных сопротивлений массоотдаче в фазах. Зависимости (12.28) и (12.29) являются поэтому уравнениями аддитивности фазовых сопротивлений.

Коэффициенты и связаны соотношением . Числовые значения коэффициентов массопередачи определяются значениями коэффициентов массоотдачи и углом наклона равновесной линии. Коэффициенты массоотдачи определяют по критериальным уравнениям.

12.5. МАССОПЕРЕДАЧА С ТВЕРДОЙ ФАЗОЙ

К этим процессам относятся экстракция из твердых пористых материалов (выщелачивание), сушка и адсорбция.

Массоперенос в твердом пористом материале представляет собой неустановившийся процесс.

Перенос вещества из твердого капиллярно-пористого тела через границу раздела фаз в газовую (паровую) среду (сушка), в жидкую (экстракция) или из газовой (паровой) среды в твердое тело (адсорбция) происходит при наличии градиента потенциала переноса в направлении достижения равновесия.

На перенос вещества значительное влияние оказывает его структура. Твердое пористое тело представляет собой систему со сложными многообразными геометрическими характеристиками, главными из которых являются пористость, полидисперсность, распределение пор по размерам, форма капилляров.

В зависимости от капиллярно-пористой структуры твердые материалы классифицированы в порядке уменьшения величины критического диаметра пор, которому соответствуют усложнение внутренней структуры твердого тела и увеличение внутридиффузионного сопротивления, на широкопористые ( до 100 нм), среднепористые и материалы с ультрамикропорами.

В общем случае перенос вещества внутри пористого твердого тела осуществляется как в паровой, так и в жидкой фазе. В случае десорбции влаги при небольшой влажности материала влага перемещается в основном за счет молекулярного переноса пара. При большой влажности материала перемещение жидкости и пара обусловлено явлениями с различными механизмами переноса: капиллярными, осмотическими, термокапиллярными, гравитационными потоками газовой (паровой) фазы.

Значение каждого из перечисленных механизмов переноса зависит от капиллярно-пористой структуры твердого тела и режима проведения процесса.

Массоперенос в системе с твердой фазой рассмотрим на примере десорбции влаги из твердого тела на следующей схеме (рис. 12.5).

Рис.12.5. Модель массопереноса вещества в капиллярно-пористом теле

В начальный момент времени концентрация распределяемого вещества постоянная во всем объеме пластины и равна . Концентрация распределяемого вещества в омывающей твердое тело фазе постоянна и равняется . При начальной концентрации вещества в твердом теле , большей равновесной концентрации, соответствующей концентрации в омывающей фазе, распределяемое вещество перемещается в омывающую фазу с поверхности раздела фаз.

При удалении свободной поверхностной влаги температура материала не меняется и равна температуре мокрого термометра, а давление паров над материалом равно давлению насыщенных паров жидкости. В этот период влага удаляется из твердого материала при постоянной скорости.

С течением времени концентрация вещества в твердом теле непрерывно снижается, принимая значения , . Начиная с некоторой критической концентрации , наблюдается продвижение зоны испарения в глубь тела, что приводит к уменьшению градиента потенциала переноса и к замедлению процесса.

Удаление влаги происходит не только в продвигающейся внутрь тела поверхности испарения с переменной координатой , но и во всей толщине «отработанного слоя», постепенно уменьшаясь по мере приближения к поверхности тела. Это явление объясняется различными формами связи влаги с материалом.

В период уменьшения скорости общая скорость массопереноса будет определяться скоростью перемещения общего массового потока вещества от поверхности испарения к поверхности тела, т. е. скоростью массопроводности, которая определяется механизмом массопереноса.

Процесс массопроводности описывается уравнением, аналогичным закону Фика (Фурье),

, (12.30)

в котором называется коэффициентом массопроводности. Здесь Х — концентрация распределяемого вещества в твердом теле; t — температура тела.

В процессах адсорбции коэффициент массопроводности значительно зависит от степени насыщения адсорбента адсорбтивом и температуры.

В процессах экстрагирования тепловые эффекты незначительны, что позволяет рассматривать процесс массопереноса как изотермический. Это обстоятельство облегчает анализ и расчет кинетики процесса.

Наиболее сложным процессом массопереноса с твердой фазой является сушка, представляющая собой взаимосвязанный тепломассообменный процесс.

Дифференциальное уравнение массопроводности, которое выводится аналогично дифференциальному уравнению теплопроводности, имеет вид

. (12.31)

Условия на границе сформулируем так: к элементарной площадке на границе раздела фаз подводится из твердой фазы вещество в количестве , которое определяется уравнением (12.30). Это вещество отводится в омывающую фазу за cчет конвективной диффузии, т. е. . Приравнивая к этому выражению уравнение (3.1.30) и проводя преобразования, получим

/

Методом теории подобия получим безразмерный комплекс

, (12.32)

который называется диффузионным критерием Био.

Из уравнения массопроводности получим диффузионный критерий Фурье

Критерий Био показывает соотношение между скоростью перемещения вещества от поверхности фаз в омывающую фазу, которая характеризуется коэффициентом массоотдачи , и скоростью массопроводности.

Критерий Фурье характеризует изменение скорости массопереноса внутри твердого тела во времени.

При подобии процессов массопроводности должно соблюдаться геометрическое подобие, которое для одномерного потока выражается как , где — координата; R — определяющий размер твердого тела. Определяемой величиной является безразмерная концентрация: , где Х — концентрация в данной точке твердой фазы в момент времени .

Для одномерного потока критериальное уравнение массопроводности запишется так:

. (12.34)

Аналитическое решение уравнения (12.34) имеется только для твердых тел простейшей формы: неограниченной пластины, бесконечного цилиндра и шара. Для облегчения расчетов составлены для этих тел графики, позволяющие определить по критериям и безразмерные концентрации.

В зависимости от структуры капиллярно-пористого тела, режима процесса, концентрации вещества в твердой фазе стадией, определяющей скорость процесса, может быть внешний либо внутренний массоперенос либо скорость общего процесса будет определяться обеими стадиями процесса одновременно. Для характеристики влияния внутреннего и внешнего массопереноса на кинетику процесса служит значение критерия Био, которое представляет отношение внешнедиффузионного сопротивления массопереносу к внутридиффузионному.

Для описания массопередачи в системе с твердой фазой в первом приближении может быть использовано основное уравнение массопередачи (12.4).

Коэффициент массопередачи рассчитывают, например, по уравнению

, (12.35)

в котором — коэффициент формы, равный для пластины 1, для цилиндра 2, для шара 3; — показатель степени в уравнении распределения концентраций в твердом теле.

При проведении процесса во внешнедиффузионной области, когда , уравнение (12.35) преобразуется так:

. (12.36)

В этом случае скорость процесса целиком определяется внешнедиффузионными факторами.

При одновременном течении процессов тепло — и массообмена для определения коэффициентов тепломассоотдачи предложены критериальные уравнения вида

, (12.37)

где: — критерий Гухмана, характеризующий объемное испарение жидкости в адиабатических условиях. Значения А и зависят от гидродинамического режима в аппарате.

При лимитирующей стадией является массопроводность внутри материала и из (12.35) следует

, (12.38)

где: .

Сложность связи коэффициента массопроводности с влажностью материала и температурой процесса обусловливает экспериментальное определение коэффициента массопроводности для каждого материала. Для ряда капиллярно-пористых материалов накоплено большое количество экспериментальных данных по коэффициентам массопроводности.

12.6. ДВИЖУЩАЯ СИЛА МАССООБМЕННЫХ ПРОЦЕССОВ

Движущая сила массообменных процессов, как было сказано, определяется степенью отклонения от равновесия, которое вычисляется как разность между рабочей и равновесной концентрациями или, наоборот, равновесной и рабочей в зависимости от того, какие значения из них больше. Движущую силу можно выразить через концентрации распределяемого вещества в фазе G через у или в фазе L через Х.

Различают локальные движущие силы, вычисленные для массообменного процесса, протекающего на бесконечно малой площади контакта фаз, и движущие силы для всего процесса массообмена в пределах изменения концентраций от начальных до конечных.

Локальные движущие силы изменяются с изменением концентраций, поэтому для всего процесса массообмена вычисляют средние движущие силы.

Выражение и значение средней движущей силы зависят от вида уравнения равновесия.

Рассмотрим определение средней движущей силы, когда линия равновесия определяется уравнением кривой (рис. 12.6) в противоточном массообменном аппарате при условии .

Рис. 12.6. Изображение рабочей и равновесной линий в координатах y-x

Примем, что расходы фаз G и L постоянны, коэффициенты массопередачи и не меняются по длине аппарата, и перенос вещества происходит из фазы G в фазу L.

Для элемента поверхности на основании уравнения материального баланса (12.5) можно записать .

Разделяя переменные и F и интегрируя это выражение в пределах изменения концентрации от до (см. рис. 12.1) и поверхности контакта фаз от 0 до F, получим

, (12.39)

. (12.40)

Согласно уравнению материального баланса (12.6) количество вещества, перешедшего из фазы G в фазу L, равно . Подставим G из последнего выражения в уравнение (12.40)

,

; (12.41)

. (12.42)

Аналогично можно определить среднюю движущую силу в концентрациях в фазе L

. (12.43)

Интеграл в знаменателе уравнений (12.42) и (12.43) называется числом единиц переноса :

; (12.44)

. (12.45)

Из уравнений (12.41), (12.42), (12.44) и (12.45) находят соотношения между средней движущей силой и числом единиц переноса:

. (12.46)

Сопоставляя уравнение (12.41) с основным уравнением массопередачи (12.2), найдем выражения средних движущих сил массопередачи

. (12.47)

Из уравнений (12.46) и (12.47) следует, что число единиц переноса обратно пропорционально средней движущей силе процесса.

Из уравнений (12.46) и (12.47) также следует, что число единиц переноса характеризует изменение рабочих концентраций на единицу движущей силы.

В уравнениях (12.42) и (12.43) знаменатель дробей находят графическим интегрированием. Так, например, в пределах концентраций , через определенные интервалы для ряда значений у находят соответствующие им величины х, , и .

На диаграмме в координатах строят кривую, как показано на рис. 12.7. Площадь под кривой, ограниченная ординатами и умноженная на масштаб диаграммы и , дает искомый интеграл

. (12.48)

Рис. 12.7. К определению числа единиц переноса графическим интегрированием

Ниже будет показано, что число единиц переноса используют для расчета высоты массообменных аппаратов, особенно когда поверхность контакта фаз трудно определить.

В частных случаях, например при массопередаче в разбавленных растворах (адсорбция, экстракция), а также при расчете массообменных аппаратов, когда для упрощения расчетов аппроксимируют линию равновесия прямой, средняя движущая сила массопередачи определяется, как и при расчете теплообменных аппаратов, как средняя логарифмическая или средняя арифметическая величина из движущих сил на входе и выходе из аппарата.

Рассмотрим расчет средних движущих сил при различных схемах взаимодействия потоков.

На рис. 12.8,а приведена общая схема изменения концентраций при противоточном взаимодействии потоков.

Рис. 12.8. Схемы массообмена и условия отсчета движущих сил:

а – при противотоке; б – при прямотоке

В этом случае средние движущие силы в — м элементе аппарата определяются так:

; (12.49)

. (12.50)

В случае прямотока (рис. 12.8, б)

; (12.51)

. (12.52)

При расчете движущей силы при перекрестном токе взаимодействующих фаз принимают в большинстве случаев одну из схем изменения концентраций фаз в аппарате, а именно: обе фазы на элементе аппарата идеально перемешаны; газ (пар) идеально перемешан, а в фазе, протекающей через элемент аппарата, концентрация меняется линейно; фаза, перетекающая через элемент аппарата, идеально перемешана, а в газе (паре), пронизывающем перетекающий поток, концентрация меняется линейно.

Схема массообмена на элементе аппарата и условия отсчета движущих ил приведены на рис. 12.9.

На — й элемент поступает фаза концентрацией . В результате массообмена с поступающим с нижележащего элемента газом (паром) с концентрацией концентрация в жидкой фазе изменяется до конечной, равной , а концентрация в паре изменяется до .

В случае, когда обе фазы на элементе аппарата идеально перемешаны, средняя движущая сила определяется так:

; (12.53)

.

Условия отсчета движущей силы для случая, когда жидкая фаза идеально перемешана на элементе и имеет концентрацию, равную концентрации на выходе, а газ (пар) линейно меняет концентрацию от до , представлены на рис. 12.9.

Рис. 12.9. Схема массообмена и условия отсчета движущих сил при перекрестном токе:

а – жидкая фаза идеально перемешана, а пар (газ) идеально вытесняется в слое; б – обе фазы идеально перемешаны

Следует отметить, что эта схема изменения концентраций в фазах соответствует процессу в аппаратах перекрестного тока небольших диаметров.

На таком представлении о характере взаимодействия фаз основан ряд методов расчета размеров аппаратов. В этом случае движущие силы определяются так:

; . (12.54)

Для случая идеального вытеснения потоков средние движущие силы в аппарате (рис. 12.9,б) будут определяться как средние логарифмические из движущих сил на входе потока и на выходе из аппарата. Граничные локальные движущие силы в аппарате при линейном изменении концентраций в паре (газе) определяются уравнениями. Среднюю движущую силу с учетом выражений (12.54) можно получить в виде

; (12.55)

Расчет движущей силы из принятых условных схем взаимодействия потоков приводит, как правило, к погрешностям в определении площади рабочей поверхности аппарата.

Все реальные аппараты, как было отмечено выше, в большинстве случаев относятся по гидродинамической характеристике к аппаратам промежуточного типа, в которых движущая сила зависит от распределения концентраций и температур в рабочей зоне аппарата.

Общим для рассмотренных выше схем изменения концентраций в фазах является то, что ни одна из них не учитывает реальной гидродинамической обстановки в аппарате.

Действительную движущую силу можно определить на основании гидродинамических моделей и экспериментальных данных по перемешиванию фаз на контактном устройстве.

Коэффициент использования движущей силы в прямо — и противоточных аппаратах

, (12.56)

где:, — движущие силы на входе и выходе из -го контактного устройства.

Для аппаратов перекрестного тока соответственно получено выражение

. (12.57)

Из уравнения (12.57) по фазе L, например, при получим

. (12.58)

Из последнего уравнения можно получить выражение, удобное для расчетов,

. (12.59)

где: и А — тангенсы углов наклона равновесной и рабочей линий; — число единиц переноса по фазе G, вычисленное при условии идеального перемешивания газовой (паровой) фазы; N — количество псевдосекций.

В некоторых массообменных аппаратах, например в насадочных, тарельчатых, площадь поверхности фазового контакта трудно определить. В этих случаях для их расчета используют модифицированные уравнения массопередачи.

Площадь поверхности фазового контакта в таких аппаратах

,

где: — объем аппарата, ; — удельная поверхность фазового контакта, .

Подставляя величину F в уравнение массопередачи (12.4), получим

. (12.60)

Величины и называют объемными коэффициентами массопередачи, соответственно и — объемными коэффициентами массоотдачи.

Из уравнения (12.60) получают

, или ,

где: и — объемные коэффициенты массопередачи.

Представив , можно из (12.41) определить высоту массообменного аппарата, имея в виду, что :

, (12.61)

где: — площадь поперечного сечения аппарата, .

Величина представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП), и измеряется в единицах высоты. В случае выражения числа единиц переноса в концентрациях х эта величина равна . С учетом этого модифицированные уравнения массопередачи принимают вид

;

. (12.62)

Сопоставление полученных уравнений (12.62) с основным уравнением массопередачи показывает, что высота, эквивалентная единице переноса или , обратно пропорциональна объемному коэффициенту массопередачи.

Таким образом, чем выше коэффициент массопередачи, тем ниже величина ВЕП.

12.7. РАСЧЕТ ОСНОВНЫХ РАЗМЕРОВ МАССООБМЕННЫХ АППАРАТОВ

Для расчета высоты противоточных колонных аппаратов (тарельчатые и насадочные абсорбционные и ректификационные, экстракционные аппараты) требуется определить число ступеней изменения концентраций (тарелок) по высоте аппарата.

Число теоретических ступеней может быть определено аналитическим или графическим методом. Часто пользуются таким понятием, как теоретическая ступень изменения концентраций, или теоретическая тарелка. При этом предполагается, что на этой гипотетической ступени контакта фаз жидкость идеально перемешана, а концентрации взаимодействующих фаз достигают равновесных значений.

Рассмотрим процесс массообмена на -й тарелке (рис. 12.10,а). На тарелку поступают газовая фаза G концентрацией и жидкая фаза L концентрацией . В результате массообмена концентрация в газовой фазе снижается до величины , а в жидкой увеличивается до .

В случае достижения равновесия между составом удаляющегося с тарелки газа , и составом стекающей с нее жидкости , их концентрации изображаются на рис. 12.10, б точкой В, лежащей на линии равновесия.

Изменению концентраций в газовой фазе на теоретической ступени соответствует вертикальный отрезок . Изменение же концентрации в жидкой фазе от до изобразится горизонтальным отрезом .

Рис.12.10. Схема массообмена на тарелке (а) и изображение процесса в координатах y-x (б) – в условиях достижения равновесия на тарелке – идеальный процесс; в – в условиях недостижения равновесия на тарелке – реальный процесс

Таким образом, «ступенька» изображает изменение концентрации в обеих фазах на теоретической тарелке. Для определения числа теоретических тарелок в колонном аппарате строят последовательно такие «ступеньки», начиная от точки, характеризующей начальные концентрации в газовой и жидкой фазах, до точки, отвечающей конечным концентрациям в газовой и жидкой фазах.

Для определения числа действительных тарелок используют коэффициент полезного действия аппарата, который учитывает реальную кинетику массообмена на действительной тарелке. Значения КПД для различных конструкций тарелок находятся опытным путем и колеблются от 0,3.до 0,8.

Число действительных тарелок с учетом КПД определяется соотношением

, (12.63)

где: — число теоретических тарелок; — КПД.

Коэффициент полезного действия тарелки зависит от конструкции тарелки, физико-химических свойств жидкости и газа, взаимодействующих на тарелке, а также от гидродинамики потоков.

Следует иметь в виду, что расчет высоты аппарата с помощью теоретических тарелок (ступеней) является приближенным и его возможно применять, когда отсутствуют данные о коэффициентах массопередачи или имеются надежные данные о КПД для данных систем промышленных аппаратов.

В действительности равновесие при проведении массообменных процессов не достигается. Поэтому задача заключается в определении действительных ступеней контакта.

Эффективность ступени изменения концентраций выражается отношением изменения концентрации распределяемого вещества в одной фазе на ступени к движущей силе на входе фазы в ступень. Изменение концентраций на -й тарелке выразится как разность (отрезок на рис. 12.10,в), а движущая сила при идеальном перемешивании жидкости на тарелке — (отрезок на рис. 12.10,в).

Тогда эффективность ступеней (КПД по Мерфри)

.

Эффективность ступени представляет собой отношение действительного изменения концентраций на ступенях контакта фаз к максимально возможному.

. (12.64)

Рассмотрим определение числа действительных ступеней изменения концентраций с помощью построения кинетической линии.

Движущая сила для -й тарелки определится в соответствии с уравнением (12.54) при :

. (12.65)

Соответственно число единиц переноса

, (12.66)

. (12.67)

Из рис. 12.10 видно, что , или . Зная величину , можно найти по отрезку ВС положение точки В, а также В1, В2 и т. д. Соединив точки В, В1, В2, . линией, получим кинетическую линию процесса, которая характеризует концентрации фазы на выходе с каждой тарелки.

Для определения числа действительных ступеней изменения концентраций впишем в пределах заданных концентраций (точки М и N на рис. 12.11) ступенчатую линию. Число ступеней и определит число действительных ступеней изменения концентраций.

Рис. 12.11. К определению числа ступеней изменения концентраций методом построения кинетической линии

Рабочая высота аппарата

, (12.68)

где: — расстояние между тарелками, м.

Для построения кинетической линии необходимо знать число единиц переноса, или эффективность ступени. Число единиц переноса определяется из основного уравнения массопередачи, записанного для одной тарелки в виде .

Площадь поверхности контакта фаз в случае барботажа определить труднее. Поэтому коэффициент массопередачи относят к площади барботажа тарелки и обозначают , а число единиц переноса — как .

Коэффициент массопередачи рассчитывают с учетом известных коэффициентов массоотдачи и по уравнению аддитивности (12.28)

Таким образом, положение кинетической линии можно найти, определив и вычислив значение и величины отрезков СВ.

, (12.69)

где: G — расход газа, кг/ч; — плотность газа, ; v — линейная скорость газа (пара) в свободном сечении колонны, м/с.

Между эффективностью ступеней и числом единиц переноса существует следующая связь:

,

. (12.70)

1. Какие признаки объединяют все массообменные процессы? 2. В каком направлении протекают массообменные процессы? Как выражается движущая сила процесса? 3. Каков физический смысл коэффициентов массопередачи и массоотдачи? Какая существует между ними связь? 4. Что характеризует рабочая и равновесная линии процесса? 5. Как изобразить процесс массопередачи графически? 6. Какими законами описывается перенос вещества из ядра потока и поверхности раздела фаз? 7. Какой закон описывает молекулярную диффузию? 8. Как можно определить, когда процесс протекает во внутридиффузионной области, а когда — во внешнедиффузионной? 9. Почему в расчетной практике пользуются не дифференциальными уравнениями массопереноса, а критериальными? 10. Почему при расчете массообменных аппаратов оперируют со средней движущей силой процесса? 11. В каких случаях среднюю движущую силу определяют через число единиц переноса? 12. В каких случаях возможно определять среднюю движущую силу как среднелогарифмическую? 13. Какие принимаются схемы изменения концентрации распределяемого вещества во взаимодействующих фазах в массообменных аппаратах при выводе уравнений средних движущих сил? 14. Оцените, какая движущая сила будет больше в случае, когда обе фазы идеально перемешаны или когда, например, пар идеально вытесняется в слое идеально перемешанной жидкости. 15. Почему изложенные в лекции схемы изменения концентраций распределяемого вещества в фазах только приблизительно учитывают реальную гидродинамическую обстановку в аппарате?

Видео:Основы массорепедачи. Первая лекцияСкачать

Уравнения массоотдачи и массопередачи

В связи со сложностью механизма массоотдачи в практических расчетах используют относительно простое уравнение массоотдачи:

Т.е. скорость массоотдачи (кг/с) пропорциональна межфазной поверхности и средней разности концентраций на этой поверхности и в ядре фазы.

— средние концентрации в ядре фаз;

— концентрации на межфазной повер

— коэффициенты массоотдачи в фазах .

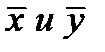
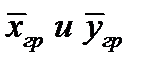
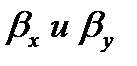
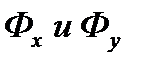
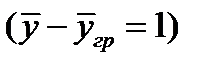
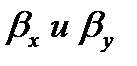
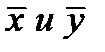
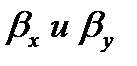
Коэффициент массоотдачи равен количеству вещества, отдаваемого межфазной поверхности в фазу за 1сек. при единичной движущей силе . Размерность зависит от размерностей М, . Например, [β] = [кг/м 2 ∙с∙(единица движущей силы)]. — функции многих переменных (ρ, ν, Re, Г₁, Г₂, Г₃…).

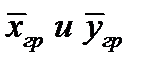
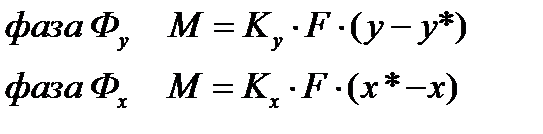
Т.к практически измерить невозможно, в основное уравнение массопередачи вместо этих концентраций вводят равновесные концентрации x * и y * :

,

где y * и x * — равновесные концентрации в данной фазе, соответствующие концентрациям в ядре другой фазы; K_y и K_x – коэффициенты массопередачи, соответствующие концентрациям распределяемого вещества в фазах .

Т.е. движущая сила процесса массопереноса, выражающая отклонение системы от равновесия, равна разности рабочей и равновесной концентраций вещества в данной фазе. Размерности коэффициентов массоотдачи и массопередачи одинаковы.

Движущая сила массопереноса – величина переменная, т.к. концентрации изменяются вдоль межфазной поверхности. Поэтому пользуются средней движущей силой:

— основное уравнение массопередачи.

Из основного уравнения массопередачи обычно определяют F.

Пусть линия равновесия описывается уравнением y * = m∙x, где m – тангенс угла наклона равновесной линии. Тогда коэффициенты массопередачи и массоотдачи связаны уравнениями аддитивности фазовых сопротивлений:

— для фазы Ф_у.

— для фазы Ф_х, где — сопротивление массопередаче; — сопротивление массоотдачи в фазах. .

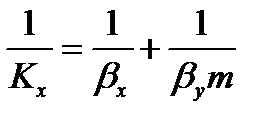
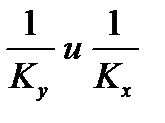
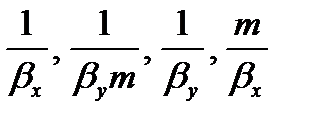
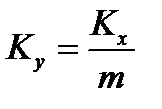
Для кривой линии равновесия m, K_x, K_y изменяются по высоте аппарата. В этом случае используют К_ср.

Иногда сопротивление одной из фаз очень мало, и тогда .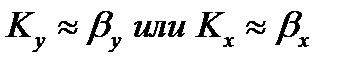

Повысить скорость массопередачи можно увеличением скорости потока той фазы, сопротивление которой больше.

Аддитивность фазовых сопротивлений нарушается при значительном сопротивлении межфазной поверхности.

Основное уравнение массопередачи аналогично основному уравнению теплопередачи: .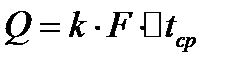

Видео:Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Лекция 4. Основы массопередачи

4.1. Общие сведения о массообменных процессах

Технологические процессы, скорость протекания которых определяется скоростью переноса вещества из одной фазы в другую, называются массообменными, а аппараты, в которых происходят эти процессы – массообменными аппаратами.

В массообменном аппарате могут производиться разнообразные процессы. Основными и важнейшими из них являются абсорбция, ректификация, экстракция, кристаллизация, адсорбция, сушка, ионнообменные процессы и мембранное разделение.

Абсорбцией называется процесс разделения, основанный на избирательном поглощении газов или паров жидкими поглотителями – адсорбентами. Этот процесс применяется во многих производствах, в которых из смеси газов необходимо извлечь какое-либо вещество или комплекс веществ. В процессе абсорбции имеет место переход вещества или группы веществ из газовой (паровой) фазы в жидкую. Обратный процесс называется десорбцией.

Ректификацией называется процесс разделения смеси жидкостей, имеющих различные температуры кипения при соответствующем давлении, на чистые или обогащенные составляющие в результате противоточного движения потоков пара и жидкости. Процесс имеет большое значение в тех производствах, в которых необходимо частичное или полное разделение жидких однородных смесей на чистые компоненты или их группы. В процессе ректификации имеет место переход вещества или группы веществ из жидкой фазы в паровую, и наоборот.

Экстракцией называется процесс разделения, основанный на извлечении растворенного в одной жидкости вещества или группы веществ, другой жидкостью, которая не смешивается или только частично смешивается с первой. Процесс применяется в тех случаях, когда из раствора необходимо извлечь растворенное вещество или группу веществ. В этом процессе имеет место переход вещества из одной жидкой фазы в другую жидкую фазу.

Адсорбцией называется процесс разделения, основанный на избирательном поглощении газов, паров или растворенных в жидкостях веществ, твердым пористым поглотителем – адсорбентом, способным поглощать одно или несколько веществ из их смеси. Процесс используется в тех производствах, где из смеси газов, паров или растворенных веществ необходимо извлечение того или иного вещества. В этом процессе вещества переходят из газовой или жидкой фаз в твердую. Ионнообменный процесс представляет собой процесс извлечения вещества из раствора, основанный на способности некоторых твердых веществ (ионитов) обменивать свои подвижные ионы на ионы извлекаемого вещества. Процесс применяется для извлечения веществ, находящихся в растворах, в малых концентрациях. В этом процессе вещества переходят из жидкой фазы в твердую.

Сушкой называется процесс удаления влаги из твердых влажных материалов путем ее испарения. Процесс необходим для тех производств, в которых влажные природные вещества предварительно до их переработки или готовые вещества в последней стадии производства должны быть обезвожены. В этом процессе имеет место переход влаги из твердого влажного материала в паровую или газовую фазу.

Кристаллизацией называется процесс разделения, основанный на выделении вещества из жидкой фазы в виде твердой фазы (кристаллов). Процесс имеет место в тех случаях, где требуется получение веществ повышенной чистоты. В этом процессе происходит переход вещества из жидкой фазы в твердую фазу. Обратный процесс – растворение.

Мембранное разделение основано на способности определенных тонких пленок (полупроницаемых мембран) пропускать одни вещества и задерживать другие. В этом процессе вещества переходят через полупроницаемую мембрану из исходной жидкости или газа в выделяемую жидкую или газовую фазу.

Из краткой характеристики следует, что для всех массообменных процессов характерным является переход вещества из одной фазы в другую, или массопередача.

Процессы массопередачи делятся на две группы. К одной группе процессов относятся (например, перегонка, кристаллизация), в которых минимально два вещества, составляющие две фазы, обмениваются компонентами, и непосредственно сами участвуют в массопередаче. В другой группе процессов в большинстве случаев в массопередаче участвуют три вещества: распределяющее вещество (или вещества), составляющие первую фазу; распределяющее вещество (или вещества), составляющие вторую фазу; распределяемое вещество (или вещества), которое переходит из одной фазы в другую. К этой группе относятся процессы: абсорбции, экстракции, адсорбции, сушки.

Одну фазу обозначим буквой G, другую L, а распределяемый компонент М. Поскольку все массообменные процессы обратимы, то распределяемое вещество может переходить в зависимости от концентрации этого вещества в распределяющих фазах из фазы G в фазу L и, наоборот.

Представим для первой группы процессов массопередачи, что распределяемое вещество находится вначале только в фазе G и имеет концентрацию . В фазе L в начальный момент распределяемого вещества нет и, следовательно, концентрация его в этой фазе =0.

Если распределяющие фазы привести в соприкосновение, начнется переход распределяемого вещества из фазы G в фазу L, и, в жидкой фазе появится распределяемый компонент с концентрацией отличной от нуля. С момента появления вещества М в фазе L начинается обратный переход его в фазу G. До некоторого момента времени число частиц М, переходящих в единицу времени через единицу поверхности фазового контакта из фазы G в фазу L, больше, чем число частиц, переходящих обратно из фазы L в фазу G.

Через определенный промежуток времени скорости перехода распределяемого вещества из фазы G в фазу L и обратно становятся одинаковыми. Такое состояние называется равновесным. В состоянии равновесия существует строго определенная зависимость между концентрациями распределяемого вещества в фазах, которые при равновесии системы называются равновесными.

Любой концентрации соответствует равновесная концентрация ( ), и наоборот, любой концентрации соответствует равновесная концентрация ( ), т.е. имеют место зависимости вида:

или .

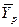
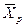
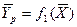
Условия равновесия и равновесные зависимости могут быть выражены не только через концентрации, но и через другие параметры, например, энтальпии, химический потенциал.

Знание равновесных концентраций позволяет установить направление течения процесса, которое определяется стремлением к равновесию. Если > и, следовательно, , распределяемое вещество М будет переходить из фазы G в фазу L. При условии 3 фазы — мольная объемная концентрация; в кг распределяемого компонента/м 3 фазы — массовая объемная концентрация.

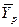
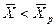
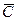
Вполне очевидно, что в зависимости от способа выражения концентраций численное значение движущей силы меняется. Между концентрациями существует связь, которая может быть получена в виде простых математических соотношений из физического смысла концентраций.

Например, если рассматривать смесь состоящую из двух компонентов А и В, то связь массовых долей с мольными, и наоборот, определяется по следующим зависимостям:

; .

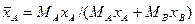
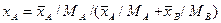
Соответственно связь относительных массовых и массовых долей

,

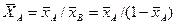
объемных концентраций и массовых долей

.

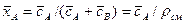
4.1.1. Основное уравнение массопередачи

Основной закон массопередачи, исходя из общих кинетических закономерностей, формулируется следующим образом: скорость (интенсивность) процесса прямо пропорциональна движущей силе и обратно пропорциональна сопротивлению процесса

, (4.1)

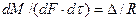
где — количество вещества, перешедшего из одной фазы в другую;

— элементарная поверхность фазового контакта; — промежуток времени; — движущая сила процесса ( или , или разность, выраженная через другие концентрации ); — сопротивление процессу.

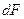
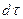
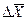
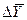
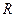
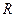
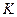
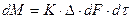
Если вместо принять обратную величину – коэффициент скорости процесса (коэффициент массопередачи) и записать уравнение относительно количества вещества, перешедшего из одной фазы в другую

. (4.2)

Уравнения (4.1) и (4.2) называют основными уравнениями массопередачи.

В аппаратуре, используемой для проведения массообменных процессов, равновесные концентрации не достигаются. Рабочие концентрации распределяемого компонента всегда отличаются от равновесных.

Разность между рабочими равновесными и рабочими концентрациями или, наоборот, характеризующими степень отклонения от равновесия, представляют собой движущую силу массообменных процессов.

4.1.2. Материальный баланс массообменных процессов

Материальный баланс массообменных процессов может быть составлен на основании следующих рассуждений. Рассмотрим взаимодействие двух движущихся фаз с массовыми расходами G — газообразной и L – жидкой, с концентрациями распределяемого компонента и кг/кг инертных компонентов распределяющих фаз.

При > и отсутствии потерь в процессе взаимодействия фаз при параллельных потоках вдоль поверхности раздела концентрация распределяемого компонента в газовой фазе уменьшается, а в жидкой — увеличивается (рис.4.1).

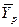
Для элемента поверхности

. (4.3)

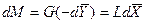
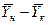
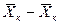
Интегрируя уравнение (4.3) в пределах от начальных до конечных концентраций и , получим

(4.4)

Интегрируя уравнение (4.3) в пределах от начальных до текущих значений концентраций и , получим

.

(4.5)

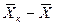
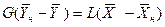
Рис.4.1. Изменение концентраций распределяемого компонента

при прямоточном движении фаз.

Аналогично для противоточного взаимодействия фаз можно получить уравнение

, (4.6)

,

, .

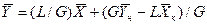
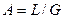
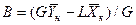
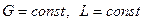
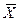
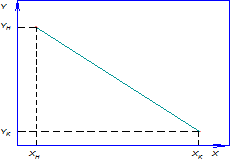
Так как расходы инертных компонентов носителей газообразной и жидкой фаз постоянны ( ), из уравнений (4.5) и (4.6) следует, что рабочие концентрации распределяемого вещества в фазах G и L связаны линейной зависимостью. Поэтому процессы массообмена удобно представлять графически в координатах (рис. 4.2). Уравнение прямой, выражающее зависимость между рабочими концентрациями, называется рабочей линией процесса.

Рис. 4.2. Уравнение рабочей линии процесса.

4.1.3. Движущая сила массообменных процессов

Движущей силой массообменных процессов является разность между рабочей и равновесной концентрациями или, наоборот. Это зависит от того, которая из указанных концентраций больше.

На рис.4.3 приведены возможные варианты выражения движущей силы массообменного процесса при одном и том же направлении перехода распределяемого вещества.

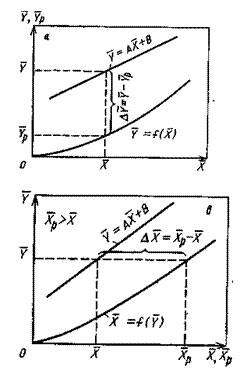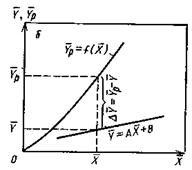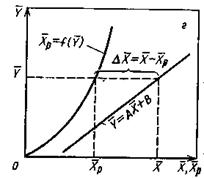Рис.1.4. Движущая сила массообменного процесса для участка аппарата:

а) по газовой фазе; б) по жидкой фазе.

При этом движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, либо L. В этой связи уравнения массопередачи, записанные по фазам, имеют вид:

, (4.6)

. (4.7)

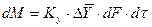
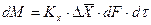
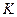
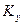
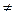
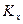
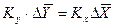
Индексы у коэффициента скорости процесса показывают, какие концентрации приняты для выражения движущей силы. В общем случае и , но всегда выполняется равенство:

. (4.8)

Из рис. 4.3. следует, что движущая сила меняется с изменением рабочих концентраций. В этой связи для всего процесса массообмена, протекающего в пределах изменения концентраций от начальных до конечных, должна быть определена средняя движущая сила по газовой фазе или жидкой — .

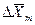
С учетом средней движущей силы процесса основное уравнение массопередачи для всей поверхности контакта фаз может быть записано в виде:

, (4.9)

. (4.10)

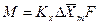
При определении движущей силы возможны два случая:

— зависимость между равновесными концентрациями не линейна и определяется функциональной зависимостью самого общего вида типа ;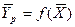

— зависимость между равновесными концентрациями линейная — 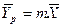( — представляет собой постоянную величину).

Определим среднюю движущую силу по фазе G для случая перехода распределяемого компонента из газовой в жидкую фазу. Для элемента поверхности имеем:

;

Из сопоставления равенств

для элементарной поверхности фазового контакта имеем

.

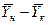
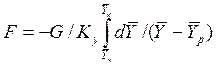
После интегрирования в пределах 0 –F и получим:

. (4.11)

Изменим границы интегрирования с целью исключения отрицательного знака перед интегралом, и вставим равенство для :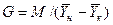

. (4.12)

При выражении движущей силы для жидкой фазы получим аналогичное выражение

(4.13)

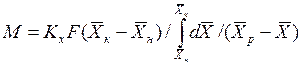
При сравнении уравнений (4.9) и (4.10) с уравнениями (4.12) и (4.13) составим выражения для средних движущих сил по газовой и жидкой фазам:

(4.14)

(4.15)

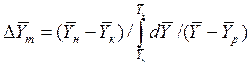
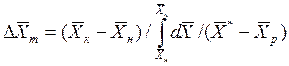
Для случаев, когда между равновесными концентрациями существует прямолинейная зависимость, при определении средней движущей силы используются более простые зависимости, вывод которых приведен в учебной литературе:

;

.

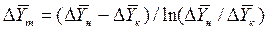
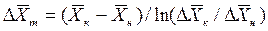
Интегралы, стоящие в правой части равенств (4.14) и (4.15), называют числами единиц переноса – сокращенно ЧЕП.

ЧЕП для газовой фазы:

.

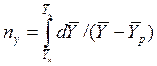
ЧЕП для жидкой фазы:

.

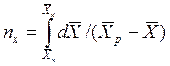
Число единиц переноса, как следует из уравнений (4.14) и (4.15), определяют по средней движущей силе:

;

.

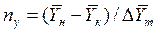
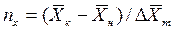
Физический смысл ЧЕП состоит в том, что эта величина характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы.

Эти соотношения справедливы для всех случаев, когда между рабочими и равновесными концентрациями существуют линейные и нелинейные зависимости.

В случае линейных зависимостей между концентрациями уравнения для вычисления ЧЕП имеют более простой вид:

;

,

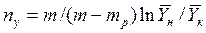
где и — тангенсы угла наклона рабочих и равновесных линий изменения концентраций.

4.1.4. Модифицированные уравнения массопередачи

В большинстве случаев основное уравнение массопередачи используют в модифицированной форме. Это в первую очередь связано со сложностью геометрического определения поверхности контакта фаз для насадочных, тарельчатых и других массообменных аппаратов.

Если поверхность фазового контакта неопределима, основной характеристикой массообменного аппарата может служить объем, высота или число ступеней фазового контакта.

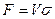
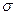
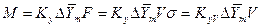
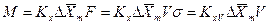
Если аппарат характеризуется объемом V, тогда , где 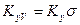(м 2 /м 3 ) — удельная поверхность фазового контакта, развиваемая в 1 м 3 объема. Модифицированные уравнения масопередачи в этом случае имеют следующий вид:

;

,

где и объемные коэффициенты массопередачи для газовой и жидкой фаз, соответственно.

Достаточно часто за основную характеристику аппарата принимают его высоту. Обозначим площадь поперечного сечения и высоту аппарата, соответственно f и H, тогда . Из уравнения (4.11) после изменения пределов интегрирования и решения относительно высоты аппарата для газовой фазы получим

.

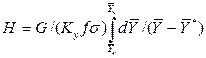
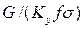
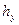
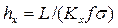
Комплекс , имеет размерность длины [м] и физический смысл, состоящий в том, что он представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП). Обозначим:

,

.

Тогда уравнения массопередачи по фазам можно записать следующим образом:

,

.

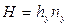
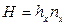
Высота, эквивалентная единице переноса, по смыслу соответствует величине, обратной объемному коэффициенту массопередачи, а число единиц переноса- величине, обратной движущей силы процесса.

Чем выше интенсивность массопередачи в аппарате, тем меньше в нем величина ВЕП. Значения ВЕП определяются по эмпирическим формулам для различных типов аппаратов. Отмети также, что ВЕП используется только для расчета аппаратов с постоянным поперечным сечением рабочей части.

Для определения ЧЕП в качестве вспомогательного приема может применяться способ определения числа ступеней изменения рабочих концентраций.

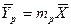
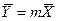
Рассмотрим процесс массопередачи, в котором зависимости между равновесными концентрациями и рабочими концентрациями распределяемого вещества представляет прямые линии и .

Если изменение рабочей концентрации распределяемого компонента в газовой фазе от входа в элемент аппарата до выхода происходит таким образом, что концентрация на выходе становится равной равновесной концентрации на входе , то такое изменение рабочих концентраций представляет собой ступень изменения концентраций (рис. 4.4).

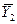
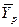
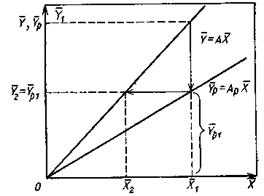Рис.4.4. Ступень изменения концентрации распределяемого компонента.

Число единиц переноса для одной такой ступени (элемента) аппарата составляет:

.

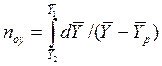
В рассматриваемом случае

и .

= .

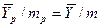
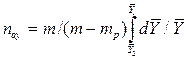
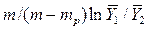
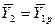
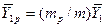
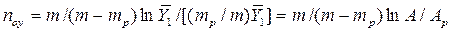
В то же время , а . И тогда

. (4.16)

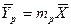
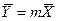
Из уравнения (4.16) следует, что только при условии прямых линий и число единиц переноса, , соответствующее одной ступени изменения концентрации, есть величина постоянная, не зависящая от концентрации.

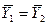
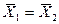
Это положение позволяет определить графическим путем общее число единиц переноса для всего аппарата. Допустим, что в процессе массообмена рабочие концентрации изменяются в пределах и (рис. 4.5).

Число ступеней изменения рабочих концентраций может быть определено графическим построением ломаной линии между равновесной и рабочей прямыми. В рассматриваемом примере число ступеней изменения концентраций (элементов) равно 4. Эта характеристика может иметь дробное значение. Общее число единиц переноса для аппарата можно определить умножением ЧЕП элемента на число элементов (ступеней контакта), т.е

.

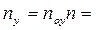
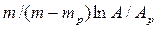
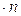
Число ступеней может быть определено и аналитически. На основе приемов аналитической геометрии (рис. 4.5,а) можно получить:

.

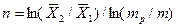
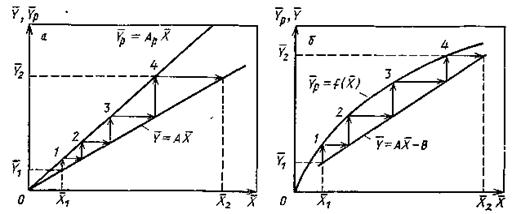Рис.1.6. Определение числа единиц переноса по числу изменения ступеней концентрации: а) равновесная и рабочая линии процесса прямые;

б) равновесная линия кривая, рабочая – прямая.

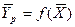
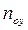
Предложенный выше путь определения ЧЕП допускается и в общем случае, когда зависимость кривая линия (рис. 4.5,б) В этом случае будет переменной величиной.

Если допустить, что в пределах одной ступени можно с некоторым приближением принять существование линейной равновесной зависимости, для определения общего ЧЕП можно предложить равенство:

.

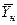
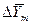
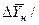
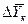
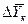
Использование этого равенства предполагает предварительное графическое определение числа ступеней изменения концентрации и графическое определение величин , , , и для каждой ступени с последующим определением общего ЧЕП. При принятой в пределах одной ступени линейной зависимости между равновесными концентрациями величина определяется как средняя логарифмическая. В подавляющем большинстве случаев ) величина может быть вычислена как средняя арифметическая.

4.1.5. Основные законы массопередачи

В процессах переноса распределяемого компонента из одной фазы в другую различают два случая: 1) перенос из потока жидкости (газа) в поток жидкости, или наоборот; 2)перенос из твердого тела в поток жидкости (газа) или в обратном направлении, т.е. массообмен между пористой твердой фазой и потоком жидкой (газообразной) фазы.

Элементарными законами, которым подчиняется перенос распределяемого вещества из одной фазы в другую, является законы молекулярной диффузии, массоотдачи и массопроводности.

Закон молекулярной диффузии (первый закон Фика). Молекулярная диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, не связанного с движением потоков жидкости. В этом случае происходит перенос молекул распределяемого компонента из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика, формулировка которого аналогична закону теплопроводности: количество вещества, продиффундировавшего в пределах фазы, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени:

, (4.16)

где — коэффициент пропорциональности, или коэффициент диффузии.

Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность 1 м 2 в течение 1 с при разности концентраций на расстоянии 1 м, равной единице.

Знак минус в правой части уравнения показывает, что при молекулярной диффузии направление перемещения вещества и градиент концентраций противоположны друг другу.

Размерность коэффициента зависит от способа выражения концентрации распределяемого компонента. Если это объемные концентрации, то размерность коэффициента следующая:

=[(кг·м·м 3 )/(м 2 ·с·кг)]=[м 2 /с].

Коэффициент диффузии не является постоянной величиной. Это достаточно малая величина для газов. Она на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления. Если в газах коэффициент диффузии не зависит от концентрации диффундирующего вещества, то в жидкостях это влияние особенно значимо для неразбавленных растворов.

Дифференциальное уравнение молекулярной диффузии
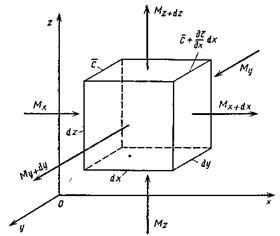
(второй закон Фика). Для вывода дифференциального уравнения, как это было принято для всех рассмотренных случаев в гидростатике и теплопроводности, выделяется в неподвижной среде элементарный параллелепипед с ребрами dx, dy, dz (рис.4.6).

Рис.4.6. К выводу дифференциального уравнения молекулярной диффузии.

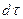
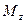
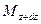
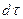
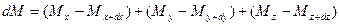
Если через этот элементарный параллелепипед за счет молекулярной диффузии перемещается распределяемое вещество, то через левую, заднюю и нижнюю грани за промежуток времени в него входят количества вещества соответственно и , а через противоположные грани – правую, переднюю, и верхнюю – входят количества вещества соответственно и . Следовательно элемент за промежуток времени приобретает диффундирующее вещество в количестве:

.

При этом концентрация диффундирующего вещества повышается на .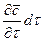

Согласно основному молекулярной диффузии, ,

.

;

;

.

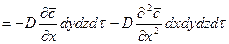
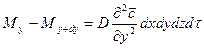
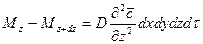
Суммируя левые и правые части трех последних равенств, получим:

.

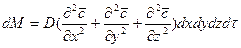
С другой стороны, тот же прирост количества диффундирующего вещества в элементе можно найти умножением объема элемента на изменение концентрации за время 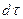, т.е.

Приравнивая правые части двух последних зависимостей, получим уравнение молекулярной диффузии:

. (4.17)

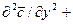
Левая часть этого уравнения характеризует локальное изменение концентрации распределяемого компонента в неподвижном элементе, выделенном в распределяющей фазе.

Закон массотдачи (Щукарева). Основной закон массоотдачи, или конвективной диффузии, впервые был сформулирован Щукаревым при изучении кинетики растворения твердых тел. Этот закон является аналогом закона теплоотдачи, сформулированным Ньютоном.

Количество вещества, перенесенного от поверхности раздела фаз в воспринимающую фазу, пропорционально разности концентраций у поверхности раздела фаз и в ядре потока воспринимающей фазы, поверхности фазового контакта и времени

, (4.18)

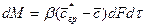
где 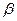— коэффициент массоотдачи, характеризующий перенос вещества в пределах фазы конвекцией и диффузией одновременно; — концентрация распределяемого компонента у поверхности раздела распределяющей фазы; — концентрация распределяемого компонента в ядре потока распределяющей фазы.

Отметим, что концентрация на границе рассматривается как равновесная концентрация.

Размерность коэффициента массоотдачи можно установить из уравнения:

[(кг·м 3 )/(м 2 ·с·кг)]=[м/с].

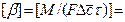
Коэффициент массотдачи показывает, какое количество вещества передается от поверхности раздела фаз в воспринимающую фазу через поверхность в 1 м 2 в течение 1 с при разности концентраций равной единице.

Для установившегося процесса коэффициент массоотдачи и концентрации сохраняют постоянное значение в рассматриваемом объеме:

. (4.19)

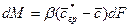
Если коэффициент массоотдачи сохраняет постоянное значение для всей поверхности, то уравнение принимает вид:

. (4.20)

Дифференциальное уравнение массоотдачи (конвективной диффузии). В основу рассмотрения явления конвективной диффузии положена теория диффузионного пограничного слоя.

Согласно этой теории распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией (рис.4.7). Рассматриваемая система состоит из двух частей: ядра и пограничного диффузионного слоя, включающего в себя достаточно тонкий ламинарный подслой. В ядре перенос вещества осуществляется преимущественно токами жидкости в условиях достаточной турбулентности. Концентрация распределяемого компонента в ядре турбулизированного потока фазы принимается постоянной.

По мере приближения к пограничному диффузионному слою турбулентный перенос затухает и с приближением к границе раздела фаз в ламинарном подслое начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого компонента, увеличивающийся по мере приближения к границе. Таким образом, область диффузионного пограничного слоя – это область проявления и роста молекулярной диффузии от малого до максимального значения.

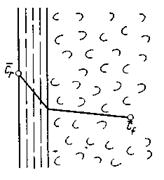Рис.4.7. К формулировке закона конвективной диффузии.

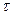
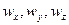
При наличии конвективной диффузии концентрация распределяемого компонента изменяется не только вследствие молекулярной диффузии, но и механического переноса его из одной области пространства в другую. В этом случае концентрация распределяемого компонента будет функцией не только координат x, y, z и времени , но и составляющих скорости перемещения частиц потока .

При конвективной диффузии бесконечно малый элемент потока перемещается из одной точки пространства в другую. В этом случае изменение концентрации распределяемого компонента может быть выражено субстанциональной производной, которая учитывает изменение ее во времени и изменения, связанные с перемещением элемента из одной точки пространства в другую:

. (4.21)

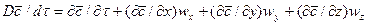
В этом равенстве 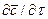представляет собой локальное изменение концентрации распределяемого компонента, а комплекс — конвективное изменение концентрации.

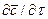
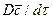
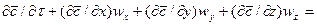
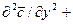
Если в уравнении молекулярной диффузии (4.17) заменить локальное изменение концентрации полным , в соответствие с уравнением (4.21), то можно получить дифференциальное уравнение конвективной диффузии:

(4.22)

Уравнение конвективной диффузии необходимо решать совместно с уравнениями движения Навье-Стокса, поскольку переменными являются концентрации и проекции скорости потока. Однако эта система уравнений не имеет аналитического решения и для получения расчетных зависимостей по массообмену приходится прибегать к теории подобия.

4.1.6. Подобие процессов переноса массы

Системы уравнений конвективной диффузии и уравнений движения не имеют общего решения. Поэтому также, как и в случае гидромеханических и теплообменных процессов, можно методами теории подобия найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде обобщенного (критериального) уравнения массоотдачи.

В это уравнение входят критерии подобия, которыми описываются подобие процессов массоотдачи на границе фазы (подобие граничных условий) и в основной массе (ядре) фазы.

Подобие граничных условий можно установить, допуская наличие пограничного слоя, в котором перенос осуществляется только молекулярной диффузией. Количество вещества, переходящего из ядра к границе фазы, составляет

.

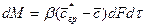
То же количество вещества переносится молекулярной диффузией через пограничный слой

.

Приравнивая выражения и проведя сокращения, получим зависимость, характеризующую подобие условий переноса на границе фазы:

.

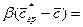
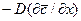
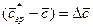
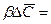
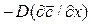
Обозначив , запишем это уравнение в виде:

.

Из этого уравнения делением левой на правую часть, сократив подобные члены и опустив знак минус, получим безразмерный комплекс, который для подобных систем является одинаковым (одним и тем же), т.е. .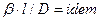

Данный комплекс величин, при выражении их в единицах одной системы, является безразмерным и в соответствии с первой теоремой подобия представляет собой критерий подобия. Этот комплекс называют диффузионным критерием Нуссельта

.

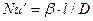
Диффузионный критерий Нуссельта выражает отношение интенсивности переноса вещества в ядре фазы к интенсивности переноса в диффузионном пограничном подслое, где массообмен определяется молекулярной диффузией.

Из дифференциального уравнения конвективной диффузии

……,

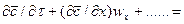
получаем безразмерные комплексы делением всех членов уравнения на :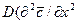

/ ; .

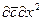
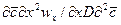
Вычеркнув в полученных комплексах символы дифференцирования и направления, после сокращения получим диффузионный критерий Фурье:

или, чтобы исключить математические действия с малыми величинами в виде

,

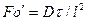
и диффузионный критерийПекле

.

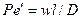
Равенство критериев 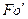в сходственных точках подобных систем – необходимое условие подобия неустановившихся процессов массоотдачи. Это равенство характеризует постоянство отношения изменения концентрации во времени к изменению концентрации вследствие чисто молекулярного переноса.

Критерий выражает меру отношения массы вещества, перемещаемой путем конвективного переноса и молекулярной диффузии, в сходственных точках подобных систем.

Подобие распределения концентраций и одновременно подобие скоростей в потоках соблюдается в общем случае в геометрически подобных системах при следующих условиях:

; ; .

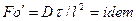
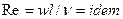
Во многих случаях вместо критерия используют отношение критериев и , которое представляет собой диффузионный критерий Прандтля:

.

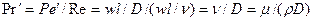
В критерий входят только величины, отражающие физические свойства потока. Этот критерий характеризует постоянство отношения физических свойств жидкости (газа) в сходственных точках подобных потоков. Критерий Прандтля рассматривается как мера подобия профилей скорости и концентрации в процессах массоотдачи.

При 1 толщина диффузионного подслоя равна толщине гидродинамического ламинарного подслоя.

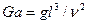
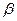
Необходимой предпосылкой подобия процессов массоотдачи является соблюдение гидродинамического подобия, которое требует, чтобы в сходственных точках подобных потоков были равны не только критерии Рейнольдса, но и критерии Фруда. Критерий Фруда часто бывает удобно заменить критерием Галилея ( ) или Грасгофа ( , где — коэффициент объемного расширения), в которые не входит скорость потока.

Определяемой величиной при расчете массоотдачи является коэффициент 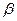, величину которого находят из диффузионного критерия Нуссельта. Этот критерий является определяемым.

Полученные критерии подобия дают возможность найти уравнение подобия конвективной диффузии:

,

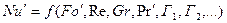
где Г₁, Г₂, …Г_n – симплексы геометрическое подобие систем, представляющие отношения характерных геометрических размеров l₁ , l₂ , …l_n к некоторому определяющему размеру l₀ .

Применительно к конкретным задачам массообмена общее уравнение подобия может быть упрощено. При рассмотрении стационарных процессов из уравнения исключается критерий Фурье

.

При вынужденном движении можно пренебречь естественной конвекцией

или .

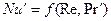
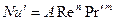
В условиях естественной конвекции

или .

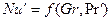
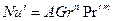
Расчетные зависимости называются критериальными уравнениями массоотдачи. Численные значения входящих в них постоянных коэффициентов A и показателей степеней n и m устанавливают при обработке опытных данных.

4.1.7. Связь коэффициентов массопередачи и массоотдачи

Чтобы установить аналиттческую зависимость между коэффициентами массопередачи и массоотдачи, принимают, что на границе раздела фаз достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу вещества через границу раздела фаз можно пренебречь. Отсюда как следствие вытекает положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок к расчету коэффициента массопередачи.

Допустим, что распределяемый компонент переходит из фазы G в фазу L и движущая сила выражается в концентрациях фазы G. При установившемся процессе массопередачи количество вещества, переходящее из одной фазы в другую фазу, определяется по уравнению:

.

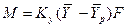
Для упрощения рассмотрим случай, когда равновесная зависимость между равновесными концентрациями представляют линейную зависимость 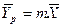, где m – тангенс угла наклона линии равновесия.

Из уравнения равновесия следует

и .

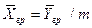
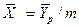
Уравнение массоотдачи для жидкой фазы

.

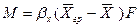
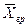
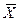
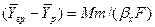
Подставляя значения и в уравнение массоотдачи, получим

. (4.23)

Из уравнения массоотдачи для газовой фазы

. (4.24)

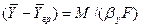
Складывая выражения (4.23) и (4.24) и исключая неизвестную концентрацию на границе раздела фаз получим

.

Из уравнения массопередачи следует, что

.

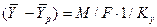
Приравнивая правые части и, сокращая подобные члены, получим выражение для коэффициента массопередачи по газовой фазе

. (4.25)

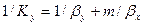
При выражении коэффициента массопередачи в концентрациях жидкой фазы получим

. (4.26)

Левые части уравнений представляют собой общее сопротивление переносу вещества из фазы в фазу, т.е. сопротивление массопередаче, а правые части – сумму сопротивлений массоотдаче в фазах. Поэтому эти зависимости являются уравнениями аддитивности фазовых сопротивлений. Эти уравнения справедливы и для случая, если линия равновесия является кривой.

4.1.8. Массопередача с твердой фазой

В основе таких распространенных процессов пищевых производств как адсорбция, сушка, экстракция из твердых пористых материалов, лежат общие закономерности массообмена с участием твердой фазы.

Массопередача между твердой и движущейся жидкой (газовой) фазой складывается из двух процесов: 1) перемещением распределяемого компонета внутри пор твердого тела к поверхности раздела фаз (или от нее) вследствие внутренней массоотдачи, или массопроводности; 2) перенос того же вещества от поверхности раздела фаз в поток жидкости (газа, пара) за счет массоотдачи. Иными словами, массопередача является результатом внутренней и внешней диффузии.

В качестве закона, которому подчиняется кинетика переноса распределяемого вещества в твердом теле, принят закон, аналогичный закону теплопроводности: количество вещества, переместившегося в твердой фазе за счет массопроводности, пропорционально градиенту концентрации, площади, перпендикулярной направлению потока вещества, и времени, т.е.

.

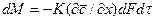
В этом уравнении коэффициент скорости процесса 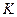называется коэффициентом массопроводности. Коэффициент массоопроводности аналогичен коэффициенту диффузии, но при одинаковых условиях меньше его, поэтому его иногда называют коэффициентом «стесненной диффузии».

Процесс перемещения вещества внутри твердого тела может быть описан дифференциальным уравнением массопроводности:

. (4.27)

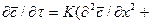
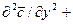
Вполне очевидно, что 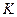не является постоянной величиной. Он зависит от природы процесса (адсорбция, сушка, выщелачивание), от ряда факторов, определяющих значение коэффициента молекулярной диффузии, и от структуры твердого пористого тела.

Дифференциальное уравнение массопроводности должно быть дополнено уравнением, характеризующим условия на границе раздела твердой и жидкой фаз. К элементарной площадке на границе раздела подводится вещество из твердой фазы в количестве

.

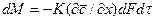
От элементарной площадки в омывающую фазу отводится

. (4.28)

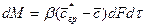
Приравнивая правые части этих уравнений, получим дифференциальное уравнение, характеризующие условия на границе раздела фаз:

. (4.29)

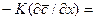
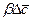
Из уравнения (1.29) может быть получен безразмерный комплекс делением правой на левую часть, который называется диффузионным критерием Био

.

Критерий Био выражает отношение интенсивности переноса вещества в ядре омывающей фазы к интенсивности переноса в твердом материале, где массообмен связан с массопроводностью.

Из дифференциального уравнения массопроводности

получаем безразмерный комплекс делением правой на левую часть, который называется диффузионным критерием Фурье

,

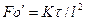
характеризующим изменение скорости потока вещества, перемещаемого массопроводностью в твердом теле.

Дифференциальное уравнение массопроводности для одномерного перемещения вещества по толщине пластины (рис.4.8) имеет аналитическое решение в виде:

, (4.30)

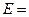
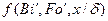
где — безразмерная концентрация распределяемого вещества в твердой фазе с координатой ; — текущая концентрация в точке в момент времени ; — определяющий размер твердого тела; безразмерная координата точки, в которой концентрация равна .

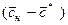
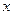
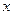
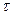
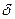
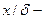
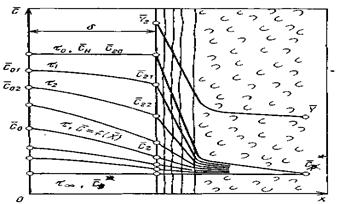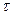
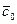
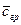
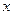
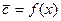
В рассматриваемом случае в момент времени концентрация внутри пластины меняется от до , в зависимости от координаты , т.е. .

Рис.4.8. Осесимметричное изменение концентрации распределяемого компонента по толщине пористой твердой пластины во времени.

📸 Видео

Массопередача лекция 3Скачать

Механизмы массопереносаСкачать

Массообменные процессы. Часть 1. Уровень: начальныйСкачать

Массообменные процессы. Часть 2. Уровень: базовыйСкачать

Урок 101 (осн). Связь коэффициентов линейного и объемного расширенияСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Подобие процессов конвективного теплообменаСкачать

Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Теплоотдача и теплопередача.Скачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Урок 94. Вычисление моментов инерции телСкачать

Урок 455. Уравнение ШрёдингераСкачать

Л1 - Теплопроводность. Закон Фурье.Скачать

Закон БернуллиСкачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

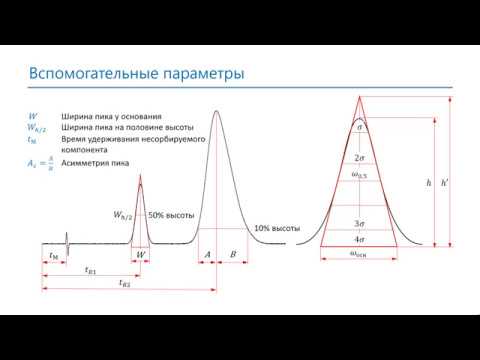
Хроматография. Основные параметрыСкачать

Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать