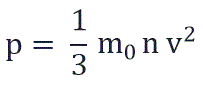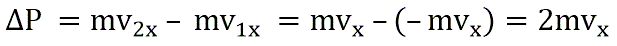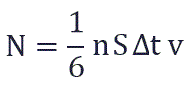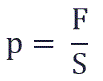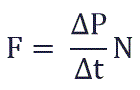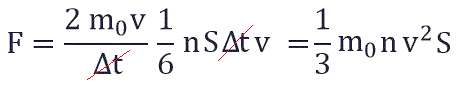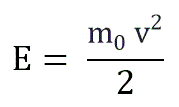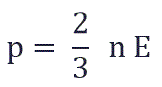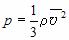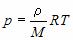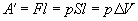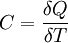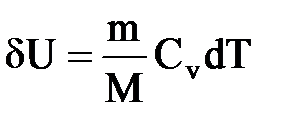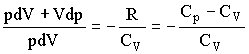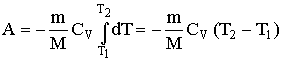Основное уравнение кинетической энергии газов его вывод

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Основное уравнение молекулярно-кинетической теории (МКТ) с выводом

В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.

Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ — разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:

• молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
• при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания

Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Основное уравнение молекулярно-кинетической теории

Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа — это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:

p – давление молекул газа на границы емкости,

m₀ – масса одной молекулы,

n — концентрация молекул, число частиц N в единице объема V;

v 2 — средне квадратичная скорость молекул.

Видео:Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Вывод основного уравнения МКТ

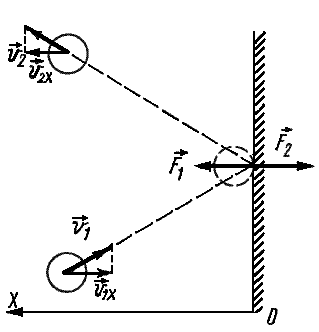
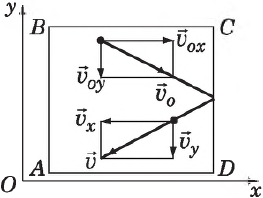
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция v_x скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:

Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv_1x = –mv_x на mv_2x = mv_x.

Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:

Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:

S – площадь этой стенки

n — концентрация частиц

Давление p равно отношению силы F к площади S, на которую действует эта сила:

Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:

Исходя из вышенаписанного получаем:

Если заменить среднее значение кинетической энергии поступательного движения молекул — E:

и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:

Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.

Понравилась статья, расскажите о ней друзьям:

Видео:Молекулярно-кинетическая теория | ЕГЭ по физике 2023 | Снежа Планк из ВебиумСкачать

Вывод уравнения молекулярно-кинетической теории идеальных газов для давления и его сравнения с уравнением Клайперона-Менделеева.

Основное уравнение молекулярно-кинетической теории идеального газа

Это уравнение связывает макропараметры системы – давление p и концентрацию молекул 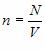с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:

Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки.

Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой.

Учитывая связь между концентрацией молекул в газе и его плотностью ( = nm₀), можно получить еще одну форму основного уравнения МКТ идеального газа:

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)

В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния:

где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная, , где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:

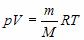
Пользуясь уравнением состояния, можно выразить один параметр через другой и построить график первого из них, как функции второго.

Графики зависимости одного параметра от другого, построенные при фиксированных температуре, объеме и давлении, называют соответственно изотермой, изохорой и изобарой.

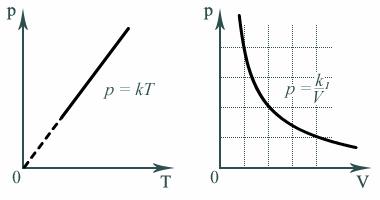
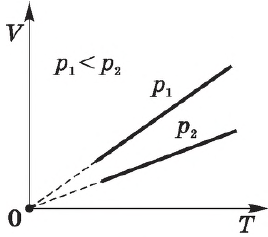
Например, зависимость давления p от температуры T при постоянном объеме V и постоянной массе m газа – это функция 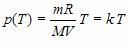, где k – постоянный числовой множитель. Графиком такой функции в координатах p,Т будет прямая, идущая от начала координат, как и графиком функции y(x)=kx в координатах y,x (рис. 3).

Зависимость давления p от объема V при постоянной массе m газа и температуре T выражается так:

,

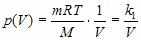
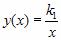
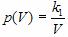
где k₁ – постоянный числовой множитель. График функции в координатах y,x представляет собой гиперболу, так же как и график функции в координатах p,V.

Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Число степеней свободы. Закон равномерного распределения энергии по степеням свободы молекул.

Температура, как мера средней кинетической энергии молекул

Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ.

Введем понятие средней кинетической энергии молекул:

(1)

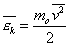
Преобразуем основное уравнение МКТ с учетом формулы (1):

т.е. основное уравнение МКТ запишем так (2)

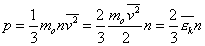
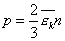
Воспользуемся уравнением К.-М. в таком виде:

(3)

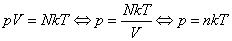
Сравним уравнения (2) и (3) и получим, что

или (4)

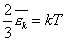
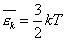
Как понимать формулу (4)?

Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура — мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества.

Молекулярно – кинетическое толкование абсолютной температуры.

C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия хаотического движения молекул (T

Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой =3/2kT где k — постоянная Больцмана, k=1.38*10 -23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы.

Формула позволяет выяснить смысл абсолютного нуля: T=0, если =0. Т. е. абсолютный нуль — это температура, при которой прекращается всякое хаотическое движение молекул.

Число степени свободы молекул. Закон равномерного распространения энергии по степеням свободы молекул.

Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.

показаны о дноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3). Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.

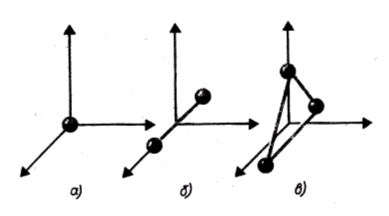
Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 — поступательного и 3 — вращательного движения (i = 6).

В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна =i/2kT В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна =i/2kT

закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией потому, что на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы =i/2kT, где i — сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=i_пост +i_вращ+2i_колеб.

В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.

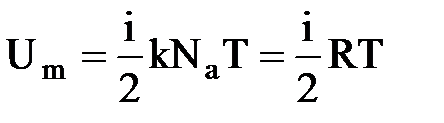
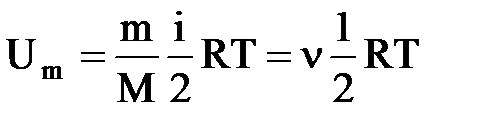
Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю, то внутренняя энергия, отнесенная к одному молю газа, равна сумме кинетических энергий NA молекул: .Внутренняя энергия для произвольной массы m газа , где k — постоянная Больцмана,  -количество вещества.

Функция распределения Максвелла – Больцмана характеризует распределение молекул по полным энергиям

38.Работа газа при изменении его объёма. Количество теплоты. Теплоёмкость. Первое начало термодинамики.

Работа газа при изменении его объёма. Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.

Если при изобарном расширении газа от объема V₁ до объема V₂ происходит перемещение поршня в цилиндре на расстояние l , то работа A’, совершенная газом, равна

где p — давление газа, 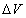— изменение его объема.

Количество теплоты — мера энергии, переходящей от одного тела к другому в данном процессе. Количество теплоты является одной из основных термодинамических величин.

Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.

Q=cmΔt, где Q- полученная телом теплота, c- удельная теплоемкость тела, Дж/(кг°С), m- масса тела, кг, Δt-изменение температуры тела, °С

Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT:

Единица измерения теплоёмкости в системе СИ — Дж/К.

Удельная теплоёмкость вещества — теплоёмкость единицы массы данного вещества. Единицы измерения — Дж/(кг К).

Молярная теплоёмкость вещества — теплоёмкость 1 моля данного вещества. Единицы измерения — Дж/(моль К).

Если же говорить про теплоёмкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоёмкость есть отношение малого приращения количества теплоты Q к малому изменению температуры T:

Первое начало термодинамики.

Первое начало термодинамики представляет собой обобщение опытных фактов и является по сути дела законом сохранения энергии, примененным к тепловым явлениям. Первое начало термодинамики имеет несколько формулировок. Одна из формулировок гласит: количество теплоты, переданное системе, идет на изменение внутренней энергии и на совершение системой работы над внешними телами, т. е. Q=∆U+A. В этом уравнении изменение внутренней энергии, Количество теплоты может быть положительным (Q>0), если тело получает теплоту, и отрицательным (Q>0), если тело отдает теплоту.

В дифференциальной форме это запишется следующим образом δQ=dU+δA

где dU и δA Первое начало термодинамики показывает, что теплоту можно преобразовывать в работу, т. е. выделять из неупорядоченного движения упорядоченное. Устройство, в котором теплота превращается в работу, называется тепловой машиной.

39.Приминение первого начала термодинамики к изопроцессам и адиабатному процессу идеального газа. Зависимость теплоёмкости идеального газа от вида процесса.

Первое начало термодинамики и изопроцессы.

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат, где процесс 1-2 есть изохорное нагревание, а 1-3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е.

Для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Q=dU

DUm=CvdT. Тогда для произвольной массы газа получим Q=dU=mC_vT/M

Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V1 до V2 равна

и определяется площадью прямоугольника. Если использовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то

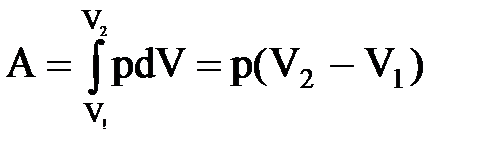
Тогда выражение для работы изобарного расширения примет вид

A=m/MR(T2-T1). Из этого выражения вытекает физический смысл молярной газовой постоянной R: если Т2-T1 =1 К, то для 1 моля газа R=А, т.е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой m количества теплоты

его внутренняя энергия возрастает на величину

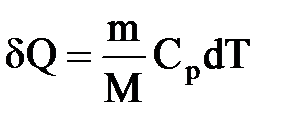
Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля — Мариотта: PV=const.

Диаграмма этого процесса (изотерма)в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Работа изотермического расширения газа:

.

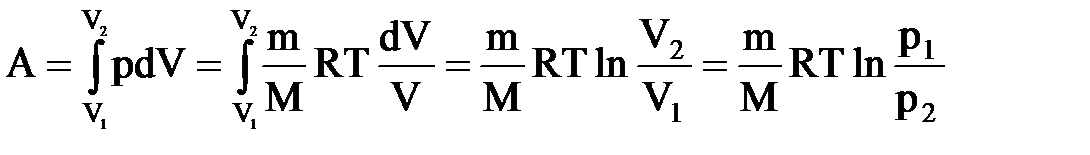
Так как при T=const внутренняя энергия идеального газа не изменяется

то из первого начала термодинамики (Q=dU+A) следует, что для изотермического процесса Q=A, т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил Следовательно, для того, чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

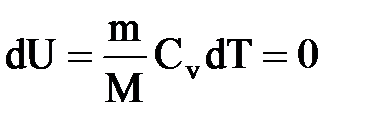
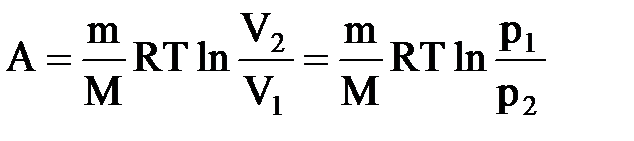
Первое начало термодинамики и адиабатический процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ = 0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики d Q = dU + dA для адиабатического процесса следует, что d A = – dU * т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя выражения для элементарной работы и приращения внутренней энергии, для произвольной массы газа получаем уравнение в виде pdV=-m/MC_vdT Продифференцировав уравнение состояния для идеального газа pV=m/MRT, получим pdV+Vdp=m/mRdT Исключив из уравнений температуру Т:

Разделив переменные и учитывая, что Cp/Cv = g , найдем dp/p=-γdV/V

Интегрируя это уравнение в пределах от р1 до р2 и соответственно от V1 до V2, а

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из полученного уравнения с помощью уравнения Клапейрона -Менделеева

соответственно давление или объем:TV γ-1 = const T γ V 1-γ = const

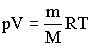
Выражения представляют собой уравнения адиабатического процесса. В этих уравнениях 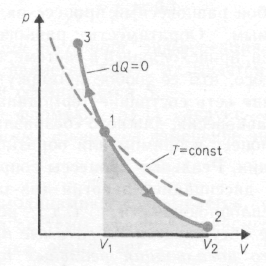безразмерная величина g = Cp/Cv = (i + 2)/I называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i = 3, g = 1,67. Для двухатомных газов (Н2, N2, О2 и др.) i=5, g =1,4. Значения g , вычисленные по формуле (g = (i + 2)/i), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой. На рисунке видно, что адиабата (pVg = const) более крутая, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1 — 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры в адиабатическом процессе. Запишем уравнение первое начало термодинамик для адиабатического процесса dA = – dU в виде

Если газ адиабатически расширяется от объема Vl до V2, то его температура уменьшается от Т1 до Т2 и работа расширения идеального газа равна

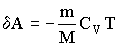
Работа, совершаемая газом при адиабатическом расширении 1 – 2 (численно равная площади под кривой), меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Видео:Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Изопроцессы, работа в термодинамике, первый закон термодинамики

Видео:Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Теория к заданию 8 из ЕГЭ по физике

Основное уравнение МКТ (давление газа)

Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.

Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.

Определим давление газа на стенку площадью $S$ сосуда $ABCD$.

Каждая молекула массой $m_0$, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс $2m_υ_x$, где $υ_x$ — проекция скорости молекулы $υ↖$ на ось $О_х$, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен $2m_υ_Z$, где $Z$ — число таких столкновений (за $1$ с) всех молекул. Очевидно, что $Z=n=/$, где $n$ — концентрация молекул в единице объема; $N$ — число всех молекул. Число $Z$ пропорционально также скорости молекул $υ_x$ и площади стенки $S:Z∼nυ_S$. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости $υ_x$, только половина движется в сторону стенки $CD$ вторая половина — в сторону $АВ$ (т. е. в обратную). Поэтому $Z=/nυ_S$, а полный импульс, переданный стенке за $1$ с, равен $2m_nυ_x^S$. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе $F=/$, то $F=m_nυ_x^S$. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить: $F↖=<m_nυ_x^S>↖$.

Сила эта зависит, таким образом, от среднего квадрата скорости $<υ_x^>↖$.

Поскольку вследствие хаотичности движения все направления равноправны, то

С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:

Усредняя это выражение по всем молекулам и учитывая $υ^2=υ_x^+υ_y^+υ_z^$, получим:

С учетом последней формулы $F↖=/m_n↖$

Следовательно, давление на стенку сосуда равно:

Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.

Уравнение $p=/=/m_n↖$ позволяет получить связь между давлением и средней кинетической энергией молекул $↖=<m_↖>/:$

Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).

Абсолютная температура

Согласно основному уравнению МКТ, давление $р$ прямо пропорционально средней кинетической энергии $E↖$ поступательного движения молекул:

где $n$ — объемная концентрация молекул. Заменив в $p=/n↖$ $n$ отношением числа молекул $N$ к объему газа $V(n=/)$, получим:

В состоянии теплового равновесия при постоянном объеме средняя кинетическая энергия данной массы газа должна иметь вполне определенное значение, как и температура. Согласно формуле $/=/↖$, это означает, что отношение $/$ для данной температуры должно быть одним и тем же для любых идеальных газов. То, что это действительно так, было подтверждено экспериментально для разных газов, находящихся в условиях теплового равновесия при постоянном объеме (измерялось давление).

Таким образом, величина $Θ=/$, которую, в отличие от микропараметра $↖$, легко измерить, является вполне однозначной характеристикой теплового состояния газа, как и температура. Измеряется $Θ$ (как и энергия) в джоулях. Зависит она только от температуры и может рассматриваться как естественная мера температуры. Однако в силу укоренившейся привычки измерять температуру в градусах был введен коэффициент пропорциональности $k$ между температурой $Θ$, выраженной в энергетических единицах, и температурой $Т$, выраженной в градусах:

Температура $Т$, определяемая равенством $Θ=kT$, называется абсолютной температурой.

Значения температуры, определенной по формуле $/=/↖$, всегда положительны в силу положительности $Θ=/$ (ни давление, ни объем, ни число частиц отрицательными быть не могут). Поэтому минимальным значением температуры является нуль. Температура может равняться нулю, если давление либо объем равны нулю. Из принятого определения температуры следует, что нулем температуры является температура, при которой прекращается хаотическое движение молекул. Она называется абсолютным нулем температуры.

Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.

Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.

Единица абсолютной температуры является одной из семи основных единиц СИ и измеряется в кельвинах (обозначается буквой $К$).

Связь между температурами, измеренными по шкалам Цельсия $t$ и Кельвина $Т$, описывается формулой:

Абсолютный нуль равен $-273.15°$С. Как правило, при расчетах пользуются округленным значением абсолютного нуля ($-273°$С).

Коэффициент пропорциональности к в формуле $Θ=kT$ называется постоянной Больцмана в честь Л. Больцмана — одного из основателей молекулярно-кинетической теории газа. Этот коэффициент составляет $k=1.38^$ Дж/К.

Постоянная Больцмана связывает температуру $Θ$ в энергетических единицах с температурой $Т$ в кельвинах. Это одна из наиболее важных постоянных в молекулярно-кинетической теории.

Температура как мера кинетической энергии

Из основного уравнения молекулярно-кинетической теории, записанного в форме $p=/↖$

и определения абсолютной температуры согласно $/=kt$

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.

Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.

Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.

Уравнение $р = nkТ$

Из формулы $p=/n↖$ может быть получена зависимость давления газа от абсолютной температуры $Т$ и концентрации его молекул, если воспользоваться выражением для средней кинетической энергии:

где $k$ — постоянная Больцмана.

Из формулы $p=nkT$ очевидно, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова.

Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Средняя скорость теплового движения молекул может быть также выражена через абсолютную температуру, если в формуле $E↖=/kT$ заменить $E↖$ на $<m_↖>/$:

Квадратный корень из этой величины называется средней квадратичной скоростью:

Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)

Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением $р$, объемом $V$ и абсолютной температурой $Т$, определяющими его состояние:

где $В$ зависит от массы газа $m$ и его молекулярной массы $М$. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.

В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: $pV=RT$, где $R$ — универсальная газовая постоянная. Если молярная масса газа $М$, то

Уравнение состояния в форме $pV=/RT$ называется уравнением Клапейрона-Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля—Мариотта, Авогадро, Шарля.

Уравнение состояния $pV=/RT$ может быть получено из зависимости давления от температуры $p=nkT$, если в нее подставить концентрацию молекул $n$ из выражения

где $N_А$ — постоянная Авогадро, $N$ — число молекул в теле.

В результате получим:

Внутренняя энергия идеального одноатомного газа

Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома $E↖=/kT$ на число атомов $N=/N_A$.

Учитывая, что $kN_A=R$, получим значение внутренней энергии идеального газа:

Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.

Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:

Следует отметить, что, согласно выражению для средней кинетической энергии одного атома $(E↖=/kT)$ и в силу хаотичности движения, на каждое из трех возможных направлении движения или каждую степень свободы по оси $X,Y$ и $Z$ приходится одинаковая энергия $/$.

Число степеней свободы — это число возможных независимых направлений движения молекулы.

Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трем направлениям, поэтому общее число возможных направлений движения — $6$. За счет связи между молекулами число степеней свободы уменьшается на одну, поэтому число степеней свободы для двухатомной молекулы равно пяти.

Средняя кинетическая энергия двухатомной молекулы равна $/kT$. Соответственно внутренняя энергия идеального двухатомного газа равна:

Формулы для внутренней энергии идеального газа можно обобщить:

где $i$ — число степеней свободы молекул газа ($i = 3$ для одноатомного и $i=5$ для двухатомного газа).

Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).

Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).

Изопроцессы в газах

Изопроцессами называются процессы, протекающие при неизменном значении одного из параметров: давления ($р$), объема ($V$), температуры ($Т$).

В идеальном газе эти процессы подчиняются газовым законам.

Газовыми законами называются количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра.

Закон Бойля-Мариотта

Закон Бойля-Мариотта — один из основных газовых законов, он описывает изотермические процессы в газе.

Процесс изменения состояния термодинамической системы при постоянной температуре называется изотермическим.

Для данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.

$pV=const$ при $T=const$

Этот закон был экспериментально открыт английским ученым Р. Бойлем в 1662 г., в 1676 г. его сформулировал также французский ученый Э. Мариотт.

Закон строго выполняется только для идеальных газов. Для реальных газов он выполняется достаточно хорошо при небольших давлениях и высоких температурах. Так, при давлении $100$ атм. и температуре $0°$С отклонение измеренного значения $рV$ от расчетного составляет $7%$. Закон Бойля-Мариотта, как и другие газовые законы, является следствием уравнения состояния идеального газа.

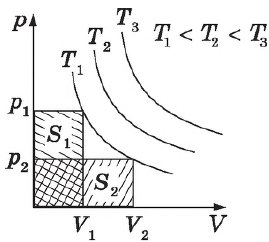
Графики зависимости $p(V)$ при $T=const$ ($p=/$) называются изотермами и представляют собой равносторонние гиперболы (площади $S_1=S_2$). Чем выше температура, тем выше лежит соответствующая ей изотерма.

Закон Шарля

Давление $p$ данной массы газа при постоянном объеме пропорционально температуре.

$p=constT$ при $T=const$

Закон был открыт французским физиком Ж. Шарлем в 1787 году.

Процесс изменения состояния термодинамической системы при постоянном объеме называется изохорным (от греч. hora — пространство).

Закон Шарля, как и другие газовые законы, является следствием уравнения состояния идеального газа:

Согласно $

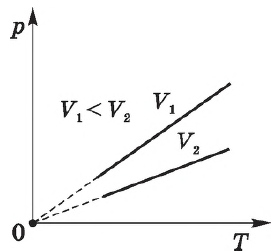
/=const$ при $V=const$, давление газа линейно зависит от температуры при постоянном объеме. Эта зависимость изображается прямой, которая называется изохорой. С ростом объема газа при постоянной температуре давление его, согласно закону Бойля—Мариотта, падает. Поэтому изохора, соответствующая большему объему, лежит ниже изохоры, соответствующей меньшему объему.

В соответствии с $

/=const$ при $V=const$, все изохоры начинаются в точке $Т=0$ (давление идеального газа при абсолютном нуле равно нулю).

Изохорный процесс используется в газовых термометрах постоянного объема.

Закон Гей-Люссака

При постоянном давлении $р$ объем $V$ идеального газа меняется линейно с температурой.

где $V_0$ — начальный объем, $t$ — разность начальной и конечной температур. Коэффициент теплового расширения идеальных газов $α=(/)K^$ одинаков для всех газов.

Процесс изменения состояния термодинамической системы при постоянном давлении называется изобарным (от греч. baros — вес, тяжесть).

Закон открыт французским ученым Ж. Гей-Люссаком в 1802 г. и независимо от него Дж. Дальтоном в 1801 г.

Закон Гей-Люссака, как и другие газовые законы, является следствием уравнения состояния идеального газа. Это становится очевидным, если в $V=V_0(1+αt)$ заменить $t$ абсолютной температурой $T=t+273.15$, а коэффициент расширения $α$ — его численным значением $/$:

Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.

Согласно $/=const$ при $p=const$, объем газа линейно зависит от температуры при постоянном давлении:

Эта зависимость графически изображается прямой, которая называется изобарой.

Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре, согласно закону Бойля—Мариотта, уменьшается, поэтому изобара, соответствующая более высокому давлению $р_2$, лежит ниже изобары, соответствующей более низкому давлению $р_1$.

В области низких температур все изобары идеального газа сходятся в точке $Т=0$, но это не означает, что объем реального газа действительно обращается в нуль. При низких температурах все газы обращаются в жидкости, а к жидкостям уравнение состояния не применимо.

🔥 Видео

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Вывод основного уравнения молекулярно кинетической теории.Скачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. Практическая часть.10 классСкачать

Выпуск 65. Идеальный газ. Вывод основного уравнения МКТ идеального газа.Скачать

Физика. МКТ: Основное уравнение МКТ. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение состояния идеального газа. 10 класс.Скачать

Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать

Секретный вывод основного уравнения МКТСкачать

Идеальный газ. Основное уравнение МКТСкачать

Урок 139. Основные положения МКТ.Скачать