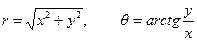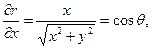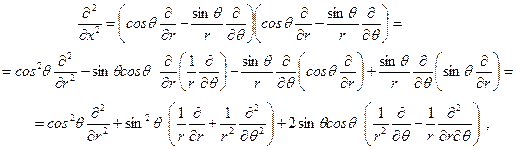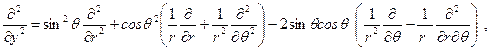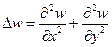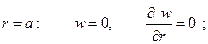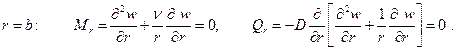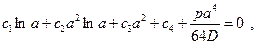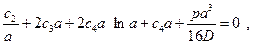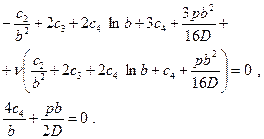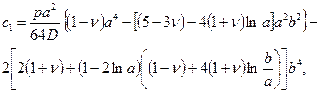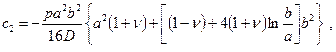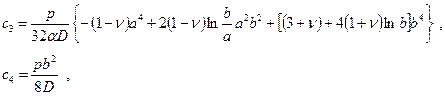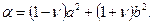| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «Прочность материалов и конструкций»
Р е ц е н з е н т ы:
доктор технических наук, профессор кафедры
«Сопротивление материалов и теория упругости»
ФГБОУ ВПО ПИМаш (ЛМЗ-ВТУЗ)
кандидат технических наук, доцент кафедры
«Прочность материалов и конструкций»
ФГБОУ ВПО ПГУПС
Изгиб пластинок: учеб. пособие / , . – СПб.: Петербургский гос. ун-т путей сообщения, 2011. – 51 с.
Приведены основы теории и примеры решения задач по изгибу эллиптических, круглых и прямоугольных пластин. При этом используются как классические аналитические методы решения указанных задач, так и аналитические методы, основанные на применении математического аппарата разрывных функций.
Предназначено для аудиторной и самостоятельной работы студентов всех форм обучения.
университет путей сообщения, 2011
В соответствии с принятым ФГОС ВПО (2011 г.) по дисциплинам сопротивление материалов, строительная механика сокращается количество часов аудиторных занятий и увеличивается время, отводимое на самостоятельную работу студентов. В связи с этим появилась необходимость в дополнительных методических материалах, позволяющих познакомиться с современными аналитическими методами расчëтов таких элементов конструкций, как пластинки.
Данное учебное пособие состоит из двух глав.
В первой главе приведены основы теории и примеры решения задач по изгибу эллиптических, круглых и прямоугольных пластин. Примеры сопровождаются теоретической и методической информацией по решению задач. Кроме того, по каждой теме приведены расчëтно-проектировочные задания для самостоятельного решения. Задачи составлены с большим числом вариантов, что обеспечивает индивидуальность исходных данных.
Во второй главе на основе математического аппарата обобщëнных функций излагается в доступной форме эффективный аналитический метод расчëта пластин на действие статических нагрузок. Рассматриваются круглые пластинки под действием равномерно распределëнной нагрузки, как по всей еë поверхности, так и кольцевой поверхности при различных условиях закрепления пластинки.
Учебное пособие предназначено для аудиторной, самостоятельной и научно-исследовательской работы студентов, изучающих сопротивление материалов и строительную механику. Рекомендуется для подготовки к самостоятельному решению задач, выполнению расчëтно-проектировочных заданий, к контрольным работам, зачетам и экзаменам в качестве дополнения к теоретическому курсу сопротивления материалов и строительной механики. Оно может быть полезно магистрам, аспирантам и стажерам.
Глава 1. Изгиб тонких пластинок
1.1 Основные понятия и гипотезы
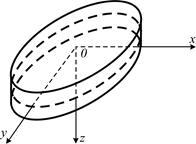
Пластины являются одним из основных конструктивных элементов многих инженерных сооружений. Под пластиной понимается тело, у которого одно измерение (высота, толщина) мало по сравнению с двумя другими размерами.
Высота (толщина) 

В прямоугольной системе координат оси 




Рис. 1.1. Пластинка: срединный слой и размеры
В зависимости от соотношения наименьшего размера основания 

• при 
• при 
• при 
В зависимости от способности деформироваться тонкие пластины делятся на жëсткие и гибкие.
Если наибольший относительный прогиб при изгибе 

Далее рассматриваются тонкие жëсткие пластинки, работающие на изгиб. Сформулируем некоторые допущения и ограничения (гипотезы), благодаря которым расчëт тонких пластин упрощается и сводится к решению линейных дифференциальных уравнений.
1. Основная гипотеза о прямых нормалях: прямолинейные отрезки, нормальные (перпендикулярные) к срединной плоскости пластины до деформации, остаются такими же и после деформации. Эта гипотеза аналогична гипотезе плоских сечений (гипотезе Бернулли), принимаемая в сопротивлении материалов при расчëте стержней.
2. Гипотеза об отсутствии поперечного давления: слои пластины, параллельные срединной плоскости, не давят друг на друга и поэтому соответствующими нормальными напряжениями сжатия 


Эти два допущения часто называют гипотезами Кирхгофа.
3. Гипотеза о вертикальном смещении точек срединной поверхности: точки срединной поверхности смещаются только в перпендикулярных к ней направлениях, то есть по направлению оси 

Вследствие принятых допущений решение задачи по определению напряжëнно-деформированного состояния (НДС), то есть по определению внутренних усилий, напряжений и перемещений в сечении пластины значительно упрощается. Задача решается в перемещениях и за основную искомую функцию принимается прогиб 
1.2 Перемещения и деформации в пластине
Будем рассматривать пластинки постоянной толщины, нагруженные поперечной распределëнной нагрузкой 


Горизонтальные перемещения точек пластины, не принадлежащие срединной плоскости, в направлении осей 








Рис. 1.2. Горизонтальное перемещение
Из рис. 1.2 видно, что перемещение 



Используя соотношения Коши, связывающие линейные деформации 







получим выражения для деформаций в пластинке




Знак минус означает, что перемещение точки при 


1.3 Напряжения и внутренние усилия в пластине
Согласно закону Гука (с учëтом принятого допущения 



где 




Из выражений (1.3) следует, что напряжения 





В соответствии с условиями статической эквивалентности внутренние моменты, возникающие в пластине, определяются следующими выражениями:



Подставляя формулы для напряжений (1.3) в соотношения (1.4), получим значения моментов, выраженные через прогиб пластинки



Здесь 



называется цилиндрической жëсткостью и является физико-геометрической характеристикой пластинки при изгибе. Цилиндрическая жëсткость пластины при изгибе отличается от обычной изгибной жëсткости балки 


Поперечные силы выражаются через моменты следующими уравнениями


Подставляя сюда соотношения (5), получаем значения поперечных сил в зависимости от прогиба пластины


Отметим особенности обозначения внутренних силовых факторов в пластинах, отличные от тех, что были приняты в балках:










Различие между поперечными силами 



Кроме того, следует принять во внимание, что изгибающие и крутящие моменты, а также поперечные силы отнесены к единице длины сечений, параллельных плоскостям 

Рис. 1.3. Напряжения и внутренние усилия в пластине
1.4 Дифференциальное уравнение изгиба пластины
Если выделить в пластинке элементарный параллелепипед и спроектировать все силы, действующие на него, на ось 

где 
Подставляя сюда выражения для поперечных сил (1.7), получим дифференциальное уравнение пластины

Уравнение (1.8) называют уравнением Софии Жермен и записывают короче так:


где 

Расчëт пластинок сводится к интегрированию уравнения (1.9) при заданной правой части (нагрузке) и определëнных граничных условиях.
1.5 Граничные условия
Задача интегрирования уравнения (1.9) заключается не только в том, чтобы найти функцию 
1) З а щ е м л ë н н ы й к р а й.
Защемление боковой грани пластинки (при 



2) Ш а р н и р н о – о п ë р т ы й к р а й.
Шарнирно-опëртая грань пластины 

В силу первого равенства, на всëм контуре 


3) С в о б о д н ы й к р а й (отсутствие опорных связей).
Кирхгофом было показано, что для определения прогиба 



Если на свободном крае пластинки приложены внешний изгибающий момент 



В случае пластины с криволинейным контуром вводится система координат, связанная с нормалью 

Ниже рассматриваются эллиптические пластинки с первым граничным условием, то есть жëсткой заделкой и круглые пластики с различными закреплениями.
1.6 Эллиптическая пластинка
Рассмотрим эллиптическую пластинку, защемлëнную по контуру и нагруженную равномерно распределëнной нагрузкой интенсивности 



где 


Это выражение и его первые производные по 



После дифференцирования находим

Выражения для изгибающих моментов 





Выделим значения моментов в характерных точках:
– на концах большой полуоси



– на концах малой полуоси



– в центре пластинки



Так как зависимость изгибающих моментов от координат имеет вид параболической функции, то для построения эпюр 

Аналогичным образом найдëм выражения для поперечных сил вдоль координатных осей, подставив функцию прогиба (1.13) в формулы (1.7):


В центре пластинки 

Наконец, подставляя 



Напряжения в центре пластинки



Пример расчëта. Рассмотрим эллиптическую пластинку, защемлëнную по контуру и нагруженную равномерно распределëнным давлением интенсивности 
Дано: давление 






1. Определить наибольший прогиб пластины (в еë середине).
2. Построить эпюры поперечных сил и изгибающих моментов по направлению главных диаметров контура.
3. В точке 



Жëсткость заданной пластинки, согласно выражению (1.6)

1) Прогиб в центре пластины (формула (1.14))

2) Величины поперечных сил 



Результаты вычислений с шагом 
Эпюры внутренних усилий 



Т а б л и ц а 1.1
Величины поперечных сил и изгибающих моментов, возникающих в эллиптической пластине




Видео:Изгиб тонких пластин (часть 1)Скачать

Вывод уравнения изгиба круглой пластины
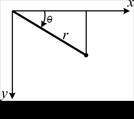
Преобразование декартовых координат к полярным осуществляется по формулам:

где 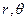
Если принять начало радиуса полярной системы совпадающим с началом оси х декартовой системы, то формулы
устанавливают связь координат произвольной точки на плоскости.
Производные величин 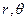
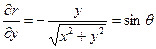
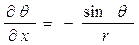
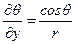
На основании данных вычислений без труда находятся производные:
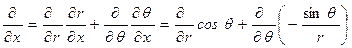
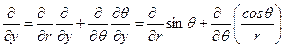
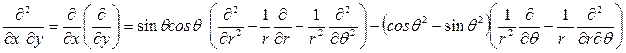
с учётом данных определений производных в полярных координатах принимает вид
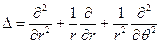
С его помощью левая часть уравнения изгиба пластинки в полярных координатах может быть представлена состоящей из сомножителей
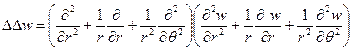
Приравнивая это выражение величине 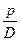
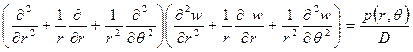
Здесь, как и для прямоугольной пластинки, 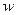
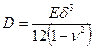
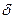
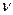
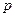
При действии симметричной нагрузки прогибы не зависят от окружной координаты. Следовательно, производные функции прогибов по 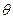
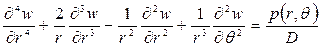
2.1 Интегрирование уравнения изгиба круглых пластин
Общий интеграл уравнения (2.7) можно представить как сумму частного решения и решения однородного уравнения при 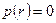
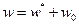
Частное решение в случае равномерно распределённой нагрузки очевидно —
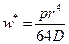
Решение однородного уравнения записывается в виде
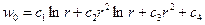
где 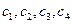
Таким образом, общее решение для круговой пластинки имеет вид
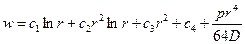
2.3. Определение изгибающих моментов и поперечных сил круглых пластин
Величины изгибающих моментов и поперечных сил в круглых пластинах, как и уравнение изогнутой поверхности, можно выразить в полярной системе. Формулы для них, во – первых, вполне естественны для анализа круглых пластин, а, во – вторых, необходимы при практическом решении задач на стадии формулировки краевых условий.
Формулы для изгибающих моментов и поперечных сил несложно вывести на основе известных выражений аналогичных величин в декартовых координатах (см. формулы для прямоугольных пластинок (1.6,а)). Воспользовавшись, например, определением
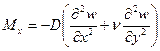
после подстановки формул преобразования производных (2.3) находят моменты в радиальном направлении
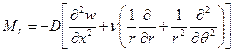
Аналогично выводят формулы и для окружных и крутящих моментов:
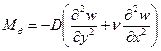
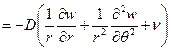
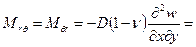
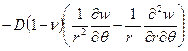
Точно также и для поперечных сил легко установить, что:
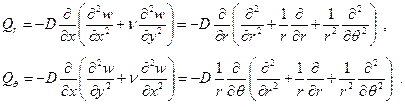
При полярно – симметричном изгибе круглой пластинки формулы упрощаются:
Изгибающие моменты равны
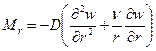
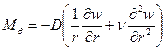
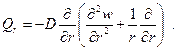
Остальные усилия не возникают совсем
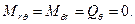
2.4. Граничные условия для круглых пластин
А) При защемлении контура
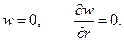
Б) При шарнирном опирании контура
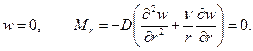
В) На свободном контуре (при отсутствии внешних воздействий по контуру отверстия)
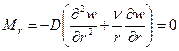
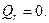
Г) На свободном контуре (при наличии внешних воздействий)
по наружному контуру
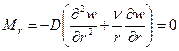
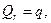
если нагрузка 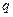
если нагрузка 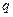
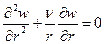
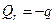
2.5. Прогибы кольцевых пластин
На основе полученного решения несложно определит прогибы не только сплошных круглых пластинок, но пластинок с симметричным отверстием, т. е. кольцевых пластинок, при самых разных краевых условиях.
В частности, для круглой пластинки с защемлённым внешним контуром и шарнирным опиранием в месте выреза (рис. 2.2) краевые условия имеют вид:
на внешнем контуре, при
на внутреннем – при
Подставив сюда выражение для прогибов (2.11), приходят к системе четырёх уравнений относительно постоянных интегрирования:
Решив систему, находят:
где
Если ещё ввести параметры:
то тогда прогибы кольцевой пластинки находят по формуле
Значения моментов в пластинке при действииравномерно распределённой нагрузки р вычисляют по формулам (2.14).
| | | следующая лекция ==> | |
| Механическая обработка. Механическая обработка. Технологические возможности способов резания | | | Происхождение, сущность, исторические типы и формы морали |
Дата добавления: 2015-12-16 ; просмотров: 1563 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:7 Цилиндрический изгиб пластиныСкачать

ПроСопромат.ру
Видео:Изгиб с кручениемСкачать

Технический портал, посвященный Сопромату и истории его создания
Видео:Сопротивление материалов. V-01 (пластины, введение).Скачать

Расчет круглых пластинок (пластин) постоянной толщины на действие осесимметричной нагрузки
Гипотезы Кирхгоффа для тонких пластинок и основные зависимости для расчета
Многие элементы конструкций, такие как днища и крышки резервуаров, аппаратов, люков и т.п., представляют собой круглые пластинки. Наиболее простой вид деформации таких элементов – их осесимметричный изгиб, который мы и будем рассматривать.
На рис.1 показано диаметральное сечение круглой пластинки и несколько осесимметричных нагрузок:
F– сосредоточенная сила в центре пластин,
T– кольцевая нагрузка,
q – распределённая нагрузка.

h – характерная толщина пластинки (она может быть постоянной, а может быть и переменной),
а – внешний радиус пластинки.
Срединная плоскость делит толщину пластинки пополам. Вертикальные линейные перемещения точек срединной плоскости (по оси z) называются прогибами и обозначаются буквой w.
Пластинка считается тонкой, если её толщина не превышает пятой части диаметра 

Для таких пластинок справедливы допущения, называемые гипотезами Кирхгоффа:
- Считается, что любой нормальныйэлемент (перпендикуляр к срединной плоскости) остается нормальным к срединной поверхности в процессе изгиба пластинки и длина его при этом не изменяется.
- Считается, что в точках срединной поверхности пластинки отсутствуют деформации растяжения, сжатия и сдвига.
- Считается, что напряжения в сечениях, параллельных срединной плоскости, пренебрежимо малы по сравнению с остальными напряжениями.
Будем различать в пластинке два направления:
1–радиальное (все параметры такого направления обозначим индексом «1»),
2–окружное (все параметры этого направления будем отмечать индексом «2»).
Рассмотрим положение в пространстве до и после изгиба пластинки двух смежных бесконечно близких точек В и В’, отстоящих от срединной плоскости на произвольном расстоянии «z» (рис.2).

В соответствии с гипотезами Кирхгоффа для радиальной и окружной деформации получаем:

Тогда из закона Гука для плоского напряжённого состояния (σ1≠0, σ2≠0, σz=0) следует:

Зависимость между прогибом (w) и углом поворота (θ) следует из рассмотрения рис. 3:
Р
А именно, 
Напряжения на гранях элемента, выделенного из пластинки двумя радиальными и двумя окружными сечениями, показаны на рис.4.

Вычислим внутренние усилия на гранях элемента, показанного на рис.4.
Нормальные напряжения σ1 группируются в изгибающий момент М1, а σ2 – в изгибающий момент М2:


Касательные напряжения, собранные с площадки единичной ширины, образуют поперечную силу в окружном сечении:
Нормальные напряжения легко выражаются через изгибающие моменты. Для этого достаточно подставить выражения (4) в (2). Тогда получаем:


Эпюры этих напряжений показаны на рис. 5.
Правило знаков изгибающего момента для круглых пластинок:
положительным будем считать изгибающий момент, соответствующий растяжению верхнего слоя пластинки.
Наконец, рассмотрим равновесие элемента пластинки под действием усилий и действующей нагрузки (рис.6)

Дифференциальное уравнение задачи и его аналитическое решение
Составим два уравнения равновесия:
1. Σz=0 , откуда, пренебрегая бесконечно малыми третьего порядка, имеем:
или, после сокращения на 
Интегрируя это уравнение, получим:
2. ΣΜt=0,откуда после сокращений найдем:
Заменив по малости 




Подстановкой в это уравнение выражений М1 и М2 по формуле (4) получим разрешающее уравнение:

Это обыкновенное линейное дифференциальное уравнение второго порядка относительно функции угла поворота θ ( r ).
Можно получить разрешающее уравнение для осесимметричного изгиба круглых пластинок и через функцию прогиба w ( r ), но оно будет иметь четвертый порядок:

Рассмотрим схему решения уравнения (7) методом Эйлера. Полное решение состоит из общего и частного решения:
Общее решение однородного уравнения по Эйлеру отыскивается с помощью подстановки:
и однородное уравнение, соответствующее (7), будет:
откуда имеем характеристическое уравнение:
Его корнями являются: α1=+1, α2=-1, и соответствующее общее решение однородного уравнения (7) будет:

где: А и В – постоянные интегрирования.
С целью отыскать частное решение неоднородного уравнения свернем его левую часть к виду:
Тогда уравнение (7) примет вид:
Дважды интегрируя, найдем:
Очевидно, что два первых слагаемых представляют общее решение, а последнее – решение частное:

Здесь: s – текущая координата (радиус) внутри интервала (r0, r).
Расчет пластинок (пластин) постоянной толщины
Пример 1. Чистый изгиб сплошной круглой пластинки моментами, распределенными по шарнирно опертому контуру.
В данном случае поперечная нагрузка отсутствует. Равна нулю и поперечная (перерезывающая) сила Q ® =0.
Поэтому частное решение (10) также равно нулю, и остается только общее решение (9). Итак,
Значения А и В следует искать из граничных условий:
— на внешнем контуре (r=a) нам известен радиальный изгибающий момент М1=m,
— в начале координат, при r=0 из соображений симметрии угол поворота должен равняться нулю: θ=0.
Подчиняя решение (9) второму условию, имеем:
откуда В=0, так как если В≠0, то θ→∞.
Тогда из первого условия найдем:

В данном случае при В=0 изгибающий момент окружного направления будет равен:
а прогиб любой точки из уравнения (3):
Постоянную «С» найдем из условия шарнирного закрепления контура (при r=a: w=0): чтобы его удовлетворить, следует положить r0=a, тогда и С=0, а
Наибольший прогиб (при r=0) составит:
Пример 2. Рассмотрим чистый изгиб кольцевой пластинки
Общее решение здесь такое же, как и в предыдущем примере, но граничные условия другие, а именно:
при r=a: М1=m,
при r=b: М1=0.
Удовлетворяя этим условиям, будем иметь:
Эпюры изгибающих моментов показаны на схеме.
Для угла поворота получим соотношение:
Найденное здесь решение для кольцевой пластинки позволяет получить расчетные формулы для кольца как частный случай.
При каких соотношениях а и b кольцевую пластинку можно считать кольцом,
сечения которого поворачиваются без изгиба срединной плоскости?
Полагая 
где 
В рассматриваемых условиях нагружения кольцо испытывает деформацию изгиба. Из условия равновесия половины кольца:
или 2Мизг=2mR, откуда Мизг=m·R.
Следовательно, в сечениях кольца возникают нормальные напряжения от изгиба:
Из рисунка кольцевой пластинки следует:
С другой стороны, из закона Гука для растяжения:
Из геометрических соображений получается тот же результат:
Пример 3. Сплошная круглая пластинка, защемлённая по внешнему контуру, находящаяся под действием равномерно распределённой нагрузки по всей её площади. Найдём усилия, перемещения, проверим прочность.
В отличие от предыдущих примеров, где на пластинку действовали краевые нагрузки, здесь придётся отыскивать частное решение неоднородного уравнения
Для определения Q (s) выделим центральную часть пластинки радиусом «s» и рассмотрим её равновесие:
Итак, полное решение будет:
Граничные условия задачи:
(1) при r=0, θ=0, откуда: В=0,
и тогда
(2) при r=а, θ=0, откуда:
Вычислим изгибающие моменты:
Для построения эпюр изгибающих моментов вычислим крайние ординаты:
Найдем прогибы:
«С» найдем из граничного условия:
при r=a, w=0, откуда:
Тогда прогиб в любой точке пластинки будет:
Наибольший прогиб в центре пластинки, при r=0:
Для оценки прочности пластинки следует найти напряжения.
В точках внешнего контура (r=a) радиальные (σ1) и окружные (σ2) нормальные напряжения у поверхности пластинки, то есть при
В центре пластинки, при r=0:
И в точках, расположенных на контуре, и в центре пластинки имеет место плоское напряженное состояние. Следовательно, оценить прочность материала можно только с помощью теорий прочности. Если материал пластинки пластичный, то рекомендуется применять третью либо четвертую теории. Так, с позиции третьей теории прочности в точках контура (при r=a),
А в центре пластинки (r=0), где
Сравнивая величины эквивалентных напряжений, заключаем, что наиболее опасной точкой пластинки является та, что расположена на контуре, и тогда условием прочности будет:
Пример 4. Рассмотрим круглую пластинку под действием сосредоточенной силы в ее центре
Задача отличается от предыдущей иным частным решением.
В данном случае:
Подставляя в формулу частного решения (10), имеем:
Тогда полное решение будет:
Найдём А и В из граничных условий:
Тогда полное решение:
Вычислим изгибающие моменты:
Эпюры моментов показаны на схеме. Они совмещены на одном графике: правая половина – эпюра М1, а левая – эпюра М2. В центре пластинки, при 
А на краю пластинки, при r=a: ℓn1=0, и тогда
Бесконечно большие значения изгибающих моментов являются лишь следствием крайней схематизации (сосредоточенная сила приложена в точке). На самом же деле такого не бывает, нагрузка распределена по некоторой малой площадке, а в малой окрестности точки приложения силы М1=М2, как и во всех других случаях загружения.
📸 Видео
Изгиб Л.4 \ ДУ изогнутой оси (метод Коши-Крылова)Скачать

Перемещения при изгибе. Часть 1. Дифференциальное уравнение изогнутой оси бруса.Скачать

Сопротивление материалов. V-04 (круглая пластина с опёртым краем, нагружена равномерным давлением).Скачать

Пример расчёта тонкой пластиныСкачать

Трёхсантиметровые волны: фазовая зонная пластинкаСкачать

Понимание напряжений в балкахСкачать

Цикл вебинаров "Механика конструкций". Тема 5Скачать

Основы сопромата | Федоров Дмитрий АлександровичСкачать

Механика конструкций. Тема 5. Теория и практика расчета пластинСкачать

Изгиб (лекция). Часть 1 Общие сведения и ВСФ при изгибеСкачать

Сопротивление материалов. V-03 (круглая пластина, заделанная по краю, под равномерным давлением).Скачать

Четвертьволновая пластинкаСкачать

Изгиб пластин (часть 3)Скачать

Сопротивление материалов. V-02 (круглая пластина с поперечной силой в центре).Скачать

Круглое отверстие. Геометрическая оптика - дифракция ФренеляСкачать

Сопротивление материалов. Лекция: изгиб балок, основные сведенияСкачать