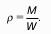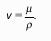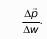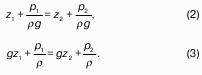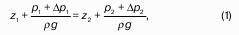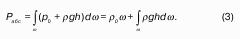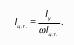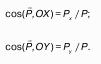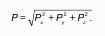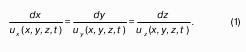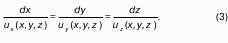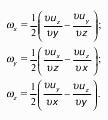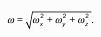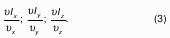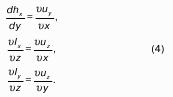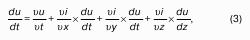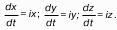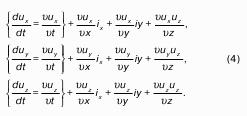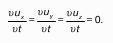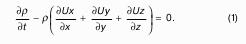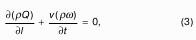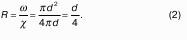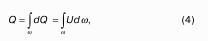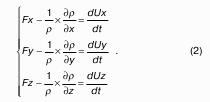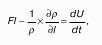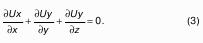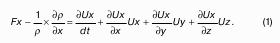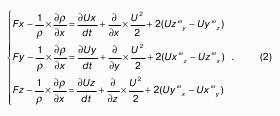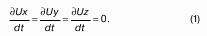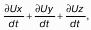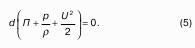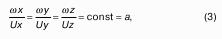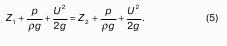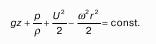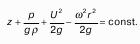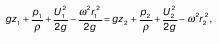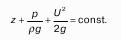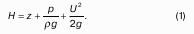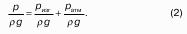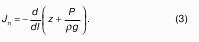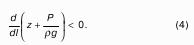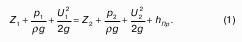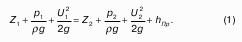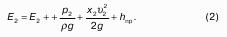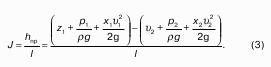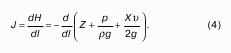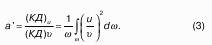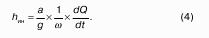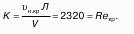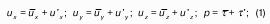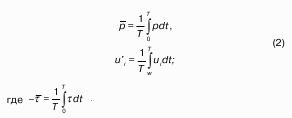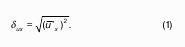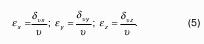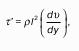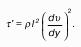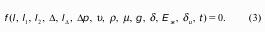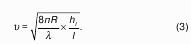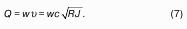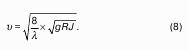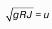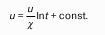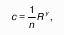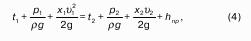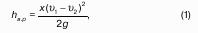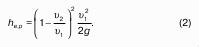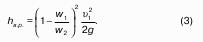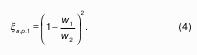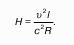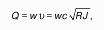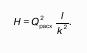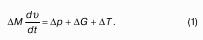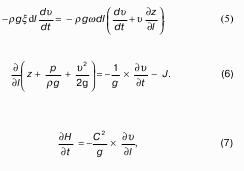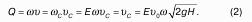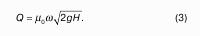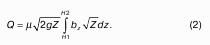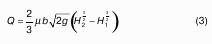Основное уравнение гидростатики учитывает следующие виды энергией

Видео:Основы гидродинамики и аэродинамики | основное уравнение гидростатики | для взрослыхСкачать

Основы гидравлики

Учебные вопросы:

Видео:Основное уравнение гидростатики (задачи)Скачать

Основные физические свойства жидкости.

В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.

Жидкости подразделяют на два вида:

Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами).

К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие

Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию.К газообразным жидкостям относятся все газы.

К основным физическим свойствам жидкости относятся:

Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.

Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.

Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях

Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.

В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.

Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.

Гидростатика

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Гидростатическое давление обладает свойствами

• Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
• Свойство 2. Гидростатическое давление неизменно во всех направлениях.
• Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.8 ) и на ее свободную поверхность действует давление P0 . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем:

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Пьезометрический и гидростатический напоры

Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине присоединены пьезометры I и II (рис. 9).

Давление на свободной поверхности в сосуде больше атмосферного. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю.

Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой. За плоскость сравнения может быть принят уровень земли, пола.

Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота.

Пьезометрическая высота – мера манометрического давления в точке А. Приведенная высота – мера абсолютного давления в точке В. Разность высот , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.

Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:

Подставив это выражение в формулу (1) получим:

это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором Hs.

В уравнении (5) Hs=const для любой точки жидкости, а не зависит от положения точки. Значит:

Поэтому, сколько бы мы пьезометров не подключили, во всех пьезометрах жидкость установится на одном уровне: плоскость, соответствующая уровню П–П, называется пьезометрической плоскостью, а уровню Н–Н – напорной плоскостью.

Пьезометрический напор является мерой удельной потенциальной энергии жидкости. Предположим, что вес частицы жидкости в точке А. равен G. о отношении к плоскости сравнения О – О запас потенциальной энергии положения равен G*z, где -Z высота от плоскости О – О до точки А.

Под действием избыточного гидростатического давления Pm частица, находящаяся на глубине h , может подняться на высоту hp, то есть она обладает потенциальной энергией давления равной G*hp. Полная потенциальная энергия частицы жидкости весом G равна G*z+G*hp.

Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:

Аналогично, гидростатический напор Hs является также мерой удельной потенциальной энергии жидкости, но большей по сравнению Hp на величину удельной потенциальной энергии атмосферного давления.

Вакуум. Закон Паскаля.

Вакуум — пространство, свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, содержащую газ при давлении значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного падения молекул газа λ и характерным размером среды d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий, средний и высокий вакуум.

Насос для демонстрации вакуума

Законом Паскаля в гидростатике называется следующее утверждение,сформулированное французским учёным Блезом Паскалем: давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические процессы и др.

В законе Паскаля речь идет не о давлениях в разных точках гидравлической системы, а о возмущениях давления в разных точках, поэтому закон справедлив и для жидкости в поле силы тяжести.

В случае движущейся несжимаемой жидкости можно условно говорить о справедливости закона Паскаля, ибо добавление произвольной постоянной величины к давлению не меняет вида уравнения движения жидкости, однако в этом случае термин закон Паскаля обычно не применяется. Для сжимаемых жидкостей (газов) закон Паскаля, вообще говоря, несправедлив.

Виды движения жидкости

Виды движения жидкости бывают:

Неустановившимся – называют движение жидкости, все или некоторые характеристики которого изменяются во времени, т. е. давление и скорость зависят как от координат , так и от времени

Примерами неустановившегося движения являются опорожнение резервуаров, водохранилищ, движение воды в реках при переменном уровне (при паводках, сбросах воды через плотину) и т. д.

сброс воды через плотину

Установившимся – наз. движение жидкости неизменное во времени, при котором давление и скорость являются функциями только координат, но не зависит от времени. u = f1(x, y, z); p = f2(x, y, z).

Установившееся движение подразделяется на:

Равномерное движение характеризуется постоянством параметров по длине потока. Примерами такого движения являются движения в трубах постоянного сечения и в каналах правильной формы. Поле линий тока равномерного движения – семейство параллельных прямых.

При неравномерном движении скорость, глубина, площади сечений потока изменяются по его длине. Из неравномерных движений можно выделить так называемое плавно изменяющееся движение, которое характеризуется малой кривизной линий тока и малым углом расхождения линий тока .

В зависимости от причин, вызывающих движение, и условий, в которых оно происходит, различают:

• напорное движение
• безнапорное движение

Напорное движение происходит в потоке, со всех сторон ограниченном твердыми стенками. Давление во всех точках потока отлично от атмосферного и может быть как больше, так и меньше последнего. Движение происходит под действием разности давлений по длине потока, которая может быть создана водонапорной башней, питающим баком, насосной установкой.

Безнапорное движение происходит под действием силы тяжести при наличии свободной поверхности жидкости. Примерами безнапорного движения является движение в реках, каналах и трубах, когда сечение последних не полностью заполнено жидкостью.

Гидродинамика

Предметом изучения гидродинамики является движущаяся жидкость. Как было указано ранее, все без исключения физические и химические процессы, которые составляют основу промышленных технологических процессов, происходят в динамических условиях, в условиях движения текучих сред.

При движении жидкостей под воздействием внешних сил в потоках прежде всего формируются поля скоростей микро- и макрочастиц, которые определяют формирование температурных и полей концентраций веществ, что в конечном итоге обусловливает скорость протекания процессов.

На движущуюся жидкость, кроме сил, которые действовали на покоящуюся жидкость (поверхностные силы гидростатического давления и массовые силы: силы тяжести и внешние силы инерции), действуют дополнительные силы инерции и силы трения. В отличие от гидростатического давления, величина которого не зависит от ориентации поверхности, на которое оно действует, возникающее при движении гидродинамическое давление благодаря развитию напряжениям сдвига (касательным силам), различно в направлении осей X, Y и Z.

Наличие сил внутреннего трения между движущимися частицами жидкости (в соответствии с законом внутреннего трения Ньютона) является первопричиной различия скоростей движения в различных точках по поперечному сечению канала. Характер этого различия, который обусловливается характером связи между давлением и скоростью движения частиц в любой точке потока. Это и является основной задачей теории гидродинамики.

Уравнение неразрывности потока.

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 15 расходы во входном и выходном сечениях напорной трубы равны: q1 = q2.

Схема к уравнению неразрывности потока.

С учётом, что q = Vw, получим уравнение неразрывности потока:

Если отсюда выразим скорость для выходного сечения:

то легко заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

Ламинарный и турбулентный режим движения жидкости.

Наблюдения показывают, что в природе существует два разных движения жидкости:

• žслоистое упорядоченное течение – ламинарное движение, при котором слои жидкости скользят друг друга, не смешиваясь между собой;
• žтурбулентное неурегулированное течение, при котором частицы жидкости движутся по сложным траекториям, и при этом происходит перемешивание жидкости.

От чего зависит характер движения жидкости, установил Рейнольдс в 1883 году путем. Эксперименты показали, что переход от ламинарного к турбулентному движению происходит при определенной скорости (критическая скорость), которая для труб различных диаметров неодинакова: при увеличении диаметра она увеличивается, критическая скорость так же увеличивается при увеличении вязкости жидкости. Рейнольдс вывел общие условия существования ламинарного и турбулентных режимов движения жидкости. По Рейнольдсу режима движения жидкости зависят от безразмерного числа, которое учитывает основные, определяющие это движение: среднюю скорость, диаметр трубы, плотность жидкости и ее абсолютную вязкость.

Это число называется числом Рейнольдса:

Число Рейнольдса, при котором происходит переход от одного режима движения жидкости в другой режим, называется критическим .

При числе Рейнольдса наблюдается ламинарный режим движения, при числе Рейнольдса – турбулентный режим движения жидкости. Чаще критическое значение числа принимают равным это значение соответствует переходу движения жидкости от турбулентного режима к ламинарного.

При переходе от ламинарного режима движения жидкости к турбулентному критическое значение имеет большее значение. Критическое значение числа Рейнольдса увеличивается в трубах, сужаются, и уменьшается в тех, что расширяются. Это объясняется тем, что при сужении поперечного сечения скорость движения частиц увеличивается, поэтому тенденция к поперечного перемещения уменьшается.

Уравнение Бернулли.

Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

p — плотность жидкости,

v— скорость потока,

h— высота, на которой находится рассматриваемый элемент жидкости,

p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

g— ускорение свободного падения.

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии .

Соотношение, близкое к приведенному выше, было получено в 1739 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Bernoulli Johann 1667-1748

СВОЙСТВА ГАЗОВ И ЖИДКОСТЕЙ

Список литературы:

ž1. В.П. Гусев «Основы гидравлики», Томск, 2009 г.

ž2. Бретшнайдер С. «Свойства газов и жидкостей», Москва

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Основы гидравлики

Видео:Гидростатическое давлениеСкачать

Гидростатика и ее законы

Гидростатика – раздел гидравлики, в котором изучаются законы равновесия жидкостей, находящихся в покое.

Понятие покоя или равновесного состояния по отношению к жидкости можно отождествлять с аналогичным понятием в одном из разделов технической механики — статике. Любое тело, материальная точка или обособленный объем вещества (в т. ч. жидкости) считается покоящимся, если все силы (внешние и реактивные), действующие на этот материально существующий субъект (т. е. имеющий массу), уравновешивают друг друга.

Тем не менее, жидкость по своим свойствам и «способностям» уникальна, поэтому гидростатика призвана пояснить некоторые особенности поведения жидкого вещества в тех или иных условиях.

Гидростатическое давление

На жидкость, находящуюся в покое действуют массовые и поверхностные силы. Массовыми являются силы, действующие на все частицы рассматриваемого объема жидкости. Это силы тяжести и силы инерции (силы инерции проявляются в движущейся жидкости, поэтому их учитывает раздел гидродинамика) .
Массовые силы пропорциональны массе жидкости, а для однородной жидкости, плотность которой одинакова во всех точках, — объему. Поэтому массовые силы называют еще объемными.

К поверхностным относятся силы, действующие на поверхности жидкости. Это, например, атмосферное давление, действующее на жидкость в открытом сосуде, или силы трения, возникающие в движущейся жидкости между отдельными слоями и стенками сосуда (в покоящейся жидкости силы трения отсутствуют) .

Жидкость, находящаяся в состоянии покоя, может находиться только под действием силы тяжести и поверхностных сил, вызванных внешним давлением (например, атмосферным) . Внешние силы давления являются нормальными сжимающими поверхностными силами (считается, что жидкость не сопротивляется растяжению) . Все эти силы создают в неподвижной жидкости некоторую равнодействующую (результирующую) силу, которая называется гидростатической силой .

Покоящаяся жидкость под воздействием гидростатической силы находится в напряженном состоянии, характеризуемом гидростатическим давлением.

Выделим в покоящейся жидкости произвольный объем (см. рис. 1) . Мысленно разделим этот объем произвольной плоскостью П . Выделим на полученном сечении точку А и некоторую площадку ΔS вокруг этой точки.
Через поверхность П давление передается со стороны отсеченной части I на часть II . Сила ΔP , действующая на рассматриваемую площадку ΔS и есть гидростатическая сила.

Отношение гидростатической силы к площади поверхности (выделенного сечения) жидкости называют средним гидростатическим давлением. Истинное гидростатическое давление в данной точке жидкости может быть определено, как предел, к которому стремится среднее гидростатическое давление при бесконечном уменьшении рассматриваемой площадки ΔS :

p = lim ΔP/ΔS при ΔS стремящемся к нулю.

Гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует, и величина его в произвольной точке не зависит от ориентации этой площадки в пространстве.

Это утверждение вытекает из условий:
— неподвижности жидкости, поскольку при любом перемещении жидкости неизбежно возникают касательные напряжения;
— равновесия рассматриваемого элементарного (бесконечно малого) объема, поскольку равновесие может быть достигнуто лишь при равенстве всех действующих на рассматриваемый элементарный объем внешних сил (предполагается, что весом бесконечно малого объема жидкости можно пренебречь) .
При этом выделенный объем может иметь любую произвольную форму – куба, правильной пирамиды и т. д. – в любом случае легко доказать, что силы, действующие на грани этого объема будут одинаковы во всех направлениях.

Основное уравнение гидростатики. Закон Паскаля.

Выделим в однородной жидкости, находящейся в покое, элементарный объем ΔV в виде прямоугольного параллелепипеда с площадью горизонтального основания ΔS и высотой H (см. рис. 2) .
Рассмотри условия равновесия выделенного элементарного объема.

Пусть давление на плоскость верхнего основания равно р₁ , а на плоскость нижнего основания – р .
Силы давления действующие на вертикальные грани выделенного параллелепипеда взаимно уравновешиваются как равные по величине и противоположно направленные.
На горизонтальные грани действуют силы давления, направленные вертикально: на верхнюю грань эта сила будет равна р₁ΔS (направлена вниз) , на нижнюю – pΔS (направлена вверх) .

На верхнюю и нижнюю грани рассматриваемого параллелепипеда действуют силы, обусловленные давлением на жидкость со стороны внешней среды (например, атмосферного давления) и вес (сила тяжести) элементарного столбика жидкости над каждой из горизонтальных граней параллелепипеда.
Очевидно, что разность сил тяжести, действующих на верхнюю и нижнюю площадку, будет равна весу жидкости, заключенной в объеме рассматриваемого параллелепипеда, который равен ρgΔV ,
где ρ – плотность жидкости, g – ускорение свободного падения, ΔV – объем параллелепипеда: ΔV = HΔS .

Исходя из условия равновесия выделенного элементарного параллелепипеда объемом ΔV , можно утверждать, что сумма всех внешних сил, действующих на параллелепипед равна нулю, т. е.:

pΔS – p₁ΔS – ρgΔV = pΔS – p₁ΔS – ρgΔSH = 0 .

Преобразовав эту формулу, получим величину гидростатического давления на нижнюю горизонтальную площадку:

Если верхняя грань параллелепипеда граничит с внешней средой (например, атмосферой) , оказывающей давление р₀ на жидкость, то формула может быть переписана в виде:

Это выражение является основным уравнением гидростатики .

Итак, гидростатическое давление в любой точке внутри покоящейся жидкости равно сумме давления на свободную поверхность со стороны внешней среды и давления столба жидкости высотой, равной глубине погружения точки (т. е. ее расстоянию от свободной поверхности жидкости) .

На основании основного уравнения гидростатики может быть сформулирован закон Паскаля: внешнее давление, производимое на свободную поверхность покоящейся жидкости, передается одинаково всем ее точкам по всем направлениям.

Блез Паскаль (Blaise Pascal, 1623 — 1662) — выдающийся французский ученый — математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.

Любопытны цитаты из популярного сборника высказываний Паскаля, не потерявшие актуальность и в наши дни.
Вот некоторые из них:

• Искание истины совершается не с весельем, а с волнением и беспокойством; но все таки надо искать ее потому, что, не найдя истины и не полюбив ее, ты погибнешь.
• Прошлое и настоящее — наши средства, только будущее — наша цель.
• Нас утешает любой пустяк, потому что любой пустяк приводит нас в уныние.
• Когда человек пытается довести свои добродетели до крайних пределов, его начинают обступать пороки.
• Справедливость должна быть сильной, а сила должна быть справедливой.
• Истина так нежна, что чуть только отступил от нее, впадаешь в заблуждение, но и заблуждение это так тонко, что стоит только немного отклониться от него, и оказываешься в истине.
• Величие не в том, чтобы впадать в крайность, но в том, чтобы касаться одновременно двух крайностей и заполнять промежуток между ними.
• Изучая истину, можно иметь троякую цель: открыть истину, когда ищем ее; доказать ее, когда нашли; наконец, отличить от лжи, когда ее рассматриваем.
• Сила добродетели человека должна измеряться не его усилиями, а его повседневной жизнью.
• Лишь в конце работы мы обычно узнаём, с чего нужно было её начать.
• Существует достаточно света для тех, кто хочет видеть, и достаточно мрака для тех, кто не хочет.
• Человек — это приговорённый к смерти, казнь которого откладывается на время его жизни.

Умер Паскаль после тяжелой и продолжительной болезни в возрасте 39 лет, оставив после себя яркий след в науке.
Имя этого ученого увековечено в названиях одной из единиц международной системы СИ, языка программирования Paskal и лунного кратера.

Пример решения задачи с использованием закона Паскаля

Водолазы при подъеме затонувшего судна работали на глубине 50 м. Определить давление p воды на этой глубине и силу P давления на скафандр водолаза, если площадь его поверхности S равна 1 м 2 .
Атмосферное давление считать равным 1013 МПа (0,1013×106 Па), плотность воды – 1000 кг/м 3 .

Решение:

Определим давление, оказываемое столбом воды на глубине 50 м (в Па) :

ρgH = 1000×9,81×50 = 4,9×105 Па.

Применив основное уравнение гидростатики, с учетом атмосферного давления, найдем давление на глубине 50 м:

p = p₀ + ρgH = 1,013×105 + 4,9×105 = 5,91×105 Па ≈ 0,59 МПа.

Силу давления столба воды на скафандр водолаза определим по формуле:

P = pS = 5,91×105×1 = 591000 Н = 591 кН.

Основное уравнение гидростатики и закон Паскаля широко применяются при решении многих инженерных задач. Свойства жидкости передавать производимое на нее давление без изменения используется при конструировании гидравлических прессов, домкратов, гидроаккумуляторов, гидроприводов и других механизмов. Основной принцип работы этих устройств основа на пропорциональной разности сил, приложенных к поршням гидроцилиндров, имеющих разный диаметр: P₁S₂ = P₂S₁ .

Видео:Закон БернуллиСкачать

Гидравлика.

Видео:21. Энергия и ее видыСкачать

1. Методы применения законов гидравлики.

1. Аналитический. Цель применения этого метода – устанавливать зависимость между кинематическими и динамическими характеристиками жидкости. С этой целью пользуются уравнениями механики; в итоге получают уравнения движения и равновесия жидкости.

Для упрощенного применения уравнений механики пользуются модельными жидкостями: например, сплошная жидкость.

По определению, ни один параметр этого континуума (сплошной жидкости) не может быть прерывным, в том числе его производное, причем в каждой точке, если нет особых условий.

Такая гипотеза позволяет установить картину механического движения и равновесия жидкости в каждой точке континуума пространства. Еще одним приемом, применяемом для облегчения решения теоретических задач, является решение задачи для одномерного случая со следующим обобщением для трехмерного. Дело в том, что для таких случаев не так трудно установить среднее значение исследуемого параметра. После этого можно получить другие уравнения гидравлики, наиболее часто применяемые.

Однако этот метод, как и теоретическая гидромеханика, суть которой составляет строго математический подход, не всегда приводит к необходимому теоретическому механизму решения проблемы, хотя и неплохо раскрывает ее общую природу проблемы.

2. Экспериментальный. Основным приемом, по этому методу, является использование моделей, согласно теории подобий: при этом полученные данные применяются в практических условиях и становится возможным уточнение аналитических результатов.

Наилучшим вариантом является сочетание двух вышеназванных методов.

Современную гидравлику трудно себе представить без применения современных средств проектирования: это высокоскоростные локальные сети, автоматизированное рабочее место конструктора и прочее.

Поэтому современную гидравлику нередко называют вычислительной гидравликой.

Свойства жидкости.

Поскольку газ – следующее агрегатное состояние вещества, то у этих форм вещества существует свойство, общее для обоих агрегатных состояний. Это свойство текучести.

Исходя из свойств текучести, рассмотрев жидкое и газообразное агрегатное состояние вещества, увидим, что жидкость – то состояние вещества, в котором его уже невозможно сжимать (или можно сжать бесконечно мало). Газ – такое состояние того же вещества, в котором его можно сжать, то есть газ можно назвать сжимаемой жидкостью, точно так же, как и жидкость – несжимаемым газом.

Другими словами, особых принципиальных различий, кроме сжимаемости, между газом и жидкостью не наблюдается.

Несжимаемую жидкость, равновесие и движение которой изучает гидравлика, называют также капельной жидкостью.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

2. Основные свойства жидкости.

Плотность жидкости.

Если рассмотреть произвольный объем жидкости W, то он имеет массу М.

Если жидкость однородна, то есть если во всех направлениях ее свойства одинаковы, то плотность будет равна.

Где М – масса жидкости.

Если требуется узнать r в каждой точке А объема W, то.

Где D – элементарность рассматриваемых характеристик в точке А.

Сжимаемость.

Характеризуется коэффициентом объемного сжатия.

Из формулы видно, что речь идет о способности жидкостей уменьшать объем при единичном изменении давления: из-за уменьшения присутствует знак минус.

Температурное расширение.

Суть явления втом, что слой с меньшей скоростью «тормозит» соседний. В итоге появляется особое состояние жидкости, из-за межмолекулярных связей у соседних слоев. Такое состояние называют вязкостью.

Отношение динамической вязкости к плотности жидкости называется кинематической вязкостью.

Поверхностное натяжение: из-за этого свойства жидкость стремится занимать наименьший объем, например, капли в шарообразных формах.

В заключение приведем краткий список свойств жидкостей, которые рассмотрены выше.

4. Объемное сжатие.

6. Температурное расширение.

7. Сопротивление растяжению.

8. Свойство растворять газы.

9. Поверхностное натяжение.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

3. Силы, действующие в жидкости.

Жидкости делятся на покоящиеся и движущиеся.

Здесь же рассмотрим силы, которые действуют на жидкость и вне ее в общем случае.

Сами эти силы можно разделить на две группы.

1. Силы массовые. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой ΔМ = ρW действует сила ΔF, в зависимости от ее массы.

Пусть объем ΔW содержит в себе точку А. Тогда в точке А:

Где FА – плотность силы в элементарном объеме.

Плотность массовой силы – векторная величина, отнесена к единичному объему ΔW; ее можно проецировать по осям координат и получить: Fх, Fу, Fz. То есть плотность массовой силы ведет себя, как массовая сила.

Примерами этих сил можно назвать силы тяжести, инерции (кориолисова и переносная силы инерции), электромагнитные силы.

Однако в гидравлике, кроме особых случаев, электромагнитные силы не рассматривают.

2. Поверхностные силы. Таковыми называют силы, которые действуют на элементарную поверхность Δw, которая может находиться как на поверхности, так и внутри жидкости; на поверхности, произвольно проведенной внутри жидкости.

Таковыми считают силы: силы давления которые составляют нормаль к поверхности; силы трения которые являются касательными к поверхности.

Если по аналогии (1) определить плотность этих сил, то:

Нормальное напряжение в точке А:

Касательное напряжение в точке А:

И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

4. Гидростатическое давление и его свойства.

Общие дифференциальные уравнения равновесия жидкости – уравнения Л. Эйлера для гидростатики.

Если взять цилиндр с жидкостью (покоящейся) и провести через него линию раздела, то получим жидкость в цилиндре из двух частей. Если теперь приложить некоторое усилие к одной части, то оно будет передаваться другой через разделяющую плоскость сечения цилиндра: обозначим эту плоскость S = w.

Если саму силу обозначить как то взаимодействие, передаваемое от одной части к другой через сечение Δw, и есть гидростатическое давление.

Если оценить среднее значение этой силы,

Рассмотрев точку А как предельный случай w, определяем:

Если перейти к пределу, то Δw переходит в точку А.

Мы доказали, что во всех трех направлениях (их мы выбрали произвольно) скалярное значение сил одно и то же, то есть не зависит от ориентации сечения Δw.

Вот это скалярное значение приложенных сил и есть гидростатическое давление, о котором говорили выше: именно это значение, сумма всех составляющих, передается через Δw.

Другое дело, что в сумме (р_х + р_у + р_z) какая-то составляющая окажется равной нулю.

Как мы в дальнейшем убедимся, в определенных условиях гидростатическое давление все же может быть неодинаково в различных точках одной и той же покоящейся жидкости, т. е.

Свойства гидростатического давления.

1. Гидростатическое давление всегда направлено по нормали к поверхности и его величина не зависит от ориентации поверхности.

2. Внутри покоящейся жидкости в любой точке гидростатическое давление направлено по внутренней нормали к площадке, проходящей через эту точку.

3. Для любых двух точек одного и того же объема однородной несжимаемой жидкости (ρ = соnst).

Где ρ – плотность жидкости;

П₁, П₂ – значение поле массовых сил в этих точках.

Поверхность, для любых двух точек которой давление одно и то же, называется поверхностью равного давления.

Видео:Основной закон гидростатикиСкачать

5. Равновесие однородной несжимаемой жидкости под воздействием силы тяжести.

Это равновесие описывается уравнением, которое называется основным уравнением гидростатики.

Для единицы массы покоящейся жидкости.

Для любых двух точек одного и того же объема, то.

Полученные уравнения описывают распределение давления в жидкости, которая находится в равновесном состоянии. Из них уравнение (2) является основным уравнением гидростатики.

Для водоемов больших объемов или поверхности требуется уточнения: сонаправлен ли радиусу Земли в данной точке; насколько горизонтальна рассматриваемая поверхность.

Где ρgh – весовое давление, которое соответствует единичной высоте и единичной площади.

Давление р называют абсолютным давлением р_абс.

Если р > р_абс, то р – р_атм = р₀ + ρgh – р_атм – его называют избыточным давлением:

Видео:Основные понятия гидродинамики линия токаСкачать

6. Законы Паскаля. Приборы измерения давления.

Что произойдет в других точках жидкости, если приложим некоторое усилие Δр? Если выбрать две точки, и приложить к одной из них усилие Δр1, то по основному уравнению гидростатики, во второй точке давление изменится на Δр₂.

Откуда легко заключить, что при равности прочих слагаемых должно быть.

Мы получили выражение закона Паскаля, который гласит: изменение давления в любой точке жидкости в равновесном состоянии передается во все остальные точки без изменений.

До сих пор мы исходили из предположения, что ρ = соnst. Если иметь сообщающийся сосуд, который заполнен двумя жидкостями с ρ₁≠ ρ₂, причем внешнее давление р₀= р₁= р_атм, то согласно (1):

Где h₁, h₂ – высота от раздела поверхности до соответствующих свободных поверхностей.

Давление – физическая величина, которая характеризует силы, направленные по нормали к поверхности одного предмета со стороны другого.

Если силы распределены нормально и равномерно, то давление.

Где – F суммарная приложенная сила;

S – поверхность, к которой приложена сила.

Если силы распределены неравномерно, то говорят о среднем значении давления или считают его в отдельно взятой точке: например, в вязкой жидкости.

Приборы для измерения давления.

Одним из приборов, которым измеряют давление, является манометр.

Недостатком манометров является то, что у них нее большой диапазон измерений: 1—10 кПа.

По этой причине в трубах используют жидкости, которые «уменьшают» высоту, например, ртуть.

Следующим прибором для измерения давления является пьезометр.

Видео:Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

7. Анализ основного уравнения гидростатики.

Высоту напора принято называть пьезометрической высотой, или напором.

Согласно основному уравнению гидростатики,

Где ρ – плотность жидкости;

G – ускорение свободного падения.

Р2, как правило, задается р₂= р_атм, поэтому, зная h_А и h_Н, нетрудно определить искомую величину.

2. р₁= р₂= р_атм. Совершенно очевидно, что из ρ = соnst, g = соnst следует, что h_А= h_Н. Этот факт называют также законом сообщающихся сосудов.

Вакуум измеряется в тех же единицах, что и давление.

Пьезометрический напор.

Вернемся к основному гидростатическому уравнению. Здесь z – координата рассматриваемой точки, которая отсчитывается от плоскости ХОY. В гидравлике плоскость ХОY называется плоскостью сравнения.

Отсчитанную от этой плоскости координату z называют пооразному: геометрической высотой; высотой положения; геометрическим напором точки z.

В том же основном уравнении гидростатики величии на р/ρgh – также геометрическая высота, на которую поднимается жидкость в результате воздействия давления р. р/ρgh так же, как и геометрическая высота, измеряется в метрах. В случае, если через другой конец трубы на жидкость действует атмосферное давление то жидкость в трубе поднимается на высоту р_изб/ρgh, которую называют вакуумметрической высотой.

Высоту, соответствующую давлению рвак, называют вакуумметрической.

В основном уравнении гидростатики сумма z + р/ρgh – гидростатический напор Н, различают также пьезометрический напор Н_n , который соответствует атмосферному давлению р_атм/ρgh:

Видео:ОСНОВНЫЕ ЗАКОНЫ ГИДРОСТАТИКИСкачать

8. Гидравлический пресс.

Гидравлический пресс служит для совершения на коротком пути большей работы. Рассмотрим работу гидравлического пресса.

Для этого, чтобы совершалась работа над телом, надо воздействовать на поршень с некоторым давлением Р. Это давление, как и Р₂, создается следующим образом.

Когда поднимается поршень насоса с площадью нижней поверхности S₂, то он закрывает первый клапан и открывает второй. После заполнения цилиндра водой второй клапан закрывается, открывается первый.

В результате вода через трубу заполняет цилиндр и давит на поршень с помощью нижнего сечения S₁ с давлением Р₂.

Это давление, как давление Р₁, сжимает тело.

Совершенно очевидно, что Р₁– это то же самое давление, что и Р₂, разница только в том, что они воздействуют на разные по величине площади S₂ и S₁.

Другими словами, давления:

Выразив р = Р₂/S₂ и подставив в первую формулу, получим:

Из полученной формулы следует важный вывод: на поршень с большей площадью S₁ со стороны поршня с меньшей площадью S₂ передается давление во столько раз большее, во сколько раз S₁> S₂.

Однако на практике из-за сил трения до 15 % этой передаваемой энергии теряется: тратится на преодоление сопротивления сил трения.

И все же у гидравлических прессов коэффициент полезного действия η= 85 % – достаточно высокий показатель.

В гидравлике формула (2) перепишется в следующем виде:

Где Р₁ обозначено как R;

Гидравлический аккумулятор.

Гидравлический аккумулятор служит для поддержания давления в подключенной к нему системе постоянным.

Достижение постоянства давления происходит следующим образом: сверху на поршень, на его площадь ω, действует груз Р.

Труба служит для передачи этого давления по всей системе.

Если в системе (механизме, установке) жидкости в избытке, то избыток по трубе поступает в цилиндр, поршень поднимается.

При недостатке жидкости поршень опускается, и создаваемое при этом давление р, по закону Паскаля, передается на все части системы.

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

9. Определение силы давления покоящейся жидкости на плоские поверхности. Центр давления.

Для того, чтобы определить силу давления, будем рассматривать жидкость, которая находится в покое относительно Земли. Если выбрать в жидкости произвольную горизонтальную площадь ω, то, при условии, что на свободную поверхность действует р_атм= р₀, на ω оказывается избыточное давление:

Поскольку в (1) ρgh_ω есть не что иное, как mg, так как h_ω и ρV = m, избыточное давление равно весу жидкости, заключенной в объеме h_ω. Линия действия этой силы проходит по центру площади ω и направлена по нормали к горизонтальной поверхности.

Формула (1) не содержит ни одной величины, которая характеризовала бы форму сосуда. Следовательно, Р_изб не зависит от формы сосуда. Поэтому из формулы (1) следует чрезвычайно важный вывод, так называемый гидравлический парадокс – при разных формах сосудов, если на свободную поверхность оказывается одно и тоже р₀, то при равенстве плотностей ρ, площадей ω и высот h давление, оказываемое на горизонтальное дно, одно и то же.

При наклонности плоскости дна имеет место смачивание поверхности с площадью ω. Поэтому, в отличие от предыдущего случая, когда дно лежало в горизонтальной плоскости, нельзя сказать, что давление постоянно.

Чтобы определить его, разобьем площадь ω на элементарные площади dω, на любую из которых действует давление.

По определению силы давления,

Причем dР направлено по нормали к площадке ω.

Теперь, если определить суммарную силу которая воздействует на площадь ω, то ее величина:

Определив второе слагаемое в (3) найдем Р_абс.

Получили искомые выражения для определения давлений, действующих на горизонтальную и наклонную.

Рассмотрим еще одну точку С, которая принадлежит площади ω, точнее, точку центра тяжести смоченной площади ω. В этой точке действует сила Р₀= ρ₀ω.

Сила действует в любой другой точке, которая не совпадает с точкой С.

Видео:Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать

10. Определение силы давления в расчетах гидротехнических сооружений.

При расчетах в гидротехнике интерес представляет сила избыточного давления Р, при:

Где рО – давление, приложенное к центру тяжести.

Говоря о силе, будем иметь в виду силу, приложенную в центре давления, хотя будем подразумевать, что это – сила избыточного давления.

Для определения Р_абс воспользуемся теоремой моментов, из теоретической механики: момент равнодействующей относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси.

Теперь, согласно этой теореме о равнодействующем моменте:

Поскольку при р₀ = р_атм, Р = ρgh_{ц. е}.ω, поэтому dР = ρghd_ω = ρgsinθld_ω, следовательно (здесь и далее для удобства не будем различать р_изб и р_абс), с учетом Р и dР из (2), а также после преобразований следует:

Если теперь перенесем ось момента инерции, то есть линию уреза жидкости (ось О_Y) в центр тяжести ω, то есть в точку С, то относительно этой оси момент инерции центра давления точки D будет J₀.

Поэтому выражение для центра давления (точка D) без переноса оси момента инерции от той же линии уреза, совпадающие с осью О_Y, будет иметь вид:

Окончательная формула для определения места расположения центра давления от оси уреза жидкости:

Где S = ωl_ц.д. – статистический момент.

Окончательная формула для l_ц.д. позволяет определить центр давления при расчетах гидротехнических сооружений: для этого разбивают участок на составные участки, находят для каждого участка l_ц.д. относительно линии пересечения этого участка (можно пользоваться продолжением этой линии) со свободной поверхностью.

Центры давления каждого из участков находятся ниже центра тяжести смоченной площади по наклонной стенке, точнее по оси симметрии, на расстоянии I₀/ωl_ц.u.

Видео:Физика 10 класс (Урок№13 - Работа. Мощность. Энергия. Закон сохранения механической энергии.)Скачать

11. Общая методика определения сил на криволинейные поверхности.

1. В общем случае, это давление:

Где Wg – обьем рассматриваемой призмы.

В частном случае, направления линий действия силы на криволинейную поверхность тела, давления зависят от направляющих косинусов следующего вида:

Сила давления на цилиндрическую поверхность с горизонтальной образующей полностью определена. В рассматриваемом случае ось О_Y направлена параллельно горизонтальной образующей.

2. Теперь рассмотрим цилиндрическую поверхность с вертикальной образующей и направим ось О_Z параллельно этой образующей, что значит ω_z = 0.

Поэтому по аналогии, как и в предыдущем случае,

Где h’_ц.т. – глубина центра тяжести проекции под пьезометрическую плоскость;

H’ _ц.т. – то же самое, только для ω_у.

Аналогично, направление определяется направляющими косинусами.

Если рассмотреть цилиндрическую поверхность, точнее, объемный сектор, с радиусом γ и высотой h, с вертикальной образующей, то.

3. Осталось обобщить полученные формулы для прикладного применения произвольной криволинейной поверхности:

Видео:Гидравлика лекция 2Скачать

12. Закон Архимеда. Условия плавучести погруженных тел.

Следует выяснить условия равновесия погруженного в жидкость тела и следствия, вытекающие из этих условий.

Сила, действующая на погруженное тело – равнодействующая вертикальных составляющих Р_z1, Р_z2,т. е.:

Где Р_z1, Р_z2 – силы направленные вниз и вверх.

Это выражение характеризует силу, которую принято называть архимедовой силой.

Архимедовой силой является сила, равная весу погруженного тела (или его части): эта сила приложена в центр тяжести, направлена вверх и количественно равна весу жидкости, вытесненной погруженным телом или его частью. Мы сформулировали закон Архимеда.

Теперь разберемся с основными условиями плавучести тела.

1. Объем жидкости, вытесненной телом, называется объемным водоизмещением. Центр тяжести объемного водоизмещения совпадает с центром давления: именно в центре давления приложена равнодействующая сил.

2. Если тело погружено полностью, то объем тела W совпадает с W_Т, если нет, то W

Где ρ,ρ_Т – плотность жидкости и тела соответственно;

W– объемное водоизмещение;

W_Т – объем самого погруженного тела;

2) надводное, когда тело погружено частично; при этом глубину погружения низшей точки смоченной поверхности тела называют осадкой плавающего тела.

Ватерлинией называют линию пересечения погруженного тела по периметру со свободной поверхностью жидкости.

Площадью ватерлинии называется площадь погруженной части тела, ограниченной ватерлинией.

Линию, которая проходит через центры тяжести тела и давления, называют осью плавания, которая при равновесии тела вертикальна.

Видео:Якута А. А. - Механика - Эффект Доплера. Введение в гидро- и аэростатику. Закон АрхимедаСкачать

13. Метацентр и метацентрический радиус.

Способность тела восстанавливать свое первоначальное равновесное состояние после прекращения внешнего воздействия называют остойчивостью.

По характеру действия различают статистическую и динамическую остойчивость.

Поскольку мы находимся в рамках гидростатики, то и разберемся со статистической остойчивостью.

Если образовавшийся после внешнего воздействия крен необратим, то остойчивость неустойчива.

В случае сохранения после прекращения внешнего воздействия, равновесие восстанавливается, то остойчивость устойчива.

Условием статистической остойчивости является плавание.

Если плавание подводное, то центр тяжести должен быть расположен ниже центра водоизмещения на оси плавания. Тогда тело будет плавать. Если надводное, то остойчивость зависит от того, на какой угол θ повернулось тело вокруг продольной оси.

При θ о , после прекращения внешнего воздействия равновесие тела восстанавливается; если θ ≥ 15 о , то крен необратим.

Точку пересечения архимедовой силы с осью плавания называют метацентром: при этом проходит также через центр давления.

Метацентрическим радиусом называют радиус окружности, частью которой является дуга, по которой центр давления перемещается в метацентр.

Приняты обозначения: метацентр – М, метацентрический радиус – γ_м.

Где I₀ – центральный момент плоскости относительно продольной оси, заключенной в ватерлинии.

После введения понятия «метацентр» условия остойчивости несколько изменяются: выше говорили, что для устойчивой остойчивости центр тяжести должен находиться выше центра давления на оси плавания. Теперь предоложим, что центр тяжести не должен находиться выше метацентра. В противном случае силы и будут увеличивать крен.

Как очевидно, при крене расстояние δ между центром тяжести и центром давления меняется в пределах δ

При этом расстояние между центром тяжести и метацентром называют метацентрической высотой, которая при условии (2) положительна. Чем больше метацентрическая высота, тем меньше вероятность крена плавающего тела. Наличие остойчивости относительно продольной оси плоскости, содержащей в себе ватерлинию, является необходимым и достаточным условием остойчивости относительно поперечной оси той же плоскости.

Видео:Якута А. А. - Механика - Гидростатика. Уравнение Бернулли. Формула ПуайзеляСкачать

14. Методы определения движения жидкости.

Гидростатика изучает жидкость в ее равновесном состоянии.

Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение.

Гидродинамика также изучает движение жидкости, но в зависимости от воздействия приложенных к жидкости сил.

В кинематике используется сплошная модель жидкости: некоторый ее континуум. Согласно гипотезе сплошности, рассматриваемый континуум – это жидкая частица, в которой беспрерывно движется огромное количество молекул; в ней нет ни разрывов, ни пустот.

Если в предыдущих вопросах, изучая гидростатику, за модель для изучения жидкости в равновесии взяли сплошную среду, то здесь на примере той же модели будут изучать жидкость в движении, изучая движение ее частиц.

Для описания движения частицы, а через нее и жидкости, существуют два способа.

1. Метод Лагранжа. Этот метод не используется при описании волновых функций. Суть метода в следующем: требуется описать движение каждой частицы.

Начальному моменту времени t₀ соответствуют начальные координаты х₀, у₀, z₀.

Однако к моменту t они уже другие. Как видно, речь идет о движении каждой частицы. Это движение можно считать определенным, если возможно указать для каждой частицы координаты х, у, z в произвольной момент времени t как непрерывные функции от х₀, у₀, z₀.

Переменные х₀, у₀, z₀, t, называют переменными Лагранжа.

2. Метод определения движения частиц по Эйлеру. Движение жидкости в этом случае происходит в некоторой неподвижной области потока жидкости, в котором находятся частицы. В частицах произвольно выбираются точки. Момент времени t как параметр является заданным в каждом времени рассматриваемой области, которая имеет координаты х, у, z.

Рассматриваемая область, как уже известно, находится в пределах потока и неподвижна. Скорость частицы жидкости u в этой области в каждый момент времени t называется мгновенной местной скоростью.

Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается следующей системой:

Переменные в (2) х, у, z, t называют переменными Эйлера.

Видео:Вывод закона сохранения механической энергии | Физика 9 класс #22 | ИнфоурокСкачать

15. Основные понятия, используемые в кинематике жидкости.

Сутью вышеупомянутого поля скоростей являются векторные линии, которые часто называют линиями тока.

Линия тока – такая кривая линия, для любой точки которой в выбранный момент времени вектор местной скорости направлен по касательной (о нормальной составляющей скорости речь не идет, поскольку она равна нулю).

Формула (1) является дифференциальным уравнением линии тока в момент времени t. Следовательно, задав различные ti по полученным i, где i = 1,2, 3, …, можно построить линию тока: ею будет огибающая ломаной линии, состоящей из i.

Линии тока, как правило, не пересекаются в силу условия ≠ 0 или ≠ ∞. Но все же, если эти условия нарушаются, то линии тока пересекаются: точку пересечения называют особой (или критической).

1. Неустановившееся движение, которое так называется иззза того, что местные скорости в рассматриваемых точках выбранной области по времени изменяются. Такое движение полностью описывается системой уравнений.

2. Установившееся движение: поскольку при таком движении местные скорости не зависят от времени и постоянны:

Линии тока и траектории частиц совпадают, а дифференциальное уравнение для линии тока имеет вид:

Совокупность всех линий тока, которые проходят через каждую точку контура потока, образует поверхность, которую называют трубкой тока. Внутри этой трубки движется заключенная в ней жидкость, которую называют струйкой.

Струйка считается элементарной, если рассматриваемый контур бесконечно мал, и конечной, если контур имеет конечную площадку.

Сечение струйки, которое нормально в каждой своей точке к линиям тока, называется живым сечением струйки. В зависимости от конечности или бесконечной малости, площадь струйки принято обозначать, соответственно, ω и dω.

Некоторый объем жидкости, который проходит через живое сечение в единицу времени, называют расходом струйки Q.

16. Вихревое движение.

Особенности видов движения, рассматриваемых в гидродинамике.

Можно выделить следующие виды движения.

Неустановившееся, по поведению скорости, давления, температуры и т. д.; установившееся, по тем же параметрам; неравномерное, в зависимости от поведения тех же параметров в живом сечении с площадью; равномерное, по тем же признакам; напорное, когда движение происходит под давлением р > р_атм, (например, в трубопроводах); безнапорное, когда движение жидкости происходит только под действием силы тяжести.

Однако основными видами движения, несмотря на большое количество их разновидностей, являются вихревое и ламинарное движения.

Движение, при котором частицы жидкости вращаются вокруг мгновенных осей, проходящих через их полюсы, называют вихревым движением.

Это движение жидкой частицы характеризуется угловой скоростью, компонентами (составляющими), которой являются:

Вектор самой угловой скорости всегда перпендикулярен плоскости, в которой происходит вращение.

Если определить модуль угловой скорости, то.

Удвоив проекции на соответствующие координаты оси ω_х, ω_у, ω_z, получим компоненты вектора вихря.

Совокупность векторов вихря называется векторным полем.

По аналогии с полем скоростей и линией тока, существует и вихревая линия, которая характеризует векторное поле.

Это такая линия, у которой для каждой точки вектор угловой скорости сонаправлен с касательной к этой линии.

Линия описывается следующим дифференциальным уравнением:

В котором время t рассматривается как параметр.

Вихревые линии во многом ведут себя так же, как и линии тока.

Вихревое движение называют также турбулентным.

17. Ламинарное движение.

Это движение, называют также потенциальным (безвихревым) движением.

При таком движении отсутствует вращение частиц вокруг мгновенных осей, которые проходят через полюсы жидких частиц. По этой причине:

Выше отмечалось, что при движении жидкости происходит не только изменение положения частиц в пространстве, но и их деформация по линейным параметрам. Если рассмотренное выше вихревое движение является следствием изменения пространственного положения жидкой частицы, то ламинарное (потенциальное, или безвихревое) движение является следствием деформационных явлений линейных параметров, например, формы и объема.

Вихревое движение определялось направлением вихревого вектора.

Где υ – угловая скорость, которая является характеристикой угловых деформаций.

Деформацию этого движения характеризируют деформацией этих компонентов.

Но, поскольку при ламинарном движении υ_х=υ_у= υ_z= 0, то:

Из этой формулы видно: поскольку существуют частные производные, связанные между собой в формуле (4), то эти частные производные принадлежат некоторой функции.

18. Потенциал скорости и ускорение при ламинарном движении.

Функция φ называется потенциалом скорости.

С учетом этого, компоненты φ выглядят следующим образом:

Формулой (1) описывается неустановившееся движение, поскольку она содержит параметр t.

Ускорение при ламинарном движении.

Ускорение движения жидкой частицы имеет вид:

Где du/dt – полные производные по времени.

Ускорение можно представить в таком виде, исходя из.

Составляющие искомого ускорения.

Формула (4) содержит в себе информацию о полном ускорении.

Слагаемые υu_х/υt, υu_у/υt, υu_z/υt, называют местными ускорителями в рассматриваемой точке, которыми характеризуются законы изменения поля скоростей.

Если движение установившееся, то.

Само поле скоростей может быть названо конвекцией. Поэтому остальные части сумм, соответствующие каждой строке (4), называют конвективными ускорениями. Точнее, проекциями конвективного ускорения, которое характеризует неоднородность поля скоростей (или конвекций) в конкретный момент времени t.

Само полное ускорение можно назвать некоторой субстанцией, которая является суммой проекций.

19. Уравнение неразрывности жидкости.

Довольно часто при решении задач приходится определять неизвестные функции типа:

1) р = р (х, у, z, t) – давление;

2) n_х(х, у, z, t), nу(х, у, z, t), n_z(х, у, z, t) – проекции скорости на оси координат х, у, z;

3) ρ (х, у, z, t) – плотность жидкости.

Эти неизвестные, всего их пять, определяют по системе уравнений Эйлера.

Количество уравнений Эйлера всего три, а неизвестных, как видим, пять. Не хватает еще двух уравнений для того, чтобы определить эти неизвестные. Уравнение неразрывности является одним из двух недостающих уравнений. В качестве пятого уравнения используют уравнение состояния сплошной среды.

Формула (1) является уравнением неразрывности, то есть искомое уравнение для общего случая. В случае несжимаемости жидкости ∂ρ/dt = 0, поскольку ρ = соnst, поэтому из (1) следует:

Поскольку эти слагаемые, как известно из курса высшей математики, являются скоростью изменения длины единичного вектора по одному из направлений Х, Y, Z.

Что касается всей суммы в (2), то она выражает скорость относительного изменения объема dV.

Это объемное изменение называют пооразному: объемным расширением, дивергенцией, расхождением вектора скоростей.

Для струйки уравнение будет иметь вид:

Где Q – количество жидкости (расход);

ω– угловая скорость струйки;

∂l – длина элементарного участка рассматриваемой струйки.

Если давление установившееся или площадь живого сечения ω = соnst, то ∂ω /∂t = 0, т. е. согласно (3),

ρ∂Q/∂l = 0, следовательно,

20. Характеристики потока жидкости.

В гидравлике потоком считают такое движение массы, когда эта масса ограничена:

1) твердыми поверхностями;

2) поверхностями, которые разделяют разные жидкости;

3) свободными поверхностями.

В зависимости от того, какого рода поверхностями или их сочетаниями ограничена движущаяся жидкость, различают следующие виды потоков:

1) безнапорные, когда поток ограничен сочетанием твердой и свободной поверхностей, например, река, канал, труба с неполным сечением;

2) напорные, например, труба с полным сечением;

3) гидравлические струи, которые ограничены жидкой (как мы увидим позже, такие струйки называют затопленными) или газовой средой.

Живое сечение и гидравлический радиус потока. Уравнение неразрывности в гидравлической форме.

Сечение потока, с которого все линии тока нормальны (т. е. перпендикулярны), называется живым сечением.

Чрезвычайно важное значение имеет в гидравлике понятие о гидравлическом радиусе.

Для напорного потока с круглым живым сечением, диаметром d и радиусом r₀, гидравлический радиус выражается.

При выводе (2) учли.

Расход потока – это такое количество жидкости, которое проходит через живое сечение за единицу времени.

Для потока, состоящего из элементарных струек, расход:

Где dQ = dω – расход элементарного потока;

U– скорость жидкости в данном сечении.

21. Разновидность движения.

В зависимости от характера изменения поля скоростей различают следующие виды установившегося движения:

1) равномерное, когда основные характеристики потока – форма и площадь живого сечения, средняя скорость потока, в том числе по длине, глубине потока (если движение безнапорное), – постоянны, не изменяются; кроме того, по всей длине потока вдоль линии тока местные скорости одинаковы, а ускорений вовсе нет;

2) неравномерное, когда ни один из перечисленных для равномерного движения факторов не выполняется, в том числе и условие параллельности линий токов.

Существует плавно изменяющееся движение, которое все же считают неравномерным движением; при таком движении предполагают, что линии тока примерно параллельны, и все остальные изменения происходят плавно. Поэтому, когда направление движения и ось ОХ сонаправлены, то пренебрегают некоторыми величинами.

Uх ≈ U; Uу = Uz = 0. (1).

Уравнение неразрывности (1) для плавно изменяющегося движения имеет вид:

Аналогично для остальных направлений.

Поэтому такого рода движение называют равномерным прямолинейным;

3) если движение нестационарное или неустановившееся, когда местные скорости с течением времени изменяются, то в таком движении различают следующие разновидности: быстро изменяющееся движение, медленно изменяющееся движение, или, как часто его называют, квазистационарное.

Давление разделяют в зависимости от количества координат в описывающих его уравнениях, на: пространственное, когда движение трехмерное; плоское, когда движение двухмерное, т. е. Uх, Uу или Uz равна нулю; одномерное, когда движение зависит только от одной из координат.

В заключение отметим следующее уравнение неразрывности для струйки, при условии, что жидкость несжимаемая, т. е. ρ= соnst, для потока это уравнение имеет вид:

Где υ_iω_i – скорость и площадь одного и того же сечения с номером i.

Уравнение (3) называют уравнением неразрывности в гидравлической форме.

22. Дифференциальные уравнения движения невязкой жидкости.

Уравнение Эйлера служит одним из фундаментальных в гидравлике, наряду с уравнением Бернулли и некоторыми другими.

Изучение гидравлики как таковой практически начинается с уравнения Эйлера, которое служит исходным пунктом для выхода на другие выражения.

Попробуем вывести это уравнение. Пусть имеем бесконечно малый параллелепипед с гранями dхdуdz в невязкой жидкости с плотностью ρ. Он заполнен жидкостью и движется как составная часть потока. Какие силы действуют на выделенный объект? Это силы массы и силы поверхностных давлений, которые действуют на dV = dхdуdz со стороны жидкости, в которонаходится выделенный dV. Как силы массы пропорциональны массе, так и поверхностные силы пропорциональны площадям, на которые оказывается давление. Эти силы направлены к граням вовнутрь по нормали. Определим математическое выражение этих сил.

Назовем, как и при получении уравнения неразрывности, грани параллелепипеда:

1, 2 – перпендикулярные к оси О_Х и параллельные оси О_Y;

3, 4 – перпендикулярные к оси О_Y и параллельные оси О_Х;

5, 6 – перпендикулярные к оси О_Z и параллельные оси О_Х.

Теперь нужно определить, какая сила приложена к центру масс параллелепипеда.

Сила, приложенная к центру массы параллелепипеда, которая и заставляет эту жидкость совершать движение, есть сумма найденных сил, то есть.

Получили уравнение движения параллелепипеда с dV₁ по направлению оси Х.

Делим (1) на массу ρdхdуdz:

Полученная система уравнений (2) есть искомое уравнение движения невязкой жидкости – уравнение Эйлера.

К трем уравнениям (2) добавляются еще два уравнения, поскольку неизвестных пять, и решается система из пяти уравнений с пятью неизвестными: одним из двух дополнительных уравнений является уравнение неразрывности. Еще одним уравнением является уравнение состояния. Например, для несжимаемой жидкости уравнением состояния может быть условие ρ = соnst.

Уравнение состояния должно быть выбрано таким образом, чтобы оно содержало хотя бы одно из пяти неизвестных.

23. Уравнение Эйлера для разных состояний.

Уравнение Эйлера для разных состояний имеет разные формы записи. Поскольку само уравнение получено для общего случая, то рассмотрим несколько случаев:

1) движение неустановившееся.

2) жидкость в покое. Следовательно, Uх = Uу = Uz = 0.

В таком случае уравнение Эйлера превращается в уравнение равномерной жидкости. Это уравнение также дифференциальное и является системой из трех уравнений;

3) жидкость невязкая. Для такой жидкости уравнение движения имеет вид.

Где Fl – проекция плотности распределения сил массы на направление, по которому направлена касательная к линии тока;

DU/dt – ускорение частицы.

Подставив U = dl/dt в (2) и учтя, что (∂U/∂l)U = 1/2(∂U 2 /∂l), получим уравнение.

Мы привели три формы уравнения Эйлера для трех частных случаев. Но это не предел. Главное – правильно определить уравнение состояния, которое содержало хотя бы один неизвестный параметр.

Уравнение Эйлера в сочетании с уравнением неразрывности может быть применено для любого случая.

Уравнение состояния в общем виде:

Таким образом, для решения многих гидродинамических задач оказывается достаточно уравнения Эйлера, уравнения неразрывности и уравнения состояния.

С помощью пяти уравнений легко находятся пять неизвестных: р, Uх, Uу, Uz, ρ.

Невязкую жидкость можно описать и другим уравнением.

24. Форма Громеки уравнения движения невязкой жидкости.

Уравнения Громеки – попросту другая, несколько преобразованная форма записи уравнения Эйлера.

Например, для координаты х.

Чтобы его преобразовать, используют уравнения компонентов угловой скорости для вихревого движения.

Преобразовав точно так же у-вую и z-вую компоненту, окончательно приходим к форме Громеко уравнения Эйлера.

Уравнение Эйлера было получено российским ученым Л. Эйлером в 1755 г., и преобразовано в вид (2) опять же российским ученым И. С. Громекой в 1881 г.

Уравнение Громеко (под воздействием массовых сил на жидкость):

– dП = Fхdх + Fуdу + Fzdz, (4).

То для компонентов Fу, Fz можно вывести те же выражения, что и для Fх, и, подставив это в (2), прийти к (3).

25. Уравнение Бернулли.

Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ωх, ωу,ωz угловой скорости w.

Условием того, что движение является установившимся, является отсутствие ускорения, то есть условие равенства нулю частных производных от всех компонентов скорости:

Если теперь сложить.

Если проецировать перемещение на бесконечно малую величину dl на координатные оси, то получим:

Dх = Uхdt; dу = Uу dt; dz = Uzdt. (3).

Теперь помножим каждое уравнение (3) соответственно на dх, dу, dz, и сложим их:

Предположив, что правая часть равна нулю, а это возможно, если вторая или третья строки равны нулю, получим:

Нами получено уравнение Бернулли.

26. Анализ уравнения Бернулли.

Это уравнение есть не что иное, как уравнение линии тока при установившемся движении.

Отсюда следуют выводы:

1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.

2) пропорциональны строки 1 и 2, т. е.

Уравнение (2) является уравнением вихревой линии. Выводы из (2) аналогичны выводам из (1), только линии тока заменяют вихревые линии. Одним словом, в этом случае условие (2) выполняется для вихревых линий;

3) пропорциональны соответствующие члены строк 2 и 3, т. е.

Где а – некоторая постоянная величина; если подставить (3) в (2), то получим уравнение линий тока (1), поскольку из (3) следует:

Здесь следует интересный вывод о том, что векторы линейной скорости и угловой скорости сонаправлены, то есть параллельны.

В более широком понимании надо представить себе следующее: так как рассматриваемое движение установившееся, то получается, что частицы жидкости движутся по спирали и их траектории по спирали образуют линии тока. Следовательно, линии тока и траектории частиц – одно и то же. Движение такого рода называют винтовым.

4) вторая строка определителя (точнее, члены второй строки) равна нулю, т. е.

Но отсутствие угловой скорости равносильно отсутствию вихревости движения.

5) пусть строка 3 равна нулю, т. е.

Но это, как нам уже известно, условие равновесия жидкости.

Анализ уравнения Бернулли завершен.

27. Примеры прикладного применения уравнения Бернулли.

Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые силы действуют на рассматриваемую жидкость. Поэтому рассмотрим две ситуации.

Одна массовая сила.

В этом случае подразумевается сила тяжести, которая выступает в качестве единственной массовой силы. Очевидно, что в этом случае ось Z и плотность распределения Fz силы Ппротивонаправлены, следовательно,

Fх = Fу = 0; Fz = —g.

Поскольку – dП = Fхdх + Fуdу + Fzdz, то – dП = Fzdz,окончательно dП = —gdz.

Интегрируем полученное выражение:

Где С – некоторая постоянная.

Подставив (1) в уравнение Бернулли, имеем выражение для случая воздействия на жидкость только одной массовой силы:

Если разделить уравнение (2) на g (поскольку оно постоянное), то.

Мы получили одну из самых часто применяемых в решении гидравлических задач формул, поэтому следует ее запомнить особенно хорошо.

Если требуется определить расположение частицы в двух разных положениях, то выполняется соотношение для координат Z₁ и Z₂, характеризующие эти положения.

Можно переписать (4) в другой форме.

28. Случаи, когда массовых сил несколько.

В этом случае усложним задачу. Пусть на частицы жидкости действуют следующие силы: сила тяжести; центробежная сила инерции (переносит движение от центра); кориолисовая сила инерции, которая заставляет частицы вращаться вокруг оси Z с одновременным поступательным движением.

В этом случае мы получили возможность представить себе винтовое движение. Вращение происходит с угловой скоростью w. Нужно представить себе криволинейный участок некоторого потока жидкости, на этом участке поток как бы вращается вокруг некоторой оси с угловой скоростью.

Частным случаем такого потока можно считать гидравлическую струю. Вот и рассмотрим элементарную струйку жидкости и применим в отношении к ней уравнение Бернулли. Для этого поместим элементарную гидравлическую струю в координатную систему ХYZ таким образом, чтобы плоскость YОХ вращалась вокруг оси О_Z.

Будем считать, что U – местная скорость жидкости во вращающейся плоскости YОХ. Пусть.

Составляющие силы тяжести (то есть ее проекции на оси координат), отнесенные к единичной массе жидкости. К этой же массе приложена вторая сила – сила инерции ω 2 r, где r – расстояние от частицы до оси вращения ее компоненты.

Из-за того, что ось ОZ «не вращается».

Окончательно уравнение Бернулли. Для рассматриваемого случая:

Или, что одно и то же, после деления на g.

Если рассмотреть два сечения элементарной струйки, то, применив вышеуказанный механизм, легко убедиться, что.

29. Энергетический смысл уравнения Бернулли.

Пусть теперь имеем установившееся движение жидкости, которая невязкая, несжимаемая.

И пусть она находится под воздействием сил тяжести и давления, тогда уравнение Бернулли имеет вид:

Теперь требуется идентифицировать каждое из слагаемых. Потенциальная энергия положения Z – это высота элементарной струйки над горизонтальной плоскостью сравнения. Жидкость с массой М на высоте Z от плоскости сравнения имеет некоторую потенциальную энергию МgZ. Тогда.

Это та же потенциальная энергия, отнесенная к единичной массе. Поэтому Z называют удельной потенциальной энергией положения.

Движущаяся частица с массой Ми скоростью u имеет вес МG и кинематическую энергию U2/2g. Если соотнести кинематическую энергию с единичной массой, то.

Полученное выражение есть не что иное, как последнее, третье слагаемое в уравнении Бернулли. Следовательно, U 2 / 2 – это удельная кинетическая энергия струйки. Таким образом, общий энергетический смысл уравнения Бернулли таков: уравнение Бернулли представляет собой сумму, содержащую в себе полную удельную энергию сечения жидкости в потоке:

1) если полная энергия соотнесена с единичной массой, то она есть сумма gz + р/ρ + U 2 / 2;

2) если полная энергия соотнесена с единичным объемом, то ρgz + р + рU 2 / 2;

3) если полная энергия соотнесена единичному весу, то полная энергия есть сумма z + р/ρg + U 2 / 2g. Не следует забывать, что удельная энергия определяется относительно плоскости сравнения: эта плоскость выбирается произвольно и горизонтально. Для любой пары точек, произвольно выбранной из потока, в котором установившееся движение и который движется потенциальноовихрево, а жидкость невязко-несжимаемая, суммарная и удельная энергия одинаковы, то есть распределены по потоку равномерно.

30. Геометрический смысл уравнения Бернулли.

Основу теоретической части такой интерпретации составляет гидравлическое понятие напор, которое принято обозначать буквой Н, где.

Гидродинамический напор Н состоит из следующих разновидностей напоров, которые входят в формулу (198) как слагаемые:

1) пьезометрический напор, если в (198) р = р_изг, или гидростатический, если р ≠ р_изг;

2) U 2 /2g – скоростной напор.

Все слагаемые имеют линейную размерность, их можно считать высотами. Назовем эти высоты:

1) z – геометрическая высота, или высота по положению;

2) р/ρg – высота, соответствующая давлению р;

3) U 2 /2g – скоростная высота, соответствующая скорости.

Геометрическое место концов высоты Н соответствует некоторой горизонтальной линии, которую принято называть напорной линией или линией удельной энергии.

Точно так же (по аналогии) геометрические места концов пьезометрического напора принято называть пьезометрической линией. Напорная и пьезометрическая линии расположены друг от друга на расстоянии (высоте) р_атм/ρg, поскольку р = р_изг + рат, т. е.

Отметим, что горизонтальная плоскость, содержащая напорную линию и находящаяся над плоскостью сравнения, называется напорной плоскостью. Характеристику плоскости при разных движениях называют пьезометрическим уклоном J_п, который показывает, как изменяется на единице длины пьезометрический напор (или пьезометрическая линия):

Пьезометрический уклон считается положительным, если он по течению струйки (или потока) уменьшается, отсюда и знак минус в формуле (3) перед дифференциалом. Чтобы J_п остался положительным, должно выполняться условие.

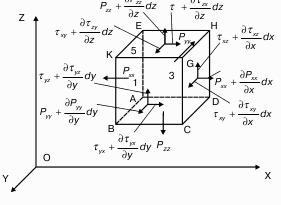
31. Уравнения движения вязкой жидкости.

Для получения уравнения движения вязкой жидкости рассмотрим такой же объем жидкости dV = dхdуdz, который принадлежит вязкой жидкости (рис. 1).

Грани этого объема обозначим как 1, 2, 3, 4, 5, 6.

Рис. 1. Силы, действующие на элементарный объем вязкой жидкости в потоке.

Будем считать, что для любой точки жидкости.

Тогда из шести касательных напряжений остается только три, поскольку попарно они равны. Поэтому для описания движения вязкой жидкости оказываются достаточными всего шесть независимых компонентов:

Аналогичное уравнение легко можно получить для осей О_Y и О_Z; объединив все три уравнения в систему, получим (предварительно разделив на ρ).

Полученную систему называют уравнением движения вязкой жидкости в напряжениях.

32. Деформация в движущейся вязкой жидкости.

В вязкой жидкости имеются силы трения, в силу этого при движении один слой тормозит другой. В итоге возникает сжатие, деформация жидкости. Из-за этого свойства жидкость и называют вязкой.

Если вспомнить из механики закон Гука, то по нему напряжение, которое возникает в твердом теле, пропорционально соответствующей относительной деформации. Для вязкой жидкости относительную деформацию заменяет скорость деформации. Речь идет об угловой скорости деформации частицы жидкости dΘ/dt, которую поодругому называют скоростью деформации сдвига. Еще Исааком Ньютоном установлена закономерность о пропорциональности силы внутреннего трения, площади соприкосновения слоев и относительной скорости слоев. Также им был установлен.

Коэффициент пропорциональности динамической вязкости жидкости.

Если выразить касательное напряжение через его компоненты, то.

А что касается нормальных напряжений (τ —это касательная составляющая деформации), которые зависимы от направления действия, то они зависят также от того, к какой площади они приложены. Это их свойство называют инвариантностью.

Сумма значений нормальных напряжений.

Чтобы окончательно установить зависимость между рudΘ/dt через зависимость между нормальными.

Где р′_хх– добавочные нормальные напряжения, которые и зависят от направления воздействия, по.

Аналогии с формулой (4) получим:

Сделав то же самое для компонентов р_уу, р_zz, получили систему.

33. Уравнение Бернулли для движения вязкой жидкости.

Элементарная струйка при установившемся движении вязкой жидкости.

Уравнение для этого случая имеет вид (приводим его без вывода, поскольку его вывод сопряжен с применением некоторых операций, приведение которых усложнило бы текст).

Потеря напора (или удельной энергии) h_Пр – результат того, что часть энергии превращается из механической в тепловую. Поскольку процесс необратим, то имеет место потеря напора.

Этот процесс называется диссипацией энергии.

Другими словами, h_Пр можно рассматривать как разность между удельной энергией двух сечений, при движении жидкости от одного к другому происходит потеря напора. Удельная энергия – это энергия, которую содержит единичная масса.

Поток с установившимся плавно изменяющемся движением. Коэффициент удельной кинематической энергии Х.

Для того, чтобы получить уравнение Бернулли в этом случае, приходится исходить из уравнения (1), то есть из струйки надо переходить в поток. Но для этого нужно определиться, что представляет собой энергия потока (которая состоит из суммы потенциальной и кинематической энергий) при плавно изменяющемся потоке.

Разберемся с потенциальной энергией: при плавном изменении движения, если поток установившийся.

Окончательно при рассматриваемом движении давление по живому сечению распределено согласно гидростатическому закону, т. е.

Где величину Х называют коэффициентом кинетической энергии, или коэффициентом Кориолиса.

Коэффициент Х всегда больше 1. Из (4) следует:

34. Гидродинамический удар. Гидро– и пьезо– уклоны.

В силу плавности движения жидкости для любой точки живого сечения потенциальная энергия Еп = Z + р/ρg. Удельная кинетическая Ек= Хυ 2 /2g. Поэтому для сечения 1–1 полная удельная энергия.

Сумму правой части (1) также называют гидродинамическим напором Н. В случае невязкой жидкости U 2 = хυ 2 . Теперь остается учесть потери напора h_пр жидкости при ее движении к сечению 2–2 (или 3–3).

Например, для сечения 2–2:

Следует отметить, что условие плавной изменяемости должно быть выполнено только в сечениях 1–1 и 2–2 (только в рассматриваемых): между этими сечениями условие плавной изменяемости необязательно.

В формуле (2) физический смысл всех величин приведен ранее.

В основном все так же, как и в случае с невязкой жидкостью, основная разница в том, что теперь напорная линия Е = Н= Z + р/ρg + Хυ 2 /2g не параллельна к горизонтальной плоскости сравнения, поскольку имеет места потери напора.

Степень потери напора hпр по длине называют гидравлическим уклоном J. Если потеря напора h_пр происходит равномерно, то.

Числитель в формуле (3) можно рассматривать как приращение напора dН на длине dl.

Поэтому в общем случае.

Знак минус перед dН/dl – потому, что изменение напора по его течению отрицательно.

Если рассмотреть изменение пьезометрического напора Z + р/ρg, то величину (4) называют пьезометрическим уклоном.

Напорная линия, она же линия удельной энергии, находится выше пьезометрической линии на высоту u 2 /2g: здесь то же самое, но только разница между этими линиями теперь равна хυ 2 /2g. Эта разница сохраняется также при безнапорном движении. Только в этом случае пьезометрическая линия совпадает со свободной поверхностью потока.

35. Уравнение Бернулли для неустановившегося движения вязкой жидкости.

Для того, чтобы получить уравнение Бернулли, придется определить его для элементарной струйки при неустановившемся движении вязкой жидкости, а затем распространять его на весь поток.

Прежде всего, вспомним основное отличие неустановившегося движения от установившегося. Если в первом случае в любой точке потока местные скорости изменяются по времени, то во втором случае таких изменений нет.

Приводим уравнение Бернулли для элементарной струйки без вывода:

Здесь учтено, что υω = Q; ρQ = m; mυ = (КД)_υ.

Так же, как и в случае с удельной кинетической энергией, считать (КД)_υ не таккто просто. Чтобы считать, нужно связать его с (КД)_υ. Для этого служит коэффициент количества движения.

Коэффициент а′ принято называть еще и коэффициентом Бусинеска. С учетом а′, средний инерционный напор по живому сечению.

Окончательно уравнение Бернулли для потока, получение которого и являлось задачей рассматриваемого вопроса имеет следующий вид:

Что касается (5), то оно получено из (4) с учетом того, что dQ = wdu; подставив dQ в (4) и сократив ω, приходим к (6).

Отличие hин от hпр прежде всего в том, что оно не является необратимым. Если движение жидкости с ускорением, что значит dυ/t > 0, то h_ин > 0. Если движение замедленное, то есть du/t

36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса.

Как нетрудно было убедиться в вышеприведенном опыте, если фиксировать две скорости в прямом и обратном переходах движения в режимы ламинарное → турбулентное, то.

Где υ₁ – скорость, при которой начинается переход из ламинарного в турбулентный режим;

υ₂ – то же самое при обратном переходе.

Где V – кинематическая вязкость жидкости;

D – диаметр трубы;

R– коэффициент пропорциональности.

В честь исследователя вопросов гидродинамики вообще и данного вопроса в частности, коэффициент, соответствующий uн. кр, называется критическим числом Рейнольдса Rе_кр.

Если изменить V и d, то Rе_кр не изменяется и остается постоянным.

Если Rе Rе_кр, то режим движения турбулентный из-за того, что υ> υ_кр.

37. Осредненные скорости. Пульсационные составляющие.

В теории турбулентного движения очень многое связано с именем исследователя этого движения Рейнольдса. Рассматривая хаотическое турбулентное движение, он представил мгновенные скорости, как некоторые суммы. Эти суммы имеют вид:

Где u_х, u_у, u_z – мгновенные значения проекций скорости;

Р, τ – то же самое, но для напряжений давления и трения;

Черта у величин наверху означает, что параметр усреднен по времени; у величин u′_х, u′_у, u′_z, р′, τ′ черта сверху означает, что имеется в виду пульсационная составляющая соответствующего параметра («добавка»).

Осреднение параметров по времени осуществляется по следующим формулам:

– интервал времени, в течение которого проводится осреднение.

Из формул (1) следует, что пульсируют не только проекции скорости, но и нормальные р ик асательные τ напряжения. Значения усредненных во времени «добавок» должны быть равны нулю: например для х-ой компоненты:

Интервал времени Т определяют достаточным, чтобы при повторном осреднении значение «добавки» (пульсирующей составляющей) не изменилось.

Турбулентное движение считается неустановившимся движением. Несмотря на возможное постоянство осредненных параметров, мгновенные параметры все же пульсируют. Следует запомнить: осредненная (по времени и в конкретной точке) и средняя (в конкретном живом сечении) скорости – не одно и то же:

Q – расход жидкости, которая течет со скоростью υ через w.

38. Средне квадратичное отклонение.

Принят стандарт, который называется среднеквадратическим отклонением. Для х.

Чтобы получить формулу для любого параметра «добавки» из формулы (1), достаточно заменить u_х в (1) на искомый параметр.

Среднеквадратичное отклонение можно относить к следующим скоростям: усредненная местная скорость данной точки; средняя по вертикали; средняя поживому сечению; максимальная скорость.

Обычно максимальная и средняя по вертикали скорости не используются; используются две из вышеперечисленных характерных скорости. Кроме них, используют также динамическую скорость.

Где R– гидравлический радиус;

J – гидравлический уклон.

Среднеквадратичное отклонение, отнесенное к средней скорости, есть, например, для х-ой компоненты:

Но лучшие результаты получаются, если среднеквадратичное отклонение относить к u_х, т. е. динамической скорости, например.

Определим степень (интенсивность) турбулентности, как называют величину е.

Однако лучшие результаты получаются, если за масштаб скорости (то есть за характерную скорость) взять динамическую скорость u_х.

Еще одним свойством турбулентности является частота пульсаций скорости. Средняя частота пульсации в точке с радиусом r от оси потока:

Где N – половина экстремума вне кривой мгновенных скоростей;

Т – период осреднения;

Т/N = 1/w– период пульсации.

39. Распределение скоростей при равномерном установившемся движении. Ламинарная пленка.

Все же, несмотря на вышеперечисленные и другие особенности, о которых не сказано из-за их невостребованности, основным признаком турбулентного движения является перемешивание частиц жидкости.

Принято об этом перемешивании с точки зрения количества говорить как о перемешивании молей жидкости.

Как мы убедились выше, с ростом числа Rе интенсивность турбулентности не растет. Несмотря на это, все же, например, у внутренней поверхности трубы (или у любой другой твердой стенки) существует некоторый слой, в пределах которого все скорости, в том числе пульсационные «добавки», равны нулю: это очень интересное явление.

Этот слой принято называть вязким подслоем потока.

Само собой на границе соприкосновения с основной массой потока этот вязкий подслой все же имеет некоторую скорость. Следовательно, все изменения в основном потоке передаются и в подвязкий слой, но их значение очень мало. Это позволяет считать движение слоя ламинарным.

Ранее, считая, что эти передачи в подвязкий слой отсутствуют, слой назвали ламинарной пленкой. Теперь нетрудно убедиться, что с точки зрения современной гидравлики ламинарность движения в этом слое относительная (интенсивность ε в подвязком слое (ламинарной пленке) может достигать значения 0,3. Для ламинарного движения это достаточно большая величина).

Подвязкий слой ε_в очень тонкий по сравнению с основным потоком. Именно наличие этого слоя порождает потери напора (удельной энергии).

Что касается толщины ламинарной пленки δ_в, то она обратно пропорциональна числу Rе. Это более наглядно видно из следующего сравнения толщины в зонах потока при турбулентном движении.

Вязкий (ламинарный) слой – 0

40. Распределение скоростей в «живом» сечении потока.

Современной гидродинамике удалось разрешить эти проблемы, применив метод статистического анализа. Основным орудием этого метода является то, что исследователь выходит за рамки традиционных подходов и применяет для анализа некие средние по времени характеристики потока.

Ясно, что в любой точке живого сечения любую мгновенную скорость и можно разложить на u_х, u_у, u_z компоненты.

Мгновенная скорость определяется по формуле:

Полученную скорость можно назвать скоростью, усредненной по времени, или средней местной эта скорость u_х – фиктивно постоянная и позволяет судить о характеристике потока.

Вычислив u_у,u_х можно получить вектор усредненной скорости.

Касательные напряжения τ = τ + τ ,

Определим и суммарное значение касательного напряжения τ. Поскольку это напряжение возникает из-за наличия сил внутреннего трения, то жидкость считают ньютоновой.

Если предположить, что площадь соприкосновения – единичная, то сила сопротивления.

Где μ – динамическая вязкость жидкости;

Dυ/dу – изменение скорости. Эту величину часто называют градиентом скорости, или скоростью сдвига.

В настоящее время руководствуются выражением, полученным в вышеупомянутом уравнении Прандтля:

Где ρ– плотность жидкости;

L– длина пути, на котором рассматривается движение.

Без вывода приводим окончательную формулу для пульсационной «добавки» касательного напряжения:

42. Параметры потока, от которых зависит потеря напора. Метод размерностей.

Неизвестный вид зависимости определяется по методу размерностей. Для этого существует π-теорема: если некоторая физическая закономерность выражена уравнением, содержащим к размерных величин, причем оно содержит п величин с независимой размерностью, то это уравнение может быть преобразовано в уравнение, содержащее (к-п) независимых, но уже безразмерных комплексов.

Для чего определимся: от чего зависят потери напора при установившемся движении в поле сил тяжести.

1. Геометрические размеры потока:

1) характерные размеры живого сечения l₁l₂;

2) длина рассматриваемого участка l;

3) углы, которыми завершается живое сечение;

4) свойства шероховатости: Δ– высота выступа и lΔ – характер продольного размера выступа шероховатости.

2. Физические свойства:

2) μ – динамическая вязкость жидкости;

3) δ – сила поверхностного натяжения;

4) Е_ж – модуль упругости.

3. Степень интенсивности турбулентности, характеристикой которой является среднеквадратичное значение пульсационных составляющих δu.

Теперь применим π-теорему.

Исходя из приведенных выше параметров, у нас набирается 10 различных величин:

Кроме этих, имеем еще три независимых параметра: l₁, ρ, υ. Добавим еще ускорение падения g.

Всего имеем к = 14 размерных величин, три из которых независимы.

Требуется получить (ккп) безразмерных комплексов, или, как их называют π-членов.

Для этого любой параметр из 11, который не входил бы в состав независимых параметров (в данном случае l₁, ρ, υ), обозначим как N_i, теперь можно определить безразмерный комплекс, который является характеристикой этого параметра N_i, то есть i-тый π-член:

Здесь углы размерности базовых величин:

Общий вид зависимости для всех 14 параметров имеет вид:

43. Равномерное движение и коэффициент сопротивления по длине. Формула Шези. Средняя скорость и расход потока.

При ламинарном движении (если оно равномерное) ни живое сечение, ни средняя скорость, ни эпюра скоростей по длине не меняются со временем.

При равномерном движении пьезометрический уклон.

Где l₁– длина потока;

H_l– потери напора на длине L;

R₀d – соответственно радиус и диаметр трубы.

В формуле (2) безразмерный коэффициент λ называют коэффициентом гидравлического трения или коэффициентом Дарси.

Если в (2) d заменить на гидравлический радиус, то следует.

Тогда с учетом того, что.

Эту формулу называют формулой Шези.

Называется коэффициентом Шези.

Если коэффициент Дарси λ – величина безразмерр.

Ная, то коэффициент Шези с имеет размерность.

Определимся с расходом потока с участием коэфф.

Преобразуем формулу Шези в следующий вид:

Называют динамической скоростью.

44. Гидравлическое подобие.

Понятие о подобии. Гидродинамическое моделирование.

Для исследования вопросов сооружения гидроэлектростанций применяют метод гидравлических подобий, суть которого состоит в том, что в лабораторных условиях моделируются точно такие же условия, что и в натуре. Это явление называют физическим моделированием.

Например, чтобы два потока были подобными, требуется их:

1) геометрическое подобие, когда.

Где индексы н, м соответственно означают «натура» и «модель».

Что значит, относительная шероховатость в модели такая же, как и в натуре;

2) кинематическое подобие, когда траектории соответствующих частиц, соответствующие линии тока подобны. Кроме того, если соответствующие части прошли подобные расстояния l_н, l_м, то отношение соответствующих времен движения выглядит следующим образом.

Где М_i – масштаб времени.

Такое же сходство имеется для скорости (масштаб скорости).

И ускорения (масштаб ускорения).

3) динамическое подобие, когда требуется, чтобы соответствующие силы были подобными, например, масштаб сил.

Таким образом, если потоки жидкости механически подобны, то они подобны гидравлически; коэффициенты М_l, М_t, М_υ, М_р и прочие называются масштабными множителями.

45. Критерии гидродинамического подобия.

Условия гидродинамического подобия требуют равенства всех сил, но это практически не удается.

По этой причине, подобие устанавливают по какой-нибудь из этих сил, которая в данном случае преобладает. Кроме того, требуется выполнение условий однозначности, которые включают в себя пограничные условия потока, основные физические характеристики и начальные условия.

Рассмотрим частный случай.

Преобладает влияние сил тяжести, например, при течении через отверстия или водосливы.

Если перейти к взаимоотношению Р_н и Р_м и выразить его в масштабных множителях, то.

После необходимого преобразования, следует.

Если теперь совершить переход от масштабных множителей к самим отношениям, то с учетом того, что l – характерный размер живого сечения, то.

В (4) комплекс υ 2 /gl называется критерием Фруди, который формулируется так: потоки, в которых преобладают силы тяжести, геометрически подобны, если.

Это второе условие гидродинамического подобия.

Нами получены три критерия гидродинамического подобия.

1. Критерий Ньютона (общие критерии).

2. Критерий Фруда.

3. Критерий Дарси.

Отметим только: в частных случаях гидродинамическое подобие может быть установлено также по.

Где Δ– абсолютная шероховатость;

R– гидравлический радиус;

J– гидравлический уклон.

46. Распределение касательных напряжений при равномерном движении.

При равномерном движении потеря напора на длине l_hе определяется:

Где χ – смоченный периметр,

W – площадь живого сечения,

L_hе – длина пути потока,

ρ, g – плотность жидкости и ускорение силы тяжести,

τ₀ – касательное напряжение вблизи внутренних стенок трубы.

Откуда с учетом.

Исходя из полученных результатов для τ₀, распределения касательного напряжения τ в произвольно выбранной точке выделенного объема, например, в точке r₀– r = t это расстояние равно:

Тем самым вводим касательное напряжение t на поверхности цилиндра, действующее на точку в r₀– r= t.

Из сравнений (4) и (3) следует:

Подставив r= r₀– t в (5), получим.

1) при равномерном движении распределение касательного напряжения по радиусу трубы подчиняется линейному закону;

2) на стенке трубы касательное напряжение максимально (когда r₀= r, т. е. t = 0), на оси трубы оно равно нулю (когда r₀= t).

R– гидравлический радиус трубы, получим, что.

47. Турбулентный равномерный режим движения потока.

Если рассмотреть плоское движение (т. е. потенциальное движение, когда траектории всех частиц параллельны одной и той же плоскости и являются функции ей двух координат и если движение неустановившееся), одновременно являющееся равномерным турбулентным в системе координат ХYZ, когда линии тока параллельны оси ОХ, то.

Усредненная скорость при сильно турбулентном движении.

Это выражение: логарифмический закон распределения скоростей для турбулентного движения.

При напорном движении поток состоит в основном из пяти областей:

1) ламинарная: приосевая область, где местная скорость максимальна, в этой области λ_лам= f(Rе), где число Рейнольдса Rе δ_в, труба считается «гидравлически шероховатой».

Характерно, что если для λ_лам = f(Rе –1 ), то в этом случае λ_гд = f(Rе – 0,25 );

4) эта область находится на пути перехода потока к подвязкому слою: в этой области λ_лам = (Rе, Δ/r0). Как видно, коэффициент Дарси уже начинает зависеть от абсолютной шероховатости Δ;

5) эта область называется квадратичной областью (коэффициент Дарси не зависит от числа Рейнольдса, но определяется почти полностью касательным напряжением) и является пристенной.

Эту область называют автомодельной, т. е. не зависящей от Rе.

В общем случае, как известно, коэффициент Шези.

Где п – коэффициент шероховатости;

R– гидравлический радиус.

48. Неравномерное движение: формула Вейсбаха и ее применение.

При равномерном движении потери напора, как правило, выражаются формулой.

Где потери напора h_пр зависят от скорости потока; она постоянна, поскольку, движение равномерное.

Следовательно, и формула (1) имеет соответствующие формы.

Действительно, если в первом случае.

То во втором случае.

Как видно, формулы (2) и (3) различаются только коэффициентом сопротивления х.

Формула (3) называется формулой Вейсбаха. В обоих формулах, как и в (1), коэффициент сопротивления – величина безразмерная, и в практических целях определяется, как правило, по таблицам.

Для проведения опыта по определению хм последовательность действий следующая:

1) должен быть обеспечен ход равномерности потока в исследуемом конструктивном элементе. Необходимо обеспечить достаточное удаление от входа пьезометров.

2) для установившегося движения вязкой несжимаемой жидкости между двумя сечениями (в нашем случае, это вход с х₁υ₁ и выход с х₂υ₂), применяем уравнение Бернулли:

В рассматриваемых сечениях поток должен быть плавно изменяющимся. Между сечениями могло бы произойти что угодно.

Поскольку суммарные потери напора.

То находим потери напора на этом же участке;

3) по формуле (5) находим, что h_м= h_пр– h_l, после этого по формуле (2) находим искомый коэффициент.

49. Местные сопротивления.

Что происходит после того, как поток вошел с некоторым напором и скоростью в трубопровод.

Это зависит от вида движения: если поток ламинарный, то есть его движение описывается линейным законом, тогда его кривая – парабола. Потери напора при таком движении достигают (0,2 × 0,4) × (υ 2 / 2g).

При турбулентном движении, когда оно описывается логарифмической функцией, потери напора – (0,1 × 1,5) × (υ 2 /2g).

После таких потерь напора движение потока стабилизируется, то есть восстанавливается ламинарный или турбулентный поток, каким и был входной.

Участок, на котором происходят вышеуказанные потери напора, восстанавливается по характеру, прежнее движение называется начальным участком.

А чему равна длина начального участка l_нач.

Турбулентный поток восстанавливается в 5 раз быстрее, чем ламинарный, при одних и тех же гидравлических сопутствующих данных.

Рассмотрим частный случай, когда поток не сужается, как рассмотрели выше, но внезапно расширяется. Почему происходят потери напора при такой геометрии потока?

Для общего случая:

Чтобы определить коэффициенты местного сопротивления, преобразуем (1) в следующий вид: разделив и умножив на υ₁ 2

Определим υ₂/υ₁ из уравнения неразрывности.

Остается заключить, что.

50. Расчет трубопроводов.

Задачи расчета трубопроводов.

Требуются решать следующие задачи:

1) требуется определить расход потока Q, при этом заданы напор Н; длина трубы l; шероховатость трубы Δ; плотность жидкости r; вязкость жидкости V (кинематическая);

2) требуется определить напор Н. Заданы расход потока Q; параметры трубопровода: длина l; диаметр d; шероховатость Δ; параметры жидкости: ρ плотность; вязкость V;

3) требуется определить необходимый диаметр трубопровода d. Заданы расход потока Q; напор Н; длина трубы l; ее шероховатость Δ; плотность жидкости ρ; ее вязкость V.

Методика решений задач одна и та же: совместное применение уравнений Бернулли и неразрывности.

Напор определяется выражением:

Поскольку J = Н / l.

Важной характеристикой трубопровода является величина, которая объединяет некоторые параметры трубопровода, исходя из диаметра трубы (рассматриваем простые трубы, где диаметр по всей длине l постоянен). Этот параметр к называют расходной характеристикой:

Если начинать наблюдение с самого начала трубопровода, то увидим: некоторая часть жидкости, не изменяясь, доходит до конца трубопровода транзитом.

Пусть это количество будет Q_т (транзитный расход).

Жидкость по пути частично раздается потребителям: обозначим эту часть как Q_р (путевой расход).

С учетом этих обозначений, в начале трубопровода.

Соответственно, в конце расход потока.

Что касается напора в трубопроводе, то:

51. Гидравлический удар.

Наиболее распространенным, то есть часто встречающимся видом неустановившегося движения является гидравлический удар. Это типичное явление при быстром или постепенном закрытии затворов (резкое изменение скоростей в некотором сечении потока приводит к гидравлическому удару). Как следствие, возникают давления, которые распространяются по всему трубопроводу волной.

Эта волна может быть разрушительной, если не принять специальные меры: могут разорваться трубы, выйти из строя насосные станции, возникнуть насыщенные пары со всеми разрушительными последствиями и т. д.

Гидравлический удар может порождать разрывы жидкости в трубопроводе – это не менее серьезная авария, чем разрыв трубы.

Наиболее часто встречающиеся причины гидравлического удара следующие: внезапное закрытие (открытие) затворов, внезапная остановка насосов при заполнении трубопроводов водой, выпуск воздуха через гидранты в оросительной сети, пуск насоса при открытом затворе.

Если это уже случилось, то как протекает гидравлический удар, какие последствия вызывает?

Все это зависит от того, по какой причине возник гидравлический удар. Рассмотрим основную из этих причин. Механизмы возникновения и протекания по остальным причинам сходны.

Мгновенное закрытие затвора.

Гидравлический удар, который происходит в этом случае – чрезвычайно интересное явление.

Пусть имеем открытый резервуар, от которого отводится гидравлическая прямолинейная труба; на некотором расстоянии от резервуара труба имеет затвор. Что произойдет при его мгновенном закрытии?

1) резервуар настолько велик, что процессы, происходящие в трубопроводе, в жидкости (в резервуаре) не отражаются;

2) потери напора до закрытия затвора ничтожны, следовательно, пьезометрическая и горизонтальная линии совпадают.

3) давление жидкости в трубопроводе происходит только с одной координатой, две другие проекции местных скоростей равны нулю; движение определяется только продольной координатой.

Воовторых, теперь внезапно закроем затвор – в момент времени t₀; могут произойти два случая:

1) если стенки трубопровода абсолютно неупругие, т. е. Е = ∞, и жидкость несжимаема (Е_ж = ∞), то движение жидкости также внезапно останавливается, что приводит к резкому росту давления у затвора, последствия могут быть разрушительны.

Приращение давления при гидравлическом ударе по формуле Жуковского:

52. Скорость распространения волны гидравлического удара.

В гидравлических расчетах немалый интерес представляет скорость распространения ударной волны гидравлического удара, как и сам гидравлический удар. Как ее определить? Для этого рассмотрим круглое поперечное сечение в упругом трубопроводе. Если рассмотреть участок длиной Δl, то выше этого участка за время Δt жидкость еще движется со скоростью υ₀, кстати, как и до закрытия затвора.

Поэтому в соответствующей длине l объем ΔV ′ войдет жидкость Q = ω₀υ₀, т. е.

Где площадь круглого поперечного сечения – объем, образовавшийся в результате повышения давления и, как следствие этого, из-за растяжек стены трубопровода ΔV₁. Объем, который возник из-за роста давления на Δр обозначим как ΔV₂. Значит, тот объем, который возник после гидравлического удара, есть.

ΔV ′ входит в ΔV.

Определимся теперь: чему будут равны ΔV₁ и ΔV₂.

В результате растяжки трубы произойдет приращение радиуса трубы на Δr, то есть радиус станет равным r= r₀+ Δr. Из-за этого увеличится круглое сечение поперечного сечения на Δω = ω– ω₀. Все это приведет к приращению объема на.

Следует иметь в виду, что индекс ноль означает принадлежность параметра к начальному состоянию.

Что касается жидкости, то ее объем уменьшится на ΔV₂ из-за приращения давления на Δр.

Искомая формула скорости распространения волны гидравлического удара.

Где ρ– плотность жидкости;

D/l – параметр, характеризующий толщину стенки трубы.

Очевидно, что чем больше D/l, тем меньше скорость распространения волны С. Если труба жесткая абсолютно, то есть Е = ∞, то, как следует из (4).

53. Дифференциальные уравнения неустановившегося движения.

Для того, чтобы составить уравнение любого вида движения, нужно проецировать все действующие силы на систему и приравнивать их сумму к нулю. Так и поступим.

Пусть имеем напорный трубопровод круглого сечения, в котором есть неустановившееся движение жидкости.

Ось потока совпадает с осью l. Если выделить на этой оси элемент dl, то, согласно вышеуказанному правилу, можно составить уравнение движения.

В приведенном уравнении проекции четырех сил, действующих на поток, точнее, на Δl, равны нулю:

1) ΔМ – силы инерции, действующие на элемент dl;

2) Δр – силы гидродинамического давления;

3) ΔТ – касательные силы;

4) ΔG – силы тяжести: здесь мы, говоря о силах, имели в виду проекции сил, действующих на элемент Δl.

Перейдем к формуле (1), непосредственно к проекциям действующих сил на элемент Δt, на ось движения.

1. Проекции поверхностных сил:

1) для гидродинамических сил Δр проекцией будет.

2) для касательных сил ΔТ.

Проекция касательных сил имеет вид:

2. Проекция сил тяжести Δ ΔG на элемент Δ Δ

3. Проекция сил инерции Δ ΔМ равна.

54. Истечение жидкости при постоянном напоре через малое отверстие.

Будем рассматривать истечение, которое происходит через малое незатопленное отверстие. Для того, чтобы отверстие считать малым, должны выполняться условия:

1) напор в центре тяжести Н >> d, где d – высота отверстия;

2) напор в любой точке отверстия практически равен напору в центре тяжести Н.

Что касается затопленности, то таковой считают истечение под уровень жидкости при условии, если не изменяются со временем: положение свободных поверхностей до и после отверстий, давление на свободные поверхности до и после отверстий, атмосферное давление по обе стороны от отверстий.

Таким образом, имеем резервуар с жидкостью, у которой плотность ρ, из которого через малое отверстие происходит истечение под уровень. Напор Н в центре тяжести отверстия постоянен, что значит, скорости истечения постоянны. Следовательно, движение установившееся. Условием равенства скоростей на противоположных вертикальных границах отверстий является условие d ≤ 0,1Н, где d – наибольший вертикальный размер.

Ясно, что нашей задачей является определение скорости истечения и расхода жидкости в нем.

Сечение струи, отстоящее от внутренней стенки резервуара на расстояние 0,5d, называют сжатым сечением струи, которое характеризуется коэффициентом сжатия.

Формулы определения скорости и расхода потока:

Где υ₀ называется коэффициентом скорости.

Теперь выполним вторую задачу, определим расход Q. По определению.

Обозначим Еυ₀= μ₀, где μ₀ – коэффициент расхода, тогда.

Различают следующие разновидности сжатия:

1. Полное сжатие – это такое сжатие, которое происходит по всему периметру отверстия, в противном случае сжатие считается неполным сжатием.

2. Совершенное сжатие является одной из двух разновидностей полного сжатия. Это такое сжатие, когда кривизны траектории, следовательно, и степень сжатия струи наибольшие.

Подводя итог, заметим, что неполная и несовершенная формы сжатий приводят к росту коэффициента сжатия. Характерной особенностью совершенного сжатияявляется то, что в зависимости от того, под воздействием каких сил происходит истечение.

55. Истечение через большое отверстие.

Отверстие считают малым, когда его вертикальные размеры d 0,1Н.

Рассматривая истечение через малое отверстие, практически пренебрегли различием скоростей в разных точках сечения струи. В этом случае поступить так же мы не сможем.

Задача та же: определить расход и скорости в сжатом сечении.

Поэтому расход определяют следующим способом: выделяют бесконечно малую горизонтальную высоту dz. Таким образом, получается горизонтальная полоса с переменной длиной bz. Тогда, интегрировав по длине, можно найти элементарный расход.

Где Z – переменный напор по высоте отверстия, на такую глубину погружен верх выбранной полосы;

μ – коэффициент расхода через отверстие;

B_z – переменная длина (или ширина) полосы.

Расход Q (1) можем определить, если μ = соnst и известна формула b_z= f(z). В общем случае, расход определяют по формуле.

Если форма отверстия прямоугольная, то bz= b = соnst, интегрировав (2), получаем:

Где Н₁, Н₂ – напоры на уровнях соответственно у верхней и у нижней кромок отверстия;

Нц – напор над центром отверстия;

D – высота прямоугольника.

Формула (3) имеет более упрощенный вид:

В случае истечения через круглое отверстие пределами интегрирования в (2) служат Н₁= Н_ц – r; Н₂ = Н_ц + r; Z = Н_ц – rсоsυ; d_z = ρsinυdυ; b_z = 2rυsinυ.

Избегая математического излишества, приведем конечную формулу:

Как видно из сравнений формул, особой разницы в формулах для расхода нет, только при больших и малых отверстиях коэффициенты расхода разные.

56. Коэффициент расхода системы.

Требуется выяснить вопрос о расходе, если истечение происходит по трубам, соединенным в одну систему, но имеющих разные геометрические данные. Здесь нужно рассмотреть каждый случай отдельно. Приведем некоторые из них.

1. Истечение происходит между двумя резервуарами при постоянном напоре через систему труб, у которых разные диаметры и длина. В этом случае на выходе системы Е= 1, следовательно, численно μ= υ, где Е, μ, υ – коэффициенты соответственно сжатия, расхода и скорости.

2. Истечение происходит через систему труб с разными ω(площадь поперечного сечения): при этом определяют суммарный коэффициент сопротивления системы, который состоит из таких же коэффициентов, но для каждого участка отдельно.

Истечение происходит в атмосферу через незатопленное отверстие. В этом случае.

Где Н = z = соnst – напор; μ, ω– коэффициент расхода и площадь сечения.

Для того, чтобы рассчитать расход, нужно в (1) вместо коэффициента расхода m подставить коэффициент расхода системы.

Поскольку в (2) коэффициент Кориолиса (или кинетической энергии) х отнесен к выходному сечению, где, как правило х ≈ 1.

Такое же истечение происходит через затопленное отверстие.

В этом случае расход определяется по формуле (3), где μ = μ_сист, ω– площадь выходного сечения. При отсутствии или незначительности скорости в приемнике или трубе коэффициент расхода заменяется на.

Нужно только иметь в виду, что при затопленном отверстии ζ вых = 1, и этот ζвых входит в ζсист.