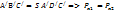Основное уравнение гидростатики его геометрический и энергетический смысл (4 видео)

Содержание

Диф-ые уравнения равновесия жидкости.
Основное уравнение гидростатики и его интерпретации
Основное уравнение гидростатики и его интерпретации
Основы гидравлики
Основные физические свойства жидкости.
Гидростатика
Основное уравнение гидростатики
Вакуум. Закон Паскаля.
🎦 Видео

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Диф-ые уравнения равновесия жидкости.

Дифференциальные уравнения равновесия покоящейся жидкости иначе называют дифференциальными уравнениями Эйлера. Они получены для общего случая относительного покоя жидкости. Возможны следующие варианты относительного покоя.

Первый вариант соответствует абсолютному покою или равномерному движению сосуда с жидкостью. Такой вариант рассматривался при выводе основного уравнения гидростатики.

Второй вариант – вращение сосуда с жидкостью с постоянной угловой скоростью Й вокруг центральной оси. Несмотря на то, что вся масса жидкости вращается вместе с сосудом, частицы жидкости друг относительно друга не перемещаются, следовательно, весь объём жидкости, как и в первом случае, представляет собой как бы твёрдое тело. Давление в каждой точке жидкости не меняется во времени и зависит только от координат. По этим причинам жидкость подпадает под определение покоящейся.

Третий вариант аналогичен второму, только вращение осуществляется вокруг произвольно расположенной вертикальной оси. Во втором и третьем случае свободная поверхность жидкости принимает новую форму, соответствующую новому равновесному положению жидкости.

В четвёртом варианте сосуд с жидкостью движется прямолинейно и равноускоренно. Такой случай проявляется, например, в процессе разгона или остановки автоцистерны с жидкостью. В этом случае жидкость занимает новое равновесное положение, свободная поверхность приобретает наклонное положение, которое сохраняется до изменения ускорения. Частицы жидкости друг относительно друга находятся в покое, и давление зависит только от координат.

11. Основное уравнение гидростатики.Основным законом (уравнением) гидростатики называется уравнение [1] :

— гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,

— плотность жидкости,

— ускорение свободного падения,

— высота точки над плоскостью сравнения (геометрический напор [2] ),

— гидростатический напор [3] .Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.Иногда основным законом гидростатики называют принцип Паскаля [4] .
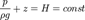
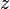
12-13. Геометрический и энергетический смысл основного уравнения гидростатики.
Геометрический смысл уравнения 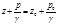(4):
— величина z фиксирует положение точки по отношению к плоскости хОу, называемой плоскостью сравнения.
— ординату z называют высотой положения, или геометрической высотой.
При р = р₀ имеем z = z₀.
Очевидно, что величина р/у имеет линейную размерность.
Она представляет собой высоту, на которую жидкость может подняться под влиянием давления. Эту высоту можно измерить. если поместить в жидкость вертикальную закрытую сверху трубку, из которой полностью выкачан воздух.
Высоту р/у называют высотой давлен и я, или приведенной высотой.
Она представляет собой высоту столба жидкости, вес которого при давлении, равном нулю на его свободной поверхности, уравновешивает давление в данной точке жидкости.
Чтобы пояснить энергетический смысл членов уравнения (4), введем понятие удельной энергии. Энергию, отнесенную к единице веса жидкости, называют удельной энергией.
Размерность удельной энергии равна размерности энергии (работы), деленной на размерность силы.Единица удельной энергии [Е] — м. Часть удельной потенциальной энергии частицы жидкости, зависящая только от ее положения относительно условной горизонтальной плоскости, количественно равной z, называется удельной энергией положения частицы.
Часть удельной потенциальной энергии частицы жидкости, зависящую только от ее давления, количественно равную р/у, называют удельной энергией давления частицы
Сумма 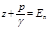представляет собой удельную потенциальную энергию частицы.
Наряду с этими понятиями в гидравлике широко используется понятие напора.
Так, величину z называют геометрическ и м напором в данной точке жидкости, а сумму z+р/γ=Н — гидростатическим напором.
Перепишем уравнение (3) в виде
p — p₀ = γ (z₀ — z) = γh откуда
p = p₀ + γh , (5)
где h — глубина погружения частицы жидкости под ее поверхность.
Это уравнение, так же как и (4), называют основным уравнением гидростатики. Разница между ними только в системе отсчета вертикальных расстояний (z и h).
Форма уравнения (4) удобна при изучении движения жидкости, так как сумма z + р/γ входит в уравнение движения жидкости.
Форма уравнения (5) удобна в расчетах давления на поверхности и в методике измерения давления в жидкости.
Величина р является абсолютным, или полным, давлением, р₀ — внешним (начальным) давлением. Произведение γh — вес столба жидкости высотой h с площадью основания, равной единице.
Поэтому γh можно назвать весовым давлением.Единицей давления, входящего в формулу (5), является паскаль (Па).
14. Закон Паскаля. Закон Паскаля формулируется так:Давление,производимое на покоящуюся жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям.Гидростатическое давление жидкости зависит от плотности р жидкости, от ускорения g свободного падения и от глубины h, на которой находится рассматриваемая точка. Оно не зависит от формы столба жидкости. Глубина h отсчитывается по вертикали от рассматриваемой точки до уровня свободной поверхности жидкости.В условиях невесомости гидростатическое давление в жидкости отсутствует, так как в этих условиях жидкость становится невесомой. Внешнее давление характеризует сжатие жидкости под действием внешней силы. Оно равно: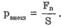
15.Избытачное и вакууметрическое давление.
Вакууметрическое давление: если абсолютное давление в точке атмосферного, то это превышение называется избыточным (нанометрическим) давлением.
16.Поверхность равного давления. Выделим в ж-ти, к. нах-ся в равновесии, бесконечно малый объем в виде параллелепипеда с ребрами dx,dy,dz. Складывая сумму проекций сил давления, массовых сил(X- проекция массовой силы на ось)на рассматриваемую ось, получим: pdydz-(p+d1pdx/d1x)dydz+ ρdxdydzX=0 После упрощения: (-d1p/ ρd1x)+X=0 Аналогично:(-d1p/ ρd1y)+Y=0, (-d1p/ ρd1z)+Z=0 Почленно умножив 1е ур-е на ρdx, 2е на ρdy, 3е на ρdz, получим основное ур-е гидростатики: dp= ρ(Xdx+Ydy+Zdz)[1]. В общем виде это ур-е интегрируется так: p=ρП+С, где П- некоторая потенциальная ф-я. В частных случаях в зависимости от конкретных Z,X,Y находим значение П,С и p. Из [1] можно получить ур-е для пов-ти равного давления. При p=const, ρ=const, dp=0 и тогда Xdx+Ydy+Zdz=0
17.Сила давления жидкости на плоские поверхности.Угол=90 градусов, ж-ть давит на пов-ть с площ. ω во всех точках, но давление неравномерное (в верхних 2 /₃ глубины воды от свободной поверхности.
Сила Р_впроходит через центр тяжести треугольника АВС, который находят с помощью криволинейных медиан. Равнодействующая Р пройдёт через точку пересечения направления действия сил Р_г и Р_впод углом β к горизонтальной поверхности, где:tg β = Р_в / Р_г21. Толщина стенки цилиндрической трубы, находящейся под избыточным давления.
Рассмотрим вопрос о нахождении допускаемого давления жидкости в трубе круглого сечения.
Мысленно разделив трубу на две части вертикальной (диаметральной) плоскостью, запишем, как определяется сила избыточного давления жидкости на одну половину трубы длиной L:

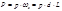
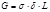
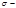
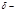
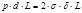
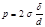
Эта сила уравновешивается двумя силами, приложенными к стенкам трубы в местах условного разреза, каждая из которых находится как: ,где растягивающее напряжение в стенках трубы; толщина стенки трубы. Таким образом,

Если напряжение в стенках трубы будет равно предельно- допускаемому, то допускаемое давление в трубе:
Для заданного избыточного давления в трубопроводе и материале трубы, можно найти толщину стенки трубы: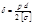
22. Плавучесть и остойчивость плавающих тел.
S
Если бы это равенство не соблюдалось, то тело бы начало двигаться.
Верт. Силы давления BAD и BCD- силы тяжести тел давления опираются на эти поверхности.
Результирующая сила:
Т.о на погруженное в жидкости тело действует вертикальная сила(вверх),равная силе тяжести жидкости в объем тела(з-н Архимеда)
Если G>P-тело тонет и наоборот.
При всплытии объем вытесненный телом воды меняется от W до W1. Всплытие прекратится, когда P=G.
Водоизмещение-сила тяжести жидкости в объеме воды погруженной в нее части тела.
Ватерлиния-линия ∩свободной поверхности жидк с боковой поверхностью плавающего тела.
При плавании тело может отклоняться по сторонам. Остойчивость-способность тела восстанавливать первоначальное положение.
Условия остойчивости: Лиия действия силы Р ∩ ось плавания в точке М, называется метацентром.
-расстояние от точки М до центра водоизмещения D (метацентрический радиус)
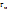
P и G обр пару сил. Если метацентр ниже центра тяжести →тело опрокидывается(неостойчивое плавание)
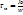
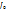
Метацентрический радиус: , где — момент инерции плоскости плавания относительно оси О-О1, W- водоизмещение.
23. Понятие об установившемся и неустановившемся движении жидкости. Неустановившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения т.е.:

и .

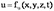
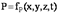
Примером неустановившегося движения может являться вытекание жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде постепенно меняется (уменьшается) по мере вытекания жидкости.
Установившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. u и P зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения:

и ,

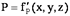
и, следовательно, , , , .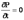
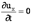
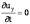
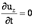
24.Линия тока и элементарная струйка.
Геометрические представления о движении жидкости можно получить с помощью выкторных линий, назыв линиями тока.
Линия тока-линия в каждой точке которой в данный момент времени соответ-ет определ система линий тока, вид расположение которых характеризует поле скоростей.
В турбулентном режиме линии тока имеют расхождения. При установившемся движении значения и направления скоростей не изменяются во времени и линии тока совпадают с траекториями движения частиц жидкости.Линии тока не могут пересекаться. Они дают фотографический снимок с картин распр-я в жидкости векторов.
Поверхность, образ-я линиями тока, проведенными через все точки какой-либо заданной линии наз поверхностью тока.
Часть движ-ия жидкости,огр поверхностью тока, подведенной в данное мгновение черз все точки бескнонечно малого замкнутого контура,наход-я в обл,занятой жидкостью, наз элеметарной струйкой.
через боковую поверхность элементарной струйки жидкость не перетекает. В каждой точке поверхности скорости напр-ия по нормалям и в пределах этой бесконечно малой поверхности принимает одинаковые значения.
Живые сечения струйки(элементарной) –ее нормальное(поперечное) сечение.
Площадь живого сечения может изменятся по длине струйки.
25.Поток жидкости, расход и средняя скорость потока.
Ввиду 2 /2g.
Связь между скоростью ии высотой h_ииспользована для конструирования приборов, позволяющих измерять скорости течения жидкости, а также и воздуха, или же скорости движения тела в воде или воздухе.
Такие приборы называют гидрометрическими, или напорными, трубками.
Простейшая гидрометрическая трубка 1 (см. рис. 3.5) неудобна в работе, так как отсчет h_и приходится делать в непосредственной близости от воды. Этот недостаток устраняется, если соединить в один прибор трубки напорную (динамическую) 2 и пьезометрическую (статическую) 4.
Плоскость нижнего среза статической трубки параллельна направлению скорости.
Если понизить давление в обеих трубках отсосом воздуха через трубку 3, оба уровня поднимутся, но h_ипри этом не. изменится.
Зная h_и, легко подсчитать скорость: 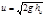Различают два основных типа гидрометрических трубок:
— трубка Пито — напорная трубка Г — образной формы, открытый конец которой, имеющий обтекаемую форму, воспринимает полное давление.

Видео:Основное уравнение гидростатики (задачи)Скачать

Основное уравнение гидростатики и его интерпретации

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Основное уравнение гидростатики и его интерпретации

Основное уравнение гидростатики и его интерпретации. Деление обеих сторон уравнения (3.26)на ru дает основное гидростатическое уравнение. |Р = справляется(3.36） Или, учитывая (2.5）、 +Р-concomE(3.37） Рассмотрим физический смысл 2-х членов с размерностью линейной массы, которая входит в основное гидростатическое уравнение. В емкости любой формы находится жидкость с плотностью p. давление на свободной поверхности жидкости равно p0 (рис.3.8). 31.

Представьте себе, что вертикальная труба трубочки P0, а не трубочка, через которую происходит полное разбавление (так называемая пустота Торричелли), подводится к точке A, которая находится внутри неподвижной жидкости на глубине H. далее, ДиПо Р точки а горизонтальная линия жидкости поднимается вдоль этой трубки на определенную высоту H над точкой А, называемую высотой давления. Если предположить, что точка А принадлежит судну, то из зависимости (3.30): Р = Ро + РФ-(3.38).

Всякое внешнее давление, действующее на свободную поверхность жидкости, находящейся в равновесии, передается внутрь во все точки жидкости без изменения. Людмила Фирмаль

Та же точка давления, но принадлежит трубе П0. П = По + ппы-(3-39） От внешнего давления П0), p’O = 0 на поверхности жидкости в трубке образуется полный вакуум, высота давления которого равна (3.39） * «=Гг Строго говоря, пространство над жидкой горизонтальной линией П0 должно быть заполнено жидким паром. Однако в нормальном температурном диапазоне, предполагая, что давление на свободной поверхности жидкости в трубке равно нулю, давление насыщенного пара значительно ниже атмосферного, чем можно пренебречь.

Жидкость в состоянии покоя обладает определенным запасом потенциальной энергии, то есть способностью выполнять работу. Предполагая, что базовый объем жидкости массы cU сосредоточен в точке A, можно проделать некоторую работу. Во-первых, он падает с высоты r на плоскость xOy. Таким образом, для выбранной опорной плоскости существует определенный потенциальный запас энергии yeg = КУИ; (3.41） Во-вторых, путем поднятия давления p на высоту H * * накапливается потенциальная энергия, способная выполнить эту задачу ёЕр=ааНА. (3.42） потенциальная энергия жидкого основного объема.

Таким образом, для данного объема жидкости гидростатический напор относительно выбранной плоскости сравнения — величина постоянная. Людмила Фирмаль

В гидравлике принято иметь дело с так называемой удельной энергией Е, то есть энергией относительно единицы веса жидкости, находящейся в точке А. Затем удельная потенциальная энергия в точке выпуска =(3-45） Итак, с энергетической точки зрения сумма величин, входящих в основное гидростатическое уравнение (3.36) + 2-это конкретный P＆ То есть она относится к единице веса, то есть потенциальной энергии жидкости в точке issue. In это дело〜Часть удельной потенциальной энергии это удельная энергия давления, часть удельной потенциальной энергии это удельная энергия положения.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Основы гидравлики

Учебные вопросы:

Видео:Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Основные физические свойства жидкости.

В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.

Жидкости подразделяют на два вида:

Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами).

К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие

Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию.К газообразным жидкостям относятся все газы.

К основным физическим свойствам жидкости относятся:

Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.

Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.

Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях

Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.

В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.

Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.

Гидростатика

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Гидростатическое давление обладает свойствами

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.8 ) и на ее свободную поверхность действует давление P0 . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем:

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Пьезометрический и гидростатический напоры

Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине присоединены пьезометры I и II (рис. 9).

Давление на свободной поверхности в сосуде больше атмосферного. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю.

Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой. За плоскость сравнения может быть принят уровень земли, пола.

Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота.

Пьезометрическая высота – мера манометрического давления в точке А. Приведенная высота – мера абсолютного давления в точке В. Разность высот , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.

Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:

Подставив это выражение в формулу (1) получим:

это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором Hs.

В уравнении (5) Hs=const для любой точки жидкости, а не зависит от положения точки. Значит:

Поэтому, сколько бы мы пьезометров не подключили, во всех пьезометрах жидкость установится на одном уровне: плоскость, соответствующая уровню П–П, называется пьезометрической плоскостью, а уровню Н–Н – напорной плоскостью.

Пьезометрический напор является мерой удельной потенциальной энергии жидкости. Предположим, что вес частицы жидкости в точке А. равен G. о отношении к плоскости сравнения О – О запас потенциальной энергии положения равен G*z, где -Z высота от плоскости О – О до точки А.

Под действием избыточного гидростатического давления Pm частица, находящаяся на глубине h , может подняться на высоту hp, то есть она обладает потенциальной энергией давления равной G*hp. Полная потенциальная энергия частицы жидкости весом G равна G*z+G*hp.

Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:

Аналогично, гидростатический напор Hs является также мерой удельной потенциальной энергии жидкости, но большей по сравнению Hp на величину удельной потенциальной энергии атмосферного давления.

Вакуум. Закон Паскаля.

Вакуум — пространство, свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, содержащую газ при давлении значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного падения молекул газа λ и характерным размером среды d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий, средний и высокий вакуум.

Насос для демонстрации вакуума

Законом Паскаля в гидростатике называется следующее утверждение,сформулированное французским учёным Блезом Паскалем: давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические процессы и др.

В законе Паскаля речь идет не о давлениях в разных точках гидравлической системы, а о возмущениях давления в разных точках, поэтому закон справедлив и для жидкости в поле силы тяжести.

В случае движущейся несжимаемой жидкости можно условно говорить о справедливости закона Паскаля, ибо добавление произвольной постоянной величины к давлению не меняет вида уравнения движения жидкости, однако в этом случае термин закон Паскаля обычно не применяется. Для сжимаемых жидкостей (газов) закон Паскаля, вообще говоря, несправедлив.

Виды движения жидкости

Виды движения жидкости бывают:

Неустановившимся – называют движение жидкости, все или некоторые характеристики которого изменяются во времени, т. е. давление и скорость зависят как от координат , так и от времени

Примерами неустановившегося движения являются опорожнение резервуаров, водохранилищ, движение воды в реках при переменном уровне (при паводках, сбросах воды через плотину) и т. д.

сброс воды через плотину

Установившимся – наз. движение жидкости неизменное во времени, при котором давление и скорость являются функциями только координат, но не зависит от времени. u = f1(x, y, z); p = f2(x, y, z).

Установившееся движение подразделяется на:

Равномерное движение характеризуется постоянством параметров по длине потока. Примерами такого движения являются движения в трубах постоянного сечения и в каналах правильной формы. Поле линий тока равномерного движения – семейство параллельных прямых.

При неравномерном движении скорость, глубина, площади сечений потока изменяются по его длине. Из неравномерных движений можно выделить так называемое плавно изменяющееся движение, которое характеризуется малой кривизной линий тока и малым углом расхождения линий тока .

В зависимости от причин, вызывающих движение, и условий, в которых оно происходит, различают:

напорное движение
безнапорное движение

Напорное движение происходит в потоке, со всех сторон ограниченном твердыми стенками. Давление во всех точках потока отлично от атмосферного и может быть как больше, так и меньше последнего. Движение происходит под действием разности давлений по длине потока, которая может быть создана водонапорной башней, питающим баком, насосной установкой.

Безнапорное движение происходит под действием силы тяжести при наличии свободной поверхности жидкости. Примерами безнапорного движения является движение в реках, каналах и трубах, когда сечение последних не полностью заполнено жидкостью.

Гидродинамика

Предметом изучения гидродинамики является движущаяся жидкость. Как было указано ранее, все без исключения физические и химические процессы, которые составляют основу промышленных технологических процессов, происходят в динамических условиях, в условиях движения текучих сред.

При движении жидкостей под воздействием внешних сил в потоках прежде всего формируются поля скоростей микро- и макрочастиц, которые определяют формирование температурных и полей концентраций веществ, что в конечном итоге обусловливает скорость протекания процессов.

На движущуюся жидкость, кроме сил, которые действовали на покоящуюся жидкость (поверхностные силы гидростатического давления и массовые силы: силы тяжести и внешние силы инерции), действуют дополнительные силы инерции и силы трения. В отличие от гидростатического давления, величина которого не зависит от ориентации поверхности, на которое оно действует, возникающее при движении гидродинамическое давление благодаря развитию напряжениям сдвига (касательным силам), различно в направлении осей X, Y и Z.

Наличие сил внутреннего трения между движущимися частицами жидкости (в соответствии с законом внутреннего трения Ньютона) является первопричиной различия скоростей движения в различных точках по поперечному сечению канала. Характер этого различия, который обусловливается характером связи между давлением и скоростью движения частиц в любой точке потока. Это и является основной задачей теории гидродинамики.

Уравнение неразрывности потока.

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 15 расходы во входном и выходном сечениях напорной трубы равны: q1 = q2.

Схема к уравнению неразрывности потока.

С учётом, что q = Vw, получим уравнение неразрывности потока:

Если отсюда выразим скорость для выходного сечения:

то легко заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

Ламинарный и турбулентный режим движения жидкости.

Наблюдения показывают, что в природе существует два разных движения жидкости:

слоистое упорядоченное течение – ламинарное движение, при котором слои жидкости скользят друг друга, не смешиваясь между собой;
турбулентное неурегулированное течение, при котором частицы жидкости движутся по сложным траекториям, и при этом происходит перемешивание жидкости.

От чего зависит характер движения жидкости, установил Рейнольдс в 1883 году путем. Эксперименты показали, что переход от ламинарного к турбулентному движению происходит при определенной скорости (критическая скорость), которая для труб различных диаметров неодинакова: при увеличении диаметра она увеличивается, критическая скорость так же увеличивается при увеличении вязкости жидкости. Рейнольдс вывел общие условия существования ламинарного и турбулентных режимов движения жидкости. По Рейнольдсу режима движения жидкости зависят от безразмерного числа, которое учитывает основные, определяющие это движение: среднюю скорость, диаметр трубы, плотность жидкости и ее абсолютную вязкость.

Это число называется числом Рейнольдса:

Число Рейнольдса, при котором происходит переход от одного режима движения жидкости в другой режим, называется критическим .

При числе Рейнольдса наблюдается ламинарный режим движения, при числе Рейнольдса – турбулентный режим движения жидкости. Чаще критическое значение числа принимают равным это значение соответствует переходу движения жидкости от турбулентного режима к ламинарного.

При переходе от ламинарного режима движения жидкости к турбулентному критическое значение имеет большее значение. Критическое значение числа Рейнольдса увеличивается в трубах, сужаются, и уменьшается в тех, что расширяются. Это объясняется тем, что при сужении поперечного сечения скорость движения частиц увеличивается, поэтому тенденция к поперечного перемещения уменьшается.

Уравнение Бернулли.

Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

p — плотность жидкости,

v— скорость потока,

h— высота, на которой находится рассматриваемый элемент жидкости,

p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

g— ускорение свободного падения.

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии .

Соотношение, близкое к приведенному выше, было получено в 1739 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Bernoulli Johann 1667-1748

СВОЙСТВА ГАЗОВ И ЖИДКОСТЕЙ

Список литературы:

1. В.П. Гусев «Основы гидравлики», Томск, 2009 г.

2. Бретшнайдер С. «Свойства газов и жидкостей», Москва