3.1. В жидкости действуют только распределенные силы потому, что:
а) жидкость обладает вязкостью; б) жидкость обладает текучестью; в) жидкость обладает способностью изменять свой объем при изменении давления и температуры.
Ответ: б).
3.2. Распределенные силы, действующие в жидкости, называются:
а) коэффициентами сил; б) напряжениями; в) усилиями.
Ответ: б).
3.3. Напряжения в жидкости бывают:
а) только поверхностные; б) только массовые; в) только весовые; г) только поверхностные и массовые; д) только поверхностные и весовые; е) только массовые и весовые; ж) массовые, поверхностные и весовые.
Ответ: г).
3.4. Массовые напряжения имеют размерность:
а) Н/м 2 ; б) Па×с; в) м/с 2 ; г) кг/м 3 ; д) Н/кг; е) Па/кг.
Ответ: в), д).
3.5. Поверхностные напряжения по отношению к рассматриваемому участку поверхности принято раскладывать на:
а) нормальные и ортогональные; б) нормальные и касательные; в) вязкие и тангенциальные; г) нормальные и тангенциальные; д) тангенциальные и массовые.
Ответ: б) или г).
3.6. Поверхностные напряжения имеют размерность:
а) Н/м 2 ; б) Па×с; в) м/с 2 ; г) кг/м 3 ; д) Н/кг; е) Па/кг.
Ответ: а).
3.7. Нормальные напряжения считаются положительными, если они:
а) сжимают жидкость; б) растягивают жидкость; в) сдвигают один слой жидкости относительно другого.
Ответ:б).
3.8. Давление в жидкости – это нормальное напряжение, взятое с обратным знаком. Оно:
а) сжимает жидкость; б) растягивает жидкость; в) сдвигает один слой жидкости относительно другого.
Ответ:а).
3.9. Поверхностное напряжение в жидкости является:
а) скалярной величиной; б) векторной величиной; в) тензорной величиной.
Ответ:в).
3.10. Значение гидростатического давления в любой точке жидкости:
а) не зависит от направления; б) зависит от направления; в) больше со стороны свободной поверхности жидкости; г) меньше со стороны свободной поверхности жидкости; д) больше со стороны увеличения глубины.
Ответ:а).
3.12. Гидростатическое давление в любой точке жидкости:
а) тем меньше, чем больше плотность жидкости; б) тем больше, чем больше плотность жидкости; в) не зависит от плотности жидкости.
Ответ:б).
3.13. Если давление в какой-то точке жидкости увеличилось, то в любой другой точке жидкости давление:
а) увеличится на столько же; б) увеличится в 9,81 раза; в) уменьшится на столько же; г) уменьшится в 9,81 раза; д) останется неизменным.
Ответ:а).
3.14. В любой точке покоящейся в поле силы тяжести жидкости давление:
а) увеличивается вдоль ускорения свободного падения; б) не зависит от направления; в) увеличивается в направлениях перпендикулярных ускорению свободного падения; г) уменьшается в направлениях перпендикулярных ускорению свободного падения; д) увеличивается в направлении, противоположном напра-влению ускорению свободного падения.
Ответ:а).
3.15. Для жидкости, покоящейся в поле силы тяжести, давление в любой ее точке определяется:
а) поверхностным натяжением; б) значением ускорения свободного падения; в) значением вязкости жидкости; г) значением модуля упругости жидкости; д) значением ускорения свободного падения и плотностью жидкости
Ответ:д).
3.16. Основное уравнение гидростатики в дифференциальной форме 
а) увеличивается с удалением от центра Земли; б) не изменяется при удалении от центра Земли; в) уменьшается с удалением от центра Земли.
Ответ:в).
3.17. Основное уравнение гидростатики в дифференциальной форме имеет вид:

Ответ:б).
3.18. Чтобы проинтегрировать основное уравнение гидростатики в дифференциальной форме необходимо иметь зависимость:
а) плотности от давления; б) зависимость плотности от ускорения свободного падения; в) зависимость давления от ускорения свободного пааадения; г) нет необходимости иметь какую-либо зависимость.
Ответ:а).
3.19. Интегрирование основного уравнения гидростатики дает возможность определить:
а) значение давления в зависимости от плотности; б) значение давления в зависимости от высоты положения; в) значение ускорения свободного падения в зависимости от высоты положения.
Ответ:б).
3.20. Ось Z координат направлена противоположно ускорению свободного падения. Как изменяется гидростатическое давление в жидкости в направлении оси Y?
а) увеличивается; б) уменьшается; в) остается неизменным.
Ответ:в).
3.21. Ось Z координат направлена противоположно ускорению свободного падения. Как изменяется гидростатическое давление в жидкости в направлении оси X?
а) увеличивается; б) уменьшается; в) остается неизменным.
Ответ:в).
3.22. Ось Z координат направлена противоположно ускорению свободного падения. Как изменяется гидростатическое давление в жидкости в направлении оси Z?
а) увеличивается; б) уменьшается; в) остается неизменным.
Ответ:б).
3.23. Ось Z координат направлена вдоль ускорения свободного падения. Как изменяется гидростатическое давление в жидкости в направлении оси Y?
а) увеличивается; б) уменьшается; в) остается неизменным.
Ответ:в).
3.24. Ось Z координат направлена вдоль ускорения свободного падения. Как изменяется гидростатическое давление в жидкости в направлении оси X?
а) увеличивается; б) уменьшается; в) остается неизменным.
Ответ:в).
3.25. Ось Z координат направлена вдоль ускорения свободного падения. Как изменяется гидростатическое давление в жидкости в направлении оси Z?
а) увеличивается; б) уменьшается; в) остается неизменным.
Ответ:а).
3.26 Основное уравнение гидростатики для несжимаемой жидкости таково:

Ответ:а).
3.27. В основном уравнении гидростатики для несжимаемой жидкости вертикальная координата h представляет:
а) высоту расположения рассматриваемой точки в жидкости; б) глубину погружения; в) координату наблюдателя; г) координату свободной поверхности.
Ответ:б).
3.28. В основном уравнении гидростатики для несжимаемой жидкости величина p0 представляет:
а) нулевое давление; б) давление в начале отсчета координаты z; в) да-вление на свободной поверхности жидкости.
Ответ:в).
3.28. Основной закон гидростатики формулируется так:
а) давление в жидкости увеличивается с глубиной погружения по линейному закону; б) давление в жидкости увеличивается с глубиной погружения по параболическому закону; в) с глубиной погружения давление не изменяется; г) давление в жидкости уменьшается с глубиной погружения по линейному закону; д) давление в жидкости уменьшается с глубиной погружения по параболическому закону.
Ответ:а).
3.29. Манометрическое давление:
а) это разность между абсолютным и атмосферным давлением; б) это разность между атмосферным и абсолютным давлением; в) это разность между давлением на свободной поверхности жидкости и на глубине погружения.
Ответ:а).
3.30. Вакуумметрическое давление:
а) это разность между абсолютным и атмосферным давлением; б) это разность между атмосферным и абсолютным давлением; в) это разность между давлением на свободной поверхности жидкости и на глубине погружения.
Ответ:б).
3.31. При относительном равновесии жидкости давление в любой ее точке зависит от:
а) ускорения жидкости; б) от скорости равномерного движения жидкости; в) от формы сосуда, в котором движется жидкость.
Ответ:а).
3.31. При вращении жидкости в сосуде давление в жидкости:
а) изменяется только в вертикальном направлении; б) изменяется только в радиальном направлении; в) зависит и от радиальной, и от осевой координаты рассматриваемой точки в жидкости.
3.32. Плавание тела обусловлено действием:
а) только массовых сил; б) только поверхностных сил; в) результирующей поверхностных и массовых сил.
Ответ:в).
3.33.Уравнение основного закона гидростатики для сжимаемой жидкости имеет вид:
а) 



Ответ:д).
3.34. Массовое напряжение в жидкости является:
а) скалярной величиной; б) векторной величиной; в) тензорной величиной.
Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Основы гидравлики
Видео:Основы гидродинамики и аэродинамики | основное уравнение гидростатики | для взрослыхСкачать

Гидростатика и ее законы
Гидростатика – раздел гидравлики, в котором изучаются законы равновесия жидкостей, находящихся в покое.
Понятие покоя или равновесного состояния по отношению к жидкости можно отождествлять с аналогичным понятием в одном из разделов технической механики — статике. Любое тело, материальная точка или обособленный объем вещества (в т. ч. жидкости) считается покоящимся, если все силы (внешние и реактивные), действующие на этот материально существующий субъект (т. е. имеющий массу), уравновешивают друг друга.
Тем не менее, жидкость по своим свойствам и «способностям» уникальна, поэтому гидростатика призвана пояснить некоторые особенности поведения жидкого вещества в тех или иных условиях.
Гидростатическое давление
На жидкость, находящуюся в покое действуют массовые и поверхностные силы. Массовыми являются силы, действующие на все частицы рассматриваемого объема жидкости. Это силы тяжести и силы инерции (силы инерции проявляются в движущейся жидкости, поэтому их учитывает раздел гидродинамика) .
Массовые силы пропорциональны массе жидкости, а для однородной жидкости, плотность которой одинакова во всех точках, — объему. Поэтому массовые силы называют еще объемными.
К поверхностным относятся силы, действующие на поверхности жидкости. Это, например, атмосферное давление, действующее на жидкость в открытом сосуде, или силы трения, возникающие в движущейся жидкости между отдельными слоями и стенками сосуда (в покоящейся жидкости силы трения отсутствуют) .
Жидкость, находящаяся в состоянии покоя, может находиться только под действием силы тяжести и поверхностных сил, вызванных внешним давлением (например, атмосферным) . Внешние силы давления являются нормальными сжимающими поверхностными силами (считается, что жидкость не сопротивляется растяжению) . Все эти силы создают в неподвижной жидкости некоторую равнодействующую (результирующую) силу, которая называется гидростатической силой .
Покоящаяся жидкость под воздействием гидростатической силы находится в напряженном состоянии, характеризуемом гидростатическим давлением.
Выделим в покоящейся жидкости произвольный объем (см. рис. 1) . Мысленно разделим этот объем произвольной плоскостью П . Выделим на полученном сечении точку А и некоторую площадку ΔS вокруг этой точки.

Отношение гидростатической силы к площади поверхности (выделенного сечения) жидкости называют средним гидростатическим давлением. Истинное гидростатическое давление в данной точке жидкости может быть определено, как предел, к которому стремится среднее гидростатическое давление при бесконечном уменьшении рассматриваемой площадки ΔS :
p = lim ΔP/ΔS при ΔS стремящемся к нулю.
Гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует, и величина его в произвольной точке не зависит от ориентации этой площадки в пространстве.
Это утверждение вытекает из условий:
— неподвижности жидкости, поскольку при любом перемещении жидкости неизбежно возникают касательные напряжения;
— равновесия рассматриваемого элементарного (бесконечно малого) объема, поскольку равновесие может быть достигнуто лишь при равенстве всех действующих на рассматриваемый элементарный объем внешних сил (предполагается, что весом бесконечно малого объема жидкости можно пренебречь) .
При этом выделенный объем может иметь любую произвольную форму – куба, правильной пирамиды и т. д. – в любом случае легко доказать, что силы, действующие на грани этого объема будут одинаковы во всех направлениях.
Основное уравнение гидростатики. Закон Паскаля.
Выделим в однородной жидкости, находящейся в покое, элементарный объем ΔV в виде прямоугольного параллелепипеда с площадью горизонтального основания ΔS и высотой H (см. рис. 2) .
Рассмотри условия равновесия выделенного элементарного объема.
Пусть давление на плоскость верхнего основания равно р1 , а на плоскость нижнего основания – р .
Силы давления действующие на вертикальные грани выделенного параллелепипеда взаимно уравновешиваются как равные по величине и противоположно направленные.
На горизонтальные грани действуют силы давления, направленные вертикально: на верхнюю грань эта сила будет равна р1ΔS (направлена вниз) , на нижнюю – pΔS (направлена вверх) .
На верхнюю и нижнюю грани рассматриваемого параллелепипеда действуют силы, обусловленные давлением на жидкость со стороны внешней среды (например, атмосферного давления) и вес (сила тяжести) элементарного столбика жидкости над каждой из горизонтальных граней параллелепипеда.
Очевидно, что разность сил тяжести, действующих на верхнюю и нижнюю площадку, будет равна весу жидкости, заключенной в объеме рассматриваемого параллелепипеда, который равен ρgΔV ,
где ρ – плотность жидкости, g – ускорение свободного падения, ΔV – объем параллелепипеда: ΔV = HΔS .
Исходя из условия равновесия выделенного элементарного параллелепипеда объемом ΔV , можно утверждать, что сумма всех внешних сил, действующих на параллелепипед равна нулю, т. е.:
pΔS – p1ΔS – ρgΔV = pΔS – p1ΔS – ρgΔSH = 0 .
Преобразовав эту формулу, получим величину гидростатического давления на нижнюю горизонтальную площадку:
Если верхняя грань параллелепипеда граничит с внешней средой (например, атмосферой) , оказывающей давление р0 на жидкость, то формула может быть переписана в виде:
Это выражение является основным уравнением гидростатики .
Итак, гидростатическое давление в любой точке внутри покоящейся жидкости равно сумме давления на свободную поверхность со стороны внешней среды и давления столба жидкости высотой, равной глубине погружения точки (т. е. ее расстоянию от свободной поверхности жидкости) .
На основании основного уравнения гидростатики может быть сформулирован закон Паскаля: внешнее давление, производимое на свободную поверхность покоящейся жидкости, передается одинаково всем ее точкам по всем направлениям.
Блез Паскаль (Blaise Pascal, 1623 — 1662) — выдающийся французский ученый — математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.
Любопытны цитаты из популярного сборника высказываний Паскаля, не потерявшие актуальность и в наши дни.
Вот некоторые из них:
- Искание истины совершается не с весельем, а с волнением и беспокойством; но все таки надо искать ее потому, что, не найдя истины и не полюбив ее, ты погибнешь.
- Прошлое и настоящее — наши средства, только будущее — наша цель.
- Нас утешает любой пустяк, потому что любой пустяк приводит нас в уныние.
- Когда человек пытается довести свои добродетели до крайних пределов, его начинают обступать пороки.
- Справедливость должна быть сильной, а сила должна быть справедливой.
- Истина так нежна, что чуть только отступил от нее, впадаешь в заблуждение, но и заблуждение это так тонко, что стоит только немного отклониться от него, и оказываешься в истине.
- Величие не в том, чтобы впадать в крайность, но в том, чтобы касаться одновременно двух крайностей и заполнять промежуток между ними.
- Изучая истину, можно иметь троякую цель: открыть истину, когда ищем ее; доказать ее, когда нашли; наконец, отличить от лжи, когда ее рассматриваем.
- Сила добродетели человека должна измеряться не его усилиями, а его повседневной жизнью.
- Лишь в конце работы мы обычно узнаём, с чего нужно было её начать.
- Существует достаточно света для тех, кто хочет видеть, и достаточно мрака для тех, кто не хочет.
- Человек — это приговорённый к смерти, казнь которого откладывается на время его жизни.
Умер Паскаль после тяжелой и продолжительной болезни в возрасте 39 лет, оставив после себя яркий след в науке.
Имя этого ученого увековечено в названиях одной из единиц международной системы СИ, языка программирования Paskal и лунного кратера.
Пример решения задачи с использованием закона Паскаля
Водолазы при подъеме затонувшего судна работали на глубине 50 м. Определить давление p воды на этой глубине и силу P давления на скафандр водолаза, если площадь его поверхности S равна 1 м 2 .
Атмосферное давление считать равным 1013 МПа (0,1013×106 Па), плотность воды – 1000 кг/м 3 .
Решение:
Определим давление, оказываемое столбом воды на глубине 50 м (в Па) :
ρgH = 1000×9,81×50 = 4,9×105 Па.
Применив основное уравнение гидростатики, с учетом атмосферного давления, найдем давление на глубине 50 м:
p = p0 + ρgH = 1,013×105 + 4,9×105 = 5,91×105 Па ≈ 0,59 МПа.
Силу давления столба воды на скафандр водолаза определим по формуле:
P = pS = 5,91×105×1 = 591000 Н = 591 кН.
Основное уравнение гидростатики и закон Паскаля широко применяются при решении многих инженерных задач. Свойства жидкости передавать производимое на нее давление без изменения используется при конструировании гидравлических прессов, домкратов, гидроаккумуляторов, гидроприводов и других механизмов. Основной принцип работы этих устройств основа на пропорциональной разности сил, приложенных к поршням гидроцилиндров, имеющих разный диаметр: P1S2 = P2S1 .
Видео:Основное уравнение гидростатики (задачи)Скачать

Основное уравнение гидростатики для несжимаемой жидкости таково
Часть 1 МЕХАНИКА
3.1. Основные уравнения гидростатики
Хотя по своим свойствам жидкости и газы во многом отличаются друг от друга, существует общее свойство, что объединяет их, — текучесть, то есть их малое сопротивление к деформации сдвига. Следовательно, исследуя движение жидкостей и газов, используем единый подход. Раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми твердыми телами, называют гідроаеромеханікою.
В гідроаеромеханіці пренебрегают молекулярным строением жидкостей и газов, воспринимая их как сплошная среда, непрерывно распределенный в пространстве. Плотность жидкостей и газов в общем случае зависит от давления. Однако во многих задачах этой зависимостью можно пренебречь и пользоваться единым понятием несжимаемой жидкости — жидкости, плотность которой всегда постоянная и не зависит от времени.
Если в неподвижной жидкости поместить тонкую пластину, то частицы жидкости, которые размещаются с разных сторон от нее, будут действовать на каждый ее элемент Δ s с силами Δ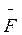
Физическую величину, равную отношению нормальной силы, действующей со стороны жидкости на любую плоскость, к ее площади, называют давлением жидкости р:
Единица давления — паскаль (Па): один паскаль равен давлению, которое создает сила в один ньютон, равномерно распределенная по нормальной к ней поверхности площадью 1 м 2
Для жидкости, находящейся в равновесии, выполняется закон Паскаля: давление в жидкости или газе передается во всех направлениях одинаково.
Рассмотрим, как влияет сила тяжести на распределение давления внутри неподвижной несжимаемой жидкости, находящейся в покое. Условно выделим в жидкости элемент определенной формы, например параллелепипед, площадь основания которого Δ s , а высота h (рис. 3.2). Поскольку жидкость этого объема находится в покое, то равнодействующая всех сил, действующих на объем жидкости, равна нулю, а силы, действующие на боковую поверхность, взаимно уравновешиваются. Чтобы найти условия равновесия параллелепипеда в вертикальном направлении, надо учесть давления р1 и г2, действующих на верхнюю и нижнюю основы параллелепипеда. Запишем условие равновесия для вертикального направления:
где ρ gh — гидростатическое давление жидкости, обусловлен действием земного притяжения; ρ — плотность жидкости.
Уравнение (3.2) является основным уравнением гидростатики для несжимаемой жидкости.
Гидростатическое давление жидкости зависит от плотности жидкости ρ и высоты ее столба и не зависит от формы сосуда, в котором хранится жидкость. Следовательно, если давление на свободную поверхность неподвижной жидкости ρ 0 , то гидростатическое давление на глубине h определяют уравнением (3.2).
Согласно этого уравнения сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, которая равна весу вытесненной телом жидкости (газа):
где F А — сила Архимеда; ρ — плотность жидкости; V — объем погруженного в жидкость тела.
Для измерения гидростатического давления применяют манометры. Самый простой тип манометра имеет вид U -образной трубки, один конец которой соединяется с сосудом, в котором измеряется давление, второй — с атмосферой или запаян и воздух из него откачан. По разнице уровней жидкостей в коленах манометра определяют давление в сосуде.
Большие давления измеряют металлическими манометрами, в которых металлическая упругая трубка присоединяется к резервуару, где измеряется давление. При изменении давления изменяется конфигурация трубки. Ее изменение фиксируется стрелкой или другим показателем давления. Низкие и высокие давления измеряют приборами, действие которых основано на зависимости электрического сопротивления манганінової дротини от давления или электрических свойств кварцевых пластинок от давления (пьезоэлектрический эффект).
Манометры состоят из чувствительного элемента и элемента, который давление превращает в другую величину, удобную для измерения. По типу чувствительного элемента манометры разделяют на жидкостные, механические, поршневые, электрические, тепловые, радиоактивные и т.д.
📹 Видео
Основной закон гидростатикиСкачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Гидростатическое давлениеСкачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

ОСНОВНЫЕ ЗАКОНЫ ГИДРОСТАТИКИСкачать

Закон БернуллиСкачать

Следствие из основного уравнения гидравлики: закон ПаскаляСкачать

Лекция 15 | Механика | Введение в гидродинамику и гидростатику несжимаемой жидкостиСкачать

Урок 47 (осн). Расчет давления жидкости на дно и стенки сосудаСкачать

Якута А. А. - Механика - Эффект Доплера. Введение в гидро- и аэростатику. Закон АрхимедаСкачать

Урок гидравлики - 01 - Основные положенияСкачать

Уравнение Бернулли гидравликаСкачать

Гидростатика c нуля за 30 минут | Физика, Пенкин, подготовка к ЕГЭ, ОГЭ | 7, 8, 9, 10, 11 классСкачать

Гидравлика лекция 2Скачать








