Основное уравнение эйлера для турбомашин (8 видео)

Основное уравнение турбомашин (уравнение Эйлера) и его анализ

Теоретическая работа, сообщенная 1 кг газа (напор), Дж/кг, при изоэнтропном (адиабатном) сжатии его от давления Р₁ до давления Р₂ может быть вычислена по известному из термодинамики соотношению (6.2):

= .

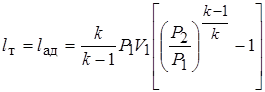
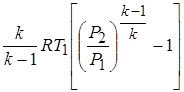
Эта же работа может быть найдена из уравнения Эйлера:

, (6.19)

где u₂ и u₁ – окружные скорости концов рабочих лопаток, м/с; с₂_u и c₁_u – окружные составляющие абсолютных скоростей потока на выходе и входе рабочего колеса (см. рис. 6.2).

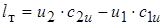
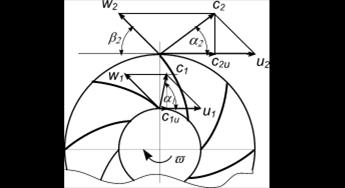
Рис. 6.2. Треугольники скоростей газового потока на входе и выходе рабочего колеса центробежного компрессора (ЦБК)

Используя соотношения для треугольников скоростей, преобразуем уравнение Эйлера. В соответствии с теоремой косинусов из выходного треугольника можно записать:

, где ,

. (6.20)

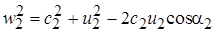
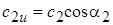
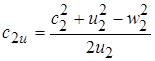
Аналогично из входного треугольника:

. (6.21)

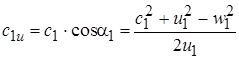
Подставив эти выражения в уравнение Эйлера (6.19) получим:

. (6.22)

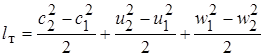
Это преобразованное уравнение Эйлера, удобное для анализа. Здесь два последних члена выражают часть работы ТК, затраченной на прирост давления газа в рабочем колесе. Это статический напор колеса. Первый член – это динамический напор колеса, который может быть преобразован в статический напор в диффузоре ТК.

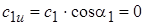
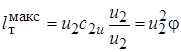
Из уравнения (6.19) видно, что максимальный напор, а следовательно, максимальное давление, развиваемое ступенью ТК, будут при , т.е. при a₁=90° (вход потока в колесо без предварительной закрутки): . Иначе

, (6.23)

где 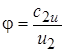– коэффициент закрутки потока, который является характеристикой геометрии рабочего колеса. Отсюда важный вывод:

· при постоянном значении j (для одного и того же колеса), напор (удельная работа сжатия) развиваемый компрессором пропорционален квадрату частоты вращения колеса.

Максимальная окружная скорость u₂ лимитируется условиями прочности. В стационарном компрессоростроении при загнутых рабочих лопатках для применяемых материалов обычно принимают u₂@250 м/с. В таких ступенях ЦБК степени повышения давления составляют e_ст=1,3-1,5.

На практике в ЦБК могут быть использованы рабочие колеса с лопатками следующих форм (см. рис. 6.3):

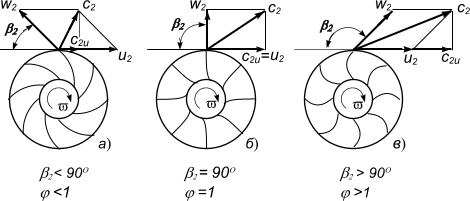Основное уравнение эйлера для турбомашин

Рис. 6.3. Схемы рабочих колес ЦБК: а – лопатки загнуты назад; б – лопатки радиальные; в – лопатки загнуты вперед

В соответствии с (6.23), если все три колеса одного диаметра, то при неизменной частоте вращения (u₂=const) и одинаковых условиях входа потока наименьший напор будет в колесе а) и наибольший – в колесе в).

Преобразование кинетической энергии потока в потенциальную происходит в диффузоре и обратном направляющем аппарате. Оно сопровождается значительными газодинамическими потерями. Эти потери растут с увеличением скорости c₂ (в соответствии с законом Дарси). Отсюда области применения центробежных компрессоров с разными типами колес:

1) в стационарных крупных компрессорах, для которых экономичность имеет первостепенное значение, используют рабочие колеса с лопатками, загнутыми назад (b₂_л=35-55°);

2) загнутые вперед лопатки применяют в тех случаях, когда необходимо получить высокий напор в одной ступени, а величина КПД играет второстепенную роль;

3) наиболее прочные – радиальные лопатки. Они позволяют получать окружную скорость до 500 м/с. Кроме того, эти лопатки обеспечивают максимальную диффузорность, т.е. наибольший член уравнения (6.22): .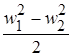

Благодаря этому в одном колесе с радиальными лопатками достижимы более высокие статические давления. Такие колеса применяются тогда, когда требуются высокие давления при минимальных габаритах и массе. Обычно в транспортных конструкциях.

В осевых компрессорах (ОК) обычно u₁=u₂, т.е. в уравнении (6.22) отсутствует член 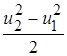, отражающий влияние центробежных сил.

Вследствие этого ступень ОК развивает значительно меньший напор, чем ступень ЦБК. Так что при равных степенях повышения давления и других равных условиях ОК имеет значительно большее число ступеней, чем ЦБК.

Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Лекция на тему: Характеристики турбомашин. Уравнения Эйлера

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: : Характеристики турбомашин. Уравнения Эйлера.

1. Теоретические характеристики турбомашин

2. Действительные индивидуальные характеристики центробежных и осевых турбомашин

1. Хаджиков Р.Н., Бутаков С.А. Горная механика. — М.: Недра, 1982. (стр. 11-17)рис. 5 и 7.

1. Теоретические характеристики турбомашин .

Теоретическая подача центробежной турбомашины получается как произведение площади выходного живого сечения πD₂b₂ рабочего колеса без учета стеснения его лопастями на радиальную скорость с_2r-проекцию скорости с₂ на направление радиуса:

где b₂— ширина рабочего колеса на выходе;

D₂ – диаметр рабочего колеса;

c_2r – радиальная скорость движения жидкости из колеса.

В осевой турбомашине выходное сечение потока равно площади, ометаемой лопастями, а теоретическая производительность турбомашины — произведению этой площади на осевую скорость с _, представляющую собой проекцию скорости с на осевое направление:

Q_T=c .

где D₂— диаметр рабочего колеса;

d_ВТ — диаметр втулки.

Теоретическая индивидуальная характеристика турбомашины представляет собой зависимость между теоретическим напором Н_Т и теоретической подачей Q_Т при известных размерах турбомашины и определенной частоте вращения ее рабочего колеса.

Зависимость H_T=f (Q_T) получается следующим образом:

На основании этого выражения и формулы

C_2u=U₂+ ctg β₂ _.

Подставляя значение С_2u в формулу Н_Т= получаем уравнение теоретической индивидуальной характеристики центробежной турбомашины:

Н_т=

Применительно к осевым турбомашинам:

Н_т=

где β-угол притекания потока на выходе.

Лопасти рабочих колес центробежных турбомашин могут быть:

1) загнутые вперед, когда β₂ 0 (рис. 2, а);

2) радиальные, когда β₂ = 90°, т. е. ctg β = 0 (рис. 2, б);

3) загнутые назад, когда β₂ > 90°, т. е. ctg β₂

В соответствии с этим и на основании выражения Н_т= в коорди натных осях подачи Q_T и напора Н_т (рис. 2) строят теоретические индивидуальные характеристики турбомашины при u₂ = const. При Q_T =0 для всех типов рабочих колес

Н_т= .

Из рис. 2 видно, что при увеличении подачи Q_T напор турбо машин с колесами, имеющими лопасти, загнутые вперед, возра стает, при радиальных лопастях остается постоянным, а при лопастях, загнутых назад, снижается.

В отношении величины напора колеса с лопастями, загнутыми вперед, предпочтительнее. Однако в этих колесах имеет место наибольшая скорость с_{2 ,} а наименьшая величина ее – в колесах с лопастями, загнутыми назад. Для уменьшения потерь желательно, чтобы скорость с₂ была меньше, но не менее известного предела , так как с ее уменьшением снижается Н_Т. Значения с₂ , обеспечивающие максмальный к. п. д. колеса, имеют место при 155 о >β₂>130 о , поэтому необходимо иметь колесо большого диаметра. Центробежные вентиляторы имеют одно колесо (в целях сокра щения габаритов вентилятора по оси вращения его вала). В центро бежных вентиляторах небольшой производительности применя ются колеса с лопастями, загнутыми вперед. При этом несколько снижается к. п. д., что в известной степени компенсируется при менением диффузора. В вентиляторах большой производительности применяются рабочие колеса с лопастями, загнутыми назад, которые обеспечивают более высокий к. п. д.

Рис. 2. Рабочие колеса центробежных турбомашин и соот ветствующие им теоретические индивидуальные характери стики

Шахтные насосы по сравнению с вентиляторами характери зуются значительными напорами и небольшими подачами. По этому центробежные насосы обычно имеют несколько последова тельно соединенных колес относительно небольших диаметров. Для насосов применяются колеса с лопастями, загнутыми назад. Та кого же типа колеса применяются для центробежных компрес соров.

Теоретическая индивидуальная характеристика осевой тур бомашины по формуле (18) в координатах Q_T — Н_т имеет вид нисходящей прямой.

Действительная индивидуальная харак теристика турбомашины представляет собой зависи мость между действительным напором Н и действительной по дачей Q турбомашины при известных размерах машины и опре деленной частоте вращения рабочего колеса. Действительный на пор меньше теоретического из-за потерь в турбомашине, причинами которых являются: 1) конечное число лопастей колеса; 2) трение частиц жидкости между собой и о поверхности проточной части турбомашины; 3) затраты энергии на удары при вихревом движе нии жидкости внутри турбомашины; 4) затраты энергии на преоб разование скоростного напора в статический.

В реальной турбомашине с известным числом лопастей определенной толщины скорости движения жидкости по сечению данного радиуса различны; давление у лицевой стороны лопасти выше, чем у тыльной; поток жидкости на выходе из колеса скошен в сторону, обратную направлению вращения.

Рис. 3. Движение жидкости в межлопастном канале (а, б) и скорости на выходе из колеса при конечном числе лопастей (в)

Опыты ЦАГИ показали, что при подаче турбомашины меньше нормальной поток (рис. 3, а) прижимается к лицевой стороне 1 лопасти центробежного колеса, а у ее тыльной стороны 2 обра зуется завихренная зона 3. При очень малой подаче поток пере текает из одного канала в другой. При большой подаче поток (рис. 3, б) прижимается к тыльной стороне лопасти 2, а у лицевой стороны 1 возникает завихренная зона 3. Оторвавшаяся при входе в канал от лицевой стороны лопасти часть потока скашивается на выходе в сторону, обратную направлению вращения. Вихревая з она оказывается замкнутой, так как эта часть потока снова встре чает лицевую сторону лопасти. Поэтому относительная скорость у лицевой стороны лопасти не касательна к лопасти и по величине больше теоретической .

Таким образом, с’_2и — действительная величина окружной проекции абсолютной скорости — меньше теоретической с₂ _u при неизменной радиальной скорости с₂ _r , а создаваемый рабочим ко лесом напор с учетом конечного числа лопастей меньше получен ного по формуле (4), т. е. Н_тк = k _ц H _т . Коэффициент k _ц называется коэффициентом циркуляции.

Рис.4. Формы действительных индивидуальных харак теристик турбомашины:

а и б — центробежных; в — осевой

Все указанные потери напора учитываются гидравли ческим к. п. д. турбомашины, определяемым отношением полезной мощности турбомашины к сумме полезной мощности и мощности, затраченной на потери напора в турбомашине. Гид равлический к. п. д. зависит от качества изготовления турбома шины, ее параметров и равен для современных машин η _Т = 0,8. 0,96.

Действительная подача турбомашины, как и напор, меньше теоретической вследствие объемных потерь — утечек через не плотности в турбомашине. Эти потери характеризует объемный к. п. д. — отношение полезной мощности к сумме полезной мощ ности и мощности, утраченной с утечками. В среднем объемный к. п. д. η _о = 0,95 . 0,98.

В турбомашине имеются также механические потери — за траты энергии на трение в подшипниках, сальниках, жидкости о наружные поверхности дисков рабочего колеса (дисковое трение) и др. Эти потери определяются механическим к. п. д., который для современных турбомашин η _м = 0,95 . 0,99.

Отношение полезной мощности к мощности турбомашины на зывается к. п. д. турбомашины и является ее характеристикой. Он равен произведению гидравлического, объемного и механического к. п. д., т. е. η =η_г η_о η_м.

Кривую действительной индивидуальной характеристики тур бомашины можно получить, если из ординат теоретического на пора Н_т вычесть ординаты потерь напора Н_д при соответствующих подачах (рис. 4).

Сравнение форм действительных индивидуальных характери стик турбомашин, имеющих рабочие колеса с лопастями, загну тыми вперед (рис. 4, а) и назад (рис. 4, 6), показывает, что пер вая характеристика имеет вид выпуклой кривой (горбатые харак теристики), а вторая — падающей кривой (безгорбые характе ристики) или имеет слабо выраженный горб. Форма характери стики при определенных условиях оказывает влияние на устой чивость режима работы турбомашины.

1. Изучение материала конспекта лекций.

2. Г . Н. Хаджиков, Горная механика, М. Недра 1982, стр. 8-10

Составил Ларионов О.Ф. — преподаватель высшей квалификационной категории ГПОУ «Комсомольский индустриальный техникум» , г. Комсомольское, Донецкая область, 2021 год.

Видео:Курс ""Турбомашины". Уравнение моментов количества движения (Эйлера)Скачать

Документы

ТЕЧЕНИЕ ГАЗА В СТУПЕНИ ТУРБОМАШИНЫ

9-1. ОСНОВНЫЕ УРАВНЕНИЯ

В ступени турбомашиньи происходит преобразование потенциальной энергии газа в механическую работу (турбина) или механической работы в потенциальную энергию газа (компрессор). В обоих случаях поток газа совершает энергетический обмен с окружающей средой.

Рассмотрим принципиальную схему ступени турбины с осевым потоком газа. На рис. 9-1 показаны основные элементы такой ступени. По входному патрубку 1 газ подводится к неподвижной направляющей решетке 2, где часть его потенциальной энергии преобразуется в кинетическую энергию. Приобретая в направляющей решетке значительные скорости, поток газа проходит через зазор 3 и попадает на рабочие лопатки 4, укрепленные на колесе 5. Здесь происходит перенос энергии к ротору турбины.

Радиусами г и r+dr проведем два цилиндрических сечения, ось которых будет совпадать с осью турбины. Этими сечениями выделим элементарную ступень турбины; развертывая ее на плоскость (рис. 9-2,а), можно проследить характер изменения скоростей в проточной части ступени 114 .

Введем в отличие от предыдущего следующие обозначения скоростей:

с — скорость абсолютного движения газа; скорость газа в относительном движении;

Рис. 9-1. Схема ступени турбины в осевом потоке газа (а) и распределение параметров торможения, статических давлений и скоростей •в проточной части (б).

¦ скорость переносного движения (окружная скорость); и w_и — проекции ско

ростей абсолютного и относительного потоков на направление скорости и;

— проекции скоростей абсолютного и относительного потоков на направление оси вращения;

.,w — радиальные составляющие скоростей абсолютного и относительного потоков.

Индексом 1 обозначим скорости, относящиеся ко

входу, a индек!сол^ 2 — к выходу из рабочих лопаток.

Рабочий процесс ступени турбины можно (проследить по рис. 9-1 и 9-2. В межлопаточных каналах направляющей решетки поток газа ускоряется и одновременно поворачивается, покидая ее со скоростью с, направленной под углом си к оси решетки (рис. 9-2,а). При этом ло-6П2.2 Дейч Михаил Ефимович

Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л.

с черт. и илл. 6П2.2

Редактор Б. Я¦ Шумяцкий Техн. редактор А. М. Фридкин

ТЕЧЕНИЕ ГАЗА В СТУПЕНИ ТУРБОМАШИНЫ

9-1. ОСНОВНЫЕ УРАВНЕНИЯ

Рассмотрим принципиальную схему ступени турбины с осевым потоком газа. На рис. 9-1 показаны основные элементы такой ступени. По входному патрубку 1 газ подводится к неподвижной направляющей решетке 2, где часть его потенциальной энергии преобразуется в кинетическую энергию. Приобретая в направляющей решетке значительные скорости, поток газа проходит через зазор 3 и попадает на рабочие лопатки 4, укрепленные на колесе 5. Здесь происходит перенос энергии к ротору турбины.

Радиусами г и r+dr проведем два цилиндрических сечения, ось которых будет совпадать с осью турбины. Этими сечениями выделим элементарную ступень турби-ньи; развертывая ее на плоскость (рис. 9-2,а), можно проследить характер изменения скоростей в проточной части ступени 115 .

Введем в отличие от предыдущего следующие обозначения скоростей:

с — скорость абсолютного движения газа; w — скорость газа в относительном движении; и — скорость переносного движения (окружная скорость); проекции скоростей абсолютного и относительного потоков на направление скорости и;

Рис. 9-1. Схема ступени турбины в осевом потоке газа (а) и распределение параметров торможения, статических давлений н скоростей ¦в проточной части (б).

проекции скоростей абсолютного и относительного потоков на направление оси вращения;

радиальные составляющие скоростей абсолютного и относительного потоков.

Индексом 1 обозначим скорости, относящиеся ко

входу, а индекйоА^ 2 — к выходу из рабочих лопаток.

Рабочий процесс ступени турбины можно проследить по рис. 9-1 и 9-2. В межлопаточных каналах направляющей решетки поток газа ускоряется и одновременно поворачивается, покидая ее со скоростью с_ь направленной под углом си к оси решетки (рис. 9-2,а). При этом ло-генциальная энергия газа преобразуется в кинетическую энергию потока.

На рабочие лопатки поток входит с относительной скоростью wI, которую легко получить, ‘построив входной треугольник скоростей.

В межлопаточных каналах рабочей решетки происходи? поворот потока в относительном движении; при

Рис. 9-2. Развертка проточной части (а) и треугольники скоростей осевой ступени (б).

этом силы давления газа производят работу вращения ротора турбины. Поток выходит из рабочих лопаток с относительной скоростью w₂ под углом Рг к оси решетки. Зная окружную скорость и, легко построить выходной треугольник скоростей и определить скорость абсолютного потока на выходе из ступени с₂ (рис. 9-2,а). Часто входной и выходной треугольники скоростей изображают из одного полюса, как показано на рис. 9-2,6.

Таким образом, энергия газа передается к ротору турбины благодаря тому, что силы давления три повороте потока на лопатках производят работу вращения ротора. В результате температура и давление торможения абсолютного потока уменьшаются так, что

‘ Характерной особенностью рассмотренного процесса является его ступенчатый характер: потенциальная энергия вначале преобразуется 1 кинетическую энергию движущегося газа, а затем на рабочем колесе кинетическая энергия преобразуется в механическую работу. Такой процесс в чистом виде имеет место в активной ступени: статические давления на входе и выходе из рабочей решетки примерно одинаковы, а скорости Wi и W2 различаются только за счет потерь в рабочей решетке.

В чисто реактивной ступени оба составляющих процесса протекают одновременно на рабочем колесе. Поток газа в рабочих каналах в относительном движении ускоряется и одновременно совершает работу вращения ротора. Широкое применение находят промежуточные типы ступеней, в которых рационально сочетаются оба принципа — активный и реактивный. В этом случае преобразование потенциальной энергии газа в кинетическую осуществляется частично в неподвижной решетке и частично в рабочих каналах.

Изменение статических параметров потока и параметров торможения в проточной части такой ступени показано на рис. 9-1,1.

Ступень может быть выполнена также с радиальным потоком газа. В такой ступени газ движется в радиальных плоскостях от оси вращения к периферии или, наоборот, к оси вращения. Радиальная ступень может бьить активного, реактивного или промежуточного типа.

Схемы проточньих частей ступеней турбины с радиальным потоком газа показаны на ри,с. 9-3. В радиальном сечении видны формы профилей направляющей и рабочей решеток ступени и треугольники скоростей на входе и выходе из рабочих каналов. Заметим, что в радиальной ступени окружная скорость меняется от входного к выходному сечению решетки.

В некоторых ступенях поток газд направлен поя углом к оси вращения. При этом радиальные составляющие скорости с_г не равны нулю и при анализе свойств потока должны учитываться (рис. 9-4).

В ступени компрессора (осевого или центробежного) происходит преобразование механической работы в по-

Рис. 9-3. Схемы центробежной (а) и центростремительной (б) радиальных ступеней турбины.

тенциальную энергию газа Каналы рабочей решетки 1 осевого компрессора — расширяющиеся^(рис. 9-5). Давление газа в относительном движении возрастает, а скорость уменьшается. Этот процесс продолжается в направляющем аппарате 2. Энтальпия полного торможения в абсолютном движении возрастает.

В ступени центробежного компрессора движение газа осуществляется от центра к периферии (рис 9-6), рабочие лопатки колеса 1 образуют расширяющиеся каналы, в которых происходит торможение относительного потока. Сжатие газа может продолжаться в лопаточном диффузоре 2.

В точной постановке задачи течение газа в ступени турбомашины описывается дифференциальными уравнениями пространственного потока — вязкой сжимаемой

»Рис 9-5. Схема и развертка проточной части ступени осевого компрессора.

жидкости. Приближенные решения основываются на уравнениях идеальной сжимаемой жидкости, выведенных в гл. 1.

Рис 9-4 Схема диагональной ступени.

движения, неразрывности и записать в цилиндрической качестве независимых переменных, как и ранее, выбираются: радиус-вектор г полярный угол 0 и аппликата г. Направление оси х совпадает с осью вращения турбины. Тогда система уравнений сохранения в абсолютном установившемся движении

(dpjdt = dcjdt = dcjdt= dcjdt = 0)

при R = e = Z = 0 сводится к уравнениям (1-14) и (1-17а).

Для исследования потока в рабочей решетке основные уравнения идеальной жидкости целесообразно записать для

относительного движения. При этбм используются очевидные соотношения (рис. 9-2):

W a = C a’ W r = C r И W u = C u

где ш — угловая скорость вращения рабочей решетки.

Рис 9-6 Схема ступени центробежного компрессора

После подстановки этих соотношений в уравнения (1-17а) для установившегося относительного движения получим:

Дифференциальное уравнение неразрывности для установившегося относительного потока имеет вид:

Система уравнений движения (1 — 17а) и (1-14) или (9-1) и (9-2) дополняется уравнениями сохранения энергии in изоэнтропического процесса При этом система уравнений, определяющая пространственное установившееся движение идеальной сжимаемой жидкости в ступени турбомашины, является замкнутой

Перейдем теперь к выводу уравнения энергии для струйки газа в проточной части ступени Уравнение энергии может быть записано в параметрах абсолютного или относительного движения В первом случае в уравнение энергии вводятся члены, учитывающие энергетический обмен между потоком и окружающей средой Во втором случае (для относительного потока) необходимо учитывать дополнительные силы, введение которьих позволяет рассматривать относительное движение, так, как если бьи оно было абсолютным Такими дополнительными силами являются кориолисова сила инерции и центробежная сила

Уравнение энергии для абсолютного потока напишем в форме первого начала термодинамики. С учетом сделанных допущений получим:

Здесь L_T — работа, совершаемая газом.

Величина L_r может быть определена с помощью уравнения моментов количества движения. Момент сил, действующих на рабочие лопатки при установившемся движении, будет:

где G — секундный расход газа через решетку.

Умножив М_и на угловую скорость вращения решетки ш, найдем секундную работу или мощность, которой обмениваются лопатки с газовым потоком:

Следовательно, работа, отнесенная к весу протекающего газа, равна:

Уравнение (9-4) получено Эйлером. В дифференциальной форме уравнение Эйлера имеет вид:

Так как в турбине газ совершает работу, то вдоль струйки абсолютного течения d(c_uu) 0. Использовав выражения (9-3) и (9-5), получим дифференциальное уравнение энергии для потока в абсолютном движении:

В соответствии с законом сохранения энергии изменение кинетической и внутренней энергии газа в относительном движении ,равно количеству подведенного («ли отведенного) тепла и работе действительных и дополнительных сил. Так как кориолисова сила инерции натравлена нормально к оси струйки в относительном движении (к вектору w), то работа этой силы равна нулю.

Таким образом, из числа дополнительных сил в уравнение анергии для потока газа в относительном движении необходимо ввести центробежную силу, направленную вдоль радиуса нормально к оси вращения. В частном случае аксиальной ступени вектор центробежной силы нормален к линиям тока и работа центробежных сил также равна нулю.

Уравнение энергии для потока в относительном движении получаем на основании первого начала термодинамики (9-3).

Учитывая, что = с_т с*_а— с и используя связь между абсолютными и относительными скоростями, преобразуем выражение (9-6). Получим:

Интегрирование уравнения энергии (9-6) для потока в абсолютном движении дает:

Интеграл уравнения энергии потока в относительном движении (9-7) равен:

Переход от уравнения (9-8) к уравнению (9-9), очевидно, совершается с помощью формулы (рис. 9-2,6)

Полученные уравнения для относительного движения могут быть использованы для расчета ступени не только турбины, но и других турбомашин (компрессор, вентилятор). Направление энергетического обмена (отвод или подвод механической работы) при этом не имеег значения. Это замечание вполне справедливо только в предположении изоэнтропического течения в ступени турбо-машиньв. В реальных условиях движение газа сопровождается потерями. При этом направление энергетического обмена существенно влияет на структуру потока (на характер распределения параметров в проточной части), а следовательно, и на к. п. д. ступени.

При отсутствии потерь изменение состояния газа в абсолютном и относительном движении подчиняется изоэнтропическому закону, который для идеального газа может бьпь представлен формулой p/p K =const.

В этом случае интегралы уравнений количества движения и энергии совпадают. Действительно, для одномерного потока в абсолютном движении уравнение импульсов имеет вид: ^

Считая относительное движение газа в ступени установившимся, запишем уравнение импульсов в такой форме:

wdw— по 2 cos (r,x) dx — 0,

где гш 2 cos (г х) dx — импульс центробежных сил.

Так как гш = и, то

Интегралы уравнений (9-11) и (9-12) совпадают с уравнениями (9-8) и (9-9), если di = dpjp, что соответствует изоэнтропическому процессу.

Уравнения импульсов для абсолютного и относительного движений с учетом потерь можно получить, введя в (9-11) и (9-12) импульс сил трения; в этом случае i, с и w и являются параметрами действительного течения.

При исследовании ступени в рамках упрощенной одномерной схемы потока используется уравнение неразрывности:

m = Fpc = Fpw = Fqp а = F _п а а

где F_c — площадь сечения, нормального к вектору скорости с;

F_w — площадь сечения, нормального к вектору относительной скорости w; q_c и q_w — приведенные расходы при абсолютном и относительном движениях.

Из уравнения неразрывности находим:

где Р Р w y а с* a w — критические плотности и скорости

для абсолютного и относительного потоков.

Очевидно, статические параметры р, .р, Т как в абсолютном, так и в относительном движении одинаковы.

Действительный процесс движения газа в проточной части ступени отличается рядом особенностей, не учитываемых выведенными выше уравнениями. Так, поток газа в зазоре между направляющей и рабочей решетками обладает неравномерностью. В рабочих каналах, воспринимающих поток из зазора, течение газа оказывается периодически нестационарным, с непрерывной пульсацией скоростей и давлений.

Кроме того, поток совершает теплообмен с внешней средой в связи с непроизводительными потерями тепла и вследствие организуемого искусственного охлаждения лопаток, подверженные высоким нагрузкам. В уравнении энергии эта особенность может быть учтена введением соответствующего члена, учитывающего вмешний теплообмен.

При движении в .проточной части основной поток разветвляется; при этом некоторое количество газа, минуя рабочую решетку, протекает в зазоры между статором и ротором. В зависимости от распределения давлений в проточной части может происходить подсос газа через зазоры в основной тоток.

Таким образом, в общем случае поток газа в ступени подвергается различным внешним воздействиям, влияющим на процесс преобразования энергии. Оценка этих воздействий производится на основании данных эксперимента.

9-2. ПАРАМЕТРЫ ПОТОКА В АБСОЛЮТНОМ И ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ. ОДНОМЕРНАЯ СХЕМА

Величину постоянной в правых частях уравнений энергии (9-8) и (9-9)

С 2 . . W 2 — и 2 , . . /г> 1

можно определить из граничных условий.

При расчете ступени турбины обычно известны параметры течения на входе в рабочее колесо. Для входа имеем:

— С и U i + *1 = 2 + *1 = Const.

Обозначив, как и раньше,

где i_oc — энтальпия полного изоэнтропического торможения в произвольном сечении потока в абсолютном движении,

запишем (9-13) в такой форме:

или для совершенного газа:

^ де l ocv Тoci — энтальпия и температура изоэнтроЬичбсМб торможения на входе в рабочее колесо в абсолютном движении.

С другой стороны, при полном изоэнтропическом торможении потока в относительном движении его кинетическая энергия обратимо переходит в тепло. Энтальпия торможения определяется очевидным уравнением

Следовательно, уравнение энергии принимает вид:

где i — энтальпия полного торможения относительного

потока на входе в рабочее колесо.

Заметим, что если поток на входе не закручен и с_и]= = 0, то из (9-15) следует

Такой случай может иметь место только для чисто

реактивной ступени или для ступени центробежного компрессора.

С учетом выражений (9-14) и (9-16) уравнение (9-13) можно записать так:

Соответственно получаем зависимость между температурами торможения в абсолютном и относительном потоках:

_ С п а С„|М, ц2 и?

Уравнение (9-20) показывает, что температура торможения в обшем случае является переменной вдоль струйки величиной не только для абсолютного, но и для относительного движения. Представим (9-20) в несколько иной форме:

Tar + C t, U — C „ U

Разность температур торможения

Из уравнения (9-20a) следует, что температура торможения относительного потока меняется соответственно изменению окружной скорости вдоль трубки тока. При и = const температура Т_ош постоянна. На этом основании можно заключить, что температура торможения Т постоянна в ступени с осевым потоком газа. В радиальной ступени T_ow вдоль трубки тока меняется. Если в такой ступени поток направляется от оси вращения к периферии, то T_ow увеличивается. В случае, когда поток движется к оси вращения, Т убывает.

Полученный результат имеет простое физическое объяснение.

Полная энергия относительного потока, пропорциональная T_ow, изменяется вследствие работы центробежных сил, в поле которых движется газ. Если радиальные составляющие скорости не равны нулю (с_г—ш_гФ0) и струйка газа движется не только вдоль оси вращения, но и радиально, то центробежные силы совершают работу перемещения частиц в радиальном направлении и увеличивают или уменьшают полную энергию частицы в зависимости от направления потока. Если направление относительного потока совпадает с направлением центробежных сил (радиальная ступень с потоком газа к периферии), то Tow увеличивается. В-противном случае (радиальная ступень с потоком газа к оси вращения) полная энергия уменьшается.

Формула (9-206) показывает, что температура торможения в абсолютном движении во всех случаях убывает. Из рассмотрения принципа работы турбинной ступени следует, что в произвольном сечении трубки тока с_иы с_м!ы₁ и возрастает в направлении потока, так как работа к газу подводится.

Вернемся к уравнению энергии (9-13). Заметим, что величина постоянной в правой части уравнения (9-13) различна для разных струек, так как с_ихи_х может изменяться при переходе от одной струйки к другой. Отсюда заключаем, что, строго говоря, уравнение энергии следует применять для каждой струйки в отдельности. Для канала в целом уравнение (9-13) может бьпь использовано, если все величины, входящие в это уравнение, подсчитывать как средние по сечению канала.

Уравнению энергии в относительном движении можно придать известную форму, заменяя t по формуле

тогда согласно уравнению (9-16)

2 “TfeZiq — feZTi ’

где p_gw, p_o(B, a_ow—давление, плотность и скорость звука в изоэнтропически заторможенном относительном потоке.

Подчеркнем еще раз, что скорость звука и статические параметры течения р, р и Г для абсолютного и относительного движений имеют одну и ту же величину.

Скорость звука заторможенного относительного потока меняется вдоль струйки в соответствии с изменением энтальпии i_{ow a} OW a *W k—l k P° W _

l ow C p T OW ft—1 2 k—1 k—1 Рою

Аналогичные преобразования для потока в абсолютном движении приводят к соотношению

С помощью этих соотношений нетрудно получить выражение для характерных скоростей а,_с, с_макс, a._w и т. д. Так, например, для относительного потока находим:

Из уравнения (9-24) следует, что характеристики абсолютного потока, зависящие от величины полной энергии i_oc (от параметров торможения), меняются вдоль трубки тока. Следовательно, а,_с, с_макс и а являются переменными величинами для струйки газа в абсолютном движении.

В относительном движении критическая и максимальная скорости могут меняться или оставаться постоянными в зависимости от того, меняется ли или не меняется вдоль струйки окружная скорость и. Если вдоль струйки и = = const (ступень с осевым потоком), то i = const и соответственно a,_w = const и да_макс = const. При переменной вдоль струйки окружной скорости эти основные характеристики потока газа изменяются соответственно изменению и.

Уравнение (9-21) позволяет установить связь между температурами торможения в относительном и абсолютном потоках в следующей форме:

После замены (см., например, треугольники скоростей на рис. 9-2,6)

= 1 ““О — 1 ) = 1 ““О ~~sm 2 (g — а)~~ ‘ ( 9 ‘ 25a )

Уравнение (9-25а) показывает, что вдоль струйки отношение температур торможения меняется. При и = 0 и а=. = 2с„ отношение Т /7’„ = 1. Первый случай-соответ-

для абсолютного потока

Отсюда по известным формулам изоэнтропического процесса:

можно получить связи между -у и Л_ш, —— и и т. д.

С помощью уравнений (9-27) и (9-28) можно также получить зависимость между параметрами изоэнтропического торможения в абсолютном и относительном потоках:

С помощью уравнения (9-20) легко получить зависимость между параметрами полного торможения на входе и на выходе из колеса.

Для относительного потока получим [см. формулу (9-20а)]

Соответственно для абсолютного потока [см. формулу (9-206)]

с и u i с ы2 u 2

В формулы (9-27) — (9-39) входят безразмерные скорости абсолютного и относительного потоков. Связь между М_с и М_ш выражается так:

Последнее уравнение показывает, что отношение температур торможения T₀JT_0C служит переходным коэффициентом от абсолютного потока к относительному. Эта величина меняется вдоль струйки. На входе и на выходе т

из рабочего колеса для данного режима приобретает

Основные газодинамические зависимости, приведенные выше, справедливы как для аксиальной, так и для радиальной ступеней турбомашины.

Практические расчеты показывают, что влияние центробежного эффекта в осевой ступени невелико 116 . К этому выводу легко также прийти с помощью уравнения (9-33), из которого следует, что если отношение й_а/й_х мало отличается от единицы, то изменение температуры торможения относительного потока пренебрежимо мало. Только при значительном изменении окружной скорости вдоль трубки тока, как это, например, имеет место в ступени центробежного компрессора или радиальной турбины, влияние указанного эффекта будет существенным.

Для обычных турбинных радиальных ступеней отношение окружных скоростей uju_x колеблется в пределах

Рис. 9-7. Изменение температуры торможения относительного потока в зависимости от h₂/“i и М _w—

1,02—1,10. На основании рис. 9-7 заключаем, что для и₂[и 1 = 1,10 относительное изменение температуры торможения Т_ощ при м,_ш1 = 0,3 0,5 составляет 0,25 — 0,70%,

Изобразим изменение состояния газа вдоль струйки в тепловой диаграмме с учетом потерь энергии в элементах ступени турбины. Параметры полного торможения на входе в направляющую решетку находим в точке О (рис. 9-8): Рос и г осг Соответствующие статические параметры определены точкой 0[. Если обозначить статическое давление за направляющей решеткой р_х, то точка V фиксирует состояние газа при изоэнтропическом расширении, а точка 1 показывает действительное состояние потока (с учетом потерь). Потеря энергии выражается отрезком 1 — Г.

Давление торможения абсолютного потока за направляющей решеткой будет р_ш (энтальпия торможения остается

неизменной). Разность р_0с — Р_0с1 Эквивалентна потерям энергии Дh_c.

Коэффициент потерь в направляющей решетке равен:

где Я₀ — безразмерная скорость, эквивалентная изоэнтропи-ческому перепаду тепла в ступени Н₀.

Разность энтальпий торможения абсолютного и относительного потоков определяется по уравнению (9-19). Откладывая величину i_0cl — i_0wl от точки О’ на линии f_0c] = const, находим точку 2, которая определяет состояние заторможенного относительного потока на входе в рабочее колесо.

В рабочих каналах в результате потерь часть кинетической энергии необратимо переходит в тепло. В результате давление торможения в относительном движении падает. Если вдоль струйки газа окружная скорость не меняется, то соответствующий процесс изображается линией 2—3 (i₀ , = const). При увеличении и вдоль струйки (радиальный поток от оси вращения к периферии) i_Qw возрастает (пунктирная линия 2—3 ! ). Если и уменьшается, то i_0w снижается (линия 2— 1 Oail

Поток покидает ступень с некоторой абсолютной скоростью с₂. Часть кинетической энергии, эквивалентная скорости с₂, является потерей (Дh_a).

Коэффициент потерь с выходной скоростью

где р_т — давление тормол ения абсолютного потока за ступенью;

/?₀ — фиктивное давление торможения за ступенью (рис. 9-8).

Как видно из формул, коэффициенты потерь С₂ и С₃ зависят в неявной форме от — , так как от этой величи-

Рис. 9-8 Процесс в тепловой диаграмме для турбинной ступени 588

и Re на выходе из направляющей решетки.

йы зависят отношения температур -*— и -— . Величи-

также зависит от —; при изменении р- меняются числа М

на C_lt характеризующая потери в неподвил ной решетке,

В тепловой диаграмме отложим от точки 4′ вверх величину Дй_в; тогда получим точку 4, характеризующую состояние заторможенного абсолютного потока за ступенью-Предположим, что вся кинетическая энергия абсолютного потока за ступенью необратимо переходит в тепло; тогда на изобаре р_а в точке 5 определяется состояние газа за ступенью (процесс торможения за ступенью принят изобарическим).

Введем теперь понятие степени реакции. Степенью реакции называют отношение располагаемого теплового перепада на рабочей решетке к полному располагаемому перепаду тепла в ступени. Следовательно, степень реакции указывает ту часть располагаемой потенциальной энергии газа (тепла), которая Преобразуется в механическую работу непосредственно в рабочей решетке (на колесе).

По определению (рис. 9-8)

где /г₀₂ — изоэнтропический располагаемый перепад тепла

в рабочей решетке.

Формулу для степени реакции можно преобразовать к виду:

Отсюда следует, что для аксиальной ступени

степень реакции обращается в нуль при Я_в2 = Я_да1. Для радиальной ступени р = 0 при

Из этой формулы следует, что степень реакции MoJKet быть равна нулю при движении газа в радиальной ступени от оси вращения к периферии («₂ > при Я_а] >Я_щ2. При движении газа к оси вращения р = 0, если Я^ г 0с2 —

Отсюда с помощью уравнения (9-36) находим:

Тогда к. п. д. ступени на ободе можно найти по фор-

Из формулы видно, что даже в случае, когда потери энергии в направляющей и рабочей решетках отсутствуют (С₁ = С₂ = 0), к. п. д. ступени на ободе равен нулю при ‘Lcji — 0.

Формула (9-37) показывает, что такое условие выполняется, если

С и1 М 1 = С и2 и г-

Очевидно, что в этом случае поток газа в ступени работы не совершает. Величина Ъс_ии — 0 и для неподвижного колеса (и₁

Легко видеть, что в рассматриваемом случае с_и2и_г = 0, или с_и2 = 0 (и₂ ф 0).

По треугольникам скоростей можно заключить, что при этом выходные потери минимальны, так как при с_и2 — 0

9-3. УРАВНЕНИЯ ДЛЯ РАСЧЕТА РАСПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПОТОКА ПО РАДИУСУ В РАМКАХ СТРУЙНОЙ ТЕОРИИ •

Рассмотрим поток газа через ступень осевой турбомашины (рис. 9-9). Выберем три контрольных сечения: О—0 — перед направляющей решеткой, 1—1 — между направляющей и рабочей решетками и 2—2— за рабочей решеткой.

Рис. 9-9 Схема проточной части ступени с длинными лопатками.

Найдем распределение параметров таэтока по радиусу в двух контрольных сечениях (1—¦

1 и 2—2), если известны: распределение

параметров в сечении О—0, давление газа на корневом или среднем радиусе сечения 2—2, геометрические размеры ступени, число оборотов ротора турбины и аэродинамические характеристики решеток.

Имея в виду трудности, связанные с исследованием пространственного течения сжимаемой жидкости, можно в первом приближении рассмотреть упрощенную осесимметричную схему ,потока в ступени турбомашины.

Так, если принять, что течение в г ступени является установившемся и осесимметричным (д/дд=’0), а радиальные составляющие скорости (c_r = w ), а также их произ-‘дс, дс, dw, dw.

дг J весьма малы > то уравнения (1-17а) и (9-1) упрощаются и принимают вид (R=Q=z-

2 ui/r и получить из него первое уравнение (9-43).

Второе уравнение (9-43) выражает условие неизменяемости с_и по оси ступени. Из третьего уравнения нетрудно получить dc_a/dz = 0 три dp/dz=0, т. е. если давление по оси не меняется, то осевые составляющие скорости также сохраняются неизменными.

Принятым допущениям в наибольшей степени отвечает поток в контрольных сечениях 1—1 и 2—2 движение в межлопаточных каналах не подчиняется таким упрощенным закономерностям.

Введем дополнительно ряд упрощений. Пренебрегаем периодической нестационарностью потока, вызванной вращением рабочего колеса, или, точнее, считаем, что рассмотрение осредненных по времени скоростей также не вносит существенной ошибки. Предполагаем также, что после перестройки поток в контрольных сечениях движется по цилиндрическим поверхностям (т. е. радиусы кривизны меридионального сечения поверхности тока R на рис. 9-9 достаточно велики). Считаем, что внешний и внутренний теплообмен отсутствует, а решетки ступени обтекаются безотрывно.

Рассмотрим поток за направляющей решеткой. Воспользуемся упрощенным уравнением радиального равновесия (9-43), записав его в следующей форме: для сечения 0—0

где р₀, р₀, p_t, pj, с₀, я₀, с_и а_г — давления, плотности, скорости и углы потока перед и за направляющей решеткой.

Предполагаем, что функция ai = ai(r) известна. Вид этой функции определяется принятым законом закрутки направляющих лопаток. Очевидно, что поток газа должен удовлетворять уравнениям энергии и неразрывности. Для каждой элементарной кольцевой струйки, протекающей через направляющую решетку, уравнение энергии можно записать в такой форме:

/о’ = ‘t + 4 =^ f ‘ ¦ ( 9 — 45 )

где i’_Q — энтальпия торможения в зазоре;

c_lt, c_lt i_u, ii —скорости и энтальпии газа в конце изоэнтропического и действительного процессов расширения в направляющей решетке;

-ц₁ — к. п. д. направляющей решетки (приближенно определяемый как ij^cp 2 ).

Продифференцируем уравнение (9-45) по радиусу г:

Производная характеризует изменение энтальпии

потока в зазоре за направляющей решеткой по радиусу и, как известно, может быть записана таким образом:

Здесь p_u — плотность газа в конце изоэнтропического расширения в направляющей решетке; — плотность газа в конце действительного расширения (при наличии потерь).

где ^_lt = C_u/u _сХ—теоретическая безразмерная скорость за направляющей решеткой.

или с учетом (9-436) di

Подставляя (9-49) в уравнение энергии (9-46), получаем дифференциальное уравнение распределения абсолютных скоростей по радиусу в зазоре:

где h_ol = (? /2ij₁ — располагаемый теплоперепад в направляющей решетке в данном сечении по радиусу.

Интегрируя уравнение (9-50), находим:

где K_L — постоянная, отвечающая исходному (среднему или корневому) сечению.

Уравнение (9-51) в рамках рассматриваемой струйной задачи является наиболее общим.

Из (9-48) следует, Ч’го при дозвуковых скоростях и умеренных потерях в направляющей решетке отношение плотностей Рг1?_и близко к единице. Расчеты позволяю! — установить ту область значений Я_и и %, в которой можно принять = 1. Без большой погрешности такое упрощение допускается прй Я_и w 2 h + — = +

где о»! — относительная скорость на входе в рабочую решетку;

— энтальпия газа перед рабочей решеткой;

Tjg — к. п. д. рабочей решетки (т^^ф 2 ); ht — энтальпия газа за рабочей решеткой в изоэн-тропическом процессе.

Теоретическая и действительная скорости за решеткой связаны соотношением

Очевидно, что i_2t = i_2t (г) и ш₂ = ш₂ (г) являются искомыми функциями, а тг₁₃ = т)₂ (г) и w_l = w₁ (г) могут рассматриваться как заданные функции радиуса г.

Энтальпия потока за направляющей решеткой определяется по уравнению энергии:

После подстановки i₁ в (9-53) находим:

Продифференцировав уравнение энергии, получим (полагаем C ?

I w 2 uw 2 * u ‘l2 I ц I 1 1 __ Г1 /Q СЛД

dr I“ i)j dr ‘ 2tj₂ dr «I dr 2 J (9-54)

Заменим в уравнении (9-54)

Уравнения (9-54), (9-55) и (9-56) решаем совместно. После некоторых упрощений получаем искомое дифференциальное уравнение:

Уравнение (9-57) является нелинейным. Оно линеаризуется только в частном случае, когда d(c_alr)jdr = 0.

Интегрируя (9-57) в этом случае, т. е. с учетом d (c,i г)

где Кг — постоянная, определяемая для исходного (среднего или корневого) сечения.

Условие d(c_uir)/dr = 0 выполняется строго при закрутке ступени по методу постоянной циркуляции *. Однако, как показывает опыт, это условие приближенно осуществляется и в ряде других практически важных случаев.

Постоянные К и К₂ в уравнениях (9-51) и (9-58) определены, если известны скорости С] и w₂ в каком-либо сечении по высоте лопаток. Эта задача решается применением ур-авнения неразрывности для сечений 1-1

1 Поток газа в ступени за направляющей и рабочей решетками является закрученным, т. е. имеет неравномерное поле скоростей как при абсолютном, так и в относительном движении. Как показано в § 5-16, в таком потоке поле полной энергии будет неравномерным.

а 1в> а 1к — углы выхода потока у вершины и соответственно в корне воч сечении, r = rjr_k; r_k — радиус корневого сечения, г — радиус текущего сечения;

Подставив (9-61) в уравнение (9-50) и проинтегрировав последнее, получим:

Для определения скорости необходимо знать величину в корневом сечении. С этой целью преобразуем уравнение неразрывности (9-59), записав ‘его для сечений 0 — 0 и 1 — 1:

Pi c al r i d r ii

c al = c lA c l sina i = / ‘tft^^ sin a l> C 9 — 65 )

где dj принимается до формуле (9-61,.

Приведенные выше зависимости справедливы, если^поток в зазоре дозвуковой. При смешанных течениях в зазоре, когда в нижней

части ступени (у корневых сечений) Ci>e,i, формула (9-62) неприменима. В этом случае необходимо учитывать отклонение потока в косом срезе направляющей решетки.

Перейдем теперь к расчету потока за ступенью. Воспользуемся основным уравнением (9 57) и проинтегрируем его при т)₂= const и d (с_п1и) = 0 для принятого закона изменения углов по радиусу

Здесь b»₂fe — значение ш₂ в корневом сечении;

При известных значениях ш₂ легко определяется располагаемый теплоперепад в ступени.

С помощью выведенных уравнений можно рассчитать распределение параметров по радиусу в зазоре н за ступенью с лопатками постоянного профиля.

Располагаемый теплоперепад в направляющей решетке согласно (9 62) будет:

Найдем изменение степени реакции по радиусу:

Л 01 , Л 01к— , , Л 01к Нок

где р_к — степень реакции в корневом сечении.

Использовав (9-67), получим:

Отсюда можно получить приближенную формулу для определения реакции на среднем диаметре ступени с незакрученными лопатками, исходя из заданной величины р_к в исходном — корневом — сечении. Замечая, что г_т = 0/0 — 1 и полагая Ь₁ 5= 0, из формулы (9-68) получаем:

Формула (9-69) имеет ограниченную область применения Очевидно, что она справедлива для относительно больших 0, так как только в этом случае разность а, у вершины и у корня мала и можно принять b,^0.

Минимальную степень реакции в среднем сечении можно определить, полагая, что в корневом сечении 0. Тогда из (9-69)

или приближенно 5=0)

Изменение работы на венце по радиусу можно найти по формуле:

Функция с_я1 (г) также известна. Следовательно, величина L_u (г) определена.

Поле осевых составляющих скоростей за ступенью рассчитывается по формулам:

С а2 = С й2 tg “2 = ^„2 tg h = (°U2 + «) tg h

В заключение отметим, что исходная формула для степени реакции (9-68) позволяет определить разность р у вершины и у корня лопатки. Так как

то после подстановки в (9-68) получим:

где р_в — степень реакции у вершины.

Для прикидочных расчётов^можйо^рёйомендойать формулу 1 — р_в (в—1 2

Используя полученные соотношения, можно проанализировать изменения параметров ,по радиусу в зазоре и за ступенью и оценить дополнительные потери, возникающие в ступени с лопатками постоянного профиля.

Рис 9-10. Сравнение опытных и расчетных значенлй степени реакции в различных сечениях по радиусу ступени с лопатками постоянного профиля; в = 7,73; М₀ = 0,65.

Результаты соответствующих расчетов показывают, что дополнительные потери в ступени с незакрученными лопатками обусловливаются увеличением выходных потерь, изменением угла входа потока на рабочую ’решетку, а также изменением отдаваемой работы по радиусу. За ступенью поток вихревой; выравнивание поля скоростей сопровождается потерями кинетической энергии, которые должны быть включены в общий баланс потерь ступени.

Результаты расчетов по предлагаемой методике удовлетворительно совпадают с экспериментальными данными.

Подробное экспериментальное исследование потока в зазоре и за ступенью с цилиндрическими лопатками было выполнено в МЭИ при Q = d/l = 7,73. Был произведен расчет испытанных ступеней по приближенному методу, изложенному выше. Соответствующие кривые изменения реакции по радиусу приведены на рис. 9-10. Сравнение показывает удовлетворительную сходимость опытных и расчетных значений реакции. Опытные и расчетные значения углов, давлений и скоростей также удовлетворительно совпадают.

В заключение отметим, что при больших в изменение углов ai и Рг по радиусу невелико.

Расчет скоростей Ci и w₂ в таких ступенях можно производить по формулам, которые легко получить из основных уравнений (9-50) и (9-57) при следующих допущениях: г) 1 = const; т)2” const; ai = const и Рг = const.

9-5. НЕКОТОРЫЕ СПОСОБЫ ПРОФИЛИРОВАНИЯ ДЛИННЫХ ЛОПАТОК СТУПЕНЕЙ С ОСЕВЫМ ПОТОКОМ ГАЗА

Изложенная выше методика расчета ступеней с лопатками постоянного профиля позволяет оценить дополнительные потери в ступени, обусловленные изменением параметров и углов потока по радиусу в зазоре, а также возрастанием выходных потерь.

Результаты такого расчета приведены на рис. 9-11. Здесь даны кривые, устанавливающие дополнительные потери в ступени с лопатками постоянного профиля в зависимости от Q=d/l. Кроме того, на график нанесены опытные значения дополнительных потерь Ат]_м. При е 2 ^-^ = 0. (9-50а)

и согласно принятому допущению с_аХ = const, то уравнение (9-50а) преобразуется к виду:

Интегрируя это уравнение, получаем: c_alr = const.

Последнее условие выражает постоянство циркуляции скорости вокруг направляющей решетки. Действительно, в простейшем случае осевого входа в направляющую решетку (с ₀ = 0) циркуляция скорости равна:

с »о) = tc ,n —^Г с и — const —

где z — число лопаток в решетке.

Основоположником рассматриваемого метода является Н. Е Жуковский. Еще в 1912 г. при исследовании воздушных винтов Н. Е. Жуковский показал, что осевые скорости постоянны в радиальном направлении, если изменение окружных составляющих скоростей соответствует закону постоянства циркуляции. Хорошо известно, что воздушные бинты, а затем и вентиляторы, построенные согласно вихревой теории Н. Е. Жуковского, отличались высокой экономичностью. Для расчета длинных лопаток паровых и газовых тур’бин этот метод был впервые применен В. В. Уваровым.

С помощью уравнения (9-50а) нетрудно пайти распределение абсолютных скоростей в зазоре:

Изменение реакции по радиусу устанавливается с помощью очевидных соотношений

В соответствии с условием c_at г = const можно найти изменение углов абсолютной скорости по радиусу в таком виде:

Закрутку лопаток по условию постоянства циркуляции скорости можно осуществить с учетом потерь в решетках.

Для адиабатического течения (с учетом потерь) расчетные зависимости, полученные путем интегрирования исходных дифференциальных уравнений, даны в табл. 9-1.

Для течения с потерями, как это видно из формул, приведенных в табл. 9-1, условия c_ur = const и c_ai=eonst являются несовместимыми. При условии равномерного поля осевых скоростей в зазоре циркуляции скорости вокруг направляющей лопатки должны увеличиваться к ее вершине. Если в основу профилирования ступени положено условие постоянства циркуляции скорости, то осевые скорости в зазоре также несколько .увеличиваются к вершине.

Адиабатическое течение в зазоре при aj = const и rji = const подчиняется уравнению, получаемому инте-грированием (9-50), в следующем виде:

c al =c al/ c ulK cos 01,

1 — Tj! cos 2 X J[__

j/” 1 — r^cos^iK (1 — r 3 )

r 1 — cos 2 aj _K lr]2 + (1 —TjO r 2 ]

Следовательно, располагаемый теплоперепад в направляющей решетке будет:

— “о— 2l li cos2 a i

Отношение скоростей меняется по радиусу в соответствии с формулой

где x = u.Jc|_K — отношение скоростей для корневого сечения.

Угол относительного потока

Следует подчеркнуть, что осуществление метода закрутки при ai = const приводит к направляющим лопаткам переменного профиля по высоте, так как при малых 0 значительно меняются шаг лопаток и скорость с j вдоль радиуса. Следовательно, чтоб ы> осу щес т в ит ь условие ai=const, необходимо менять установочный угол профиля а_у, т. е. выполнять лопатку закрученной. При больших скоростях необходимо также учитывать влияние сжимаемости на средний угол за решеткой, что также приводит к необходимости закручивать направляющие лопатки.

Для большого числа ступеней представляется возможным направляющие лопатки выполнять без закрутки. Расчет направляющих решегок производится по формулам, приведенным в § 9-4. С помощью этих соотношений рассчитываются параметры потока в зазоре.

Расчет рабочих лопаток как при ai = const, так и при «1 —f( r ) производится, исходя из принятых условий за ступенью. Как указывалось, могут быть приняты условия отсутствия закрутки потока на выходе (с_и2 = 0), постоянства работы по радиусу (L_u = const) и др.

Расчет ступени при течении, близком к цилиндрическому, можно осуществить, разбив поток на ряд элементарных кольцевых струек. В пределах каждой струйки можно считать задачу одномерной и применять обычную методику расчета. Закрутка направляющей решетки, вообще говоря, может быть выбрана любой: ai = const; с_иГ=const; a=f(r). При этом, естественно, для определения параметров в зазоре можно воспользоваться одним из частных решений (9-50). Определив параметры в зазоре, записываем уравнения неразрывности для каждой струйки в контрольных сечениях 1—1 и 2—2:

где AG — расход пара через элементарную струйку;

и Ргt — плотности в конце изоэнтропического расширения в направляющей и рабочей решетках;

c_u, w_2t — теоретические скорости выхода потока; ft и /₂ — площади выходных сечений в пределах одной элементарной струйки; jj-i, ja₂ — коэффициенты расхода в данном кольцевом сечении направляющей и рабочей решеток.

Из уравнения неразрывности и треугольников скоростей определяем параметры, необходимые для проектирования рабочей решетки. Полный расход газа через ступень О равен сумме расходов по всем элементарным струйкам. Общий к. п. д. ступени находится по к. п. д. элементарных струек как усредненный по расходу.

При подобном методе расчета коэффициенты расхода щ и fi_g и коэффициенты скорости следует принимать переменными, зависящими от геометрических и режимных параметров в рассматриваемых сечениях решеток. Описанный метод расчета весьма прост и дает надежные результаты.

Построение направляющей и рабочей лопаток осуществляется по данным расчета закрутки. По вычисленным значениям М_е1 (г) и а, (г) подбираются профили в корневых, средних и верхних сечениях направляющей решетки. При больших теплоперепадах в ступени в корневых сечениях >1, а в периферийных М^, f /

о.г о.« o,s о,8 р Рис. 9-12. Сопоставление некоторых методов закрутки лопаток.

сти углов входа потока Pi в верхнем и корневом сечениях, к снижению лотерь от утечек, уменьшению осе-зых усилий и т. п. Для компрессорной ступени с реакцией р=0,5 за счет выравнивания поля скоростей по высоте может быть отодвинута предельная граница по числу М, повышены окружные скорости и, следовательно, увеличен коэффициент напора при сохранении высокой экономичности ступени.

Рис. 9-13 Схема кольцевой решетки направляющих профилей с наклонными кромками и меридиональным профилированием.

Для ступеней турбин с небольшими высотами лопаток (Т С 1

Как указывалось (§ 8-8), применение меридионального профилирования в ступенях с небольшими высо-

Рис. 9-14. Зависимость к. п. д. к)_ог и реакции от и/с₀ для ступени с меридиональным профилированием (КД-2-2Ам) и ступени с цилиндрическими обводами (КД-2-2А); 8 = 16; = 0,5.

тами лопаток позволяет не только уменьшить разность [реакций, ,но и значительно уменьшить потери ® ‘Направляющих решетках. На рис. 9-14 представлены резуль-гаты испытаний двух ступеней (ii»0,5; 0=16) с криволинейным и цилиндрическим обводами верхнего бандажа. Видно, что ступень с мериодинальным профилированием имеет более высокий к. П. д. (на 1,5—2%), а разность реакций Др — р_в — р_к уменьшается более чем в 3 раза (с 16 до 5%).

Для ступеней с 0 г L F

(где F_r—радиальная составляющая силы воздействия лопаток на поток) видно, что при 7v у>+20°. Графики изменения потерь по высоте решеток (рис. 9-16) показывают, что для отрицательных углов наклона потери возрастают в корневых сечениях, где возникает отрыв потока. Для решеток с наклоном лопаток по потоку, когда осуществляется поджатие потока в корневых сечениях, .потери увеличиваются в периферийных сечениях.

Опыты показали, что одновременным введением меридионального профилирования верхнего обвода решетки и наклоном лопаток можно уменьшить потери в верхних сечениях (у>0). При этом оба фактора — наклон лопаток по потоку и профилирование верхнего

1 Исследование ступеней с наклонными лопатками проведены Ю. И. Митюшкиным (ЛМЗ) и Г. А. Филипповым (МЭИ).

обвода — позволяют более резко снйзить разность реакций Др — р_в р_к.

Приближенная формула для определения реакции в ступени с различными углами наклона лопаток у может быть получена путем совместного решения уравне-

Рис. 9-16. Характер изменения потерь по высоте решетки при различных углах наклона лопаток (в = 8,5; /, = 1,0; а, = 15°).

ний количества движения и радиального равновесия цилиндрического потока (9-73). Сила воздействия лопаток на поток определяется через окружную составляющую по уравнению (с_г«0):

где Р_п — окружная составляющая силы воздействия лопаток на поток.

ГТринйв линейный з&кон изменения t_u ho Ширийё решетки для средней линии канала с_а = хс_я1/В, получим:

Подставляя F_r в уравнение (9-73), находим:

dp Cj cos c?j C| sin a, cos a,

Из последнего уравнения совместно с уравнением энергии получим:

/Is-т dr — cos 2 a. — .

Проинтегрировав это уравнение для случая a_t = const получим распределение скоростей по высоте лопаток:

i Г sin dj cos a, (r,— r_R) eX ^ I о tg (90 — y)

Реакция в произвольном сечении зазора рассчитывается по формуле

2sin a, cos (r, — r )

Разность реакций при p_A = 0 и 6^1,5В (b — хорда профиля)

Полученные формулы дают несколько завышенные значения разности реакций, что связано в основном с отклонением потока в зазоре ступени от коаксиального, наличием радиальных перетеканий газа в пограничном слое лопаток, утечками в ступени, влиянием рабочего колеса. Погрешность расчета объясняется также принятым приближенным законом изменения с_и по оси канала и пр.

Влияние перечисленных факторов учитывается по -опытным данным введением коэффициента Л = 0,65 в формулу (9-76).

Расчет реакции в ступени с наклоном лопаток по потоку и меридиональным профилированием зерхнего обвода осуществляется по формуле

полученной с учетом влияния кривизны верхнего обвода на распределение скоростей по радиусу в зазоре.

Опыт подтверждает’ удовлетворительную точность формулы (9-77) при 0 > 6.

Для ступеней с малыми в е /„, угол входа потока уменьшился со 155° до 127°. Число М_с1 возросло у вершины лопатки до 0,9, а число М^_г уменьшилось до М_да2=1_>08.

Последние ступени турбин часто приходится выполнять с коническими обводами (рис. 9-12). Наличие конусности приводит к уменьшению реакции в ступени.

Рис. 9-17. Изменение параметров по высоте лопатки (0 = 2,6; е₂ = 0,27).

——с наклоном кромок, -—кромки радиальные.

Для конусной направляющей решетки изменение реакции по радиусу можно приближенно определить по формуле

где /C,=l-<-siii 2 a,tg 2 8_B — коэффициент, учитывающий влияние конусности; 8_в — угол конусности у вершины.

ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ГАЗОВЫХ ПОТОКОВ И ПРОТОЧНОЙ ЧАСТИ ТУРБОМАШИН

10-1. ЭКСПЕРИМЕНТАЛЬНЫЕ СТЕНДЫ ДЛЯ ИССЛЕДОВАНИЯ ПРОТОЧНЫХ ЧАСТЕЙ ТУРБОМАЩИН

Задачи опытного исследования проточной части турбомашин можно разбить на тр’и группы В первую грулпу включаются вопросы, связанные с исследованием структуры потока в отдельных, рассматриваемых изолированно элементах ступени и в первую очередь в направляющей и рабочей решетках

Вторая группа задач заключается в дифференцированном изучении физических явлений, происходящих в ступени

Третья группа задач сводится к определению опытных коэффициентов, необходимых для теплового расчета турбомашины, и к выяснению зависимости этих коэффициентов от основных конструктивных, геометрических и режимных параметров ступени

Основные требования к эксперименту в лабораторных условиях формулируются теорией подобия Практически не все эти требования могут быть реализованы с одинаковой степенью точности, так как действительные процессы в турбомашине отличаются большой сложностью Поэтому при постановке эксперимента в каждом отдельном случае следует установить наиболге существенные особенности процесса, пренебрегая его второстепенными признаками Правильное решение этого вопроса определяет направление и методику экопримента, а также теоретическую и практическую ценность результатов исследования Если основной целью эиспер лмента является получение интегральных характеристик ступени, то очевидно, что в модельных условиях должны быть воспроизведены все наиболее существенные признаки процесса Поэтому опытное исследование характеристик ступени необходимо проводить на специальных экспериментальной турбине или экспериментальном компрессоре, позволяющих установить надежные значения характеристик и изучить основные особенности потока в решетках

Последняя задача, однако, решается в экспериментальной ча^-шине нелегко, так как требует применения сложной специальней измерительной аппаратуры. Поэтому при детальном изучении обтекания решеток, при изучении механизма образовании и развития потерь в изолированно рассматриваемых решетках необходимо прибегать и к другим, более простым методам эксперимента, поступаясь некоторыми требованиями теории подобия Отсюда следует, что наряду с использованием экспериментальной турбомашичы в качестве основного метода исследования необходимо применять и более простые и поэтому широко распространенные методы испытания неподвижных решеток

Исследования элементов проточной части паровых и газовых турбин могут производиться на водяном паре или на воздухе, при-

Чем схема йсйктателыШй Менда сущ&стйемно За1й?йт От Приме няемого рабочего тела Исследования элементов ком пресс о,р а производятся, естественно, на воздухе

Рис 10-1 Принципиальная схема воздушного экспериментального стенда 1 — двигатель; 2—компрессор, 3— ресивер, 4—фильтр; 5 — подогреватель; 6 и 7 —статические установки, 8, ^—экспериментальная турбина 10 — установка для взвешивания реактивных усилий, 11 — аэродинамическая труба, 12 — оптическая установка, 13—холодильник, / 100° С значительно проще, че>м «а паре при температурах 250—350° С Это определило широкое применение воздуха в лабораторных исследованиях проточных частей цурбомашин

Однако ряд задач, связанных с длительной работой эксперимента тыкых установок с большими секундными расходами и при больших скоростях, требует чрезвычайно мощных и громоздких компрессорных установок Работы, связанные с исследованием последних ступеней конденсационных паровых турбин, могут проводиться на воздухе только частично, а ряд вопросов вообще не может быть решен на воздушном стенде

Оптимальным решением, дающим наибольшею возможность ведения различных исследований проточных частей турбин с минимальной затратой времени и средств, является использование ком бинированного паровоздушного стенда, принципиальная схема которого приведена на рис 10-2

Большинство установок такого стенда может работать как на паре, так и на воздухе, что позвочяет выбирать оптимальный для данного эксперимента вид рабочего тела Воздушный контур стемда-не отличается от приведенного на рис 10-1 Использование пара позволяет легко получать большие секундные расходы, большие скорости, независимо менять числа М и Re, обеапечивает проведение всех исследований, связанных с влажностью Пар через редукционно-охладительную установку 29 подается к экспериментальным установкам стенда, проходит через них и направляется в основной конденсатор 21 Конденсат конденсатным насосом 24 подается в мерный бак 25, а затем в линию возврата конденсата ТЭЦ

Паровоздушный стенд состоит из установки для исследования кольцевых неподвижных решеток 7, высокооборотной одноступенчатой экспериментальной осевой турбины 8, двухвальной экспериментальной турбины 14, предназначенной в основном для исследования последних ступеней, экспериментальной турбины для исследования радиально осевых ступеней 20, осевого 26 и центробежного 27 экспериментальных компрессоров с паротурбинным приводом 28 и установки для испытания плоских решеток 6

При необходимости в паровоздушном стенде могут быть использованы эжекторные аэродинамические трубы 18 и 19, воздушный поток в которых создается паровым эжектором, засасывающим воздух из атмосферы

В схему стенда включен блок 17, позволяющий устанавливать для периодических испытаний различные вспомогательные детали турбин

Для отсоса пара из уплотнений экспериментальных турбин используется вспомогательный конденсатор 23 Вакуум в конденсаторах поддерживается паровыми эжекторами 22

Выхлопные патрубки турбин жепательчо снабжать дроссельными устройствами, позволяющими поднимать противодавление за рабочим колесом до 3—5 ата Для подавляющего большинства экспериментов достаточно давление свежего пара 5—7 ата при температуре 250—350° С

Редукционно-охладительная установка должна допускать питание стендов не только перегретым паром пониженных параметров, но и влажным паром