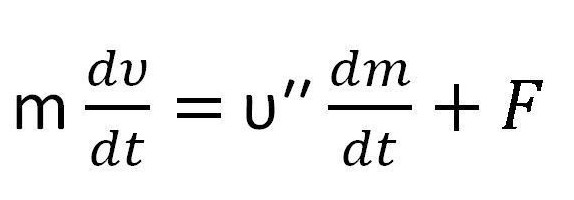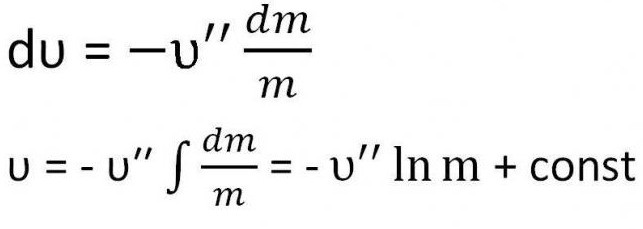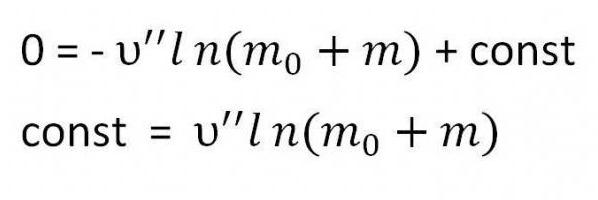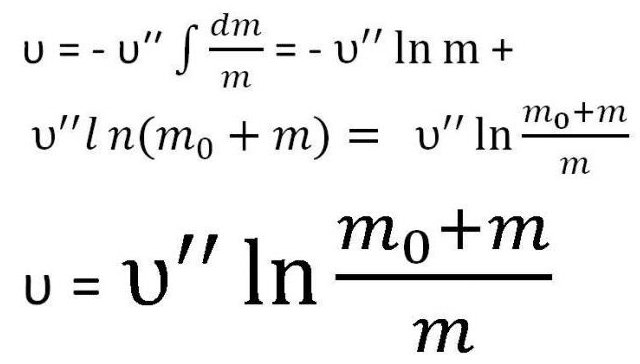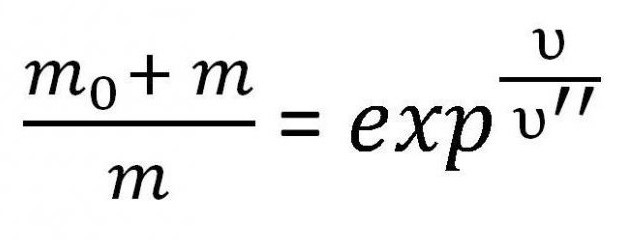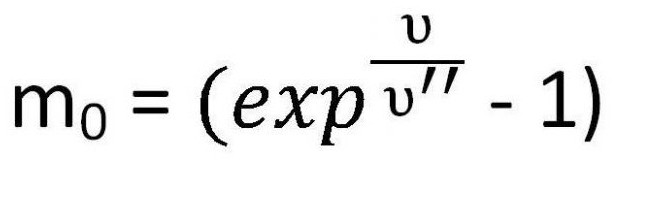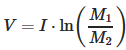Основное уравнение движения ракеты циолковского

Видео:Уравнение Мещерского, формула ЦиолковскогоСкачать

Формула Циолковского: использование и пример

Формула Константина Эдуардовича Циолковского выражает максимальную скорость летательного аппарата, которой он достигает во время полета при реактивном движении. Она получается при интегрировании уравнения Мещерского.

Видео:Формула ЦиолковскогоСкачать

Формула Циолковского

Эта формула выражает скорость ракеты, переданную газами от сожженного топлива. Уравнение Мещерского и формула Циолковского неразрывно связаны — уравнение Мещерского описывает массу материальной точки, которая изменяется со временем, в то время как при реактивном движении ракеты постоянно идет уменьшение ее массы из-за сгорания топлива. Изменение скорости при изменяющейся массе (уменьшающейся в нашем случае) движущегося тела — вот что подразумевает под собой реактивное движение. Формула Циолковского основывается именно на нем.

Для решения ряда задач теоретической механики в области реактивного движения используют уравнение Мещерского (основное уравнение материальной точки переменной массы) и формулу Циолковского (формула конечной скорости летательного аппарата), которые называются основными соотношениям теории реактивного движения.

Основой при проектировании и планировании в области космических полетов является именно формула Циолковского, вывод которой стал настоящим прорывом для освоения космоса.

Видео:Формула ЦиолковскогоСкачать

Задачи Циолковского

Для того, чтобы разрешить проблему межпланетных перелетов, К. Э. Циолковский рассмотрел в качестве средства перелета ракету. Он вывел формулу, с помощью которой можно получить зависимость массы летательного аппарата с топливом и скорости отдаления продуктов сгорания используемого топлива ракеты относительно нее. Покажем две его задачи:

• Исследование движения тела с переменной массы с действующей на него одной реактивной силы.
• Исследование движение тела в однородном поле силы тяжести переменной массы вблизи поверхности Земли.

Видео:Главная формула космонавтики. Формула Циолковского | Море ЯсностиСкачать

Предисловие

Для всех космических полетов изначальной и основополагающей стала формула Циолковского для скорости ракеты, вывод которой представлен ниже.

Для начала необходимо приняв ее, грубо говоря, за материальную точку. На нее будут действовать силы притяжения Земли и других небесных тел (в момент взлета сила гравитации Земли будет, конечно же, наиболее сильной), сила сопротивления воздуха с одной стороны и противоположно им направленная реактивная сила, возникающая из-за выброса сгоревшего газа у основания тела. Ракета с большой силой выбрасывает эти газы, которые сообщают ей ускорение, направленное противоположно стороне выброса. Теперь необходимо представить эти рассуждения в виде формулы.

Сам принцип полета ракеты достаточно простой. С большой скоростью из ракеты вырывается газ, полученный при сгорании топлива, который сообщает самой ракете определенную силу, которая действует противоположно направлению движения. Так как считается, что внешние силы не действуют на ракету, то система будет замкнутой, и импульс ее не зависит от времени.

Видео:Дифференциальные уравнения 3. Формула ЦиолковскогоСкачать

Уравнение Мещерского

Одним из основных примеров движения тела с изменяющейся массой является ракета с одной ступень, масса которой изменяется только из-за сжигания топлива, содержащегося в ней. Масса такой ракеты складывается из неизменяющейся (сама ракета и ее полезная нагрузка) и изменяющейся (топливо). Такой пример является упрощенной моделью.

Однако в современном ракетостроении используются многоступенчатые ракеты. Принцип их работы заключается в том, что благодаря большому объему ступеней они способны перевозить и использовать после взлета гораздо большее количество топлива. После его сгорания, ракете сообщается значительный импульс (гораздо больший, чем тот, которого можно добиться, используя одну ступень), а ставшие ненужными части открепляются от основы, уменьшая общий вес на 80-90%. Тем не менее, для расчета параметров многоступенчатой ракеты необходимо сложить показатели каждой из ее составляющей.

Дифференциальное уравнение Мещерского описывает движение материальной точки с переменной массой.

(m+dm)(υ+dυ) + dm′ υ′ — mυ = Fdt — в момент времени dt (разность между силой в момент времени t и dt+t и будет приращением).

Где m и υ зависят от времени, dt — какое-то время полета. За его образуется сила перемещения газа — dm′ υ′, dm′ — масса образованного из топлива газа. F — равнодействующая сила.

В описанном выше выражении приращения массы ракеты и газа и скорости устремляется к нулю, поэтому выражение принимает следующий вид:

причем υ′′ равняется разности скорости газа и скорости и является скоростью истечения газа.

Оно и называется уравнением Мещерского.

Видео:Урок 106. Реактивное движениеСкачать

Вывод формулы Циолковского

Необходимо вывести формулу, описывающую движение тела с переменной массой. Формула Циолковского таковой и является. Вывод представлен ниже.

В данных вычислениях считается, что на движущееся тело не действуют внешние силы, то есть F = 0.

Так как воздействие внешних сил на летящую ракету равно нулю, то она движется прямолинейно, а скорость движения противоположно направлена скорости выхода газа. Соответственно, υ = -υ′′

Получается выражение, которое необходимо проинтегрировать.

Необходимо найти константу. Для этого достаточно подставить в уравнение начальные условия — скорость равна нулю, а масса — сумме массы топлива и массы ракеты (m₀ + m)

Вообще говоря, m в формуле складывается из двух параметров — из полезной нагрузки и конструкции ракеты. Полезной нагрузкой называется общая масса груза и экипажа.

Подставляем найденную константу в формулу. В результате и получается выражение искомой формулы.

Это и есть один из вариантов формулы Циолковского для скорости. Однако иногда необходимо принять во внимание именно массу. Поэтому ее иногда записывают следующим образом:

Данная формула используется для расчета массы топлива, которая требуется для развития определенной скорости при заданных условиях.

Рассмотрю далее небольшую задачу. Предположим, ракете необходимо развить первую космическую скорость для вращения по орбите Земли. Тогда для этого необходимо в первую очередь рассчитать массу топлива, конечно же. Тогда ее очень просто выразить из формулы Циолковского.

Видео:Формула ЦиолковскогоСкачать

Релятивистская механика

Все вышеописанные формулы могут применяться только в том случае, когда скорость ракеты много меньше скорости света (υ

Видео:ОСНОВЫ РАКЕТОСТРОЕНИЯ. ФОРМУЛА ЦИОЛКОВСКОГО, УДЕЛЬНЫЙ ИМПУЛЬС, ХАРАКТЕРИСТИЧЕСКАЯ СКОРОСТЬ.Скачать

Жестокость формулы Циолковского

Жестокими законы окружающей нас природы можно назвать только в переносном смысле. Мы создали машины, способные освободить нас от уз, удерживающих в гравитационном колодце всё человечество, но управление некоторыми из их аспектов остаётся вне наших сил. Если мы хотим начать наше путешествие по Солнечной системе, то эти ограничения придётся как-то обходить.

Современные ракеты отбрасывают часть собственной массы в виде газа из сопел двигателей, что даёт им возможность двигаться в противоположном направлении. Это реально благодаря третьему закону Ньютона, который был сформулирован в 1687 году. Всему нашему ракетному движению мы обязаны формуле Циолковского 1903 года.

В формуле всего четыре переменных (слева направо): конечная скорость летательного аппарата, удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива), начальная масса летательного аппарата (полезная нагрузка, конструкция и топливо) и его конечная масса (полезная нагрузка и конструкция).

Как можно изменить одну из переменных, если три другие уже заданы? Это просто невозможно, никакая форма желания, хотения или просьб здесь не поможет.

Именно потери на гравитацию определяют пределы человеческого исследования космоса, и мы вынуждены их учитывать, когда мы выбираем место, куда мы хотим отправиться. Сегодня таких мест не так уж и много. С земной поверхности мы можем оказаться на орбите Земли, с орбиты Земли можно отправиться на поверхность Луны, или на поверхность Марса, или в пространство между Луной и Землёй. Возможны различные комбинации, но с текущим развитием технологий это самые вероятные точки назначения.

Представленные ниже значения не учитывают никакие потери на, к примеру, сопротивление атмосферы, но значения достаточно близки для иллюстрации того, что нужно принять как должное. Это в некотором роде стоимость полёта.

Как можно заметить, путь от Земли на орбиту, эти жалкие 400 километров — это самая затратная часть полёта. Это целая половина «стоимости» полёта на Марс, даже до Луны добраться «стоит» меньше. Всё это связано с гравитационным притяжением нашего космического дома.

А лететь нам придётся на ракете с химическими двигателями; пусть и есть перспективные разработки, но реальными остаются традиционные, используемые уже на протяжении более 60 лет в пилотируемой космонавтике двигатели. Химическое топливо накладывает ограничение на количество энергии, которое можно из них извлечь, а значит и вложить в ракету, и мы используем самые эффективные реакции, известные человечеству. И вновь нам придётся смириться с некоторым значением переменной, которое мы не в силах изменить.

Ниже представлены как некоторые виды ракетного топлива, которые хоть раз были использованы для приведения в движение аппаратов с человеком на борту или планируются к использованию, так и их удельные импульсы. Метан-кислород находится под рассмотрением для будущих экспедиций на Луну и Марс. Самовоспламеняющееся двухкомпонентное жидкое ракетное топливо использовалось для посадочного лунного модуля программы «Аполлон» из-за своей простоты.

Самой эффективной парой остаётся кислород-водородная, и химия не может дать нам больше. В конце 70-х годов прошлого века ядерный ракетный двигатель с водородом в качестве рабочего тела, который разгоняла теплота управляемой ядерной реакции, выдал 8,3 км/с.

Итак, единственное, что мы теперь можем изменить в формуле Циолковского — это отношение масс летательного аппарата. Ракета должна быть построена таким образом, чтобы это отношение имело какое-то заданное значение, иначе она просто не достигнет своей цели. Что-то можно сделать, если добавить несколько гениальных решений в конструкцию, но в целом это мало повлияет на результат — химию топлива и гравитацию небесных тел не изменить.

Итак, что имеем? Вот процентное соотношение топлива от общей массы ракеты, необходимое для попадания ракеты на орбиту Земли.

Полученные цифры не учитывают разнообразные потери сопротивления атмосферы, неполного сгорания и других отрицательных факторов, поэтому реальное отношение чуть ближе к 100%. Прекрасные инженерные решения типа разделения на ступени, нескольких видов топлива (например, керосин или твёрдое топливо для первой ступени, водород для остальных) очень помогают в ситуации, когда лишь порядка 10% от массы аппарата остаётся на собственно ракету. Масса полезной нагрузки иногда и в буквальном смысле идёт на вес золота.

Характеристики реальных ракет не сильно отличаются от этих идеальных, полученных без учёта множества факторов значений. Самая большая в истории человечества ракета «Сатурн-5» на стартовом столе имела топлива 85% от всей своей массы. У неё было три ступени: первая работала на керосине и кислороде, вторая и третья — на водороде и кислороде. Такой же показатель у «Шаттлов». «Союз» использует керосин на всех своих ступенях, поэтому масса его топлива составляет 91% от общей массы ракеты. Использование пары водород-кислород сопряжено с большим количеством технических трудностей, но эта комбинация более эффективна; керосин в паре с кислородом предоставляет возможность использовать более простые и надёжные решения.

15% массы ракеты — это куда меньше, чем кажется. У ракеты должны быть баки, трубы, ведущие к двигателям, корпус, который должен быть в состоянии выдерживать как сверхзвуковой полёт в атмосфере после нечеловеческого жара стартовой площадки, так и холод безвоздушного пространства. Ракету нужно вести, управлять ей с помощью сверхзвуковых рулей и маневровых двигателей. Хрупкие тела людей в космическом корабле нужно обеспечивать кислородом, а также удалять углекислоту, их нужно защитить от жара и холода, дать им возможность безопасно вернуться на поверхность родной планеты. Наконец, люди — не единственная нагрузка ракеты: мы не запускаем людей просто для развлечения, вернее, мы можем запустить человека ради самого факта, но лишь один раз. С людьми в космос летит и разнообразное оборудование для проведения экспериментов, поскольку полёты в космос имеют целью научные исследования.

Реальная масса полезной нагрузки ракет куда меньше этих 10%—15%. «Сатурн-5», единственная ракета, которая помогла человеку ступить на Луну, доставляла на орбиту Земли всего 4% от своей общей массы, всего же на орбиту доставлялось 120 тонн. «Шаттлы» могли доставлять примерно столько же (100 тонн), но реальная полезная нагрузка составляла порядка 20 тонн, 1% от общей массы.

Сравним ракеты с привычными нам транспортными средствами. (Конечно, ракета имеет баки с окислителями, а земной транспорт использует для этого кислород воздуха.)

Легко заметить, как отличаются материалы и конструкция транспортного средства в зависимости от относительной массы топлива. Транспорт с топливом массой менее 10% от его общей массы обычно делается из стали, а над его конструкцией нет нужды особо думать: прикрепи эту часть к той и усиль корпус, где требует интуиция. Десятитонный грузовик можно сильно перегрузить, но он будет продолжать двигаться, пусть и медленно.

Воздушный транспорт требует уже более серьёзного подхода и лёгких конструкций из алюминия, магния, титана, композитных материалов. Тут уже просто так ничего не поменяешь, а над любой мелкой деталью нужно подумать дважды. Машины подобного рода не могут работать так далеко за пределами своих лимитов нагрузок. 60%—70% от массы этих аппаратов составляет собственно вес транспортного средства с полезной нагрузкой, и с применением некоторых инженерных решений возможна комфортная, безопасная и выгодная эксплуатация.

А ракеты, где 85% приходится на топливо, находятся на пределе наших инженерных способностей. Мы едва можем их производить, они требуют постоянного улучшения для возможности их использовать. Внешне небольшие изменения требуют огромного количества разнообразного анализа и тестирования прототипов в аэродинамических трубах, вибростендах, а для пробного запуска следует удалить персонал в бункер на пару—тройку километров от стартовой площадки — даже после всех этих проверок возможны происшествия. Очень часто превышать нагрузки более, чем на 10% от заданного техническими требованиями, нельзя. Это аналогично ситуации, когда после разгона до 44 километров в час велосипед развалится на мельчайшие винтики просто потому, что предельной скоростью является 40 км/ч.

Чудо массового производства, пивная алюминиевая банка примерно на 94% состоит из своего содержимого, и лишь 6% приходится на корпус, но каким-то образом этот показатель лучше у внешнего бака Шаттла, несмотря на то, что в нём содержится не напиток чуть холоднее комнатной температуры, а высокоактивные жидкости температурой примерно на 20 градусов выше температуры абсолютного нуля, сжатые до ужасного давления. При этом этот топливный бак может выдержать перегрузку в 3 g, сохраняя поток окислителя и горючего на уровне 1,5 тонн в секунду.

Дон Петтит описывает детали экспедиции STS-126 ноября 2008 года. Двигатели челнока должны были отключиться при достижении скорости 7824 м/с, но если бы это произошло на уровне 7806 м/с, то космический аппарат стал бы спутником Земли, но не попал бы на целевую орбиту. Говоря проще, «Индевор» не достиг бы МКС. Большая ли это разница? Это примерно аналогично ситуации, когда нужно заплатить 10 долларов, и для этого не хватает всего лишь двух центов (0,2%). Хорошо, в этом случае можно было бы использовать часть топлива для орбитальных манёвров. Если бы скорость была всего на 3% ниже, то не хватило бы и этих запасов, и челнок пришлось бы сажать где-то в Испании. Эти 3% можно было потерять, если маршевый двигатель отключился бы всего на 8 секунд раньше.

Представим наилучшее стечение обстоятельств: бак для Шаттла (массу двигателей мы отбросим) и водород-кислородное топливо. Если подставить значения в формулу Циолковского, то станет ясным, что при радиусе нашей планеты в полтора раза больше его нынешнего мы никогда бы не достигли космоса только за счёт технологии химических ракетных двигателей.

И всё это — последствия формулы Циолковского. Если мы хотим избавиться от её жестокого господства, нам придётся создать работающие версии принципиально новых двигателей. Возможно, тогда ракеты станут такими же безопасными, привычными и надёжными, как и реактивные пассажирские самолёты.

Видео:KSP Гайд - Формула Циолковского, или сколько нужно топлива?Скачать

Формула Циолкоцфвского

Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

,

V — конечная (после выработки всего топлива) скорость летательного аппарата; I — удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива); M1 — начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо). M2 — конечная масса летательного аппарата (полезная нагрузка + конструкция);

Эта формула была выведена К. Э. Циолковским в рукописи «Ракета» 10 мая 1897 года.

Однако первыми уравнение движения тела с переменной массой решили английские исследователи У. Мур, а также П. Г. Тэйт и У. Дж. Стил из Кембриджского университета соответственно в 1810—1811 гг. и в 1856 году.

Формула Циолковского может быть получена путём интегрирования дифференциального уравнения Мещерского для материальной точки переменной массы:

, в котором m — масса точки; V — скорость точки; u — относительная скорость, с которой движется отделяющаяся от точки часть её массы. Для ракетного двигателя эта величина и составляет его удельный импульс I

Для многоступенчатой ракеты конечная скорость рассчитывается как сумма скоростей, полученных по формуле Циолковского отдельно для каждой ступени, причем при расчёте характеристической скорости каждой ступени к её начальной и конечной массе добавляется суммарная начальная масса всех последующих ступеней.

M1i — масса заправленной i -ой ступени ракеты; M2i — масса i -ой ступени без топлива; Ii — удельный импульс двигателя i -ой ступени; M0 — масса полезной нагрузки; N — число ступеней ракеты.

Тогда формула Циолковского для многоступенчатой ракеты может быть записана в следующем виде:

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Отличие реальной скорости ракеты от характеристической

Поскольку в условиях реального полёта на ракету кроме тяги двигателей действуют и другие силы, скорость, развиваемая ракетами в этих условиях, как правило, ниже характеристической из-за потерь, вызываемых силами гравитации, сопротивления среды и др.

В таблице 1 приведён баланс скоростей ракеты Сатурн V при выводе корабля Аполлон на траекторию полёта к Луне.

Как видно из таблицы 1, гравитационная составляющая является наибольшей в общей величине потерь. Гравитационные потери возникают из-за того, что ракета, стартуя вертикально, не только разгоняется, но и набирает высоту, преодолевая тяготение Земли, и на это также расходуется топливо. Величина этих потерь вычисляется по формуле:

,

где g(t) и γ(t) — местное ускорение гравитации и угол между вектором силы тяги двигателя и местным вектором гравитации, соответственно, являющиеся функциями времени по программе полёта. Как видно из таблицы 1, наибольшая часть этих потерь приходится на участок полёта первой ступени. Это объясняется тем, что на этом участке траектория отклоняется от вертикали в меньшей степени, чем на участках последующих ступеней, и значение близко к максимальному значению — 1.

Аэродинамические потери вызваны сопротивлением воздушной среды при движении ракеты в ней и рассчитываются по формуле:

,

где A(t) — сила лобового аэродинамического сопротивления, а m(t) — текущая масса ракеты. Основные потери от сопротивления воздуха также приходятся на участок работы 1-й ступени ракеты Сатурн V, так как этот участок проходит в нижних, наиболее плотных слоях атмосферы.

Корабль должен быть выведен на орбиту со строго определёнными параметрами, для этого система управления на активном участке полёта разворачивает ракету по определённой программе, при этом направление тяги двигателя отклоняется от текущего направления движения ракеты, а это влечёт за собой потери скорости на управление, которые рассчитываются по формуле:

,

где F(t) — текущая сила тяги двигателя, m(t) — текущая масса ракеты, а α(t) — угол между векторами тяги и скорости ракеты. Наибольшая часть потерь на управление ракеты Сатурн V приходится на участок полёта 2-й ступени, поскольку именно на этом участке происходит переход от вертикального полёта в горизонтальный, и вектор тяги двигателя в наибольшей степени отклоняется по направлению от вектора скорости ракеты.

Видео:Консультация к устному экзамену. Механика. Часть 2: "Движение систем"Скачать

Использование формулы Циолковского при проектировании ракет

Выведенная в конце XIХ века, формула Циолковского и сегодня составляет важную часть математического аппарата, используемого при проектировании ракет, в частности, при определении их основных массовых характеристик.

Путём несложных преобразований формулы получаем следующее уравнение:

(1)

Это уравнение дает отношение начальной массы ракеты к её конечной массе при заданных значениях конечной скорости ракеты и удельного импульса. Введём следующие обозначения:

M0 — масса полезного груза; Mk — масса конструкции ракеты; Mt — масса топлива.

Масса конструкции ракеты в большом диапазоне значений зависит от массы топлива почти линейно: чем больше запас топлива, тем больше размеры и масса ёмкостей для его хранения, больше масса несущих элементов конструкции, мощнее (следовательно, массивнее) двигательная установка. Выразим эту зависимость в виде:

, (2)

где — коэффициент, показывающий, какое количество топлива приходится на единицу массы конструкции. При рациональном конструировании этот коэффициент в первую очередь зависит от характеристик (плотности и прочности) конструкционных материалов, используемых в производстве ракеты. Чем прочнее и легче используемые материалы, тем выше значение коэффициента . Этот коэффициент зависит также от усреднённой плотности топлива (для менее плотного топлива требуются ёмкости бо́льшего размера и массы, что ведёт к снижению значения ).

Уравнение (1) может быть записано в виде:

,

что путём элементарных преобразований приводится к виду:

(3)

Эта форма уравнения Циолковского позволяет рассчитать массу топлива, необходимого для достижения одноступенчатой ракетой заданной характеристической скорости, при заданных массе полезного груза, значении удельного импульса и значении коэффициента .

Разумеется, эта формула имеет смысл, только когда значение, получающееся при подстановке исходных данных, положительно. Поскольку экспонента для положительного аргумента всегда больше 1, числитель формулы всегда положителен, следовательно, положительным должен быть знаменатель этой формулы:

0″ src=»http://spaceracexx.narod.ru/images/73f1e30181dbe9592830353feea1cebf.png» /> , иначе говоря, e^» src=»http://spaceracexx.narod.ru/images/f8f93a86a024ac98e3b0422028769cee.png» /> (4)

Это неравенство является критерием достижимости одноступенчатой ракетой заданной скорости при заданных значениях удельного импульса и коэффициента . Если неравенство не выполняется, заданная скорость не может быть достигнута ни при каких затратах топлива: с увеличением количества топлива будет возрастать и масса конструкции ракеты и отношение начальной массы ракеты к конечной никогда не достигнет значения, требуемого формулой Циолковского для достижения заданной скорости.

Пример расчёта массы ракеты

Первая космическая скорость для выбранной орбиты составляет 7759,4 м/с, к которой добавляются предполагаемые потери от гравитации 600 м/c (это, как можно видеть, меньше, чем потери, приведённые в таблице 1, но и орбита, которую предстоит достичь — вдвое ниже), характеристическая скорость, таким образом, составит м/c (остальными потерями в первом приближении можно пренебречь). При таких параметрах величина . Неравенство (4), очевидно, не выполняется, следовательно, одноступенчатой ракетой при данных условиях достижение поставленной цели невозможно.

Расчёт для двуступенчатой ракеты. Разделим пополам характеристическую скорость, что составит характеристическую скорость для каждой из ступеней двуступенчатой ракеты. м/c. На этот раз , что удовлетворяет критерию достижимости (4), и, подставляя в формулы (3) и (2) значения, для 2-й ступени получаем: т; т; полная масса 2-й ступени составляет т. Для 1-й ступени к массе полезной нагрузки добавляется полная масса 2-й ступени, и после соответствующей подстановки получаем: т; т; полная масса 1-й ступени составляет т; общая масса двуступенчатой ракеты с полезным грузом составит т. Аналогичным образом выполняются расчёты для бо́льшего количества ступеней. В результате получаем: Стартовая масса трёхступенчатой ракеты составит т. Четырёхступенчатой — т. Пятиступенчатой — т.

На этом примере видно, как оправдывается многоступенчатость в ракетостроении — при той же конечной скорости ракета с бо́льшим числом ступеней имеет меньшую массу.

Следует отметить, что эти результаты получены в предположении, что коэффициент конструктивного совершенства ракеты остаётся постоянным, независимо от количества ступеней. Более тщательное рассмотрение показывает, что это — сильное упрощение. Ступени соединяются между собой специальными секциями — переходниками — несущими конструкциями, каждая из которых должна выдерживать суммарный вес всех последующих ступеней, помноженный на максимальное значение перегрузки, которую испытывает ракета на всех участках полёта, на которых переходник входит в состав ракеты. С увеличением числа ступеней их суммарная масса уменьшается, в то время как количество и суммарная масса переходников возрастают, что ведёт к снижению коэффициента , а, вместе с ним, и положительного эффекта многоступенчатости. В современной практике ракетостроения более четырёх ступеней, как правило, не делается.

Такого рода расчёты выполняются на самом первом этапе проектирования — при выборе варианта компоновки ракеты, но и на последующих стадиях проектирования, по мере детализации конструкции, формула Циолковского постоянно используется при поверочных расчётах, когда характеристические скорости пересчитываются, с учётом сложившихся из конкретных деталей соотношений начальной и конечной массы ракеты (ступени), конкретных характеристик двигательной установки, уточнения потерь скорости после расчёта программы полёта на активном участке, и т. д., чтобы контролировать достижение ракетой заданной скорости.

🌟 Видео

Физика 10 класс (Урок№12 - Реактивное движение.)Скачать

Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать

Механика | динамика | основы реактивного движения | 3 | формула Циолковского | для взрослыхСкачать

Механика. Л 8.1. Мощность. КПД. Уравнение Мещерского. Уравнение Бернулли.Скачать

Вывод формулы Циолковского. Метод решения задач на движение тела переменной массы.Скачать

Удивительные миры Циолковского. Tsiolkovsky’s worlds of miracle. (With English subtitles).Скачать

Механика | динамика | основы реактивного движения | 2 | уравнение Мещерского | для взрослыхСкачать

Кошмар формулы Циолковского - Мыслить №137Скачать

1.4. Законы Ньютона как уравнение движения | Динамика | Александр Чирцов | ЛекториумСкачать