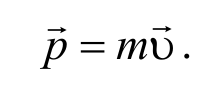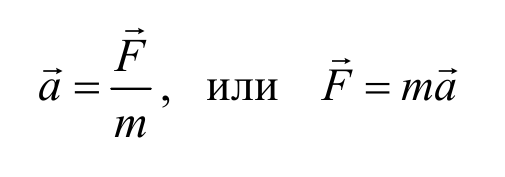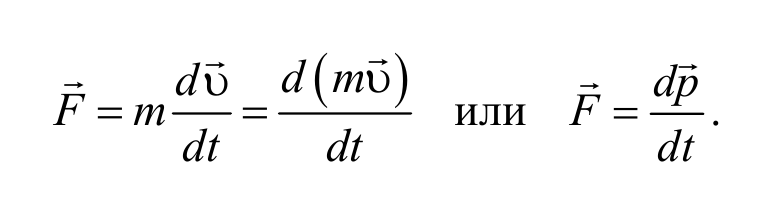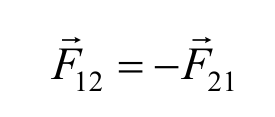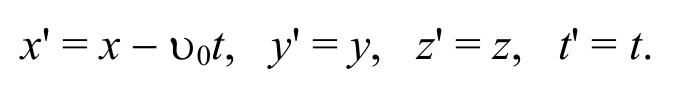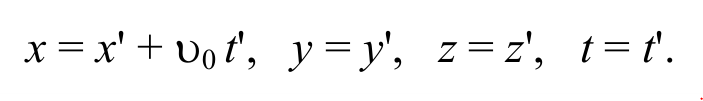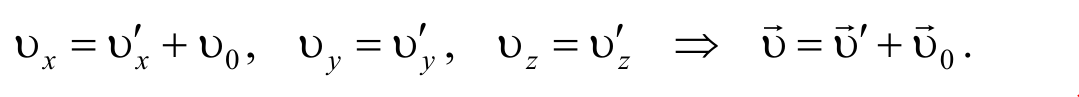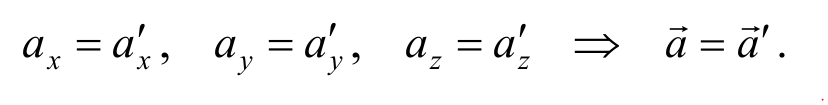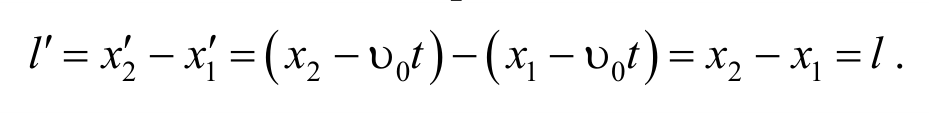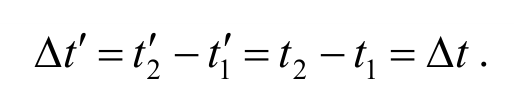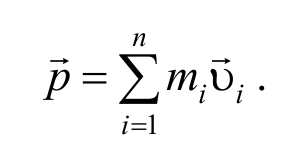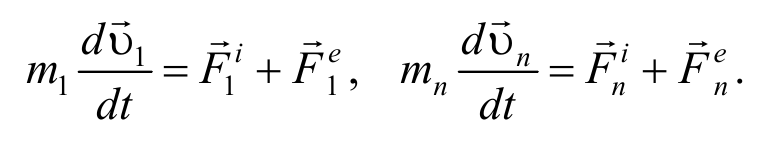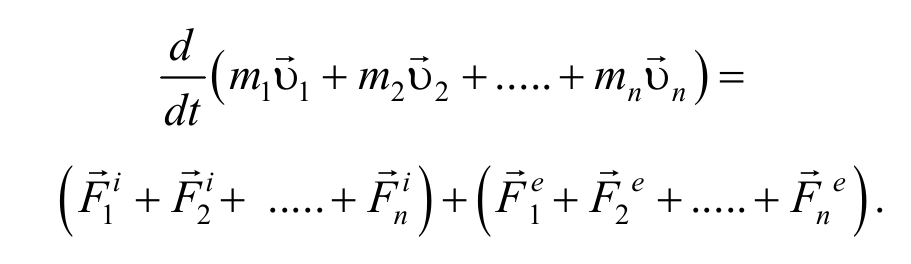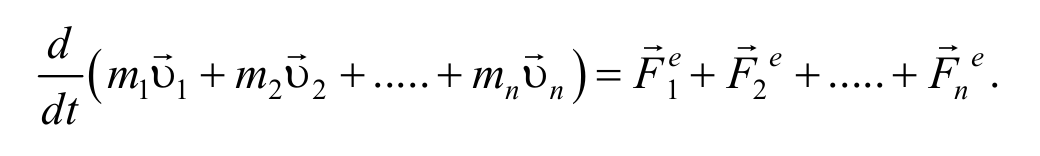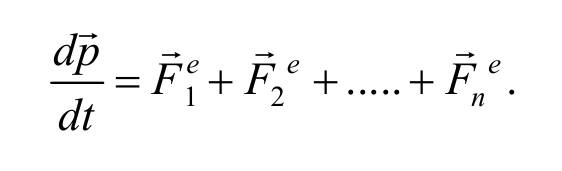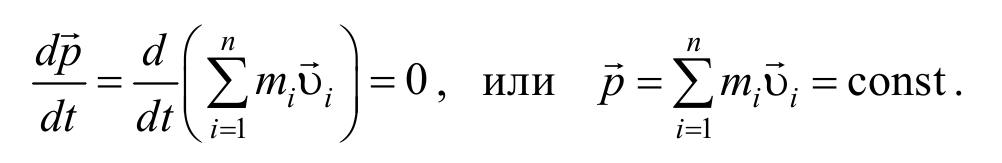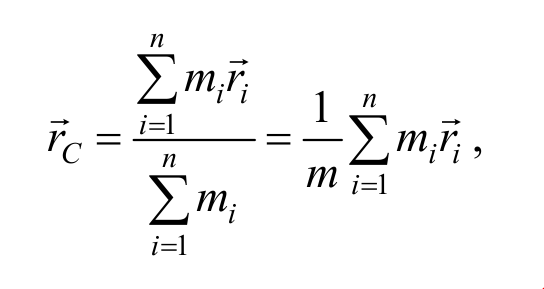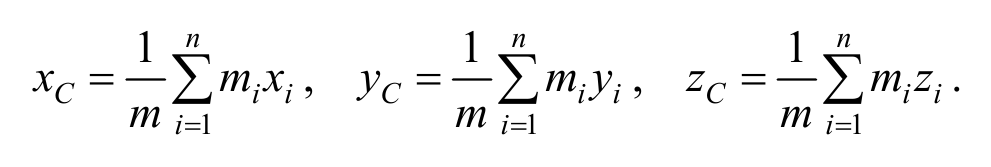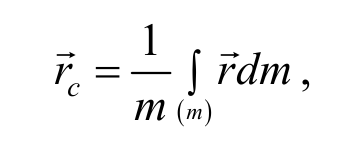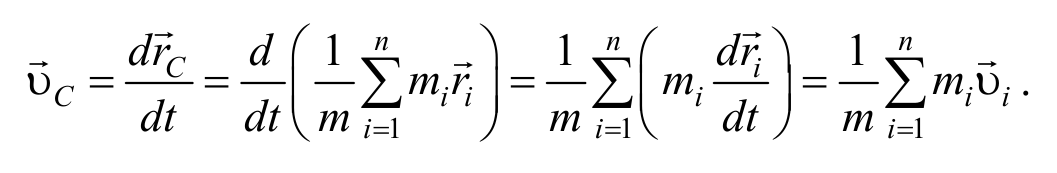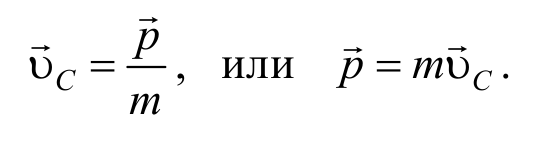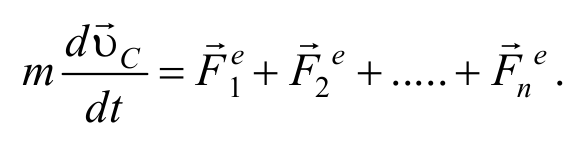Основное уравнение динамики является следствием (4 видео)

Лекция №3. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

Содержание

2.1. Основное уравнение динамики поступательного движения
2.2. Преобразования Галилея. Механический принцип относительности
2.3. Система материальных точек. Закон сохранения импульса
2.4. Центр масс. Уравнение движения центра масс
Основное уравнение динамики. Основные задачи динамики
Основное уравнение динамики, Сила.
Основное уравнение динамики
Сила, определение
📺 Видео

2.1. Основное уравнение динамики поступательного движения

Динамика − раздел механики, в котором изучается движение тел под действием приложенных сил. Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны, приложенные силы к ней со стороны окружающих тел и начальные условия, положение и скорость тела в начальный момент времени.

В основе динамики лежат три закона И. Ньютона, которые являются результатом обобщения опытных данных и теоретических сведений в области механики. Для формулировки законов динамики необходимо дать определение следующих динамических характеристик: инертность, масса, импульс тела и сила.

Инертностью (или инерцией ) называется свойство тела сохранить неизменным состояние покоя или равномерного прямолинейного движения. Количественной мерой инертности тел является инертная масса ), а количественной мерой гравитационного взаимодействия яв-ляется гравитационной массы . К настоящему времени экспериментально показано, что инертная и гравитационная массы с большой степенью точности совпадают, т. е. они эквивалентны. Этот фундаментальный закон природы называется принципом эквивалентности .

Масса − это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ является килограмм: [m] = кг . Масса − величина аддитивная, т. е. масса тела равна сумме масс всех частей этого тела.

Импульс тела (или количество движения ) − это векторная физическая величина, равная произведению массы тела на его скорость

Единица измерения импульса в СИ — $$ = $$ .

Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ − Ньютон $$ = кг× =H$$ . Сила, приложенная к телу, считается заданной, если указаны ее точка приложения, направление действия и численное значение.

Первый закон Ньютона (или закон инерции ), который формулируется следующим образом: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока действие со стороны других тел не выведут его из этого состояния. Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной . Рассмотрим две системы отсчета, двигающиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно будет двигаться с ускорением. Получается, что в одной системе отсчета первый закон Ньютона выполняется, а в другой не выполняется. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно будет также инерциальной. Системы отсчета, по отношению к которым первый закон Ньютона не выполняется, называются неинерциальными системами отсчета.

Второй закон Ньютона : ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе.

Скорость изменения импульса материальной точки равна действующей на нее силе. Уравнения (2.1.2) и (2.1.3) являются математическим выражением второго закона Ньютона. Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения .

Третий закон Ньютона : сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

2.2. Преобразования Галилея. Механический принцип относительности

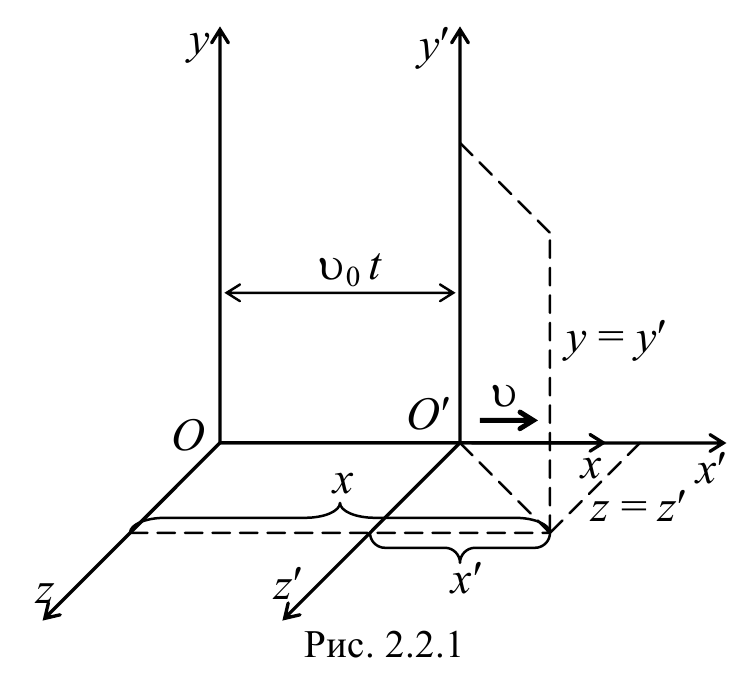
Рассмотрим две инерциальные системы XYZ (система К ) и X’Y’Z’ (система К’ ), первая из которых будет неподвижной, а вторая движется поступательно вдоль положительного направления оси 0X с постоянной скоростью υ₀ . Найдем связь между координатами х, у, z некоторой точки M в системе К и координатами х’, у’, z’ . той же точки в системе К’ . Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рис. 2.2.1 в момент времени t координаты точки М в этих системах будут связаны соотношениями

Формулы (2.2.1) называются преобразованиями Галилея для координат и времени. Они могут быть представлены также в виде обратного преобразования:

Из преобразований Галилея вытекает классический закон сложения скоростей. Продифференцировав соотношения (2.2.2) по времени, найдем связь между скоростями точки М по отношению к системам отсчета К и К’

Согласно векторному соотношению (2.2.3) скорость υ точки М относительно неподвижной системы координат (абсолютная) равна векторной сумме ее скорости υ’ относительно подвижной системы (относительная) и скорости υ₀ подвижной системы относительно неподвижной (переносная).

Продифференцировав выражение (2.2.3) по времени t , получим при условии, что υ₀ = const

Отсюда следует, что ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, оказывается одним и тем же. Поэтому, если одна из этих систем инерциальна, то и остальные будут инерциальными.

Так как масса в классической механике не зависит от скорости, то произведение массы тела на его ускорение во всех инерциальных системах будет одинаковым, т. е. вид второго закона Ньютона, описывающего движение тела, будет одинаковым во всех инерциальных системах отсчета. Неизменность выражения для закона Ньютона отражает тот факт, что все механические явления во всех инерциальных системах отсчета протекают одинаково при одинаковых условиях. Другими словами − все инерциальные системы отсчета эквивалентны между собой. Это утверждение носит название принципа относительности Галилея (или механический принцип относительности ). Он означает, что никакими опытами внутри инерциальной системы отсчета невозможно установить покоится эта система или движется равномерно и прямолинейно. Принцип относительности справедлив не только для механических, но и для любых физических явлений.

Используя преобразования Галилея, можно показать, что отрезки длин (масштабы) и интервалы времени между двумя какими-либо событиями одинаковы во всех инерциальных системах отсчета.

Понятие времени в классической механике является абсолютным, поэтому

Физические величины, не изменяющиеся при переходе от одной инерциальной системе к другой, называются инвариантными. Следовательно, отрезки длин и интервалы времени являются инвариантами классической механики.

2.3. Система материальных точек. Закон сохранения импульса

Механической системой называется совокупность материальных точек, рассматриваемых как единое целое. Силы взаимодействия между материальными точками механической системы называются внутренними . Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними . Механическая система тел, на которую не действуют внешние силы, называется замкнутой механической системой .

Импульс механической системы, представляет собой сумму импульсов всех материальных точек, входящих в механическую систему.

Рассмотрим систему материальных точек массами m₁ , m₂, …, m_n , движущихся со скоростями υ₁ , υ₂ , …, υ_n . Пусть на каждую из этих точек действуют равнодействующие внутренних сил F ₁ i , F ₂ i , …, F _n i , и равнодействующие внешних сил F ₁ e , F ₂ e , …, F _n e .

Используя второй закон Ньютона для системы точек, запишем

Сложим эти уравнения:

Согласно третьему закону Ньютона, силы, действующие между материальными точками механической системы, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

С учетом выражения (2.3.1) получим закон изменения импульса механической системы : производная по времени от импульса механической системы равна векторной сумме внешних сил, действующих на систему.

В случае замкнутой механической системы,

Выражение (2.3.6) выражает закон сохранения импульса: импульс замкнутой системы не изменяется с течением времени.

Закон сохранения импульса носит универсальный характер и выполняется также в релятивистской и квантовой механике. Закон сохранения импульса − это фундаментальный закон природы. Он является следствием определенного свойства симметрии пространства − его однородности. Под однородностью пространства понимают одинаковость свойств пространства во всех его точках.

2.4. Центр масс. Уравнение движения центра масс

В классической механике масса тела не зависит от его скорости движения, и импульс системы может быть выражен через скорость ее центра масс.

Центром масс (или центром инерции ) системы материальных точек называется воображаемая точка С , положение которой характеризует распределение массы этой системы, и радиус-вектор которой определяется выражением:

где m_i и r _i − масса и радиус-вектор i-ой точки системы; $$m = <sum_^n>m_i$$ − суммарная масса системы.

Соотношения координат центра инерции системы равны

В случае непрерывного распределения массы в системе (например, в случае протяженного тела) радиус-вектор центра масс системы определяется выражением

где r − радиус-вектор малого элемента системы, масса которого равна dm , а интегрирование проводится по всем элементам системы, т. е. по всей ее массе m .

Определим скорость центра масс механической системы

Учитывая выражение (2.3.1) получим

Таким образом, импульс механической системы равен произведению массы системы на скорость ее центра масс.

С учетом выражения (2.3.5) получим

Это выражение представляет собой закон движения центра масс : центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы, и на которую действует сила, равная векторной сумме всех внешних сил, приложенных к системе.

Закон движения центра масс показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменения скоростей этих частей, но они не могут повлиять на суммарный импульс системы и скорость ее центра масс.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Основное уравнение динамики. Основные задачи динамики

6.1. Основное уравнение динамики.

Основное уравнение динамики есть математическое выражение второго закона Ньютона:

. (6.1)

Записанное через импульс, оно имеет вид:

. (6.2)

Мы записали второй закон Ньютона как опытный закон. В то же время его можно представить как следствие закона сохранения импульса. В самом деле, если система изолирована (замкнута), то имеем

. (6.3)

Если система не изолирована (или рассматриваем отдельные тела внутри замкнутой системы), то

. (6.4)

Функцию координат и скорости материальной точки, определяющую производную ее импульса по времени называют силой. Поэтому основное уравнение динамики или 2-ой закон Ньютона записывается

или . (6.5)

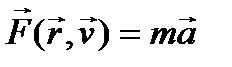
Это уравнение — векторное, поэтому оно может быть представлено в виде системы из трех (по числу измерений пространства) скалярных уравнений. Однако, в силу принципа независимости движения по взаимно перпендикулярным направлениям (осям), может сохраняться часть проекций импульса , например, на одну из осей, тогда для других проекций записываются уравнения типа (6.3). Конкретное содержание эти уравнения получают лишь тогда, когда определена функция . Установление таких зависимостей — основная задача динамики.

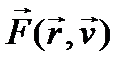
Пример: сохранение импульса по оси x: , т.е. и 1-ый закон Ньютона формально становится как бы следствием 2-го закона Ньютона.

Однако выделение 1-го закона Ньютона в “самостоятельный” физический закон принципиально необходимо, поскольку он указывает такую систему отсчета (ИСО), в которой справедлива запись 2-го закона Ньютона.

Рассмотрим образованную из двух тел замкнутую систему. В такой системе выполняется закон сохранения импульса:

Дифференцируя по времени, получаем

, или .

Т. о., мы пришли к математическому выражению 3-го закона Ньютона.

В силу того, что в замкнутой системе , получаем важное следствие.

Сумма сил, действующих внутри замкнутой системы тел (внутренних сил) равна нулю: .

6.2. Основные задачи динамики.

Два основных типа задач динамики:

1) Известна зависимость координаты от времени 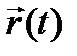, при этом находим .

2) Известна сила как функция координат и скоростей, находим .

6.3. Уравнение движения тела с переменной массой.

Во многих задачах, представляющих практический интерес, масса тела может изменяться в процессе движения.

Получим уравнение для движения тела с переменной массой, пользуясь инвариантностью законов механики, т.е. их неизменностью в различных ИСО. В качестве примера рассмотрим движение ракеты:

а) введем инерциальную 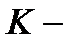систему отсчета, скорость которой совпадает со скоростью ракеты в момент времени , , т.е. в указанный момент времени ракета покоится в системе;

б) пусть в момент времени 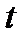ракета имеет массу ;

в) присоединяемая (отделяемая) масса имеет скорость относительно массы ;

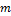
г) за время от до ракета приобретает в системе импульс , как за счет внешних сил , действующих со стороны окружающих тел или силового поля, так и за счет присоединяемой (отделяемой) массы :

. (6.6)

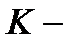
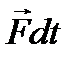
Поделив уравнение (6.6) на 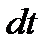, получаем уравнение Мещерского:

. (6.6,а)

Уравнение Мещерского – основное уравнение динамики тела с переменной массой. Оно описывает движение тела, к которому присоединяется масса со скоростью (Внимание: знак + в уравнении (6.6,а) – присоединение массы).

Будучи полученным в ИСО, в силу принципа относительности Галилея это уравнение справедливо в любой ИСО.

Рассмотрим частные случаи уравнения Мещерского.

А) Реактивная сила: . Если — потеря массы и выброс массы происходит в сторону, противоположную направлению движения ракета ( ), то реактивная сила вызывает ускорение ракеты (вектор направлен против вектора ).

Б) Если скорость , то и уравнение Мещерского совпадает по форме с основным уравнением динамики, но только с массой, зависящей от времени, :

. (6.7)

Пример такого движения: движение цистерны, из которой выливается вода.

В) Когда (т.е. присоединяемая масса неподвижна или отделяемая масса становится неподвижной в системе отсчета, относительно которой со скоростью движется тело), тогда

, (6.8)

, (6.9)

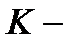
т.е. получили основное уравнение динамики, в котором как скорость, так и масса являются функциями времени.

Пример движения: движущаяся платформа, на которую сыпется песок из неподвижного бункера.

Рассмотрим движение ракеты в отсутствие внешних сил ( ). Тогда из (6.6) получаем

. (6.10)

Проекция скорости выбрасываемой ракетой газовой струи на направление движения ракеты равна .

Поэтому уравнение (6.10) приводится к виду

. (6.11)

Простейшим и наиболее важным является случай, когда скорость газовой струи постоянна на активном участке траектории (во время работы двигателей). Предположение о постоянстве скорости истечения газов, не затрагивая основные черты явления, сильно облегчает решение уравнения (6.11). В этом случае

. (6.12)

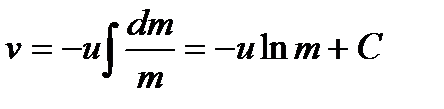
Пусть начальная скорость ракеты в некоторой инерциальной системе отсчета равна нулю, а её масса равна , т.е.

Тогда значение постоянной , определенное из начальных условий,

. (6.13)

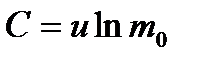
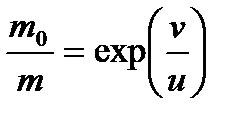
Последнее выражение носит название формулы Циолковского (Э.К. Циолковский 1857-1935 гг.).

Оно справедливо для нерелятивистских движений, т.е. для случаев, когда скорости и малы по сравнению со скоростью света в вакууме .

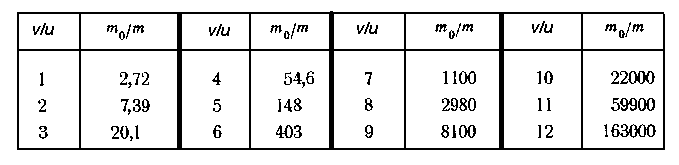
Формула Циолковского позволяет рассчитать запас топлива, необходимый для сообщения ракете определенной скорости . Результаты вычислений, проведенных по формуле (6.13) приведены в табл.

Из таблицы видно, что относительная полезная масса ракеты быстро увеличивается с ростом скорости истечения газовой струи. В молекулярной физике показывается, что скорость газовой струи пропорциональна , где абсолютная температура газа, а его молярная масса. Поэтому газы, выбрасываемые ракетой, должны иметь возможно меньший молекулярный вес и должны быть нагреты до возможно большей температуры.

В современных ракетах на химическом топливе скорость газовой струи порядка нескольких километров с секунду и, вероятно, не превосходит . Имея это в виду, можно оценить перспективы межпланетных и межзвездных полетов ракет на химическом топливе (Сивухин, I, стр. 114-122).