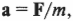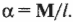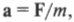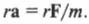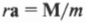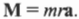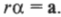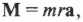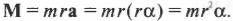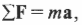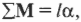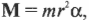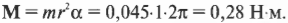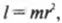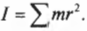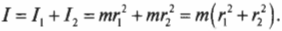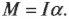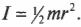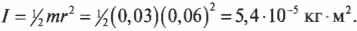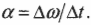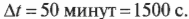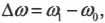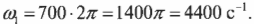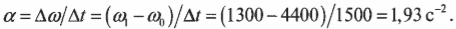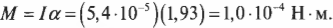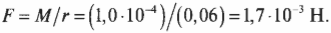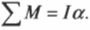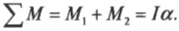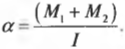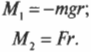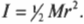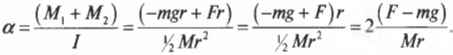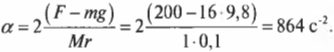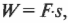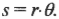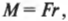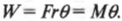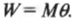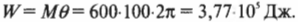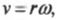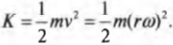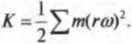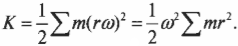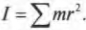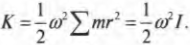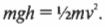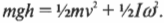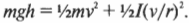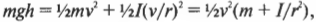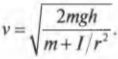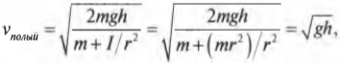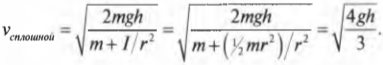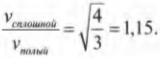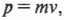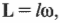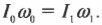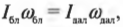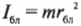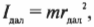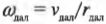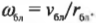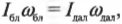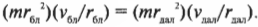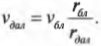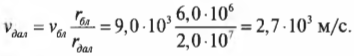Основное уравнение динамики вращательного движения как аналог второго закона ньютона

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Глава 11. Раскручиваем объекты: момент инерции

• Переходим от динамики поступательного движения к динамике вращательного движения
• Вычисляем момент инерции
• Определяем работу вращательного движения
• Находим связь между работой и изменением кинетической энергии
• Изучаем закон сохранения момента импульса

Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Применяем второй закон Ньютона для вращательного движения

Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:

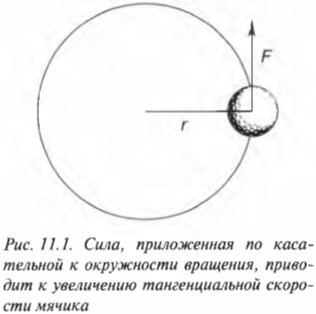
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)

то, умножая обе части этой формулы на радиус окружности ​ ( r ) ​, получим:

Поскольку ​ ( rmathbf=mathbf ) ​ то

Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ​ ( r ) ​. Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)

Преобразуем тангенциальное ускорение в угловое

Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ​ ( alpha ) ​ и тангенциальным ускорением ​ ( mathbf ) ​. Как нам уже известно из главы 10, они связаны следующим соотношением:

Подставляя это выражение в приведенную выше формулу

Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ​ ( l=mr^2 ) ​, называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.

Пример: вычисляем момент силы для обеспечения углового ускорения

Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:

где ​ ( mathbf ) ​ обозначает векторную сумму всех сил, действующих на объект.

Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:

где ( mathbf ) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м 2 .

Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ​ ( mathbf=lalpha ) ​, т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.

Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ​ ( 2pi с^ ) ​? Подставляя значения в уже известную нам формулу

Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Вычисляем момент инерции протяженного объекта

Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ​ ( r ) ​. В таком случае момент инерции имеет знакомый вид:

где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ) .

Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:

Например, момент инерции ​ ( l ) ​ системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ​ ( m ) ​ на расстояниях ​ ( r_1 ) ​ и ​ ( r_2 ) ​ равен сумме их отдельных моментов инерции ​ ( l_1=mr_1^2 ) ​ и ( l_2=mr_2^2 ) :

А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.

Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.

Пример: замедление вращения компакт-диска

Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:

Момент инерции диска с радиусом ​ ( r ) ​, вращающегося относительно своего центра в плоскости диска, выражается формулой:

Подставляя значения, получим:

Теперь нужно определить угловое ускорение, которое определяется следующей формулой:

Изменение угловой скорости ​ ( Deltaomega ) ​ произошло за промежуток времени:

В данном примере изменение угловой скорости:

где ​ ( omega_1 ) ​ — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.

Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ​ ( 2pi ) ​ радиан:

Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:

Подставляя значения в формулу углового ускорения, получим:

Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:

Итак, средний момент равен 10 -4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:

Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.

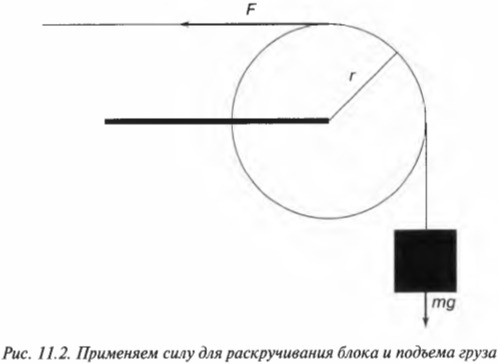
Еще один пример: поднимаем груз

Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.

В данном примере нужно вычислить сумму всех моментов сил ​ ( mathbf ) ​, которые действуют на веревку:

В данном примере на веревку действует два момента сил: один ​ ( M_1 ) ​ со стороны груза весом ​ ( mg ) ​, а другой ( M_2 ) — со стороны горизонтальной силы ​ ( F ) ​:

Отсюда получаем формулу для углового ускорения:

Эти моменты ​ ( M_1 ) ​ и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ​ ( r ) ​, поэтому:

Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:

Подставляя выражения для ​ ( l ) ​, ​ ( M_1 ) ​ и ​ ( M_2 ) ​ в формулу для углового ускорения, получим:

Подставляя значения, получим:

Видео:Лекция 06 Динамика твердого телаСкачать

Видео:Основное уравнение динамики вращательного движенияСкачать

Вычисляем энергию и работу при вращательном движении

При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.

Работа при вращательном движении

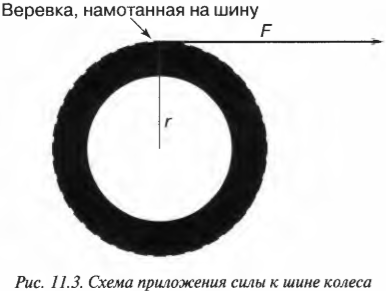
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.

Пусть шина имеет радиус ​ ( r ) ​ и для ее вращения используется сила ​ ( F ) ​, как показано на рис. 11.3.

Чему равна работа этой силы? Применим знакомую нам формулу:

где ​ ( s ) ​ — это перемещение веревки под действием этой силы. В данном примере перемещение ​ ( s ) ​ равно произведению радиуса ​ ( r ) ​ на угол поворота шины ​ ( theta ) ​:

Подставляя это выражение в формулу работы, получим:

Поскольку момент ​ ( M ) ​, создаваемой этой силой, равен:

то получаем для работы:

Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.

Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.

Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:

Полный оборот соответствует повороту на угол ​ ( 2pi ) ​. Подставляя значения в формулу, получим:

Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.

Изучаем кинетическую энергию вращательного движения

Из главы 8 нам уже известно, что объект массы ​ ( m ) ​, движущийся поступательно со скоростью ​ ( v ) ​, обладает кинетической энергией:

А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.

При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.

Как известно (см. главу 10), тангенциальная скорость ​ ( v ) ​ и угловая скорость ​ ( omega ) ​ связаны соотношением:

где ​ ( r ) ​ — это радиус окружности вращения.

Подставляя это соотношение в предыдущую формулу, получим:

Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:

Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:

Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:

Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:

Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.

Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости

Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.

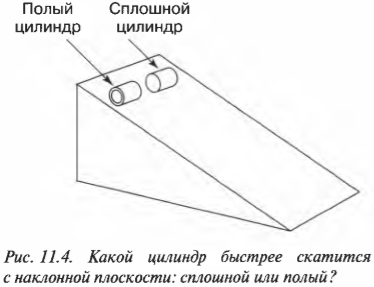
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ​ ( h ) ​ скатываются сплошной и полый цилиндры с одинаковой массой ​ ( m ) ​. Какой цилиндр достигнет нижнего конца наклонной плоскости?

Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ​ ( mgh ) ​ преобразуется в увеличение кинетической энергии только поступательного движения ​ ( ^1!/!_2mv^2 ) ​, т.е.:

Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( ^1!/!_2mv^2 ) , а часть — в кинетическую энергию вращательного движения ( ^1!/!_2Iomega ^2 ) . Тогда предыдущее равенство принимает следующий вид:

Сделаем подстановку ​ ( omega=v/r ) ​ и получим:

Путем несложных алгебраических преобразований получим:

откуда легко получить выражение для скорости цилиндра:

Для обоих цилиндров все параметры одинаковы, кроме момента инерции ​ ( I ) ​. Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ​ ( mr^2 ) ​, а сплошной — ​ ( ^1!/!_2mr^2 ) ​.

Итак, для полого цилиндра получим:

а для сплошного цилиндра:

А их отношение равно:

Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.

Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движения /05.10.2020/Скачать

Не можем остановиться: момент импульса

Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.

В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:

где ​ ( m ) ​ — это масса, a ​ ( v ) ​ — скорость материальной точки.

По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):

где ​ ( l ) ​ — это момент инерции, а ​ ( omega ) ​ — угловая скорость материальной точки.

Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.

Момент импульса в системе СИ измеряется в кг·м 2 ·с -1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.

Сохраняем момент импульса

Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ​ ( omega_0 ) ​ и его моменты инерции в позе с разведенными руками ​ ( I_0 ) ​ и в позе с сомкнутыми руками ​ ( I_1 ) ​, легко найти конечную угловую скорость ​ ( omega_1 ) ​ по формуле:

Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.

Пример закона сохранения момента импульса: вычисляем скорость спутника

Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·10 6 м от центра Плутона и имеет скорость 9·10 3 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·10 7 м от центра Плутона?

Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.

Итак, рассмотрим формулу закона сохранения момента импульса:

где ​ ( I_ ) ​ — это момент инерции спутника в самой близкой точке, ( I_ ) — это момент инерции спутника в самой далекой точке, ( omega_ ) — угловая скорость спутника в самой близкой точке, а ( omega_ ) — угловая скорость спутника в самой далекой точке.

Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:

где ​ ( r_ ) ​ — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_ ) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.

Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса

Отсюда путем несложных алгебраических преобразований, получим:

Подставляя значения, получим:

Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.

Видео:Физика. 10 класс. Основное уравнение динамики вращательного движения /08.10.2020/Скачать

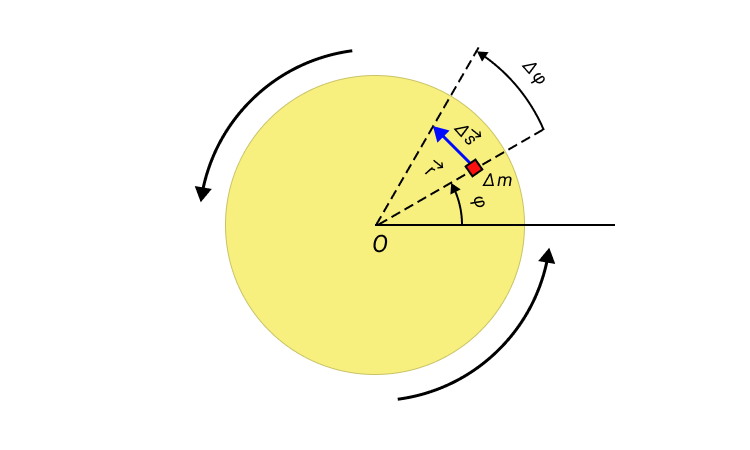
Вращение твердого тела

Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

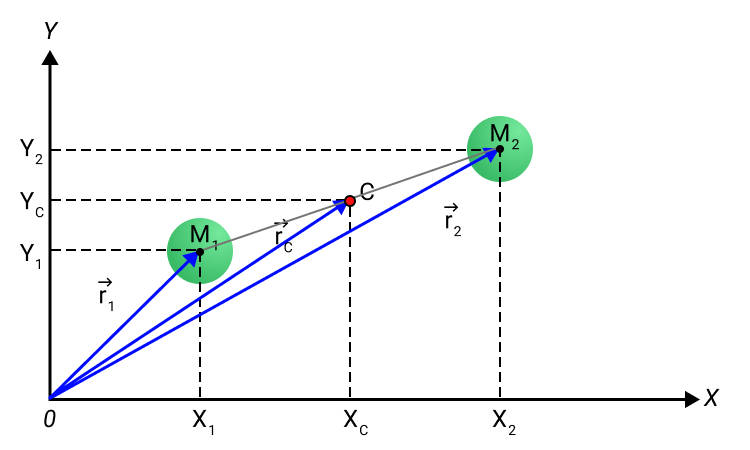
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .

Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

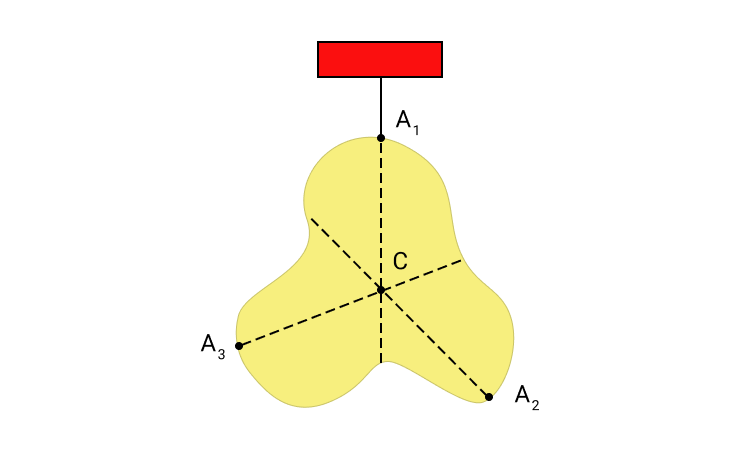
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Видео:1.4. Законы Ньютона как уравнение движения | Динамика | Александр Чирцов | ЛекториумСкачать

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Видео:Вращательное движение. 10 класс.Скачать

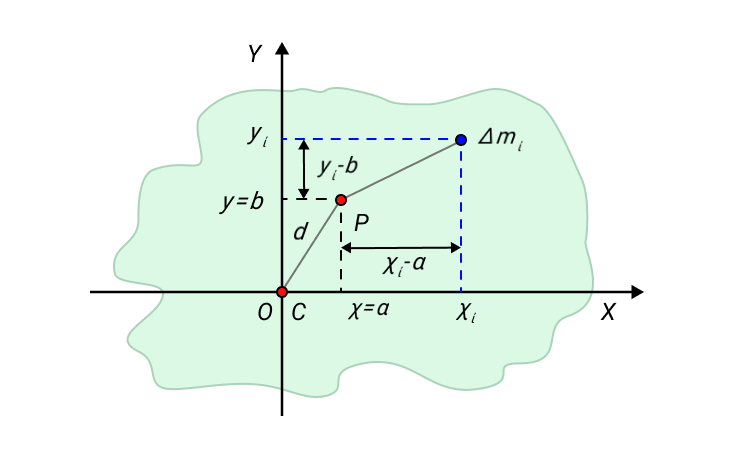
Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.

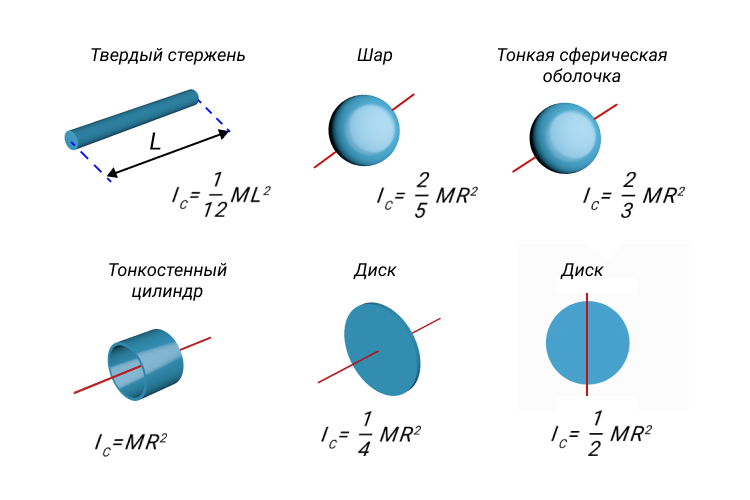
Рисунок 7. Модель момента инерции.

На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Видео:Семинар 3. Момент силы. Основное уравнение динамики вращательного движения.Скачать

Основное уравнение динамики вращательного движения твердого тела

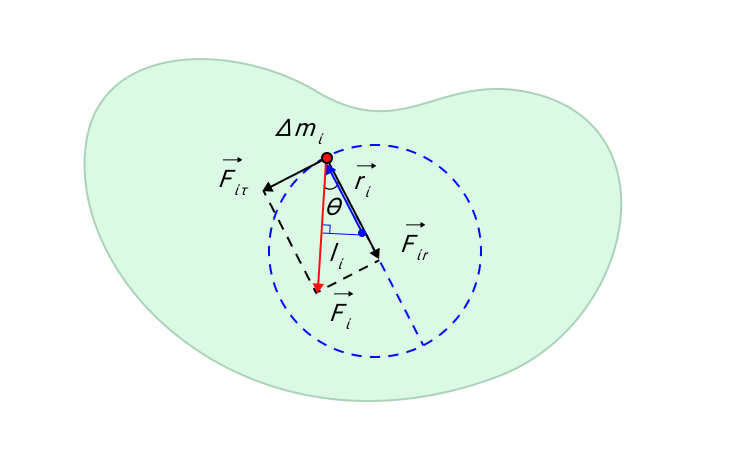
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Видео:1.3. Законы Ньютона. Часть 2 | Динамика | Александр Чирцов | ЛекториумСкачать

Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

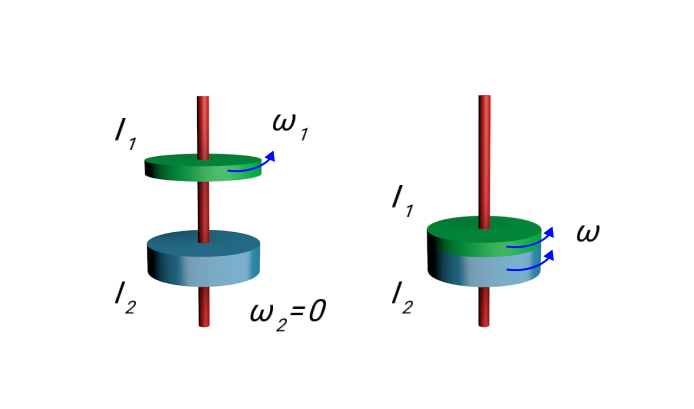
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

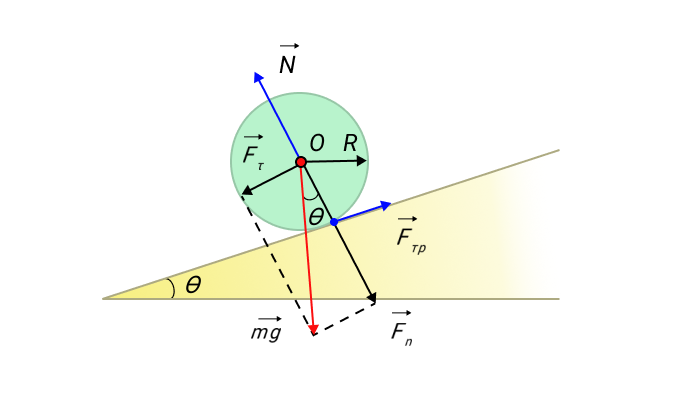
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.

Видео:Урок 94. Вычисление моментов инерции телСкачать

Вывод второго закона Ньютона для вращательного движения + примеры решения задач

Второй закон Ньютона для вращательного движения – главное тождество динамики, помогающее решить основную задачу механики для вращающегося тела: указать угол поворота тела в любой промежуток времени.

Задача механики поступательного движения считается решенной если в любое мгновение легко указать положение материальной точки относительно других тел, при условии, заданной системы отсчета.

Кроме поступательного существует вращательное движение – это такой вид движения при котором каждая точка движется по окружности, центры окружности лежат на одной прямой (оси вращения).

Характеристики вращательного движения:

• Всякая точка абсолютно твердого тела перемещается по дуге круга;
• «Ядра» окружностей расположены вдоль одной линии – ось вращения
• Разные точки передвигаются по разным траекториям;
• Зависимости перемещения по времени представляют отличные значения, изменяющиеся по направлению;
• Углы поворота точек – одинаковы.

Видео:Физика.10 класс (Урок№7 - Законы динамики Ньютона.)Скачать

Аналоги характеристик поступательного и вращательного движения

Параметры вращательного перемещения необходимо рассматривать, проводя сравнение с характеристиками поступательного.

Последовательность нахождения координат тела в любой момент времени для поступательного перемещения:

1. зная силу F находим ускорение a;
2. из ускорения находи координаты x,y,z.

Пойдем от обратного для вращательного движения:

Найти нам необходимо угла поворота – φ в любой момент времени, для этого используем угловое ускорение ε, а вот аналог силы F мы пока не знаем.

Опишем кинематику вращательного движения.

• Аналог линейной скорости во вращательном движении это угловая скорость ω — выражается отношением:

— угол поворота

• Вспомним формулу линейной скорости υ точки находящейся на вращающемся теле, для этого умножим угловую скорость ω и r — расстояние от оси до искомой точки.

Виды вращательного движения:

Поворот предмета за равные промежутки времени на одинаковые углы говорит о равномерности перемещения. Угловое ускорение отсутствует.

Уравнение движения выглядит:

— угол поворота в любой момент времени,

— начальный угол поворота

Угловая скорость постоянна, но линейная скорость постоянно изменяет направление, а это означает, что существует центростремительное ускорение, направленное по радиусу к центру окружности.

1. Неравномерное вращение

При неравномерном перемещении постоянное угловое ускорение принимает вид:

При низменном , закон изменения угловой скорости получается:

Подставляя полученные данные в формулу движения при равномерном вращении получим:

Вспомним как рассчитать угол поворота тела тремя разными способами:

Второй способ (через среднюю скорость).

Сравнение формул вращательного и поступательного перемещения наглядно представлено таблично.

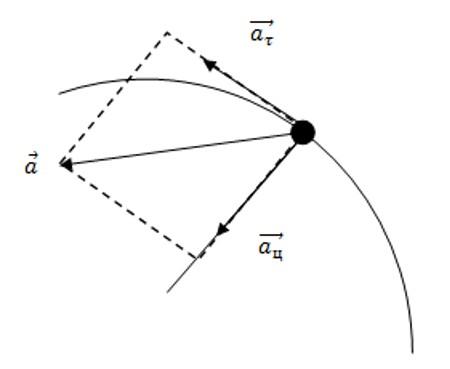
При нахождении точки на теле, неравномерно вращающемся на окружности, ускорение приобретает вид суммы:

— центростремительного и тангенциального

— тангенциального .

Сумма ускорений равна:

Тангенциальное ускорение вычисляется следующим образом

Используя связь υ и ω, получается:

Нужно сформулировать ключевые тождества, включая 2 закон сэра Ньютона для вращательного механического движения, сопутствующие обозначения, необходимые в ходе решения задач.

Видео:Урок 51. Первый закон Ньютона. Взаимодействие тел и их ускорение.Скачать

Вывод второго закона Ньютона для вращательного движения

Пусть тело, характеристиками которого можно пренебречь закреплено на невесомом стержне, 0 – ось вращения, длиной эквивалентной отрезку r.

На материальную точку оказывает воздействие силы , – реакция стержня.

— сила реакции нити;

— сила приводящая тело в движение

По II закону английского физика Исаака Ньютона второй закон динамики в векторной форме выглядит:

Выбор системы координат: Y – направляется по радиусу, Х – перпендикулярно.

Переписывая главное правило динамики в проекциях на эти оси:

Для этого на рисунке отобразим угол и выразим через него все проекции.

OX: ,

OY: ,

Из рисунка видно, что — тангенциальное ускорение, и – модуль центростремительного ускорения

Вспомним, что тангенциальное ускорение равно:

Перепишем уравнение проекции на ось x с учетом этого знания:

Вычислим угловое ускорение из полученной формулы:

Умножая на дробь на :

Далее надо визуально отобразить на рисунке rsinα.

Как видно из полученного рисунка перпендикуляр d – плечо силы F.

Сравнивая с выражением:

I=mr 2 – мера инертности тела, момент инерции.

Выходит: 2 закон Ньютона представлен для вращательного движения:

Словесная формулировка основного тождества динамики вращательного перемещения:

Алгебраическая сумма моментов сил, действующих на тело тождественно произведению момента инерции тела на его угловое ускорение.

Видео:Динамика для ОГЭ и ЕГЭ по физикеСкачать

Практическое применение второго закона Ньютона для вращательного движения

Перемещение путем вращения часто находит практическое применение. Яркие примеры:

• Колеса транспортных средств;
• Шестеренки;
• Роторы электродвигателей.

Простые «мозголомки» из школьного курса физики

Задание 1. Велосипедное колесо

Определить меру инертности у велоколеса диаметром 67 см с массой 1,3 кг? Возможно, не учитывать массу ступицы?

Колесо целесообразно разбить на N мельчайших фрагментов размером Δl с массой Δm.

Мера инертности вычисляется из выражения:

кг х м 2

Задача 2. Взаимодействие кинематики и динамики

Материальная точка перемещается по окружности, ее радиальное ускорение изменяется пропорционально четвертой степени времени. Найти n из отношения .

Записывается второй закон Ньютона для вращательного движения:

Выражая угловую скорость:

Учитывая, неизменность расстояния до центра окружности, :

Упражнение 3. Графическое представление

Одно тело вращается по зависимости 1, потом действие момента сил изменяется согласно графику 2. Нужно сравнить угловые скорости в точках A и B.

Основной закон динамики перемещения путем вращения:

Поскольку тело одно, 1/I неизменно.

Геометрический смысл интеграла – площадь криволинейных трапеций.

Случай 1:

График 2:

Результат:

Получается:

Задание 4. Шары

Два точечных шарика, обладающие равными массами скреплены тонкой невесомой спицей l. Записать выражение момента инерции системы, относительно оси, перпендикулярно соотносящейся со спицей и центром масс.

Центр оси расположен между шарами:

Мера инертности системы:

Упражнение 5. Гири

Грузы массами 2 и 1 килограмм связаны ниткой, перекинутой через блок, весящий 1 килограмм. Вычислить ускорение перемещения гирь? Рассчитать натяжение нитей?

Векторный вид поступательного передвижения:

Перемещение диска – вращение:

Первые 2 равенства надо спроектировать на Х, последнее – Y. Записать уравнение кинематической связи. Получается система:

Подставляя 4 тождество в 3:

Вычитая (2) из (1), переписывается (5):

Численное значение из выражения (6) подставляется в (1) и (2):

Практическое применение в жизни

Автомобиль

Ускорится автомобиль, если установить шины большего диаметра?

Нет. Чем больше диаметр шин, тем выше линейное ускорение. Каждый автомобиль обладает максимальным угловым ускорением, соответствующее его мощности. Мощность машины ограничена, увеличение диаметра шин приведет к снижению углового ускорения, линейное не изменится.

«Что-то странная какая-то утка, на курицу похожа…»

Домашние птицы: селезень и курица имеют одинаковую длину шага. Почему курица бегает ровно, а селезень перемещается переваливаясь?

Расстановка лап селезня шире, центр тяжести расположен дальше от опоры, поэтому при ходьбе селезень вынужден делать поворот на больший угол. Момент силы тяжести от опоры увеличивается, соответственно становится больше величины угловых ускорения и скорости.

Гонки

Европейские гонки проходят по улицам города, поэтому гонщики не снижая большой скорости совершают резкие повороты. Двигатель гоночных машин расположен посередине авто. Содержание преимущества?

Двигатель посередине авто, обладает меньшей мерой инертности относительно центра масс, поэтому поворот осуществляется при меньшем моменте сил.

Фигурное катание

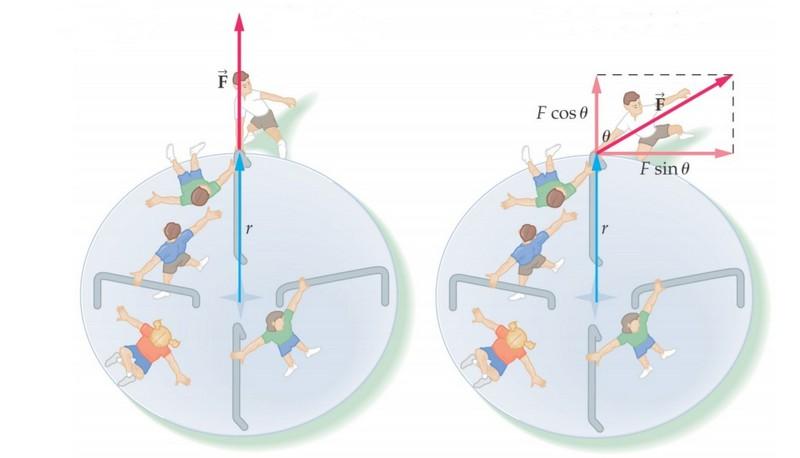
Зачем фигурист прижимает руки к телу?

Фигурист, вращаясь вокруг вертикальной оси, прижимает руки к корпусу. Момент инерции уменьшается, момент импульса остается неизменным, угловая скорость увеличивается.

Невесомость

Космонавт находится в невесомости. Как ему совершить поворот на 180˚ вокруг продольной оси?

Распутывание Гордиева узла:

Для поворота космонавт поднимает руку над головой, провоцируя поступательные движения в направлении, противоположенному повороту.

О кошках

Эмиль Кроткий утверждал: «Кошка мечтала о крыльях: ей хотелось попробовать летучих мышей». Люди не раз пытались подкидывать животное вверх ногами, при этом приземление всегда осуществляется на лапы. Момент внешних сил равен нулю, момент импульса сохраняется. Как кошке удается переворачиваться?

Момент импульса кошки, находящейся в свободном падении остается постоянным, моменты внешних сил отсутствуют. Вытягивая или прижимая к телу лапы, кошка изменяет меру инертности передней части тела относительно центральной оси от момента инерции задней части тела. Попеременно подтягивая передние или задние лапы, животное совершает поворот, ускоряющийся вращением хвоста.

Освоение 2 закона Исаака Ньютона с учетом кинематических и динамических характеристик для вращательного механического движения на практических примерах – легкое задание: надо запастись терпением, желанием приобретать знания. Изучать физику лучше вооружившись высказыванием Морихэй Уэсибы: «Двигайся, как луч света, летай, как молния, бей, как гром, вращайся вокруг устойчивого центра!»

🎬 Видео

Три Закона Ньютона. Простое ОбъяснениеСкачать

ЭТО ОБЯЗАТЕЛЬНО НУЖНО ЗНАТЬ — Второй Закон Ньютона или от чего зависит ускорение телаСкачать

Первый, второй, третий закон Ньютона. 10 класс.Скачать