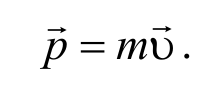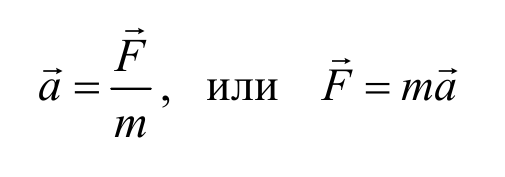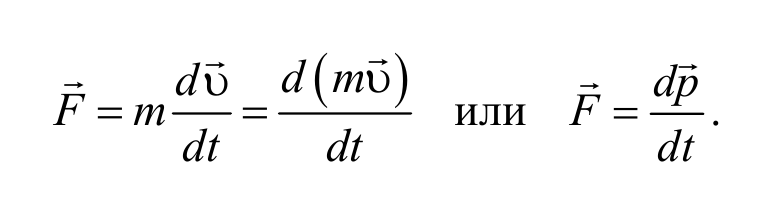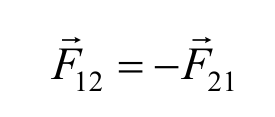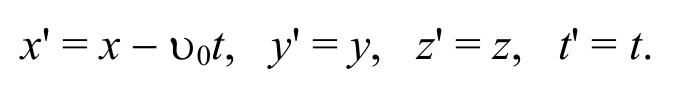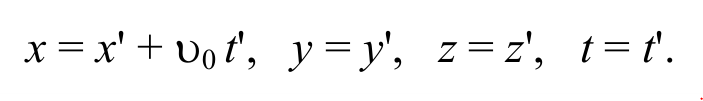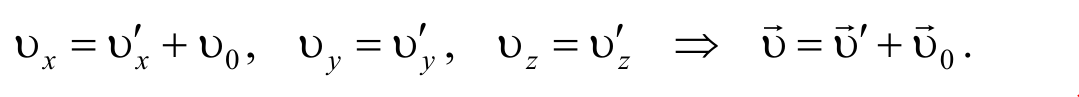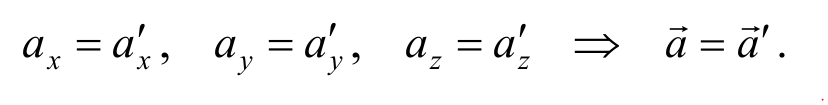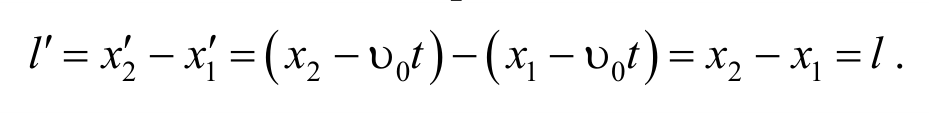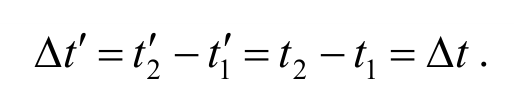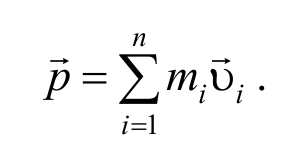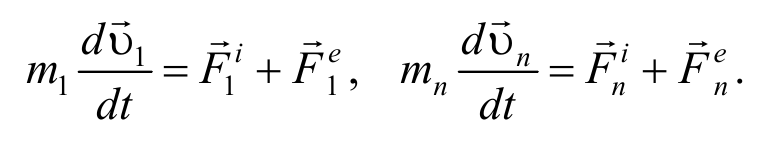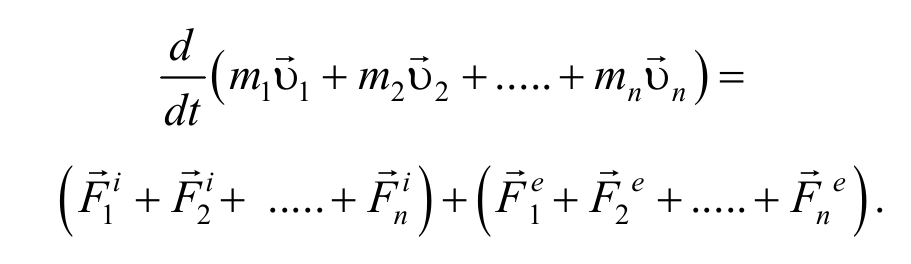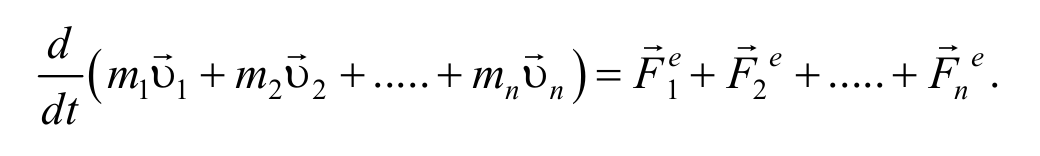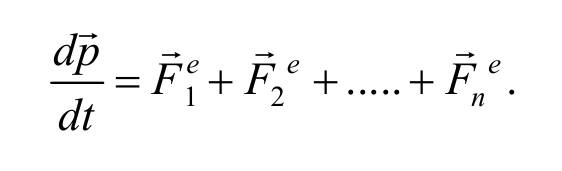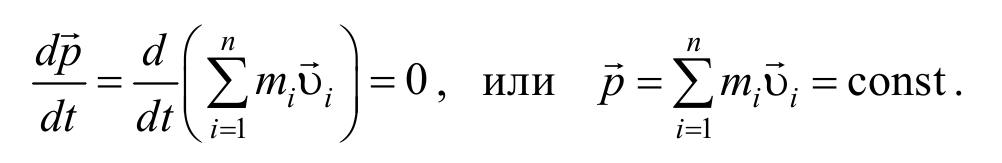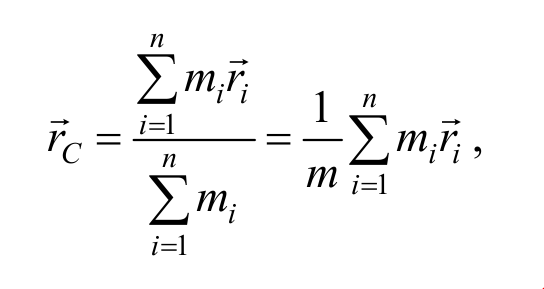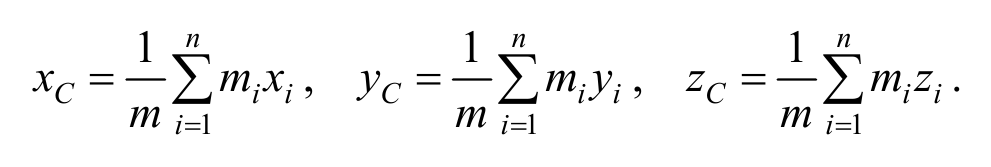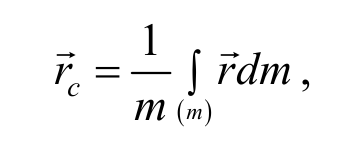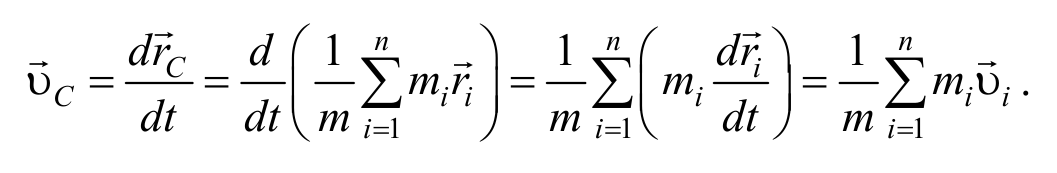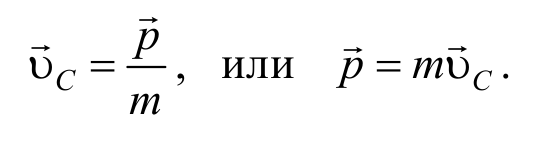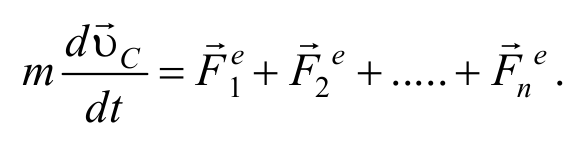Основное уравнение динамики поступательного движения

Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Лекция №3. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.1. Основное уравнение динамики поступательного движения

Динамика − раздел механики, в котором изучается движение тел под действием приложенных сил. Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны, приложенные силы к ней со стороны окружающих тел и начальные условия, положение и скорость тела в начальный момент времени.

В основе динамики лежат три закона И. Ньютона, которые являются результатом обобщения опытных данных и теоретических сведений в области механики. Для формулировки законов динамики необходимо дать определение следующих динамических характеристик: инертность, масса, импульс тела и сила.

Инертностью (или инерцией ) называется свойство тела сохранить неизменным состояние покоя или равномерного прямолинейного движения. Количественной мерой инертности тел является инертная масса ), а количественной мерой гравитационного взаимодействия яв-ляется гравитационной массы . К настоящему времени экспериментально показано, что инертная и гравитационная массы с большой степенью точности совпадают, т. е. они эквивалентны. Этот фундаментальный закон природы называется принципом эквивалентности .

Масса − это физическая величина, являющаяся мерой инерционных и гравитационных свойств тела. Единицей массы в СИ является килограмм: [m] = кг . Масса − величина аддитивная, т. е. масса тела равна сумме масс всех частей этого тела.

Импульс тела (или количество движения ) − это векторная физическая величина, равная произведению массы тела на его скорость

Единица измерения импульса в СИ — $$ = $$ .

Сила − это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение. Единица измерения силы в СИ − Ньютон $$ = кг× =H$$ . Сила, приложенная к телу, считается заданной, если указаны ее точка приложения, направление действия и численное значение.

Первый закон Ньютона (или закон инерции ), который формулируется следующим образом: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока действие со стороны других тел не выведут его из этого состояния. Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной . Рассмотрим две системы отсчета, двигающиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно будет двигаться с ускорением. Получается, что в одной системе отсчета первый закон Ньютона выполняется, а в другой не выполняется. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно будет также инерциальной. Системы отсчета, по отношению к которым первый закон Ньютона не выполняется, называются неинерциальными системами отсчета.

Второй закон Ньютона : ускорение тела прямо пропорционально результирующей сил приложенных к нему и обратно пропорционально его массе.

Скорость изменения импульса материальной точки равна действующей на нее силе. Уравнения (2.1.2) и (2.1.3) являются математическим выражением второго закона Ньютона. Второй закон Ньютона позволяет решать основную задачу механики. Поэтому его называется основным уравнением динамики поступательного движения .

Третий закон Ньютона : сила, с которой одно тело действует на другое, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

2.2. Преобразования Галилея. Механический принцип относительности

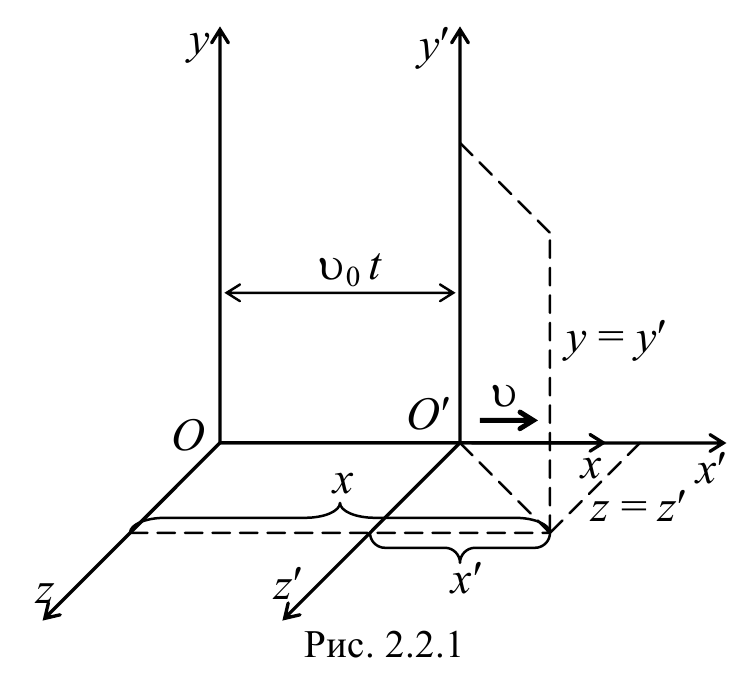
Рассмотрим две инерциальные системы XYZ (система К ) и X’Y’Z’ (система К’ ), первая из которых будет неподвижной, а вторая движется поступательно вдоль положительного направления оси 0X с постоянной скоростью υ₀ . Найдем связь между координатами х, у, z некоторой точки M в системе К и координатами х’, у’, z’ . той же точки в системе К’ . Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рис. 2.2.1 в момент времени t координаты точки М в этих системах будут связаны соотношениями

Формулы (2.2.1) называются преобразованиями Галилея для координат и времени. Они могут быть представлены также в виде обратного преобразования:

Из преобразований Галилея вытекает классический закон сложения скоростей. Продифференцировав соотношения (2.2.2) по времени, найдем связь между скоростями точки М по отношению к системам отсчета К и К’

Согласно векторному соотношению (2.2.3) скорость υ точки М относительно неподвижной системы координат (абсолютная) равна векторной сумме ее скорости υ’ относительно подвижной системы (относительная) и скорости υ₀ подвижной системы относительно неподвижной (переносная).

Продифференцировав выражение (2.2.3) по времени t , получим при условии, что υ₀ = const

Отсюда следует, что ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, оказывается одним и тем же. Поэтому, если одна из этих систем инерциальна, то и остальные будут инерциальными.

Так как масса в классической механике не зависит от скорости, то произведение массы тела на его ускорение во всех инерциальных системах будет одинаковым, т. е. вид второго закона Ньютона, описывающего движение тела, будет одинаковым во всех инерциальных системах отсчета. Неизменность выражения для закона Ньютона отражает тот факт, что все механические явления во всех инерциальных системах отсчета протекают одинаково при одинаковых условиях. Другими словами − все инерциальные системы отсчета эквивалентны между собой. Это утверждение носит название принципа относительности Галилея (или механический принцип относительности ). Он означает, что никакими опытами внутри инерциальной системы отсчета невозможно установить покоится эта система или движется равномерно и прямолинейно. Принцип относительности справедлив не только для механических, но и для любых физических явлений.

Используя преобразования Галилея, можно показать, что отрезки длин (масштабы) и интервалы времени между двумя какими-либо событиями одинаковы во всех инерциальных системах отсчета.

Понятие времени в классической механике является абсолютным, поэтому

Физические величины, не изменяющиеся при переходе от одной инерциальной системе к другой, называются инвариантными. Следовательно, отрезки длин и интервалы времени являются инвариантами классической механики.

2.3. Система материальных точек. Закон сохранения импульса

Механической системой называется совокупность материальных точек, рассматриваемых как единое целое. Силы взаимодействия между материальными точками механической системы называются внутренними . Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними . Механическая система тел, на которую не действуют внешние силы, называется замкнутой механической системой .

Импульс механической системы, представляет собой сумму импульсов всех материальных точек, входящих в механическую систему.

Рассмотрим систему материальных точек массами m₁ , m₂, …, m_n , движущихся со скоростями υ₁ , υ₂ , …, υ_n . Пусть на каждую из этих точек действуют равнодействующие внутренних сил F ₁ i , F ₂ i , …, F _n i , и равнодействующие внешних сил F ₁ e , F ₂ e , …, F _n e .

Используя второй закон Ньютона для системы точек, запишем

Сложим эти уравнения:

Согласно третьему закону Ньютона, силы, действующие между материальными точками механической системы, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

С учетом выражения (2.3.1) получим закон изменения импульса механической системы : производная по времени от импульса механической системы равна векторной сумме внешних сил, действующих на систему.

В случае замкнутой механической системы,

Выражение (2.3.6) выражает закон сохранения импульса: импульс замкнутой системы не изменяется с течением времени.

Закон сохранения импульса носит универсальный характер и выполняется также в релятивистской и квантовой механике. Закон сохранения импульса − это фундаментальный закон природы. Он является следствием определенного свойства симметрии пространства − его однородности. Под однородностью пространства понимают одинаковость свойств пространства во всех его точках.

2.4. Центр масс. Уравнение движения центра масс

В классической механике масса тела не зависит от его скорости движения, и импульс системы может быть выражен через скорость ее центра масс.

Центром масс (или центром инерции ) системы материальных точек называется воображаемая точка С , положение которой характеризует распределение массы этой системы, и радиус-вектор которой определяется выражением:

где m_i и r _i − масса и радиус-вектор i-ой точки системы; $$m = <sum_^n>m_i$$ − суммарная масса системы.

Соотношения координат центра инерции системы равны

В случае непрерывного распределения массы в системе (например, в случае протяженного тела) радиус-вектор центра масс системы определяется выражением

где r − радиус-вектор малого элемента системы, масса которого равна dm , а интегрирование проводится по всем элементам системы, т. е. по всей ее массе m .

Определим скорость центра масс механической системы

Учитывая выражение (2.3.1) получим

Таким образом, импульс механической системы равен произведению массы системы на скорость ее центра масс.

С учетом выражения (2.3.5) получим

Это выражение представляет собой закон движения центра масс : центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы, и на которую действует сила, равная векторной сумме всех внешних сил, приложенных к системе.

Закон движения центра масс показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызвать изменения скоростей этих частей, но они не могут повлиять на суммарный импульс системы и скорость ее центра масс.

Видео:1 4 Динамика поступательного движенияСкачать

Основное уравнение динамики поступательного движения

Рис. 1.3.2. Координаты центра масс системы, состоящей из двух тел массами m1 и m2

Рис. 1.3.3. Произвольная система тел с центром инерции C

Центр тяжести совпадает с центром масс (центром инерции), если g (ускорение силы тяжести) для всех тел системы одинаково.

Скорость центра инерции системы vc равна

p — импульс системы тел, vi — скорость i-го тела системы. Так как. то импульс системы тел можно определить по формуле

Импульс системы тел равен произведению массы системы на скорость её центра инерции.

1.3.6. Основное уравнение динамики поступательного движения

Тела, не входящие в состав рассматриваемой системы, называют внешними телами, а силы, действующие на систему со стороны этих тел, — внешними силами. Силы взаимодействия между телами внутри системы называют внутренними силами.

Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

2. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Уравнение динамики поступательного движения тела:

,

Где M – масса тела, – его ускорение, – сумма всех действующих на тело сил.

Импульсом тела называется произведение массы тела на его скорость: .

Закон изменения импульса:

= .

Работой силы F на перемещении Ds называется произведение проекции силы на направление перемещения на это перемещение:

Где α – угол между направлениями силы и перемещения.

Работа переменной силы вычисляется как:

A = .

Мощностью называют работу, произведенную за единицу времени: N = .

Мгновенная мощность равна скалярному произведению силы, действующей на тело, на его скорость:

N = .

Кинетическая энергия тела при поступательном движении:

,

Где M – масса тела, υ – его скорость.

Потенциальная энергия тела

– в однородном поле тяжести:

(M – масса тела, G – ускорение свободного падения, H – высота тела над точкой, в которой потенциальная энергия принимается равной нулю);

– в поле упругих сил:

EП =

(K – коэффициент жесткости упругого тела, X – смещение от положения равновесия).

В замкнутой системе частиц полный импульс системы не меняется в процессе ее движения:

Σ = Const.

В замкнутой консервативной системе частиц сохраняется полная механическая энергия:

Работа сил сопротивления равна убыли полной энергии системы частиц или тела: AConp = E1 – E2.

Примеры решения задач

Канат лежит на столе так, что часть его свешивается со стола, и начинает скользить тогда, когда длина свешивающейся части составляет 25% всей его длины. Чему равен коэффициент трения каната о стол?

Разрежем мысленно канат в месте сгиба и соединим обе части невесомой нерастяжимой нитью. Когда канат только начнёт скользить, все силы уравновесятся (так как он движется ещё без ускорения), а сила трения достигает величины силы трения скольжения, FТр = μΝ.

Условия равновесия сил:

Mg = N

FТр = T

Mg = T M

Отсюда: μMg= Mg,

Или μ =

x Y Запишем уравнения движения обоих тел:

А: M = M +

X X X В: M = M + +

В проекциях для тела А:

Для тела В по оси Х:

Если сложить уравнения (3) и (4), то получим:

–2Ma = – Mg + mg Sin a, или

A = g

Подставив это значение, например, в уравнение (3) (можно в (4)), получаем: T = Mg – Ma = Mg

Подставляем числовые значения:

A = 9,8 = = 2,45

T = 1 ∙ 9,8 = 7,35 H

Вагон массой 20 т, двигавшийся равномерно, под действием силы трения в 6 кН через некоторое время остановился. Начальная скорость вагона равна 54 км/ч. Найти: 1) работу сил трения; 2) расстояние, которое вагон пройдёт до остановки.

Работа равна приращению кинетической энергии тела:

AТр = 0 – = – ,

Знак «–» означает, что работа сил трения отрицательна, так как силы трения направлены против движения.

С другой стороны, работу силы трения можно рассчитать через произведение силы на путь:

Отсюда S = =

Подставив числовые значения:

M = 2.104 кг, FТр = 6.103 Н, υ = 15 ,

AТр = = 2,25.106 Дж = 2,25 МДж,

S = = 358 м.

Камень бросили под углом α = 60о к горизонту со скоростью υ0=15 м/с. Найти кинетическую, потенциальную и полную энергию камня: 1) спустя одну секунду после начала движения; 2) в высшей точке траектории. Масса камня M = 0,2 кг. Сопротивлением воздуха пренебречь.

Выберем ось Х – по горизонтали, а ось У – по вертикали.

υX = υ0 Cos a, (6)

a X В момент времени T модуль скорости определится из соотношения:

Высота камня над поверхностью земли в момент времени T определяется из соотношения:

H = υ0 sin a — . (8)

Находим кинетическую, потенциальную и полную энергию в момент времени T:

EK = = ( υ02 – 2 υ0 Gt sin a + g2T2),

EП = mgh = ( 2 υ0 Gt sin a – g2T2),

E = EK + EП= .

В высшей точке траектории υY = 0. Этой точки камень достигает за время = (из (7)), и максимальная высота подъёма HMax= (из (8)).

EK = = ,

EП = mghMax = ,

E = EK + EП = .

Подставляем числовые значения. В момент времени T = 1 c.

В высшей точке траектории:

На рельсах стоит платформа массой M1 = 10 т, на платформе закреплено орудие массой M2 = 5 т, из которого проводится выстрел вдоль рельсов. Масса снаряда M3 = 100 кг, его начальная скорость относительно орудия υ0 = 500 м/с. Определить скорость υX платформы в первый момент времени, если: 1) платформа стояла неподвижно, 2) платформа двигалась со скоростью υ1 = 18км/ч, и выстрел был произведён в направлении её движения, 3) платформа двигалась со скоростью υ1 = 18 км/ч, и выстрел был произведён в направлении, противоположном её движению.

Согласно закону сохранения импульса, импульс замкнутой системы до какого-либо события (в данном случае выстрела) должен быть равен её импульсу после события. За положительное выбираем направление скорости снаряда. До выстрела вся система имела импульс (M1+M2+M3)υ1, после выстрела платформа с орудием движутся со скоростью υX, их импульс (M1+M2)υX, а снаряд относительно земли движется со скоростью υ0+ υ1, его импульс M3(υ0+υ1). Закон сохранения импульса записывается так:

Отсюда υX = = υ1 – υ0.

Подставляем значения масс, υ1 и υ0:

Знак минус означает, что платформа с орудием движется противоположно направлению движения снаряда;

2) υ1 = 18 км/ч = 5 м/с,

Платформа с орудием продолжает двигаться в направлении выстрела, но с меньшей скоростью;

3) υ1 = – 18 км/ч = – 5 м/с

Скорость платформы, двигавшейся в направлении, противоположном направлению выстрела, увеличивается.

Пуля, летящая горизонтально, попадает в шар, подвешенный на лёгком жёстком стержне, и застревает в нём. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара на угол 10о.

Если пуля застревает в шаре, то удар

Абсолютно неупругий, и выполняется только закон сохранения импульса. До удара пуля имела импульс Mυ, шар импульса не имел. Непосредственно после удара пуля с шаром имеют общую скорость υ1, их импульс (M + M) υ1.

Закон сохранения импульса:

Отсюда υ1 = υ.

Шар вместе с пулей в момент удара приобрёл кинетическую энергию:

EK = υ12 = υ2 = .

За счёт этой энергии шар поднялся на высоту H, при этом его кинетическая энергия переходит в потенциальную:

EK = EП Þ = (M + M) Gh. (9)

Высоту H можно выразить через расстояние от точки подвеса до центра шара и угол отклонения от вертикали

H = L – L Cos a = L(1 – cos a).

Подставив последнее выражение в соотношение (9), получим:

A L = GL(1 – cos a),

H И определим скорость пули:

υ = .

Подставив числовые значения, получим:

υ = 1001 » 543 м/с.

Камень, привязанный к верёвке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями верёвки равны 9,8 Н.

Решение

В верхней точке траектории и сила тяжести, и сила натяжения верёвки направлены вниз.

L Уравнение движения в верхней точке имеет вид:

L Man = M = Mg + T1.

В нижней точке траектории сила тяжести направлена вниз, а сила натяжения верёвки и нормальное ускорение вверх. Уравнение движения в нижней точке:

Man = M = T2 – Mg.

По условию камень вращается с постоянной скоростью, поэтому левые части обоих уравнений одинаковы. Значит, можно приравнять правые части:

M = .

Подставляем числа: M = = 0,5 кг.

Шоссе имеет вираж с уклоном в 10° при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?

Сила, действующая на автомобиль, складывается

из силы тяжести и силы нормального давления . Сумма этих сил обусловливает нормальное ускорение автомобиля при повороте.

Из треугольника сил видно, что: = tg a.

Рассчитаем An, сократив массу

= tg a,

Отсюда υ = =41,5 м/с.

🔍 Видео

Физика. 10 класс. Основное уравнение динамики вращательного движения /08.10.2020/Скачать

Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Поступательное и вращательное движения.Скачать

Поступательное и вращательное движенияСкачать

Основное уравнение динамики вращательного движенияСкачать

Динамика поступательного движения. Алгоритм решения задач.Скачать

Физика. 10 класс. Основное уравнение динамики вращательного движения /05.10.2020/Скачать

Вращательное движение. 10 класс.Скачать

Динамика поступательного движенияСкачать

Лабораторная работа №3. Изучение и проверка основного закона динамики вращательного движенияСкачать

Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

Физика 10 класс (Урок№5 - Поступательное движение. Вращательное движение твердого тела.)Скачать

Динамика поступательного движения (реал). Решение задачи методом разделенных переменных.Скачать

Динамика поступательного и вращательного движения. Коржуев А. В.Скачать

Физика. Решение задач. Динамика поступательного движения.Скачать