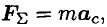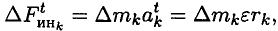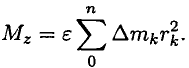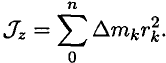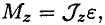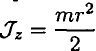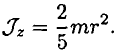Рис. 1.3.2. Координаты центра масс системы, состоящей из двух тел массами m1 и m2
Рис. 1.3.3. Произвольная система тел с центром инерции C
Центр тяжести совпадает с центром масс (центром инерции), если g (ускорение силы тяжести) для всех тел системы одинаково.
Скорость центра инерции системы vc равна
p — импульс системы тел, vi — скорость i-го тела системы. Так как. то импульс системы тел можно определить по формуле
Импульс системы тел равен произведению массы системы на скорость её центра инерции.
1.3.6. Основное уравнение динамики поступательного движения
Тела, не входящие в состав рассматриваемой системы, называют внешними телами, а силы, действующие на систему со стороны этих тел, — внешними силами. Силы взаимодействия между телами внутри системы называют внутренними силами.
- Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
- Что такое машина Атвуда?
- Уравнения динамики
- Расчет уравнений динамики для равноускоренного движения
- Проверка решения уравнений динамики
- Расчет силы тяжести
- Определение силы натяжения нити
- Основы динамики системы материальных точек
- Основы динамики системы материальных точек
- Основное уравнение динамики при поступательном движении тела
- Моменты инерции некоторых тел
- 📺 Видео
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Видео:Урок 93. Основное уравнение динамики вращательного движенияСкачать

Что такое машина Атвуда?
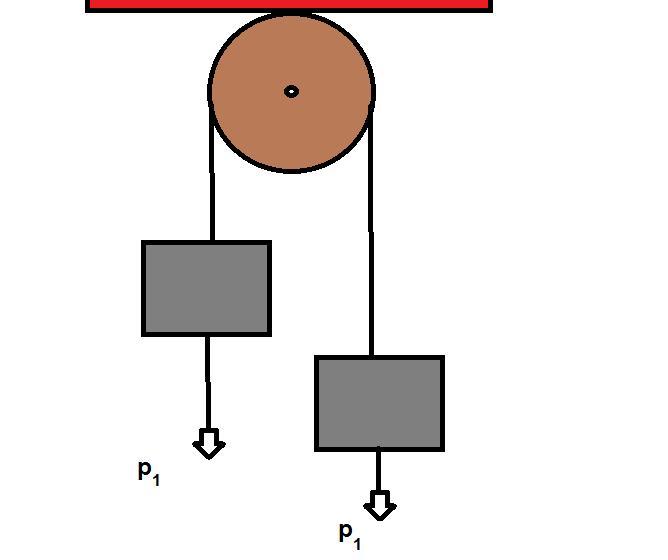
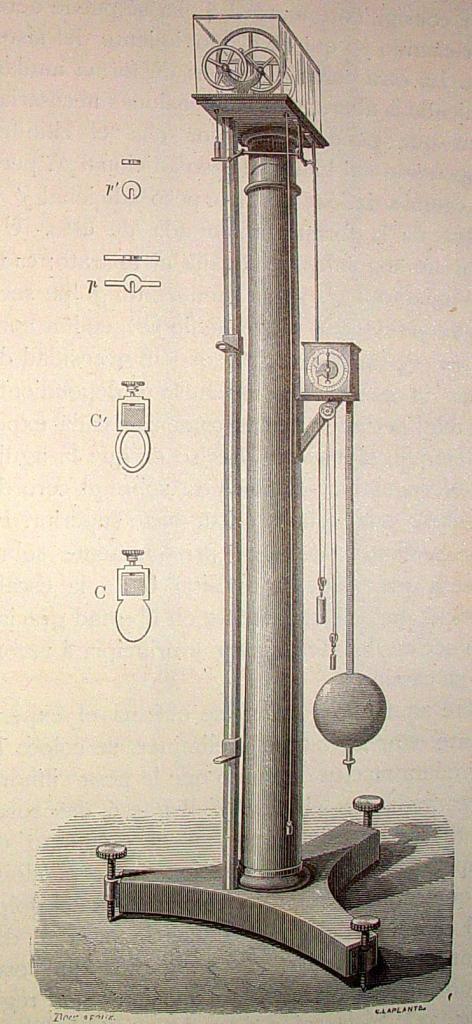
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Видео:Поступательное и вращательное движенияСкачать

Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Видео:Общее уравнение динамики. Задача 1Скачать

Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
F1 – F2 = a*(m1 + m2) =>
a = (F1 – F2)/(m1 + m2).
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
a = g*(m1 – m2)/(m1 + m2).
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Видео:Вращательное движение. 10 класс.Скачать

Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Видео:Общее уравнение динамики. Расчет механической системы.Скачать

Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Видео:Физика. 10 класс. Основное уравнение динамики вращательного движения /08.10.2020/Скачать

Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
(F1 – T)/m1 = (T – F2)/m2 =>
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
T = 2*m1*m2*g/(m1 + m2).
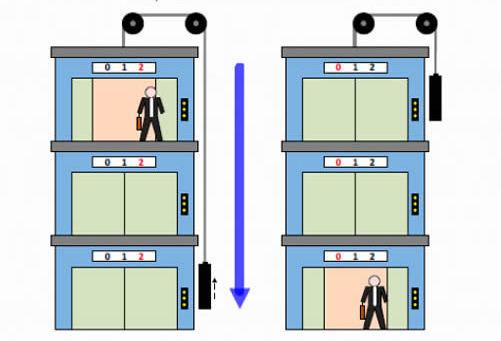
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Видео:Физика. 10 класс. Основное уравнение динамики вращательного движенияСкачать

Основы динамики системы материальных точек
Видео:Применение общего уравнения динамикиСкачать

Основы динамики системы материальных точек
Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.
Любое материальное тело в механике рассматривается как механическая система, образуемая совокупностью материальных точек.
Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения остальных точек.
Силы, действующие на точки системы, делятся на внешние и внутренние. Силы взаимодействия между точками этой системы называют внутренними. К внешним силам относятся силы, действующие со стороны точек, не входящих в эту систему.
Примерами внешних сил являются сила тяжести, сила давления, сила трения и др.
К внутренним силам относятся силы упругости.
Движение механической системы зависит не только от внешних сил, но и от суммарной массы системы 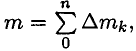
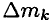
Движение системы зависит и от положения центра масс ей стемы — условной точки, в которой сосредоточена вся масса тела. Обычно считают, что в центре масс приложены все внешние силы.
Движение центра масс определяет движение всей системы толь ко при поступательном движении, при котором все точки тела дви жутся одинаково.
Основное уравнение динамики при поступательном движении тела
Для определения движения тела (системы материальных точек можно использовать второй закон динамики
где 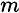
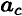
В поле земного притяжения центр масс совпадает с центров тяжести.
Основное уравнение динамики вращающегося тела
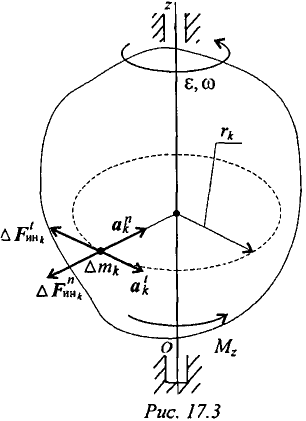
Пусть твердое тело под действием внешних сил вращается вокруг оси 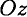
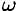
Рассматривая твердое тело как механическую систему, разобьем ее на множество материальных точек с массами 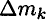
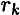
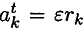
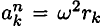
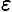
Используем для каждой точки принцип Даламбера и приложим силы инерции:
— касательную 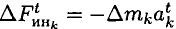
— нормальную 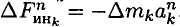
Система сил, действующих на точку, по принципу Даламбера, находится в равновесии.
Поэтому алгебраическая сумма моментов относительно оси вращения должна быть равна нулю: 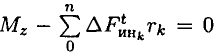
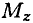
Моменты нормальных сил инерции 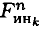
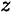
где 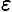
Подставив значение силы в формулу для определения моментов, получим
Величина 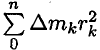
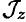
В результате получим выражение основного уравнения динамики вращающего тела:
где 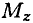
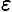
Момент инерции тела в этом выражении определяет меру инертности тела при вращении.
По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ 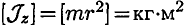
Видно, что значение момента инерции зависит от распределения массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от оси вращения. Для увеличения момента инерции используют колеса со спицами и отверстиями.
Моменты инерции некоторых тел
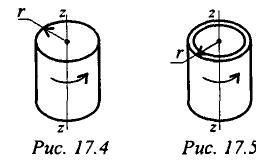
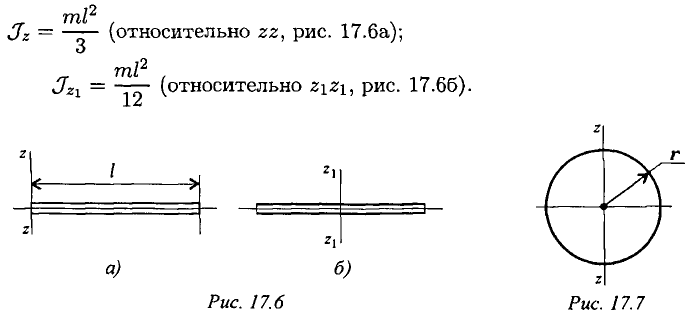
Момент инерции сплошного цилиндра (рис. 17.4)
Момент инерции полого тонкостенного цилиндра (рис. 17.5) 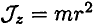
Момент инерции прямого тонкого стержня любого поперечного сечения
Момент инерции шара (рис. 17.7)
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📺 Видео
Общее уравнение динамикиСкачать

ЛР "Проверка основного уравнения динамики вращательного движения с помощью маятника Обербека"Скачать

Динамика для ОГЭ и ЕГЭ по физикеСкачать

Физика. 10 класс. Основное уравнение динамики вращательного движения /05.10.2020/Скачать

Кинематика: Поступательное и вращательное движение твёрдого тела. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Момент инерцииСкачать

Термех. Общее уравнение динамики - ч.1Скачать

Методика решения задач по динамике материальной точки. Часть 1Скачать