Основное уравнение дифракционной решетки вывод

Широкое распространение в научном эксперименте и технике получили дифракционные решетки, которые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционные решетки изготавливаются с помощью делительной машины, наносящей штрихи (царапины) на стекле или другом прозрачном материале. Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.

Рассмотрим сначала дифракцию света от решетки на примере двух щелей. (При увеличении числа щелей дифракционные максимумы становятся лишь более узкими, более яркими и отчетливыми.)

Пусть а — ширина щели, a b — ширина непрозрачного промежутка (рис. 5.6).

Рис. 5.6. Дифракция от двух щелей

Период дифракционной решетки — это расстояние между серединами соседних щелей:

Разность хода двух крайних лучей равна

Если разность хода равна нечетному числу полуволн

то свет, посылаемый двумя щелями, вследствие интерференции волн будет взаимно гаситься. Условие минимумов имеет вид

Эти минимумы называются дополнительными.

Если разность хода равна четному числу полуволн

то волны, посылаемые каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных максимумов с учетом (5.36) имеет вид

Это формула для главных максимумов дифракционной решетки.

Кроме того, в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы решетки будут наблюдаться в направлениях, определяемых условием (5.21) для одной щели:

Если дифракционная решетка состоит из N щелей (современные решетки, применяемые в приборах для спектрального анализа, имеют до 200 000 штрихов, и период d = 0.8 мкм, то есть порядка 12 000 штрихов на 1 см), то условием главных минимумов является, как и в случае двух щелей, соотношение (5.41), условием главных максимумов — соотношение (5.40), а условие дополнительных минимумов имеет вид

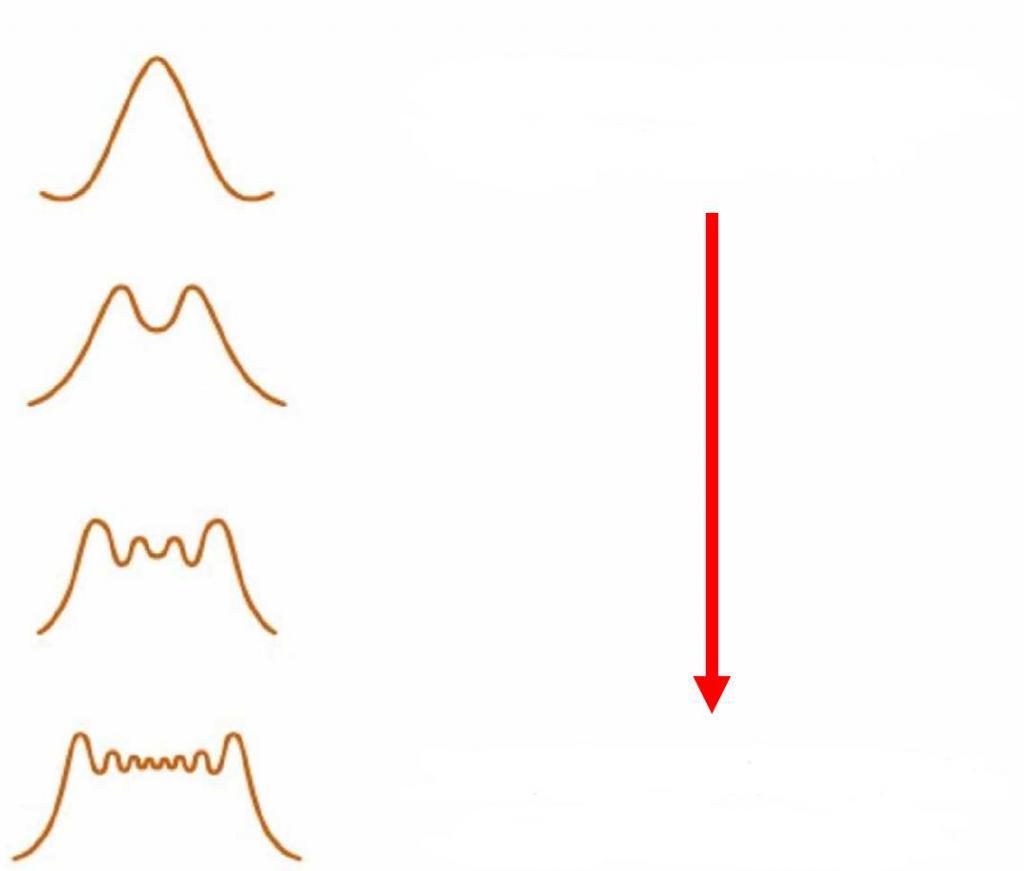
Здесь k’ может принимать все целочисленные значения, кроме 0, N, 2N, . . Следовательно, в случае N щелей между двумя главными максимумами располагается (N–1) дополнительных минимумов, разделенных вторичными максимумами, создающими относительно слабый фон.

Положение главных максимумов зависит от длины волны l. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный — наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Заметим, что в то время как спектральная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, наоборот, сильнее отклоняет красные лучи.

Важной характеристикой всякого спектрального прибора является разрешающая способность.

Разрешающая способность спектрального прибора — это безразмерная величина

Видео:Урок 420. Дифракция света. Дифракционная решеткаСкачать

Дифракционная решётка

Дифракциейназывается любое отклонение распространения света от прямолинейного, не связанное с отражением и преломлением. Качественный метод расчета дифракционной картины предложил Френель. Основной идеей метода является принцип Гюйгенса — Френеля:

Каждая точка, до которой доходит волна, служит источником когерентных вторичных волн, а дальнейшее распространение волны определяется интерференцией вторичных волн.

Геометрическое место точек, для которых колебания имеют одинаковые фазы, называют волновой поверхностью. Волновой фронт также является волновой поверхностью.

Дифракционная решеткапредставляет собой совокупность большого числа параллельных щелей или зеркал одинаковой ширины и отстоящих друг от друга на одинаковом расстоянии.Периодом решетки (d)называется расстояние между серединами соседних щелей, или что то же самое сумма ширины щели (а) и непрозрачного промежутка (b)между ними (d = a + b).

Рассмотрим принцип действия дифракционной решетки. Пусть на решетку нормально к её поверхности падает параллельный пучок лучей белого света (рис. 1). На щелях решетки, ширина которых соизмерима с длиной волны света, происходит дифракция.

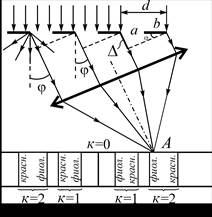Рис. 1. Ход лучей в дифракционной решетке

В результате за дифракционной решеткой согласно принципу Гюйгенса-Френеля от каждой точки щели световые лучи будут распространяться во всех возможных направлениях, которым можно сопоставить углы отклонения φ световых лучей (углы дифракции) от первоначального направления. Параллельные между собой лучи (дифрагирующие под одинаковым углом φ) можно сфокусировать, установив за решеткой собирающую линзу. Каждый пучок параллельных лучей соберется в задней фокальной плоскости линзы в определённой точке А. Параллельные лучи, соответствующие другим углам дифракции, соберутся в других точках фокальной плоскости линзы. В этих точках будет наблюдаться интерференция световых волн, исходящих от разных щелей решетки. 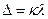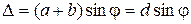Если оптическая разность хода между соответствующими лучами монохроматического света будет равна целому числу длин волн , κ = 0, ±1, ±2, …, то в точке наложения лучей будет наблюдаться максимум интенсивности света для данной длины волны, Из рисунка 1 видно, что оптическая разность хода Δ между двумя параллельными лучами, выходящими из соответствующих точек соседних щелей, равна

, (1)

где φ – угол отклонения луча решеткой.

Следовательно, условие возникновения главных интерференционных максимумов решетки или уравнение дифракционной решетки

, (2)

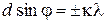
где λ – длина световой волны.

В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ = 0, κ = 0), справа и слева от которого располагаются цветные максимумы (спектральные линии) первого, второго и последующих порядков (рис. 1). Интенсивность максимумов уменьшается с ростом их порядка, т.е. с увеличением угла дифракции.

Уравнение (1) позволяет рассчитать длину волны падающего света, если измерен угол дифракции φ, для данной спектральной линии, известны период дифракционной решетки d и порядок спектра k.

Зная период решетки, можно рассчитать число штрихов n, нанесенных на 1 мм ширины решетки:

. (3)

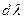
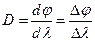
Одной из основных характеристик дифракционной решетки является её угловая дисперсия. Угловая дисперсия решетки определяет угловое расстояние dφ между направлениями для двух спектральных линий, отличающихся по длине волны на 1 нм ( = 1 нм), и характеризует степень растянутости спектра вблизи данной длины волны:

. (4)

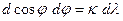
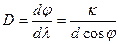
Формула для расчета угловой дисперсии решетки может быть получена при дифференцировании уравнения (2) . Тогда

. (5)

Из формулы (5) следует, что угловая дисперсия решетки тем больше, чем больше порядок спектра.

Для решеток с разными периодами ширина спектра больше у решетки, характеризующейся меньшим периодом. Обычно в пределах одного порядка 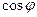меняется незначительно (особенно для решеток с небольшим числом штрихов на миллиметр), поэтому дисперсия в пределах одного порядка почти не меняется. Спектр, полученный при постоянной дисперсии, растянут равномерно во всей области длин волн, что выгодно отличает спектр решетки от спектра, даваемого призмой.

Угловая дисперсия связана с линейной дисперсией . Линей­ную дисперсию можно также вычислить по формуле

, (6) где – линейное расстояние на экране или фотопластинке между спектральными линиями, f – фокусное расстояние линзы.

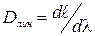
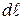
Дифракционная решетка также характеризуется разрешающей способностью. Этавеличина, характеризующая способность дифракционной решетки давать раздельное изображение двух близких спектральных линий

R = 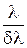, (7)

где l – средняя длина волны разрешаемых спектральных линий; dl – разность длин волн двух соседних спектральных линий.

Зависимость разрешающей способности от числа щелей дифракционной решетки N определяется формулой

R = 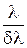= kN, (8)

где k – порядок спектра.

Из уравнения для дифракционной решетки (1) можно сделать следующие выводы:

1. Дифракционная решетка будет давать заметную дифракцию (значительные углы дифракции) только в том случае, когда период решетки соизмерим с длиной световой волны, то есть d »l» 10 –4 см. Решетки с периодом меньше длины волны не дают дифракционных максимумов.

2. Положение главных максимумов дифракционной картины зависит от длины волны. Спектральные составляющие излучения немонохроматического пучка отклоняются решеткой на разные углы (дифракционный спектр). Это позволяет использовать дифракционную решетку в качестве спектрального прибора.

3. Максимальный порядок спектра, при нормальном падении света на дифракционную решетку, определяется соотношением:

Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем и частотой штрихов, что позволяет перекрыть область спектра от ультрафиолетовой его части (l » 100 нм) до инфракрасной (l » 1 мкм). Широко используются в спектральных приборах гравированные решетки (реплики), которые представляют собой отпечатки решеток на специальных пластмассах с последующим нанесением металлического отражательного слоя.

Дата добавления: 2015-06-10 ; просмотров: 10857 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Дифракция света. Дифракционные решетки. 11 класс.Скачать

Основная формула дифракционной решетки

Одними из известных эффектов, которые подтверждают волновую природу света, являются дифракция и интерференция. Главная область их применения — спектроскопия, в которой для анализа спектрального состава электромагнитного излучения используют дифракционные решетки. Формула, которая описывает положение главных максимумов, даваемых этой решеткой, рассматривается в данной статье.

Видео:Билеты №16 и "№17 "Дифракционная решетка"Скачать

В чем заключаются явления дифракции и интерференции?

Прежде чем рассматривать вывод формулы дифракционной решетки, следует познакомиться с явлениями, благодаря которым это решетка оказывается полезной, то есть с дифракцией и интерференцией.

Вам будет интересно: Пополняем словарный запас: факир — это.

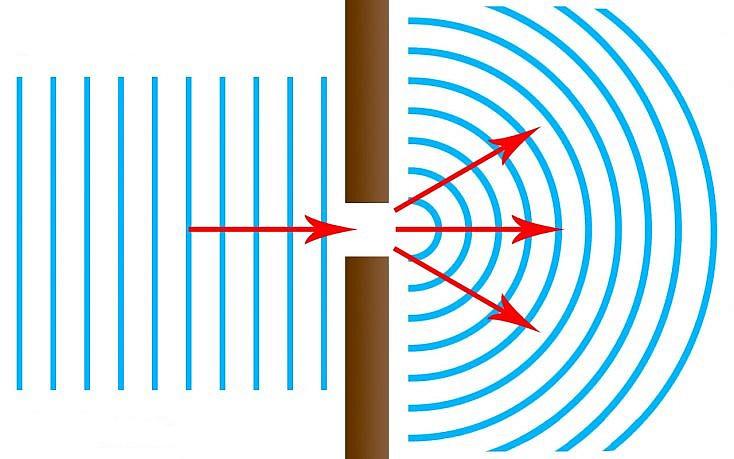
Дифракция — это процесс изменения движения волнового фронта, когда на своем пути он встречает непрозрачное препятствие, размеры которого сравнимы с длиной волны. Например, если через маленькое отверстие пропустить солнечный свет, то на стене можно наблюдать не маленькую светящуюся точку (что должно было произойти, если бы свет распространялся по прямой линии), а светящееся пятно некоторых размеров. Этот факт свидетельствует о волновой природе света.

Интерференция — еще одно явление, которое характерно исключительно для волн. Его суть заключается в наложении волн друг на друга. Если волновые колебания от нескольких источников согласованы (являются когерентными), тогда можно наблюдать устойчивую картину из чередующихся светлых и темных областей на экране. Минимумы на такой картине объясняются приходом волн в данную точку в противофазе (pi и -pi), а максимумы являются результатом попадания в рассматриваемую точку волн в одной фазе (pi и pi).

Оба описанных явления впервые объяснил англичанин Томас Юнг, когда исследовал дифракцию монохроматического света на двух тонких щелях в 1801 году.

Видео:Дифракционная решётка (видео 7) | Интерференция волн | ФизикаСкачать

Принцип Гюйгенса-Френеля и приближения дальнего и ближнего полей

Математическое описание явлений дифракции и интерференции является нетривиальной задачей. Нахождение точного ее решения требует выполнение сложных расчетов с привлечением максвелловской теории электромагнитных волн. Тем не менее в 20-е годы XIX века француз Огюстен Френель показал, что, используя представления Гюйгенса о вторичных источниках волн, можно с успехом описывать эти явления. Эта идея привела к формулировке принципа Гюйгенса-Френеля, который в настоящее время лежит в основе вывода всех формул для дифракции на препятствиях произвольной формы.

Тем не менее даже с помощью принципа Гюйгенса-Френеля решить задачу дифракции в общем виде не удается, поэтому при получении формул прибегают к некоторым приближениям. Главным из них является плоский волновой фронт. Именно такая форма волны должна падать на препятствие, чтобы можно было упростить ряд математических выкладок.

Следующее приближение заключается в положении экрана, куда проецируется дифракционная картина, относительно препятствия. Это положение описывается числом Френеля. Оно вычисляется так:

Где a — геометрические размеры препятствия (например, щели или круглого отверстия), λ — длина волны, D — дистанция между экраном и препятствием. Если для конкретного эксперимента F 1, тогда имеет место приближение ближнего поля или дифракция Френеля.

Разница между дифракциями Фраунгофера и Френеля заключается в различных условиях для явления интерференции на маленьком и большом расстояниях от препятствия.

Вывод формулы главных максимумов дифракционной решетки, который будет приведен далее в статье, предполагает рассмотрение дифракции Фраунгофера.

Видео:Дифракционные решетки с разными периодамиСкачать

Дифракционная решетка и ее виды

Эта решетка представляет собой пластинку из стекла или прозрачного пластика размером в несколько сантиметров, на которую нанесены непрозрачные штрихи одинаковой толщины. Штрихи расположены на постоянном расстоянии d друг от друга. Это расстояние носит название периода решетки. Две других важных характеристики прибора — это постоянная решетки a и число прозрачных щелей N. Величина a определяет количество щелей на 1 мм длины, поэтому она обратно пропорциональна периоду d.

Существует два типа дифракционных решеток:

• Прозрачная, которая описана выше. Дифракционная картина от такой решетки возникает в результате прохождения через нее волнового фронта.
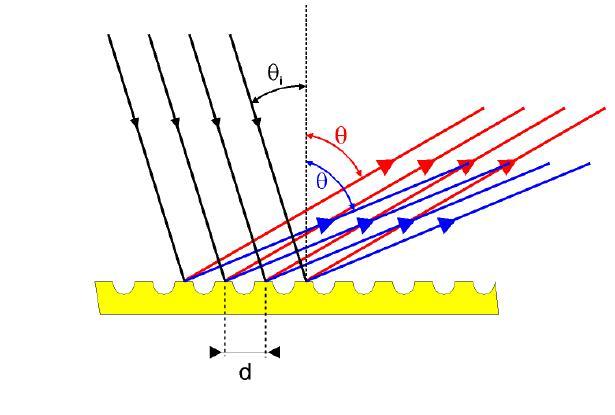
• Отражающая. Она изготавливается с помощью нанесения маленьких бороздок на гладкую поверхность. Дифракция и интерференция от такой пластинки возникают за счет отражения света от вершин каждой бороздки.

Какой бы ни был тип решетки, идея ее воздействия на волновой фронт заключается в создании периодического возмущения в нем. Это приводит к образованию большого количества когерентных источников, результатом интерференции которых является дифракционная картина на экране.

Видео:2.1 Дифракция рентгеновских лучей и обратная решёткаСкачать

Основная формула дифракционной решетки

Вывод этой формулы предполагает рассмотрение зависимости интенсивности излучения от угла его падения на экран. В приближении дальнего поля получается следующая формула для интенсивности I(θ):

I(θ) = I0*(sin(β)/β)2*[sin(N*α)/sin(α)]2, где

α = pi*d/λ*(sin(θ) — sin(θ0));

β = pi*a/λ*(sin(θ) — sin(θ0)).

В формуле ширина щели дифракционной решетки обозначается символом a. Поэтому множитель в круглых скобках отвечает за дифракцию на одной щели. Величина d — это период дифракционной решетки. Формула показывает, что множитель в квадратных скобках, где появляется этот период, описывает интерференцию от совокупности щелей решетки.

Пользуясь приведенной формулой, можно рассчитать значение интенсивности для любого угла падения света.

Если находить значение максимумов интенсивности I(θ), то можно прийти к выводу, что они появляются при условии, что α = m*pi, где m является любым целым числом. Для условия максимумов получаем:

m*pi = pi*d/λ*(sin(θm) — sin(θ0)) =>

sin(θm) — sin(θ0) = m*λ/d.

Полученное выражение называется формулой максимумов дифракционной решетки. Числа m — это порядок дифракции.

Видео:Задача №26. Дифракционная решетка | ФИЗИКА | СОТКАСкачать

Другие способы записи основной формулы для решетки

Заметим, что в приведенной в предыдущем пункте формуле присутствует член sin(θ0). Здесь угол θ0 отражает направление падения фронта световой волны относительно плоскости решетки. Когда фронт падает параллельно этой плоскости, то θ0 = 0o. Тогда получаем выражение для максимумов:

Поскольку постоянная решетки a (не путать с шириной щели) обратно пропорциональна величине d, то через постоянную дифракционной решетки формула выше перепишется в виде:

Чтобы не возникало ошибок при подстановке конкретных чисел λ, a и d в эти формулы, следует всегда использовать соответствующие единицы СИ.

Видео:7.9 Дифракционная решёткаСкачать

Понятие об угловой дисперсии решетки

Будем обозначать эту величину буквой D. Согласно математическому определению, она записывается следующим равенством:

Физический смысл угловой дисперсии D заключается в том, что она показывает, на какой угол dθm сместится максимум для порядка дифракции m, если изменить длину падающей волны на dλ.

Если применить это выражение для уравнения решетки, тогда получится формула:

Дисперсия угловая дифракционной решетки определяется по формуле выше. Видно, что величина D зависит от порядка m и от периода d.

Чем больше дисперсия D, тем выше разрешающая способность данной решетки.

Видео:Дифракция света ● 1Скачать

Разрешающая способность решетки

Под разрешающей способностью понимают физическую величину, которая показывает, на какую минимальную величину могут отличаться две длины волны, чтобы их максимумы на дифракционной картине появлялись раздельно.

Разрешающая способность определяется критерием Рэлея. Он гласит: два максимума можно разделить на дифракционной картине, если расстояние между ними оказывается больше полуширины каждого из них. Угловая полуширина максимума для решетки определяется по формуле:

Разрешающая способность решетки в соответствии с критерием Рэлея равна:

Δθm>Δθ1/2 или D*Δλ>Δθ1/2.

Подставляя значения D и Δθ1/2, получаем:

Это и есть формула разрешающей способности дифракционной решетки. Чем больше число штрихов N на пластинке и чем выше порядок дифракции, тем больше разрешающая способность для данной длины волны λ.

Видео:Урок 381. Принцип Гюйгенса. Вывод законов отражения и преломления волнСкачать

Дифракционная решетка в спектроскопии

Выпишем еще раз основное уравнение максимумов для решетки:

Здесь видно, что чем больше длина волны падает на пластинку со штрихами, тем при больших значениях углов будут появляться максимумы на экране. Иными словами, если через пластинку пропустить немонохроматический свет (например, белый), то на экране можно видеть появление цветных максимумов. Начиная от центрального белого максимума (дифракция нулевого порядка), дальше будут появляться максимумы для более коротких волн (фиолетовый, синий), а затем для более длинных (оранжевый, красный).

Другой важный вывод из этой формулы заключается в зависимости угла θm от порядка дифракции. Чем больше m, тем больше значение θm. Это означает, что цветные линии будут сильнее разделены между собой на максимумах для высокого порядка дифракции. Этот факт уже был освящен, когда рассматривалась разрешающая способность решетки (см. предыдущий пункт).

Описанные способности дифракционной решетки позволяют использовать ее для анализа спектров излучения различных светящихся объектов, включая далекие звезды и галактики.

Видео:Решение задач на дифракционную решетку 11 класс. Подготовка к ЕГЭСкачать

Пример решения задачи

Покажем, как пользоваться формулой дифракционной решетки. Длина волны света, которая падает решетку, равна 550 нм. Необходимо определить угол, при котором появляется дифракция первого порядка, если период d равен 4 мкм.

Угол θ1 легко рассчитать по формуле:

Переводим все данные в единицы СИ и подставляем в это равенство:

θ1 = arcsin(550*10-9/(4*10-6)) = 7,9o.

Если экран будет находиться на расстоянии 1 метр от решетки, то от середины центрального максимума линия первого порядка дифракции для волны 550 нм появится на расстоянии 13,8 см, что соответствует углу 7,9o.

💥 Видео

Урок 421. Задачи на дифракцию света - 1Скачать

Изучение дифракции света на дифракционной решётке (лабораторная работа О5)Скачать

Дифракционная решетка. Решение задач по формуле дифракционной решетки. Физика 11 класс.Скачать

16.2 Главные максимумы дифракционной решетки.Скачать

ЕГЭ Физика Дифракционная решетка. Решение задачСкачать

Двумерные дифракционные решеткиСкачать

Дифракционная решетка Лекция 15Скачать

Дифракционная решётка и дисперсия. Подготовка к ЕГЭ по физике | Николай Ньютон. ТехноскулСкачать

Дифракция света. Дифракционная решетка | Физика 11 класс #31 | ИнфоурокСкачать