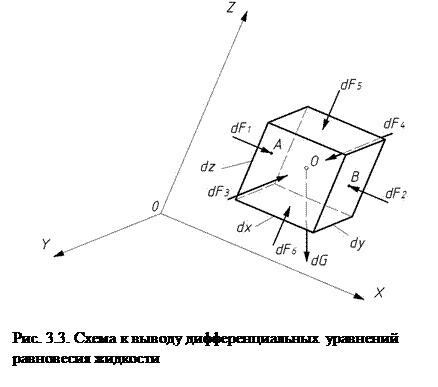
В покоящейся однородной жидкости расположим декартовы оси координат произвольным образом. В первом квадранте выделим элементарный объем в виде параллелепипеда с ребрами dx, dy и dz, параллельными соответствующим осям координат (рис. 3.3). Предположим, что жидкость в нем затвердела. Тогда на грани параллелепипеда действуют силы давления dF1…6 от окружающей жидкости, а в его центре масс (точка О) приложена равнодействующая всех массовых сил dG. Для покоящейся жидкости dG является силой тяжести. При таких допущениях условия равновесия не нарушаются. Рассмотрим условия равновесия данного параллелепипеда для оси Х:
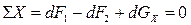
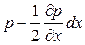
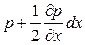
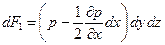
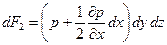
Равнодействующая всех массовых сил dG равна:
где j – ускорение, вызванное силой dG.
Тогда проекция dG на ось Х будет иметь вид:
Подставим соответствующие значения проекций сил в уравнение (3.7) и разделим на ρ dx dy dz. В результате получим:
Проведя аналогичные рассуждения для осей Y и Z получим дифференциальные уравнения равновесия жидкости Эйлера:

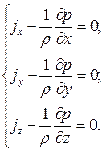
Для удобства практического использования вместо системы уравнений (3.8) получим одно эквивалентное уравнение. Для этого умножим первое уравнение системы (3.8) на dx, втрое – на dy , третье – на dz и сложим эти уравнения. В результате получим:
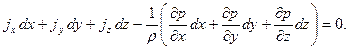
Трехчлен, находящийся в скобках, является полным дифференциалом давления dp (см. 3.3). С учетом этого уравнение (3.9) примет вид:
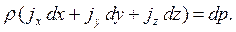
Уравнение (3.10) получено Эйлером в 1755 г. называют дифференциальным уравнением равновесия жидкости или основным уравнением гидростатики в дифференциальной форме.
Уравнение (3.10) справедливо также и для газа при совместном использовании с уравнением Клапейрона – Менделеева (2.12).
Дата добавления: 2016-01-26 ; просмотров: 1770 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Диф-ые уравнения равновесия жидкости.

Первый вариант соответствует абсолютному покою или равномерному движению сосуда с жидкостью. Такой вариант рассматривался при выводе основного уравнения гидростатики.
Второй вариант – вращение сосуда с жидкостью с постоянной угловой скоростью Й вокруг центральной оси. Несмотря на то, что вся масса жидкости вращается вместе с сосудом, частицы жидкости друг относительно друга не перемещаются, следовательно, весь объём жидкости, как и в первом случае, представляет собой как бы твёрдое тело. Давление в каждой точке жидкости не меняется во времени и зависит только от координат. По этим причинам жидкость подпадает под определение покоящейся.
Третий вариант аналогичен второму, только вращение осуществляется вокруг произвольно расположенной вертикальной оси. Во втором и третьем случае свободная поверхность жидкости принимает новую форму, соответствующую новому равновесному положению жидкости.
В четвёртом варианте сосуд с жидкостью движется прямолинейно и равноускоренно. Такой случай проявляется, например, в процессе разгона или остановки автоцистерны с жидкостью. В этом случае жидкость занимает новое равновесное положение, свободная поверхность приобретает наклонное положение, которое сохраняется до изменения ускорения. Частицы жидкости друг относительно друга находятся в покое, и давление зависит только от координат.
11. Основное уравнение гидростатики.Основным законом (уравнением) гидростатики называется уравнение [1] :
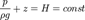



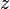

12-13. Геометрический и энергетический смысл основного уравнения гидростатики.
Геометрический смысл уравнения 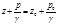
— величина z фиксирует положение точки по отношению к плоскости хОу, называемой плоскостью сравнения.
— ординату z называют высотой положения, или геометрической высотой.
При р = р0 имеем z = z0.
Очевидно, что величина р/у имеет линейную размерность.
Она представляет собой высоту, на которую жидкость может подняться под влиянием давления. Эту высоту можно измерить. если поместить в жидкость вертикальную закрытую сверху трубку, из которой полностью выкачан воздух.
Высоту р/у называют высотой давлен и я, или приведенной высотой.
Она представляет собой высоту столба жидкости, вес которого при давлении, равном нулю на его свободной поверхности, уравновешивает давление в данной точке жидкости.
Чтобы пояснить энергетический смысл членов уравнения (4), введем понятие удельной энергии. Энергию, отнесенную к единице веса жидкости, называют удельной энергией.
Размерность удельной энергии равна размерности энергии (работы), деленной на размерность силы.Единица удельной энергии [Е] — м. Часть удельной потенциальной энергии частицы жидкости, зависящая только от ее положения относительно условной горизонтальной плоскости, количественно равной z, называется удельной энергией положения частицы.
Часть удельной потенциальной энергии частицы жидкости, зависящую только от ее давления, количественно равную р/у, называют удельной энергией давления частицы
Сумма 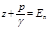
Наряду с этими понятиями в гидравлике широко используется понятие напора.
Так, величину z называют геометрическ и м напором в данной точке жидкости, а сумму z+р/γ=Н — гидростатическим напором.
Перепишем уравнение (3) в виде
p — p0 = γ (z0 — z) = γh откуда
p = p0 + γh , (5)
где h — глубина погружения частицы жидкости под ее поверхность.
Это уравнение, так же как и (4), называют основным уравнением гидростатики. Разница между ними только в системе отсчета вертикальных расстояний (z и h).
Форма уравнения (4) удобна при изучении движения жидкости, так как сумма z + р/γ входит в уравнение движения жидкости.
Форма уравнения (5) удобна в расчетах давления на поверхности и в методике измерения давления в жидкости.
Величина р является абсолютным, или полным, давлением, р0 — внешним (начальным) давлением. Произведение γh — вес столба жидкости высотой h с площадью основания, равной единице.
Поэтому γh можно назвать весовым давлением.Единицей давления, входящего в формулу (5), является паскаль (Па).
14. Закон Паскаля. Закон Паскаля формулируется так:Давление,производимое на покоящуюся жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям.Гидростатическое давление жидкости зависит от плотности р жидкости, от ускорения g свободного падения и от глубины h, на которой находится рассматриваемая точка. Оно не зависит от формы столба жидкости. Глубина h отсчитывается по вертикали от рассматриваемой точки до уровня свободной поверхности жидкости.В условиях невесомости гидростатическое давление в жидкости отсутствует, так как в этих условиях жидкость становится невесомой. Внешнее давление характеризует сжатие жидкости под действием внешней силы. Оно равно: 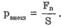
15.Избытачное и вакууметрическое давление.
Вакууметрическое давление: если абсолютное давление в точке атмосферного, то это превышение называется избыточным (нанометрическим) давлением. 
16.Поверхность равного давления. Выделим в ж-ти, к. нах-ся в равновесии, бесконечно малый объем в виде параллелепипеда с ребрами dx,dy,dz. Складывая сумму проекций сил давления, массовых сил(X- проекция массовой силы на ось)на рассматриваемую ось, получим: pdydz-(p+d1pdx/d1x)dydz+ ρdxdydzX=0 После упрощения: (-d1p/ ρd1x)+X=0 Аналогично:(-d1p/ ρd1y)+Y=0, (-d1p/ ρd1z)+Z=0 Почленно умножив 1е ур-е на ρdx, 2е на ρdy, 3е на ρdz, получим основное ур-е гидростатики: dp= ρ(Xdx+Ydy+Zdz)[1]. В общем виде это ур-е интегрируется так: p=ρП+С, где П- некоторая потенциальная ф-я. В частных случаях в зависимости от конкретных Z,X,Y находим значение П,С и p. Из [1] можно получить ур-е для пов-ти равного давления. При p=const, ρ=const, dp=0 и тогда Xdx+Ydy+Zdz=0
17.Сила давления жидкости на плоские поверхности.Угол=90 градусов, ж-ть давит на пов-ть с площ. ω во всех точках, но давление неравномерное (в верхних
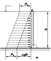
Эпюра абсолютного гидростатического давления представляет собой трапецию, а эпюра избыточного — треугольник (рис. а).
Если плоская стенка, на которую действует жидкость, наклонена к горизонту под углом a (рис. б), то основное уравнение гидростатики принимает следующий вид:
Таким образом, эпюры абсолютного и избыточного гидростатического давления на наклонную стенку представляют собой соответственно наклонную трапецию и наклонный треугольник.
Если плоская стенка, на которую с двух сторон оказывает воздействие жидкость, вертикальна, то на нее будут действовать параллельные и противоположно направленные силы гидростатического давления. Эпюра гидростатического давления на вертикальную стенку представляет собой вертикальную трапецию.
Эпюра гидростатического давления на горизонтальное дно резервуара представляет собой прямоугольник, так как при постоянной глубине избыточное давление на дно постоянно.
19. Сила давления жидкости на криволинейные поверхности
При определении силы давления жидкости на криволинейные поверхности заранее неизвестны:
*координаты точки приложения этой силы;
*направление действия рассчитываемой силы.
Поэтому в данном случае расчет силы давления проводится путем геометрического сложения ранее определенных ее трех составляющих. Каждая из составляющих параллельна одной из координатных осей:
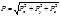
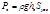
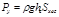
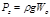
где 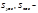
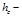
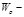
Тело давления – объем жидкости, заключенный между криволинейной поверхностью, ее проекцией на пьезометрическую плоскость (свободную поверхность) и вертикальными проектирующими плоскостями, проходящими через границы криволинейной поверхности.
Тело давления может принимать как знак плюс, так и минус. Соответственно и составляющая 
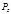
Тело давления, заполняемое жидкость, называется действительным, в отличие от фиктивного тела давления, которое заполняется жидкостью условно. Фиктивное тело давления иногда называют телом выпора.
Если на часть криволинейной поверхности жидкость давит сверху вниз, а на другую часть снизу вверх, то тело давления определяется как сумма тел давления на каждую часть криволинейной поверхности с соответствующими знаками.
На практике криволинейные поверхности часто являются цилиндрическими. Это поверхности:
*труб водопровода и канализации;*резервуаров;*сегментных затворов.
В случаях цилиндрической поверхности, когда ось у параллельна образующей криволинейной поверхности 
Направление равнодействующей силы давления характеризуется углом наклона ее к горизонту 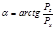
20. Сила давления жидкости на цилиндрические поверхности.
Рассмотрим давление жидкости на цилиндрическую поверхность.
В этом случае достаточно знать горизонтальную Рги вертикальную составляющую Рвсилы Р.


Суммарное давление на элементарную площадь dFравно:dР = p dF
Разложим его на горизонтальную dРги вертикальную dРвсоставляющие. Получим:
dРг = dP ∙ cos α = p dF ∙ cos α
где α — угол между направлением сил dРи dРг
Принимаем во внимание только избыточное давление:
Рг = γh dF ∙ cos α,где h —расстояние по вертикали, показанное на рисунке.
Величина dF соs α = dFв -проекция элементарной площади dF на вертикальную площадь, поэтому:dPг = γh dFвоткуда: 
где hс — расстояние от поверхности жидкости до центра тяжести фигуры Fв, представляющей собой вертикальную проекцию цилиндрической поверхности.Из формулы (1) следует: горизонтальная составляющая суммарного давления жидкости на цилиндрическую поверхность равна суммарному давлению на её вертикальную проекцию.
Вертикальная составляющая равна:
dРв = dР sin α = p dF sin α Так как Fsin α = dFг — горизонтальная проекция элементарной площади dF, то:dРв = р dFг =γh dFг
Величина hdFг есть элементарный объем dVцилиндра, имеющего высоту h и основание dFг.В случае, изображенном на рис. (а), этот объём заполнен жидкостью и вертикальная составляющая dРвнаправлена вниз. В случае, показанном на рис. (б), объем dV не заполнен жидкостью, поэтому его можно назвать фиктивнымэлементарным объёмом. В этом случае составляющая dРвнаправлена вверх. Выражение для dРв представим в виде:
dРв = γ dV откуд Рв = γ V (2)
где V = bFАBC;FАBC —площадь треугольника, у которого одна сторона АВкриволинейная.
Объем Vназывают телом давления.
Из формулы (2) следует: вертикальная составляющая суммарного давления жидкости на цилиндрическую поверхность равна весу жидкости γV в объёме тела давления.
В зависимости от ориентации поверхности тело давления может быть действительным (положительным) и фиктивным (отрицательным).
В случае действительного тела давления (а) вертикальная составляющая Рв направлена вниз, а в случае фиктивного тела давления — вверх (рис. б). Суммарное давление равно: 
Сила Рг проходит через точку, расположенную на расстоянии 2 /3 глубины воды от свободной поверхности.
Сила Рвпроходит через центр тяжести треугольника АВС, который находят с помощью криволинейных медиан. Равнодействующая Р пройдёт через точку пересечения направления действия сил Рг и Рвпод углом β к горизонтальной поверхности, где:tg β = Рв / Рг
21. Толщина стенки цилиндрической трубы, находящейся под избыточным давления.
Рассмотрим вопрос о нахождении допускаемого давления жидкости в трубе круглого сечения.
Мысленно разделив трубу на две части вертикальной (диаметральной) плоскостью, запишем, как определяется сила избыточного давления жидкости на одну половину трубы длиной L:
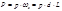
Эта сила уравновешивается двумя силами, приложенными к стенкам трубы в местах условного разреза, каждая из которых находится как: 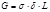
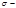
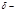

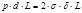
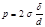
Если напряжение в стенках трубы будет равно предельно- допускаемому, то допускаемое давление в трубе: 
Для заданного избыточного давления в трубопроводе и материале трубы, можно найти толщину стенки трубы: 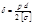

22. Плавучесть и остойчивость плавающих тел.
S
Если бы это равенство не соблюдалось, то тело бы начало двигаться.
Верт. Силы давления BAD и BCD- силы тяжести тел давления опираются на эти поверхности.
Результирующая сила:

Если G>P-тело тонет и наоборот.
При всплытии объем вытесненный телом воды меняется от W до W1. Всплытие прекратится, когда P=G.
Водоизмещение-сила тяжести жидкости в объеме воды погруженной в нее части тела.
Ватерлиния-линия ∩свободной поверхности жидк с боковой поверхностью плавающего тела.
При плавании тело может отклоняться по сторонам. Остойчивость-способность тела восстанавливать первоначальное положение.
Условия остойчивости: Лиия действия силы Р ∩ ось плавания в точке М, называется метацентром.
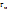
P и G обр пару сил. Если метацентр ниже центра тяжести →тело опрокидывается(неостойчивое плавание)
Метацентрический радиус: 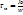
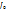
23. Понятие об установившемся и неустановившемся движении жидкости. Неустановившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения т.е.:
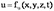
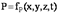
Примером неустановившегося движения может являться вытекание жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде постепенно меняется (уменьшается) по мере вытекания жидкости.
Установившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. u и P зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения:

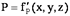
и, следовательно, 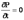
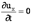
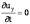
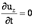
24.Линия тока и элементарная струйка.
Геометрические представления о движении жидкости можно получить с помощью выкторных линий, назыв линиями тока.
Линия тока-линия в каждой точке которой в данный момент времени соответ-ет определ система линий тока, вид расположение которых характеризует поле скоростей.
В турбулентном режиме линии тока имеют расхождения. При установившемся движении значения и направления скоростей не изменяются во времени и линии тока совпадают с траекториями движения частиц жидкости.Линии тока не могут пересекаться. Они дают фотографический снимок с картин распр-я в жидкости векторов.
Поверхность, образ-я линиями тока, проведенными через все точки какой-либо заданной линии наз поверхностью тока.
Часть движ-ия жидкости,огр поверхностью тока, подведенной в данное мгновение черз все точки бескнонечно малого замкнутого контура,наход-я в обл,занятой жидкостью, наз элеметарной струйкой.
через боковую поверхность элементарной струйки жидкость не перетекает. В каждой точке поверхности скорости напр-ия по нормалям и в пределах этой бесконечно малой поверхности принимает одинаковые значения.
Живые сечения струйки(элементарной) –ее нормальное(поперечное) сечение.
Площадь живого сечения может изменятся по длине струйки.
25.Поток жидкости, расход и средняя скорость потока.
Ввиду 2 /2g.
Связь между скоростью ии высотой hииспользована для конструирования приборов, позволяющих измерять скорости течения жидкости, а также и воздуха, или же скорости движения тела в воде или воздухе.
Такие приборы называют гидрометрическими, или напорными, трубками.
Простейшая гидрометрическая трубка 1 (см. рис. 3.5) неудобна в работе, так как отсчет hи приходится делать в непосредственной близости от воды. Этот недостаток устраняется, если соединить в один прибор трубки напорную (динамическую) 2 и пьезометрическую (статическую) 4.
Плоскость нижнего среза статической трубки параллельна направлению скорости.
Если понизить давление в обеих трубках отсосом воздуха через трубку 3, оба уровня поднимутся, но hипри этом не. изменится.
Зная hи, легко подсчитать скорость: 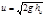
— трубка Пито — напорная трубка Г — образной формы, открытый конец которой, имеющий обтекаемую форму, воспринимает полное давление.
Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения покоя жидкости
Читайте также:
|
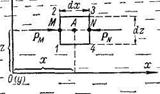 |
1. Силы, действующие на параллелепипед 1—2—3—4:
а) объемная сила равна
где (dx dy dz)ρ — масса жидкости, образующей параллелепипед 1—2—3—4; проекция этой силы на Ох равна:
| Рис. 6. |
б) поверхностные силы: проекция на ось Ох разности сил давления на грани 1—4 и 2—3 равна нулю; проекция на Ох разности сил давления на грани 1—2 и 3—4 равна:
Рм — Р n — Рм (dz dy) — pN (dz dy) = (Р — ½ dx 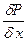
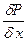
2. Сумма проекций всех сил на ось Ох равна:
фх (dx dy dz)ρ — 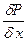
Так выглядит первое уравнение; остальные два пишем по аналогии с первым. Найденные три дифференциальных уравнения (отнесенные к единице массы жидкости) имеют окончательный вид:


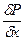
Фy — 
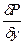
Фz — 

Эти уравнения были получены Л. Эйлером в 1755г.
Дата добавления: 2015-04-18 ; просмотров: 14 ; Нарушение авторских прав
🎦 Видео
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Теорема Эйлера о движении жидкостиСкачать

Решение задачи по гидравлике (механике жидкости) - давление в точкеСкачать

Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

1. Что такое дифференциальное уравнение?Скачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Дифференциальные уравнения. 11 класс.Скачать

Уравнение ЭйлераСкачать

Дифференциальные уравнения 1. Вязкое торможениеСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

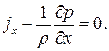

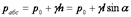
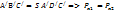
 Pм = Р — ½ dx
Pм = Р — ½ dx