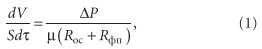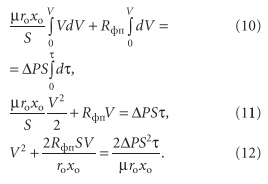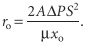Фильтрование воды, а особенно доведение воды до питьевого качества — задача сложная и интересная. Достаточно часто специалисты в области водоподготовки рассчитывают те или иные фильтрационные установки не с помощью формул, а используя эмпирические коэффициенты, основанные на усредненных данных.
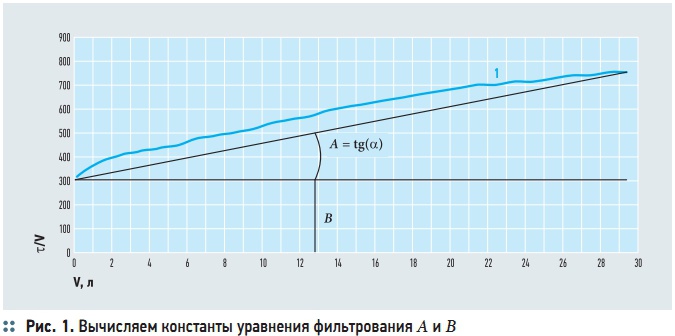
Рис. 1. Вычисляем константы уравнения фильтрования A и В
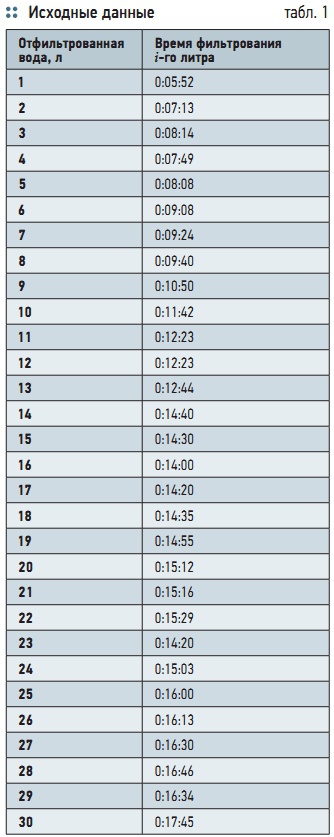
Табл. 1. Исходные данные
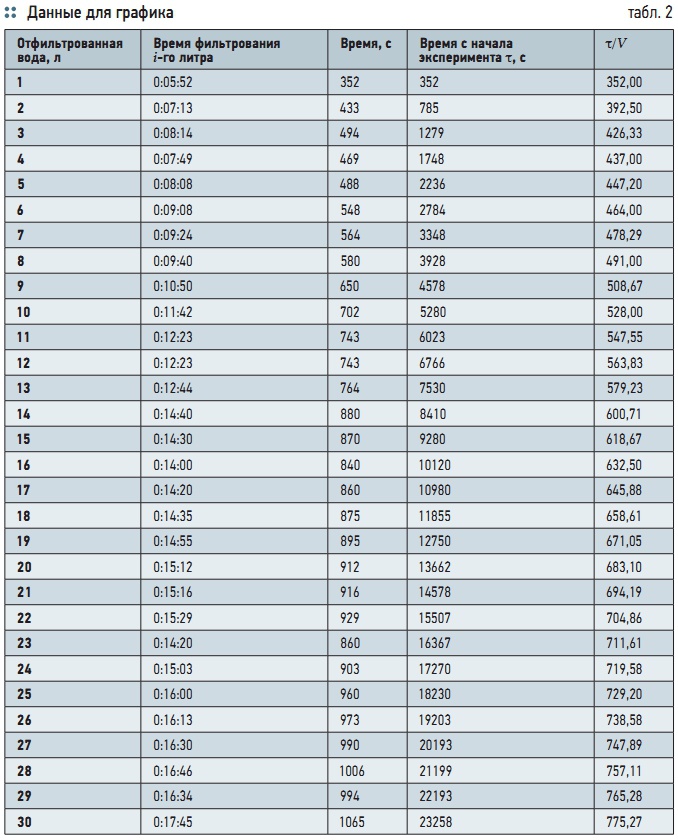
Табл. 2. Данные для графика
Введение
Однако не стоит забывать, что для действительно тщательного и правильного выбора систем фильтрации необходимо воспользоваться соответствующими формулами, грамотно рассчитать все коэффициенты и константы, характерные для данной ситуации. Кроме того, нужно проверить свои расчеты на образце планируемой к очистке воды. Как известно, фильтрование представляет собой процесс отделения твердых веществ от жидкости, происходящий при разности давлений над фильтрующей средой и под ней.
Разность давлений по обе стороны фильтрованной перегородки создают разными способами. В рассматриваемом случае [1] под фильтрованной перегородкой непрерывно создается вакуум, так что процесс фильтрования происходит при постоянной разности давлений. При этом скорость процесса уменьшается в связи с увеличением сопротивления слоя осадка возрастающей толщины. Основное уравнение любого процесса базируется на принципе движущей силы.
В данном случае движущей силой будет являться разница давлений над и под фильтрующей перегородкой. Основной характеристикой процесса фильтрации является ее скорость. Скорость фильтрования определяется как количество жидкости, отфильтрованной за единицу времени через единицу поверхности и зависит от многих параметров: разности давлений, параметров исходной воды, типа перегородки. Все это учитывается в основном уравнении фильтрования.
Данная статья посвящена поиску констант для расчета сетчатых фильтров и мембран микрофильтрации по основному уравнению фильтрования.
Основное уравнение фильтрования
Основное уравнение фильтрования:
где V — количество фильтрата; S — поверхность фильтра; τ — время фильтрации; Δp — разница давлений, движущая сила процесса; μ — вязкость фильтрата; Rос — сопротивление слоя осадка; Rфп — сопротивление фильтровальной перегородки (считаем его величиной постоянной). Cопротивление слоя осадка:Roc = rohoc, (2)где ro — удельное объемное сопротивление слоя осадка (1/м2), т.е. сопротивление, оказываемое потоку жидкой фазы слоем осадка толщиной 1 м.
Для того, чтобы произвести расчет процесса с помощью основного уравнения фильтрования, нам необходимо знать Rос и Rфп, т.к. остальные данные обычно известны. Поскольку слой осадка hос — величина постоянно меняющаяся, для расчета Rос необходимо установить удельное сопротивление ro. Таким образом, задача сводится к вычислению ro и Rфп. Для этого проведем некоторые видоизменения уравнения (1).
Cопротивление слоя осадка
Мы рассматриваем постоянный состав фильтрата, поэтому количество осадка пропорционально объему фильтрата:
Интегрируем основное фильтрования
В связи с тем, что в общем случае в процессе фильтрования значения разности давлений и гидравлического сопротивления осадка с течением времени изменяются, переменную «скорость фильтрования» или «интенсивность» выражают в дифференциальной форме. Так как основное уравнение фильтрования имеет дифференциальный вид, т.е. описывает мгновенную скорость (объем воды, прошедший через единицу площади за единицу времени), а нас интересует получение зависимости для всего процесса в целом, необходимо проинтегрировать это уравнение. Для того, чтобы проинтегрировать уравнение (1), произведем следующие действия:
μdVRос + μdVRфп = ΔpSdt. (8)
Подставим уравнение (7) в уравнение (8), получим:
μdV(rоxоV) + μdVRфп = ΔpSdt. (9)
Проинтегрируем уравнение (9):
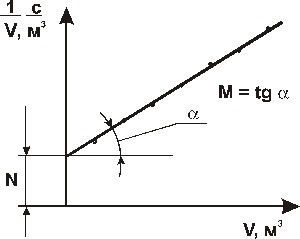
Строим график τ/V
Безусловно, существует несколько способов расчета Rфп и rо. В данной статье нам бы хотелось остановиться на наиболее интересном, геометрическом методе, основанном на построении графика зависимости времени, затраченного на фильтрование каждого следующего литра воды, от объема этой воды. Для того, чтобы найти Rфп и rо, необходимо полу чить зависимость τ/V. Для этого разделим уравнение (12) на дробь:
По экспериментальным данным построим график зависимости τ/V от V. Для этого воспользуемся исходными данными, которые были получены при фильтровании воды с содержанием железа 11,2 мг/л на установке фильтрования с использованием трековой мембраны, которые были получены в материале [1]. Исходные данные приведены в табл. 1. Произведем необходимые расчеты, и полученные данные занесем в табл. 2. Полученная зависимость показано на рис. 1 (линия 1).
Вычисляем константы уравнения фильтрования
Теперь найдем А и В (рис. 1). Для того, чтобы вычислить A, необходимо построить прямую, параллельную оси абсцисс OX и найти тангенс угла экспериментальной зависимости 1 и этой прямой. В данном случае А = 3,49.Для того, чтобы вычислить B, необходимо достроить нашу зависимость до пересечения с осью ординат OY и найти величину, которая отсекается на этой оси ординат. В данном случае В = 300.Используем полученные данные для вычисления констант фильтрования. Из уравнения (15):
Подставляя данные, получаем:
Заключение
Зная полученные величины и подставив их в основное уравнение фильтрования, можно рассчитать предельный слой осадка, время работы фильтра, а также другие не менее важные параметры работы фильтрационной установки, что играет решающую роль для правильного выбора фильтрующей установки.
Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Схема процесса фильтрования. Уравнения фильтрования. Расчет скорости фильтрования и производительности фильтров.
Для тонкой очистки газов от частиц и капельной жидкости применяют процесс фильтрования. Фильтрование заключается в пропускании аэрозоля через фильтровальные перегородки, которые допускают прохождение воздуха, но задерживают аэрозольные частицы.
В фильтр поступает загрязненный газ, частицы примесей оседают на входной части волокнистой перегородки (фильтроэлемента) и задерживаются в порах между волокон, образуя на поверхности перегородки слой.
слой примесей фильтроэлемент корпус
При приближении частицы к волокну действует несколько механизмов, которые улавливанию:
Касание. Частица переносится вдоль линии тока газа к нити или волокну (препятствию). Если частица движется мимо препятствия на расстоянии меньше своего радиуса, то она касается препятствия и захватывается.
Инерция. Частица находится на линии тока, следуя которой она прошла бы мимо препятствия, не касаясь его, но под действием инерции частица сходит с первоначальной линии тока. В результате она сталкивается с препятствием. Чем больше частица, тем больше ее инерция, лучше условия для захвата. При обычных скоростях течения в фильтрах этот механизм мало эффективен для частиц диаметром менее микрометра.
Диффузия Частица настолько мала, что ее траектория становится хаотичной из-за броуновского движения. Захват может произойти, если случайное отклонение приводит частицу к волокну. Этот механизм становится наиболее важным, когда размер частиц меньше 0,1 мкм. Электростатическое осаждение. Частица и препятствие имеют заряды противоположных знаков, вследствие чего частица притягивается к препятствию.
Термофорез. Частица смещается к препятствию под действием градиента температуры.
Гравитационное осаждение. Частица смещается с линии тока, проходящей мимо препятствия, к самому препятствию под действием притяжения между частицей и волокном или под действием земного тяготения. Этот эффект очень мал.
Ситовой эффект. Частица задерживается из-за того, что слишком вели-ка, чтобы пройти через данную пору или канал. Возможности осаждения за счет ситового эффекта, особенно при прохождении потока через чистую ткань, ограничены, т. к. в большинстве случаев размеры частиц значительно меньше размеров пор.
При осаждении одиночной частицы на изолированном волокне касание, инерция и диффузия, являются наиболее важными механизмами. Гравитация и термофорез обычно несущественны, электрические силы могут играть и незначительную роль и очень важную.
Ситовой эффект не используется.
В случае тканевых фильтров значительная часть процесса улавливания протекает в слое осадка частиц на лобовой поверхности фильтра. Обычные механизмы — касание, инерция и диффузия — действуют лишь в течение небольшой части всего цикла фильтрации. Как только после очистки фильтра образуется новой слой осадка, доминирующим механизмом становится ситовой эффект.
Размер частиц играет важное значение при зацеплении и захвате частиц за счет касания ими поверхности облекаемого тела.
Эффект зацепления характеризуется параметром R, который представляет собой отношение диаметров частицы и обтекаемого тела: R=dч/dт
При потенциальном обтекании шара эффективность механизма зацепления находится в пределах R3. R2, а при потенциальном обтекании цилиндра R. R2
Фильтрование применяют для выделения из сточных вод тонкодисперсных твердых или жидких веществ. Разделение проводят при помощи пористых или зернистых перегородок, пропускающих жидкость, и задерживающих диспергированную фазу. Процесс идет под действием гидростатического давления столба жидкости, повышенного давления над перегородкой или вакуума после перегородки.
Выбор перегородок зависит от свойств сточной воды, температуры, давления фильтрования и конструкции фильтра. В качестве перегородок используют металлические перфорированные листы и сетки, тканевые перегородки из природного, искусственного и синтетического волокна. Фильтрованные перегородки должны обладать минимальным гидравлическим сопротивлением, механической прочностью и гибкостью, химической стойкостью, они не должны набухать и разрушаться при заданных условиях фильтрования.
Разность давлений по обе стороны фильтрованной перегородки создают разными способами. Если пространство над суспензией сообщают с источником сжатого газа или пространство под фильтрованной перегородкой при-оединяют к источнику вакуума, то происходит процесс фильтрования при постоянной разности давлений. При этом скорость процесса уменьшается в связи с увеличением сопротивления слоя осадка возрастающей толщины.
Если суспензию подают на фильтр поршневым насосом с постоянной производительностью, то осуществляется процесс фильтрования при постоянной скорости; при этом разность давлений увеличивается вследствие увеличения сопротивления слоя осадка возрастающей толщины.
Если суспензию подают на фильтр центробежным насосом, производительность которого уменьшается при возрастании сопротивления осадка, что обуславливает повышение разности давлений, то производится процесс фильтрования при переменных разности давлений и скорости- Фильтрование производят при следующих разностях давлений:
под вакуумом — 5·10 4 . 9·10 4 Па;
под давлением сжатого воздуха — не более 3·10 5 Па;
при подаче поршневым или центробежным насосом — до 5·10 5 Па;
под гидростатическим давлением — до 5·10 4 Па.
Процесс фильтрования проводят с образованием осадка на поверхности фильтрующей перегородки или с закупоркой пор фильтрующей перегородки.
Фильтрование с образованием осадка наблюдается при достаточно высокой концентрации твердой фазы в суспензии (более 1% объемн )
Фильтрование с закупориванием пор фильтрующей перегородки называют осветлением, оно происходит при концентрации твердой фазы менее 0,7 объемн.%
При разделении суспензий с небольшой концентрацией тонкодисперсированной твердой фазы часто применяют фильтровальные вспомогательные вещества препятствующие прониканию твердых частиц в поры фильтровальной перегородки. В качестве вспомогательных веществ используют тонкодисперсные или тонковолокнистые материалы: диатомит, перлит, асбест, целлюлозу, активированный уголь, древесную муку. При добавлении вспомогательного вещества к разделяемой суспензии концентрация твердых частиц в ней увеличивается, что предотвращает закупоривание пор фильтрующей перегородки.
Фильтрование протекает в ламинарном режиме вследствие небольшого размера пор в слое осадка и фильтровальной перегородки, а также малой скорости движения жидкой фазы в порах. Скорость фильтрования в общем случае выражают в дифференциальной форме:
где V— объем фильтрата, м 3 ; S — поверхность фильтрования, м 2 ; τ – продолжительность фильтрования, с.
Скорость фильтрования прямо пропорциональна разности давлений, но обратно пропорциональна вязкости жидкой фазы и общему гидравлическому сопротивлению слою осадка и фильтрующей перегородки:
dV/(S·dτ) = ΔР/[μ0(Rос+Rфп)], где ΔР – разность давлений, Па; μ0 — вязкость жидкой фазы суспензии, Па*с; Roc— сопротивление слоя осадка, м- 1 ; Rфп — сопротивление фильтрующей перегородки м- 1 .
Объем осадка можно выразить через высоту слоя осадка hoc, а также через отношение объема осадка к объему фильтрата Х0.
hoc·S = x0V откуда толщина осадка составит
hoc=x0V/S Сопротивление слоя осадка равно
Roc= r · hoc =r0— x0 V/S , где r0 удельное объемное сопротивление осадка, м -2 .
С учетом этого выражения основное дифференциальное уравнение фильтрования имеет вид: dV/S·dτ=ΔP/ μо(r0·x0·V/S+Rфп)=wф
При прочих равных условиях скорость фильтрования тем больше и производительность фильтра тем выше, чем меньше объем полученного фильтрата или пропорциональная этому объему толщина слоя осадка на фильтрующей перегородке. Поэтому для повышения производительности фильтра необходимо стремиться к возможно быстрому удалению осадка с фильтрующей перегородки.
Для наибольшей производительности фильтров периодического действия целесообразно как можно чаще повторять циклы его работы, подавая на фильтр небольшие порции суспензии. Однако частое повторение циклов работы фильтра по основным операциям, включающим само фильтрование, промывку и продувку осадка, влечет за собой столь же частое повторение вспомогательных операций загрузки суспензии и удаления осадка. В каждом случае существует оптимальная продолжительность цикла работы фильтра, при которой фильтр обладает наибольшей производительностью.
При значительном сопротивлении фильтрующей перегородки наибольшая производительность периодически действующего фильтра достигается при τосн>τвсп. Τосн=τвсп+2 • корень из μ0 *Rфп 2 /2·ΔР·r0. Экономически оптимальная продолжительность цикла фильтрования достигается при соотношении τ0=(4. 6)τвсп
Это соотношение справедливо при ΔР = const и Rфп= 0.
Видео:1. Что такое дифференциальное уравнение?Скачать

Расчет аппаратов для фильтрования
Уравнения фильтрования. В первом приближении движение жидкости через слой осадка и фильтровальную перегородку можно рассмотреть как движение через слой зернистого материала. Тогда с учетом (5.231), (5.235), (5.241)
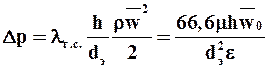
Общий перепад давлений складывается из перепада давлений на слое осадка и фильтровальной перегородки:
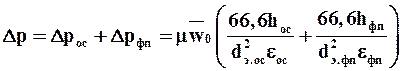
откуда можно получить значение для 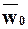
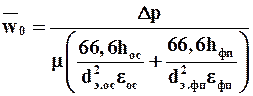
Величина 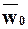
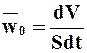
и дифференциальное уравнение фильтрования записывается в виде
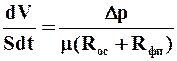
где V – объем фильтрата, м3; S – поверхность фильтрования, м2;t – продолжительность фильтрования, с; 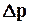
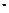
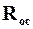
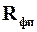
Для интегрирования уравнения (9.20) необходимо установить зависимость между сопротивлением слоя осадка и объемом полученного фильтрата. Учитывая пропорциональность объема осадка и фильтрата, обозначим x0 отношение объема осадка к объему фильтрата. Тогда объем осадка будет равен x0V. Объем осадка может быть выражен произведением 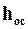
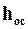
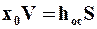
откуда высота равномерного слоя осадка на фильтровальной перегородке составит
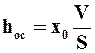
Сопротивление слоя осадка можно выразить равенством
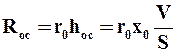
где r0 – удельное объемное сопротивление слоя осадка, м-2.
Подставив 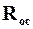
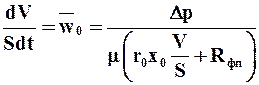
Допускаем, что сопротивлением фильтровальной перегородки можно пренебречь ( 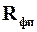
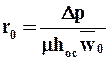
Таким образом удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы жидкость с вязкостью 1 Па×с фильтровалась со скоростью 1 м/с сквозь осадок высотой 1 м.
ПринявV = 0, что соответствует началу фильтрования, когда на фильтровальной перегородке еще не образовался осадок, из уравнения (9.23) получаем
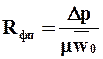
Уравнение фильтрования при постоянной разности давлений. При Dр = const и неизменной температуре для фильтра данной конструкции и известной фильтровальной перегородки все входящие в уравнение (9.23) величины, за исключением V и t, постоянны. Интегрируем это уравнение в пределах от 0 до Vи от 0 до t:
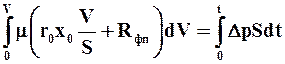
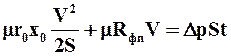
Разделив обе части последнего уравнения на 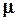
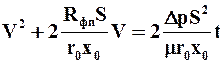
Уравнение (9.26) применимо к несжимаемым и сжимаемым осадкам, поскольку при Dр = const величины r0 и x0 тоже постоянны. Из уравнения (9.23) следует, что при Dр = const по мере увеличения объема фильтрата, а следовательно, и продолжительности фильтрования скорость фильтрования уменьшается.
Уравнения фильтрования при постоянной скорости процесса. При постоянной скорости фильтрования производную dV/dt можно заменить отношением конечных величин V/t. После такой замены, решая уравнение (9.23) относительно Dр, находим
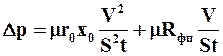
Умножив и разделив первое слагаемое правой части этого уравнения наt и приняв во внимание, что постоянная скорость фильтрования
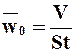
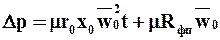
Уравнение (9.29) показывает, что при 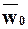
Это уравнение применимо к несжимаемым осадкам; при использовании его для сжимаемых осадков следует иметь в виду зависимость удельного сопротивления осадка от разности давлений.
Уравнение фильтрования при постоянных разности давлений и скорости. Такой вид фильтрования осуществим, когда чистая жидкость движется сквозь слой осадка неизменной толщины при постоянной разности давлений. Движение чистой жидкости в пористой среде называется фильтрацией. Промывку осадка на фильтре способом вытеснения, когда над осадком имеется слой промывной жидкости, можно рассматривать как фильтрацию промывной жидкости сквозь слой осадка постоянной толщины при постоянных разности давлений и скорости.
Приняв в уравнении (9.23) в соответствии с равенством (9.21) вместо x0V/S эквивалентную этому выражению толщину слоя осадка на перегородке 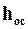
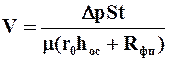
Поскольку Dр = const уравнение (9.30) применимо для несжимаемых и сжимаемых осадков.
Определение постоянных в уравнениях фильтрования. Под постоянными в уравнениях (9.26), (9.28) и (9.30) понимают r0 , x0и 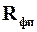
Преобразуем уравнение (9.26) к виду
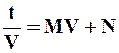
где 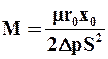
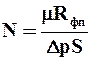
При постоянных температуре и разности давлений все величины, входящие в правые части равенств (9.32) и (9.33), постоянны. Поэтому значения M и N также постоянны, и уравнение (9.31) является уравнением прямой линии, наклоненной к оси абсцисс под углом, тангенс которого М, и отсекающей на оси ординат отрезок N. Для построения указанной прямой в координатах V – t/V наносят ряд точек на основании измеренных в опыте и соответствующих одно другому значений V и t/V (рис. 9.20).
Рис. 9.20. К определению M и N в уравнении фильтрования
Затем по графику определяют величины M и N, после чего из равенств (9.32) и (9.33) вычисляют r0 и 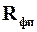
Для несжимаемых осадков, размер частиц которых достаточно велик (порядка 1мм и более), процесс фильтрования можно рассматривать как течение жидкости через зернистый слой. В этом случае величину r0 с учетом уравнений (9.19а) и (9.24) можно определить по зависимости
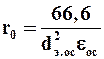
Центробежное фильтрование. Для периодически действующей фильтрующей центрифуги можно выделить три периода: образование осадка, уплотнение осадка и его механическая сушка (отжим). В течение первого периода на поверхности фильтровальной перегородки образуется слой осадка, состоящий из твердых дисперсных частиц, толщина слоя увеличивается до тех пор, пока все элементы дисперсной фазы не перейдут из суспензии в осадок и внутренний радиус слоя суспензии Rc не сравняется с внутренним радиусом осадка Rо. В ходе второго периода происходит уплотнение осадка путем выдавливания жидкости. Третий период характеризуется замещением жидкости в порах осадка газовой фазой, что позволяет получать в процессе центробежного фильтрования менее влажные осадки, чем в осадительных центрифугах.
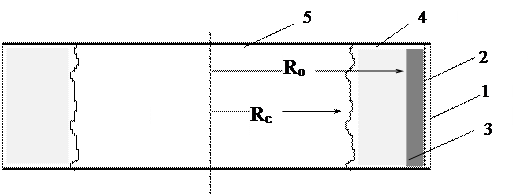 |
Рис. 9.21. Схема барабана фильтрующей центрифуги:
1 – перфорированная стенка; 2 – фильтровальная перегородка; 3 – осадок; 4 – суспензия; 5 – газовая фаза
Движущей силой в первом периоде фильтрования является в основном разность давлений на внутренней поверхности осадка и на внешней поверхности фильтровальной перегородки. Пренебрегаем влиянием сил тяжести при больших значениях фактора разделения Kp (9.9) в центрифугах. Тогда из (6.23) можно показать, что давление на внутренний слой осадка р0 будет равно
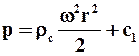
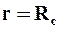
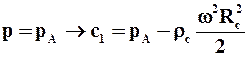
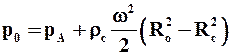
или 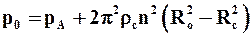
где рА – давление в газовой фазе внутри барабана. Учитывая, что давление на внешней поверхности фильтровальной перегородки также равно рА, которое, как правило, равно атмосферному, получим движущую силу процесса центробежного фильтрования в первом периоде:
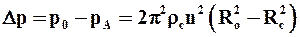
Найденный перепад давлений можно подставить в уравнения (9.20) или (9.23).
В промышленных фильтрующих центрифугах значениеDр достигает 1 – 1,5 МПа. При таких высоких давлениях сжимаемые осадки сильно уплотняются и их гидравлическое сопротивление становится очень большим. Поэтому суспензии, образующие сжимаемые осадки, не рекомендуется разделять на фильтрующих центрифугах. Во втором и в третьем периодах жидкость удаляется из осадка за счет центробежных сил. Описание кинетики при этом имеет сложный характер. Продолжительность центробежного фильтрования в большинстве случаев определяют на базе экспериментальных данных.
Определение производительности фильтров и продолжи-тельности процессов фильтрования. Расчет периодических фильтров сводится к определению производительности фильтра с известной поверхностью фильтрования либо к определению количества фильтров с выбранной поверхностью фильтрования, обеспечивающей заданную производительность.
Производительность одного фильтра, работающего при Dр = const, определяется следующим образом. Время фильтрования t находится из уравнения (9.26):
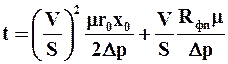
С учетом (9.21) 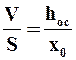
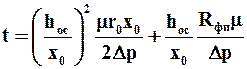
По формуле (9.40) можно определить время (продолжительность) фильтрования, если задана высота слоя осадка, которая зависит от конструкции фильтра и других факторов. Константы фильтрования определяются экспериментальным путем. Время (продолжительность) промывки осадка определяется исходя из уравнения (9.30):
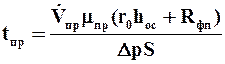
где 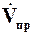
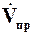
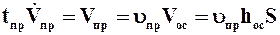
где 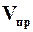
Обозначим через tв.о. продолжительность других вспомогательных операций (сушка осадка, загрузка фильтра, выгрузка осадка и др.) Общая продолжительно работы, учитывающая продолжительность всех осуществляемых операций, будет
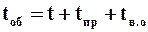
С учетом времени tоб средняя производительность по фильтрату равна
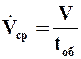
где V определяется по уравнению (9.21), 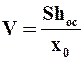
При заданной суточной производительности фильтровальной установки Vуст число циклов фильтрования на одном фильтре kц, которое необходимо осуществить для обеспечения суточной производительности Vуст , будет
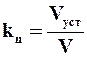
Число циклов фильтрования k1, которое можно провести на одном фильтре в сутки:
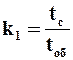
где tс –рабочая продолжительность суток. Уравнения (9.45) и (9.46) позволяют определить необходимое число фильтров N:
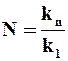
Расчет барабанного вакуум-фильтра непрерывного действия ведется с учетом стандартного распределения поверхности фильтра на технологические зоны. В начале расчета задаются значения: углов сектора (зоны) предварительной сушки осадка, осуществляемой на выходе из зоны фильтрования (jс1); зоны съема осадка j0; зоны регенерации фильтровальной перегородки jр и мертвых зон jм1, jм2, jм3, jм4, (находящихся между технологическими зонами), в которых ячейки отключены от источников вакуума и сжатого газа. Ориентировочную частоту вращения барабана, обеспечивающую образование осадка заданной толщины (фильтрование), его промывку и сушку, определяют по уравнению
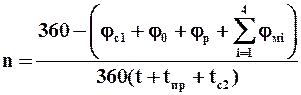
где t, tпр, tс2 – соответственно время фильтрования, промывки и сушки осадка после промывки.
Время (продолжительность) фильтрования определяется по уравнению (9.40), а время промывки осадка – по уравнению (9.41), при этом удельный объем промывной жидкости должен быть предварительно экспериментально определен. Продолжительность сушки осадка после промывки задается также из экспериментальных данных.
Время полного цикла работы фильтра tц представляет величину, обратную частоте вращения барабана 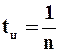
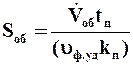
где 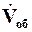
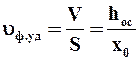
По найденному значению Sоб по каталогу выбирают типоразмер фильтра и определяют число фильтров. Затем проверяют пригодность выбранного фильтра. Устанавливают соответствие рассчитанной частоты вращения барабана диапазону частот, указанному в каталоге; сравнивают рассчитанный и стандартный углы сектора (зоны) фильтрования. Если частота выходит за пределы указанного диапазона или рассчитанный угол фильтрования больше стандартного, следует повторно выполнить расчеты, задавшись другой высотой слоя осадка.
После этого производят уточненный расчет фильтра. Принимают по каталогу данные распределения технологических зон. Частоту вращения барабана выбирают наименьшую из рассчитанных по следующим формулам:
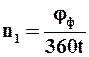
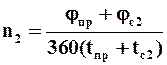
где jф – угол зоны (сектора) фильтрования; jпр – угол сектора промывки; jс2 – угол сектора сушки осадка после промывки.
🔍 Видео
Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Составить дифференциальные уравнения семейств линийСкачать

Основные понятия дифференциальных уравнений от bezbotvyСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Как распознать талантливого математикаСкачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения 1. Вязкое торможениеСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Дифференциальные уравнения 1-го порядка.Скачать

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Эффект Вентури и трубка Пито (видео 16) | Жидкости | ФизикаСкачать

Закон БернуллиСкачать

Уравнение Эйлера - bezbotvyСкачать