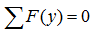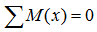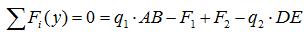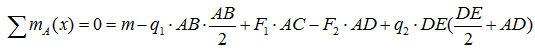Основная форма уравнений равновесия балочной системы

Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.

Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.

При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.

В результате имеем следующие уравнения статики:

1. Сумма проекций всех сил на вертикальную ось равна нулю
   
2. Сумма моментов относительно любой точки системы тоже равна нулю.
   

Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.

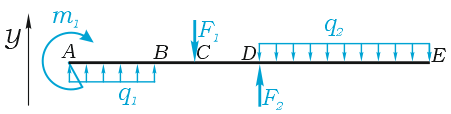
Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A :

Дополнительные материалы

• Порядок определения момента от распределенной нагрузки.
• Правила знаков при составлении уравнений статики для систем находящихся в равновесии.

Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Балочные системы. Определение реакций опор и моментов защемления

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Занятие 6. (2 часа)
Балочные системы. Определение реакций опор и моментов защемления

6.1. Виды нагрузок и разновидности опор
6.1.1. Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные.
Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой
(рис. 6.1).

Рис.6.1. Замена распределенной нагрузки равнодействующей сосредоточенной силой
q — интенсивность нагрузки;
l — длина стержня;
G = ql — равнодействующая распределенной нагрузки.

6.1.2. Разновидности опор балочных систем (см.занятие 1)
Балка — конструктивная деталь в виде прямого бруса, закреп­ленная на опорах и изгибаемая приложенными к ней силами.
Высота сечения балки незначительна по сравнению с длиной.
а) Жесткая заделка (защемление) (рис. 6.2)

Рис.6.2. Жесткая заделка (защемление)
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы RАx и RAy и парой с моментом МR.

Для определения этих неизвестных удобно использовать систему уравнений в виде

Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например В:

б) Шарнирно-подвижная опора (рис. 6.3)
Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

Рис.6.4. Шарнирно-подвижная опора

в) Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.

Рис.6.4. Шарнирно-неподвижная опора

г) Балка на двух шарнирных опорах (рис. 6.5)

Рис.6.5. Балка на двух шарнирных опорах
Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

Составляются уравнения моментов относительно точек крепления балки.

Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.

Для контроля правильности решения используется дополнительное уравнение:

При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):

6.2. Примеры решения задач
Пример 1. Одноопорная (защемленная) балка нагружена сосредоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.

Решение:
1. В заделке может возникнуть реакция, представляемая двумя составляющими (RАу, RАx), и реактивный момент МА. Наносим на схему балки возможные направления реакций.

Замечание.
Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.

В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке.

Для решения удобно использовать систему уравнений равновесия в первой форме.
Каждое уравнение будет содержать одну неизвестную.

Знаки полученных реакций (+), следовательно, направления реакций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Пример 2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 6.8а). Определить реакции опор.

Решение:
1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.
Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.
2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно.
3. Заменяем распределенную нагрузку сосредоточенной:

Сосредоточенную силу помещаем в середине пролета, далее задача решается с сосредоточенными силами (рис. 6.8 б).

4. Наносим возможные реакции в опорах (направление произвольное).
5. Для решения выбираем уравнение равновесия в виде

Занятие 7. (2 часа) Контрольная работа №1

Занятие 8. (2 часа) Пространственная система сил.
Центр тяжести.

8.1. Момент силы относительно оси.
Момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью (рис. 8.1а).
Moo(F) = пр Fα,
α — расстояние от оси до проекции F;
npF — проекция силы на плоскость, перпендикулярную оси ОО.
npF = F cos α; MОО(F) = F cos α ∙ α.
Рис.8.1. Момент силы относительно оси.

Момент считаем положительным, если сила разворачивает тело по часовой стрелке. Смотреть со стороны положительного направления оси.

Если линия действия силы пересекает ось или линия действия силы параллельна оси, моменты силы относительно этой оси равны нулю (рис. 8.1б).

Силы и ось лежат в одной плоскости, они не смогут повернуть тело вокруг этой оси.
F1 пересекает ось; MОО(F1) = 0;
F2||ОО- npF2 = 0; MOO(F2) = 0.

8.2. Пространственная сходящаяся система сил.
а) вектор в пространстве.
В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора образуют ребра прямоугольного параллелепипеда, вектор силы совпадает с диагональю (рис. 8.2).

Рис.8.2. Вектор в пространстве.

Модуль вектора может быть
получен из зависимости

αх, αу, αz — углы между вектором осями координат.

б) Пространственная сходящаяся система сил
Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 8.3),

Рис.8.3. Пространственная сходящаяся система сил.
FΣ = F1 + F2 + F3 + • • • + Fn.
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.

Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и сум­мируем соответствующие проекции
(рис. 8.4).

Рис.8.4. Проекции равнодействующей на оси координат
Получим проекции равнодействующей на оси координат:

в) Произвольная пространственная система сил
Приведение произвольной пространственной системы сил к центру О
Дана пространственная система сил (рис. 8.5а). Приведем ее к центру О.

Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения

Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 8.5в).

Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.
Абсолютное значение главного вектора (рис. 8.56) равно

г) Уравнения равновесия пространственной системы сил
При равновесии Fгл = 0; Мгл = 0.
Получаем шесть уравнений равновесия:

Шесть уравнений равновесия пространственной системы сил соответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей.

8.3. Сила тяжести.
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, прило­женные к частицам твердого тела, образуют систему сил, линии действия которых сходят­ся в центре Земли (рис. 8.8). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.

Рис.8.8. Сила тяжести.

8.4. Точка приложения силы тяжести.
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.9).

Рис.8.9. Тело, составленное из частей, в пространственной системе координат

Тело состоит из частей, силы тяжести которых qk приложены в центрах тяжести (ЦТ) этих частей.

Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре С.
Xc, Yс и Zc — координаты центра тяжести С.
Xk, Yk и Zk — координаты центров тяжести частей тела.

8.4. Центр тяжести однородных плоских тел (плоских фигур)
Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы.
Для плоских тел можно записать:
V = Ah,
где А — площадь фигуры, h — ее высота.
Тогда после подстановки в записанные выше формулы получим:

Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.

8.5. Определение координат центра тяжести плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты.
Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.10) :
а) — круг; б) — квадрат, прямоугольник; в) — треугольник;
г) — полукруг).
Рис.8.10. Определение координат центра тяжести плоских фигур

При решении задач используются следующие методы:
1) метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить;
3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.

Рис.8.12. Составное сечение из листа и прокатных профилей.

Занятие 9. (2 часа)
Основные понятия кинематики

9.1.Основные кинематические параметры
а) Траектория
Линию, которую очерчивает материальная точка при движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой, плоской и пространственной линией.
Уравнение траектории при плоском движении: у = f(x).

б) Пройденный путь
Путь измеряется вдоль траектории в направлении движения. Обозначение — s, единицы измерения — метры.

в) Уравнение движения точки
Уравнение, определяющее положение движущейся точки в зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки,
рассматриваемой как начало отсчета (рис. 9.1).
Такой способ задания движения называется естественным.

Таким образом, уравнение движения можно представить в виде
S = f (t).
Положение точки можно также определить, если известны ее координаты в зависимости от времени
(рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения:

В случае пространственного движения добавляется и третья координата
z = f3(t)
Такой способ задания движения называют координатным.

г) Скорость движения
Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.
Скорость — вектор, в любой момент направленный по касательной к траектории в сторону направления движения (рис. 9.3).
Если точка за равные проме­жутки времени проходит равные расстояния, то движение называют равномерным.
Рис.9.3. Скорость движения.

Средняя скорость на пути AS определяется как

где ΔS — пройденный путь за время Δt;
Δt — промежуток времени.
Если точка за равные промежутки времени проходит неравные «пути, то движение называют неравномерным.
В этом случае скорость — величина переменная и зависит от времени v = f(t).
При рассмотрении малых промежутков времени (Δt → 0) средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как производную по времени:

За единицу скорости принимают 1м/с. Иногда скорость измеряют в км/ч,

д) Ускорение точки
Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.
Скорость точки при перемещении из точки M1 в точку М2 меняется по величине и направлению. Среднее значение ускорения за этот промежуток времени (см. рис. 9.4.)

Рис.9.4. Ускорение точки.

При рассмотрении бесконечно малого промежутка времени среднее ускорение превратится в ускорение в данный момент:
Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное (рис. 9.5).
Нормальное ускорение αn характеризует изменение скорости по направлению и определяется как →
где r — радиус кривизны траектории в данный момент времени.

Касательное ускорение αt характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости.
Формула для определения касательного ускорения имеет вид:

Значение полного ускорения определяется как: (см. рис. 9.6).
Рис.9.6. Определение полного ускорения

Курс повышения квалификации

Охрана труда

• Сейчас обучается 112 человек из 42 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 350 человек из 63 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 231 человек из 54 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 573 749 материалов в базе

Другие материалы

• 26.12.2020
• 447
• 5

• 15.12.2020
• 208
• 0

• 14.12.2020
• 193
• 0

• 26.10.2020
• 977
• 16

• 25.10.2020
• 303
• 4

• 24.10.2020
• 138
• 1

• 15.10.2020
• 77
• 0

• 02.10.2020
• 94
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 18.05.2020 978
• PPTX 2.1 мбайт
• 7 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Булдакова Светлана Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 21900
• Всего материалов: 238

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Сопромат для чайников, основные расчетные формулы

Итак, давайте разбираться, зачем понадобилось ломать школьную линейку, оставляя детей без школьных принадлежностей, и чем это может нам помочь. Пришло время добавить к наглядности несколько формул, тут все будет почти так же просто и понятно, как и в первой части сопромата для чайников, но понадобятся знания математики на уровне 4-5 классов и начальные знания по геометрии.

4. Реакции опор.

Мы выяснили, впрочем, это и без нас было известно, что у всего есть предел. За пределом у человека — смерть, у строительной конструкции — разрушение, но за жизнь сражаются все. Когда мы давили на линейку пальцем в одном из мест, где линейка опиралась на книги, победить линейку нам не удалось и мы своим пальцем чувствовали, как линейка упиралась, но не прогнулась ни на миллиметр. Причем, чем сильнее мы давили на линейку, тем сильнее она упиралась, при этом сила, с которой мы давили на линейку была сравнима с силой отпора.

В реальном мире все очень сложно — любое вещество, даже очень простое, устроено очень непонятно. Одни вещества состоят из атомов, соединенных в кристаллическую решетку, при этом материал может быть монокристаллическим или поликристаллическим. В других веществах атомы входят в состав молекул, которые могут быть и простыми и очень сложными. Но между всеми этими атомами или молекулами существует строгая связь. Все эти атомы и молекулы держатся на определенном природой расстоянии и когда мы давим пальцем на линейку, то мы пытаемся уменьшить расстояние между атомами или молекулами, а молекулы да атомы этого не хотят и сопротивляются, говоря научным языком возникает напряжение, т.е. расстояние между атомами или молекулами уменьшается, но если палец убрать, то атомы и молекулы вернутся на свои места.

Мало того, когда мы давим на линейку, деформации возникают не только в веществе линейки, но и книги, в том месте где на книгу опирается линейка , в веществе стола, на котором лежат книги и так далее, до самого земного ядра. Кстати говоря, для некоторых веществ термин напряжение можно понимать буквально — этот эффект положен в основу работы пьезоэлементов, но не будем отвлекаться. Так вот когда мы давим пальцем на линейку в точке опоры, то часть энергии переходит в упругие деформации, часть в неупругие деформации, часть в нагрев вещества, еще какая-то часть в звуковые колебания и так далее, одним словом процесс сложный, но вот за что я люблю строительную механику, так это за то, что в строймехе все просто, потому как строительная механика придумана не для того, чтобы усложнять нам жизнь, а чтобы жизнь и, в частности, расчет строительных конструкций, упрощать.

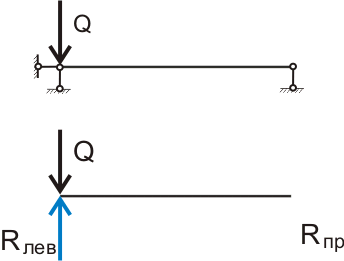
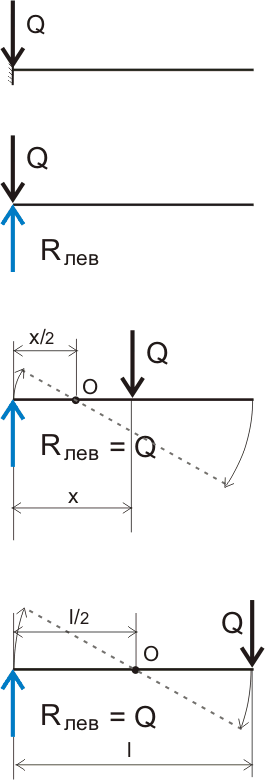
В строительной механике этот сложный комплекс событий называется реакцией опоры. Считается, что когда мы прикладываем силу (сосредоточенную нагрузку) на опоре (см. рис.4.1), то возникает реакция опоры, численно равная приложенной нагрузке и направленная противоположно — красота! Таким образом, если мы приложили на опоре нагрузку 1 Ньютон, то на опоре возникает реакция тоже 1 Ньютон, при этом на второй опоре никакой нагрузки нет, поэтому и реакция опоры равна 0. Такое допущение позволяет заменить опоры, точнее опорные связи, реактивными силами — реакциями опор. Для простоты восприятия можно измерять силы в килограмм-силах, 1 кгс ≈ 10 Н (если быть более точным, то 1 кгс = 9.81 Н). И теперь, если рассматривать балку висящей в воздухе, то для того, чтобы балка не падала, другими словами находилась в состоянии статического равновесия, достаточно в одной точке приложить к балке две равные по значению, но противоположно направленные силы.

Рисунок 4.1. Замена опорных связей реактивными силами — опорными реакциями.

5. Уравнения статического равновесия (проекции сил).

Вроде все просто, но на самом деле мы воспользовались всеми основными аксиомами статики:

1. При всяком воздействии одного тела на другое тело в другом теле возникает противодействие, равное по значению воздействию, но направленное противоположно. В данном случае противодействие — это реакция опоры.

2. Механическое состояние тела не изменится, если освободить тело от связей и приложить к тем же точкам тела силы, равные действовавшим на них силам реакций связей. В данном случае мы заменили опоры опорными реакциями.

3. Если тело под воздействием системы сил находится в состоянии равновесия (покоя) или продолжает двигаться с постоянной скоростью, то такая система сил, является уравновешенной.

Таким образом мы можем составить первых два уравнения, удовлетворяющие условиям статического равновесия системы:

∑_у = Q — R_лев — R_пр = 0 (5.1) — для сил, действующих вдоль оси у.

∑_х = 0 (5.2) — для сил (которых в данном случае нет), действующих вдоль оси х.

Примечание: так как горизонтальных сил в данном случае нет, то и горизонтальная опорная реакция R H _лев = 0, при замене опорных связей на реактивные силы не показана для упрощения восприятия.

Всех нас в школе учили, что ось х проходит горизонтально, а ось у — вертикально, нарушать эту традицию не будем (хотя принципиального значения это не имеет). Так как реакция на правой опоре равна нулю, то получается, что реакция на левой опоре равна действующей силе, оказывается — это тоже одна из аксиом статики:

4. Две силы, приложенные к некоему телу, считаются уравновешенными тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.

5. Не нарушая равновесного состояния тела, к нему можно приложить или отнять от него любую уравновешенную систему сил.

4.1. Определение опорных реакций.

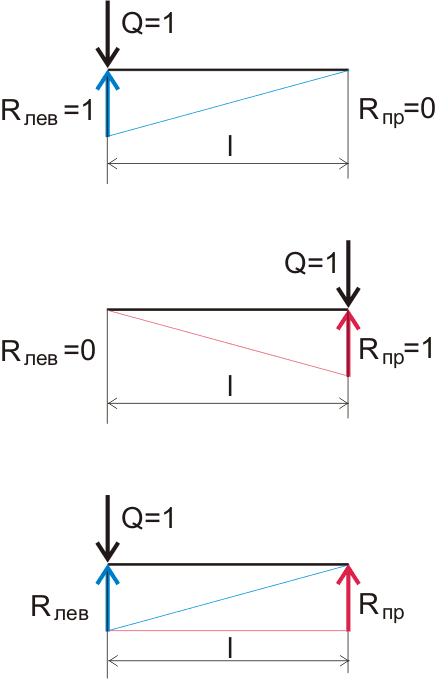
Теперь немного усложним задачу. Наша линейка (то есть балка) лежит на двух опорах и когда мы давим на линейку пальцем между опорами, а говоря по-научному, прикладываем сосредоточенную нагрузку, то реакция возникает на обеих опорах. Так как статическое равновесие системы мы можем наблюдать даже и невооруженным глазом, то логично предположить, что суммарная реакция опор численно равна приложенной нагрузке. Определить значение реакций опор можно простым графическим методом (по линиям влияния):

Рисунок 5.2. Графическое отображение изменения реакций опор в зависимости от расстояния приложения нагрузки.

Если у нас нагрузка Q = 1 кгс приложена на левой опоре, то реакция на левой опоре (на графике обозначена синим цветом) будет R_лев = 1 кгс, а на правой опоре R_пр = 0 кгс. Если соединить эти значения, то мы получим прямоугольный треугольник, у которого нижний катет — это длина балки, второй катет — это реакция на опоре, к которой приложена нагрузка, гипотенуза в данном случае показывает изменение реакции опоры по длине балки, эта линия и называется линией влияния. Если изобразить то же самое для реакции на правой опоре, то мы получим точно такой же треугольник, но для наглядности изобразим его перевернутым. В итоге мы получили обычный прямоугольник из двух прямоугольных треугольников, но на самом деле это магический прямоугольник (номограмма), который без особых расчетов позволяет определить реакцию на любой опоре в зависимости от точки приложения нагрузки:

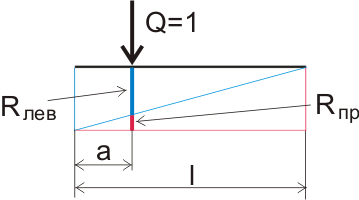
Рисунок 5.3. Графическое определение реакций опор.

Например, расстояние между книгами 20 см. Это значит, что расстояние между опорами (пролет нашей балки) — 20 см, а в общем случае l. Длина балки измеряется по оси х. Если приложить сосредоточенную нагрузку на некотором расстоянии от левой опоры, обозначим его литерой а, то значение реакции левой опоры будет равно длине отрезка, проведенного перпендикулярно длинному катету синего треугольника, а значение реакции правой опоры — это длина отрезка, проведенного перпендикулярно длинному катету красного треугольника. В сумме они составляют единицу, так как мы принимали значение нагрузки равное 1.

Определить реакцию опор можно и математическими формулами, описывающими пропорциональность прямоугольных треугольников: Если нагрузка приложена на расстоянии а от опоры при общей длине балки l, то реакция на правой опоре будет:

R_пр = В = Qа/l (4.1)

а реакция на левой опоре будет:

R_лев = А = Q(l — а)/l (4.2)

Конечно при расчетах все пользуются формулами, но наглядность треугольников нам еще пригодится.

При определении реакции опор от действия распределенной нагрузки, сначала определяется равнодействующая сила, т.е. распределенная нагрузка сводится к сосредоточенной, а потом определяются реакции опор в зависимости от точки приложения сосредоточенной нагрузки. Если распределенная нагрузка является равномерно распределенной и приложена по всей длине балки, то реакции опор будут А = В = ql/2. Как определить реакции опор в других случаях, надеюсь, станет понятно из дальнейшего описания.

6. Уравнения изгибающего момента, третье уравнение статического равновесия системы

Если мы положим 20 см линейку на книги и надавим пальцем посредине, то линейка прогнется на некоторое расстояние, если мы возьмем 40 см линейку такого же сечения и из такого же материала, обопрем ее на книги, уложенные на расстоянии 40 см, и приложим к линейке точно такую же нагрузку, то расстояние, на которое прогнется линейка, будет больше, в чем же дело? ведь ни нагрузка, ни материал балки, ни сечение балки не изменились, изменилась только длина балки.

Строительная механика это чудо объясняет так: силы, действующие на балку, это одно, а вот изгибающий момент, возникающий в рассматриваемом поперечном сечении при действии силы — это совсем другое.

Все мы помним Архимеда и его радость при открытии принципа рычага, так вот этот принцип действует везде, суть его сводится к следующему: чем больше рычаг, тем меньшую силу можно приложить для совершения одной и той же работы.

В теоретической и строительной механике используется понятие плечо силы, как более корректное, таким образом считается, что внутренние напряжения, возникающие в поперечном сечении балки под действием нагрузки, прямо пропорциональны плечу действующей силы. А это значит, что реакции опоры — это силы которые пытаются изогнуть балку, при этом точка опоры рычага — это наша сосредоточенная нагрузка. Такое изменение значения момента в зависимости от плеча силы в математике называется изменением значения функции в зависимости от переменной х, таким образом получается, что значение момента в любой точке нашей балки можно описать уравнением М = Рx. Формула вроде бы не сложная, но очень важная.

Получается, что на участке балки от начала до точки приложения силы Q на балку действует только одна сила — реакция опоры R_лев (для простоты реакции на опорах часто обозначаются большими буквами, так как опор бывает много, крайнюю левую опору принято обозначать — «А«) и тогда уравнение момента на этом участке будет выглядеть:

М = Ах (0≤ х 7. Балка на двух шарнирных опорах.

7.1. Для балки, на которую действует сосредоточенная нагрузка посредине балки, определить изгибающий момент в любой точке поперечного сечения на левом участке балки проще простого: нужно умножить реакцию одной из опор на расстояние от этой опоры до точки приложения нагрузки (на участке балки от х=0 до х= l/2). В математическом выражении это будет выглядеть так:

М=(Q/2)x (7.1)

Так как в данном случае реакция каждой из опор равна половине от действующей нагрузки. Максимальное значение изгибающего момента также будет посредине, т.е. на расстоянии l/2 от начала балки и будет составлять:

M=(Q/2)(l/2) = Ql/4 (7.2)

Полное уравнение моментов, на участке где l/2 2 /8 (7.4)

Вывести данную формулу в общем-то несложно. Распределенная нагрузка рассматривается как очень много сосредоточенных нагрузок, приложенных на одинаковом расстоянии друг от друга. Далее для каждой нагрузки можно построить свою эпюру изгибающих моментов, а потом эти эпюры сложить или сразу строить эпюру, учитывающую действие сосредоточенных нагрузок. Чем больше будет сосредоточенных нагрузок, тем менее ломаным будет низ эпюры. Чтобы каждый раз не рисовать огромное количество эпюр используется интегральное вычисление, для этого его и придумали. Так как у нас на правой или на левой половине балки действуют две силы: реакция опоры и распределенная нагрузка, то значение изгибающего момента в некотором поперечном сечении балки можно определить, решив уравнение:

М = (ql/2)х — (qх)х/2 (7.4.а)

в данном случае значение распределенной нагрузки сначала сводится к сосредоточенной нагрузке, действующей на некотором участке х, а затем умножается на плечо силы х/2. Таким образом посредине балки значение изгибающего момента будет составлять:

М = (ql/2)l/2 — (ql/2)l/(2·2) = ql 2 /4 — ql 2 /8 = ql 2 /8 (7.4.b)

В математике такая операция называется интегрированием уравнения в пределах от 0 до l/2. А это значит, что сосредоточенная нагрузка, действующая на балку, это производная изгибающего момента. Если еще раз посмотреть на построенные нами эпюры, то мы увидим, что, действительно, значение максимального изгибающего момента (посредине балки) равно площади прямоугольника эпюры «Q» (рисунок 7.1) или площади треугольника эпюры «Q» (рисунок 7.2). Кроме того сосредоточенная нагрузка — это производная равномерно распределенной нагрузки и таким образом равномерно распределенная нагрузка — это вторая производная изгибающего момента, а в свою очередь изгибающий момент — это вторая производная от величины прогиба балки (первая производная от величины прогиба — это угол поворота), и, значит, что все эти эпюры сил, моментов, углов поворотов и прогибов конструкции (здесь не приводятся) тесно связаны между собой, но не будем углубляться в теорию, хотя для меня в свое время это было чуть ли не первое наглядное применение совершенно абстрактных в школьную пору интегралов и производных. Вот такая математика.

Пример расчета балки на действие равномерно распределенной нагрузки по всей длине балки приводится отдельно. Если неравномерно распределенная нагрузка действует не по всей длине балки, то вам сюда.

Конечно же, вариантов нагрузок, приложения нагрузок, количества опор, видов опор и, соответственно, вариантов построения эпюр — великое множество (а ведь есть еще и статически неопределимые балки), но для решения простых задач по расчету строительных конструкций в подробном рассмотрении других вариантов нет необходимости, хотя еще один пример все же приведу (для более логичного перехода к следующим положениям сопромата).

8. Консольная балка.

Если взять ту же линейку, один конец линейки всунуть между книгами, а лучше между кирпичами, а второй конец оставить на весу, то мы получим модель консольной балки. Особенность консольной балки в том, что у нее только одна опора, причем жесткое защемление не позволяет балке свободно вращаться вокруг этой опоры. Так как опора только одна, то где бы мы ни приложили нагрузку к балке реакция опоры всегда будет равна приложенной нагрузке. Если мы как и в случае с балкой на шарнирных опорах попробуем убрать опору, заменив ее реакцией, то условие равновесия системы не будет соблюдаться, две равные по значению, противоположно направленные силы, не лежащие на одной прямой, будут вращать балку вокруг некоторой точки «о»:

Рисунок 8.1. Возникновение вращающего момента при приложении равных сил в разных точках.

Как видно из рисунка 8.1 и понятно из описания природы момента, чем больше расстояние между точками приложения сил, тем больше будет вращающий момент. Чтобы соблюсти условие равновесия системы нам необходимо приложить к балке другой вращающий момент, т.е. еще одну пару сил, которая будет пытаться вращать балку в противоположную сторону.

Изгибающий момент, возникающий на жесткой опоре консольной балки при действии сосредоточенной нагрузки:

M = -Qx (8.1)

Изгибающий момент, возникающий на жесткой опоре консольной балки при действии распределенной нагрузки по всей длине балки:

M = -(ql)l/2 = -ql 2 /2 (8.2)

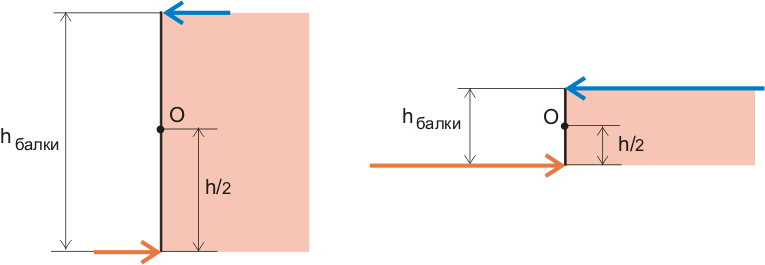
На схеме это можно изобразить с помощью условного обозначения изгибающего момента (известного нам из первой части), но нас сейчас интересует конкретика. Так как балка у нас имеет вполне осязаемые высоту и ширину, то логично было бы приложить эти силы к балке, или, выражаясь более точно, к поперечному сечению балки и тут даже глазом, невооруженным сопроматом, видно, что чем больше высота балки, тем меньшие силы можно прикладывать к самому верху и к самому низу балки, чтобы значение момента было одинаковым:

Рисунок 8.2. Увеличение значения сил при уменьшении высоты балки при одинаковом вращающем моменте.

При этом верхняя сила пытается балку растянуть, а нижняя сила пытается балку сжать. Вроде бы ничего сложного тут нет, все достаточно просто и понятно, но на самом деле мы открыли самую главную тайну сопромата:

Изгибающий момент, действующий на любую строительную конструкцию в некоторой точке, можно рассматривать как пару сил, действующих на поперечное сечение балки в этой точке.

9. Метод сечений

Такой подход позволяет нам при решении задач рассматривать не всю балку, а только ее часть, заменив отсутствующую часть парой сил, действующих на поперечное сечение балки. Так, например, мы могли бы не рассматривать всю балку (рисунок 7.2), а только правую половину, заменив левую половину моментом или парой сил.

А если в рассматриваемом поперечном сечении действуют касательные напряжения, определяемые по эпюре поперечных сил, и(или) нормальные напряжения, определяемые по эпюре нормальных сил, то для того, чтобы отсеченная часть балки находилась в равновесии, мы должны все эти нагрузки приложить к рассматриваемому поперечному сечению.

В этом и состоит суть метода сечений:

• При решении задач мы рассматриваем не всю балку, а только ее часть, отсеченную поперечным сечением.
• Чтобы эта часть оставалась в состоянии статического равновесия, мы должны приложить в рассматриваемом поперечном сечении внешние силы.
• Внутренние напряжения, возникающие в рассматриваемом поперечном сечении — это реакция материала на действие внешних сил.

Таким образом, решая перечисленные выше уравнения, мы определяем значения внешнего изгибающего момента и теперь пришло время узнать, какой же будет на это реакция материала.

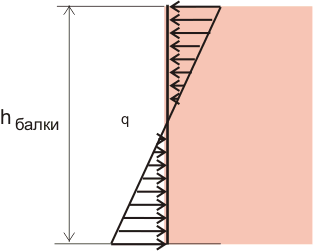
В данном случае мы приложили силы к самому верху и к самому низу балки (рисунок 8.2), но мы можем прикладывать эти силы в любых точках поперечного сечения балки, главное чтобы не изменялось значение внешнего момента. Сосредоточенные силы можно заменить распределенной нагрузкой, которая будет создавать такой же изгибающий момент, причем значение распределенной нагрузки может изменяться в зависимости от высоты балки и графически может быть обозначено так:

Рисунок 8.3. Изменение распределенной нагрузки по высоте балки.

Почему распределение нормальных напряжений по высоте поперечного сечения балки имеет такой странный вид, мы сейчас и узнаем.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Основы строймеха и сопромата . Базовые понятия

Оценка пользователей:9.4 (голосов: 32)Переходов на сайт:185229Комментарии:

Низкий вам поклон за доступно изложенные материалы по сопромату!)
В институте курил бамбук и как-то не до сопромата было, курс выветривался в течение месяца)))
Сейчас работаю архитектором-проектировщиком и постоянно встаю в тупик при необходимости в расчетах, зарываюсь в жиже формул и разных методик и понимаю что упустил азы..
Читая Ваши статьи в голове постепенно наводится порядок — все наглядно и очень доступно!

спасибо вам человек!!))
у мня 1 единственыый вопрос если максимальная нагрузка на 1 м равен 1 кг*м то на 2 метра ?
2 кг*м или 0,5кг*м.

Если имеется в виду распределенная нагрузка на погонный метр, то распределенная нагрузка 1кг/1м равна распределенной нагрузке 2кг/2м, что в итоге все равно дает 1кг/м. А сосредоточенная нагрузка измеряется просто в килограммах или Ньютонах.

Формулы это хорошо! но как и какими формулами расчитать конструкцию для навеса а самое главное какой металл (профильную трубу) размером должен быть.

Если Вы обратили внимание, то данная статья посвящена исключительно теоретической части, а если Вы еще и проявите сообразительность, то без особого труда найдете примера расчета конструкций в соответсвующем разделе сайта: Расчет конструкций. Для этого достаточно перейти на главную страницу и найти там этот раздел.

Не во всех формулах описываются все учавствующие переменные ((
Так же есть путаница с обозначениями, сперва иксом обозначается расстояние от левой опы до приложенной силы Q, а двумя абзацами ниже иск это уже функция, потом выводятся формули и поехала путаница.

Как-то так получилось, что при решении различных математических задач используется переменная х. Почему? Х его знает. Определение реакций опор при переменной точке приложения силы (сосредоточенной нагрузки) и определение значения момента в некоторой переменной точке относительно одной из опор — это две разные задачи. Более того, в каждой из задач определяется переменная относительно оси х.
Если Вас это запутывает и Вы не можете разобраться в столь элементарных вещах, то ничего поделать не могу. Жалуйтесь в общество защиты прав математиков. А еще я бы на Вашем месте подал жалобу на учебники по строительной механике и сопромату, а то действительно, что это такое? Мало что ли букв и иероглифов в алфавитах?
И еще у меня к Вам встречный вопрос: Вы когда в третьем классе задачки на сложение-вычитание яблок решали, наличие х в десяти задачах на странице Вас тоже путало или как-то справлялись?

Я конечно понимаю, что это не труд какой-то оплачиваемый, но тем не менее. Если идёт формула, то под ней должно быть описание всех её переменых, у Вас же нужно это выискивыть сверху из контекста. А кое где и вообще нет и в контексте упоминания. Я отнюдь не жалуюсь. Я говорю о недостатках работы (за которую уже кстати Вас благодарил). Что касается переменных икс как функции и потом введении ещё одной переменной икс как отрезка, без указаний всех переменный под выводимой формулой вводит путаницу дело тут не в устоявшихся обозначениях, а в целесообразности ведения такого изложения материала.
Кстати вас арказм не уместен, потому как вы излагаете всё на одной странице и без указания всех переменных непонятно, что вы вообще имеете в виду. К примеру в программировании всегда указываются все перменные. Кстати если Вы делаете это всё для народа, то Вам не мешало бы узнать про то какой вклад в математику внёс Кисилёв как педагог, а не как математик, может тогда Вы поймёте о чём я говорю.

Мне кажется, Вы все-таки не совсем правильно понимаете смысл данной статьи и не берете в расчет основную массу читателей. Главная цель была — максимально простыми средствами донести до людей, не всегда имеющих соответствующее высшее образование, основные понятия, используемые в теории сопротивления материалов и строительной механике и зачем все это вообще нужно. Понятное дело, приходилось чем-то жертвовать. Но.
Правильных учебников, где все разложено по полочкам, главам, разделам и томам и описано по всем правилам, хватает и без моих статей. А вот людей, способных сходу разобраться в этих томах, не так уж и много. Во времена моего обучения две трети студентов не понимали смысла сопромата даже приблизительно, а что говорить о простых людях, занимающихся ремонтом или строительством и задумавших рассчитать перемычку или балку? А ведь мой сайт предназначен в первую очередь для таких людей. Я считаю, что наглядность и простота, намного важнее, чем буквальное соблюдение протокола.
Я думал о том, чтобы разбить эту статью на отдельные главы, но при этом необратимо теряется общий смысл, а значит и понимание, зачем это нужно.
Пример с программированием считаю некорректным, по той простой причине, что программы пишутся для компьютеров, а компьютеры по умолчанию тупые. А вот люди — другое дело. Когда жена или подруга говорит Вам: «Хлеб закончился», то Вы без дополнительных уточнений, определений и команд отправитесь в магазин, в котором обычно покупаете хлеб, купите там именно такой хлеб, который обычно покупаете, и именно столько, сколько обычно покупаете. При этом всю необходимую информацию для совершения данного действия Вы по умолчанию извлекаете из контекста предыдущего общения с женой или подругой, имеющихся привычек и других на первый взгляд малозначимых факторов. И при этом заметьте, Вы даже не получаете прямого указания купить хлеб. В этом и есть разница между человеком и компьютером.
Но в главном могу с Вами согласиться, статья не совершенна, как впрочем и все остальное в окружающем нас мире. А на иронию не обижайтесь, в этом мире слишком много серьезности, хочется иногда ее разбавить.

Добрый день!
Ниже формулы 1.2 приводится формула реакции опор для равномерной нагрузки по всей длине балки А=В=ql/2. Мне кажется, что должно быть А=В=q/2, или я чего-то не понимаю?

В тексте статьи все правильно, ведь равномерно распределенная нагрузка означает, какая нагрузка приложена на участке длины балки, и измеряется распределеннная нагрузкка в кг/м. Чтобы определить реакцию опроры, мы сначала находим, чему будет равна суммарная нагрузка, т.е. по всей длине балки.

Извините, все равно не понял :-), буду читать и думать дальше. Просто из формулы вытекает, что чем больше длина балки l (при неизменной нагрузке Q), тем больше реакция опор А и В. Или q и Q — не одно и тоже?

Q — это сосредоточенная нагрузка, какая бы длина балки ни была, значение реакций опор будет постоянным при постоянном значении Q. q — это нагрузка, распределенная по некоторой длине, и потому, чем больше длина балки, тем больше значение реакций опор, при постоянном значении q. Пример сосредоточенной нагрузки — человек, стоящий на мосту, пример распределенной нагрузки — собственный вес конструкций моста.

Вот оно! Теперь понятно. В тексте нет указания, что q — это распределенная нагрузка, просто появляется переменная «ку маленькая», это ввело в заблуждение 🙂

Разница между сосредоточенной и распределенной нагрузкой описывается в вводной статье, ссылка на которую в самом начале статьи, рекомендую ознакомиться.

Не понятно, зачем рассказывать азы сопромата тем, кто строит или проектирует. Если они в вузе не поняли сопромат у грамотных педагогов, то их и близко нельзя допускать до проектирования, а популярные статьи только еще больше их запутают, так как часто содержат грубые ошибки.
Каждый должен быть профессионалом в своей области.
Кстати, изгибающие моменты в приведенных выше простых балках должны иметь положительный знак. Отрицательный знак, проставленный на эпюрах, противоречит всем общепринятым нормам.

1. Далеко не все, кто строит, учились в ВУЗах. И почему-то такие люди, занимающиеся ремонтом в своем доме, за подбор сечения перемычки над дверным проемом в перегородке не хотят платить профессионалам. Почему? спросите у них.
2. Опечаток хватает и в бумажных изданиях учебников, но путают людей не опечатки, а слишком абстрагированное изложение материала. В данном тексте тоже, возможно, есть опечатки, но в отличие от бумажных источников они будут исправлены сразу после того, как будут обнаружены. А вот насчет грубых ошибок, вынужден вас огорчить, здесь их нет.
3. Если вы считаете, что эпюры моментов, построенные снизу оси должны иметь только положительный знак, то мне вас жаль. Во-первых, эпюра моментов достаточно условна и она лишь показывает изменение значения момента в поперечных сечениях изгибаемого элемента. При этом изгибающий момент вызывает в поперечном сечении как сжимающие так и растягивающие напряжения. Раньше было принято строить эпюру сверху оси, в таких случаях положительный знак эпюры был логичным. Затем для наглядности эпюру моментов стали строить так, как показано на рисунках, однако положительный знак эпюр сохранился по старой памяти. Но в принципе, как я уже сказал это не имеет принципиального значения для определения момента сопротивления. В статье по этому поводу сказано: «В данном случае значение момента считается отрицательным, если изгибающий момент пытается вращать балку по часовой стрелке относительно рассматриваемой точки сечения. В некоторых источниках считается наоборот, но это не более чем вопрос удобства». Впрочем объяснять это инженеру нет необходимости, лично я много раз сталкивался с различными вариантами отображения эпюр и никогда проблем это не вызывало. Но по всей видимости статью вы не читали, а ваши высказывания подтверждают, что даже основ сопромата вы не знаете, пытаясь подменить знание некими общепринятыми нормами, да еще и «всеми».

Уважаемый доктор Лом!
Вы невнимательно прочитали мое сообщение. Я говорил об ошибках в знаке изгибающих моментов «в приведенных выше примерах», а не вообще – для этого достаточно открыть любой учебник по сопротивлению материалов, технической или прикладной механике, для вузов или техникумов, для строителей или машиностроителей, написанный полвека назад, 20 лет назад или 5 лет. Во всех без исключения книгах правило знаков для изгибающих моментов в балках при прямом изгибе одно и то же. Это я и имел в виду, говоря об общепринятых нормах. А с какой стороны балки откладывать ординаты – это уже другой вопрос. Поясню свою мысль.
Знак на эпюрах ставят для того, чтобы определить направление внутреннего усилия. Но при этом необходимо договориться, какой знак – какому направлению соответствует. Эта договоренность и является так называемым правилом знаков.
Берем несколько книг, рекомендуемых в качестве основной учебной литературы.
1) Александров А.В. Сопротивление материалов, 2008, с. 34 – учебник для студентов строительных специальностей: «изгибающий момент считать положительным, если он изгибает элемент балки выпуклостью вниз, вызывая растяжение нижних волокон.». В приведенных примерах (во втором параграфе), очевидно, растягиваются нижние волокна, так почему знак на эпюре отрицательный? Или утверждение А. Александрова является чем-то особенным? Ничего подобного. Смотрим дальше.
2) Потапов В.Д. и др. Строительная механика. Статика упругих систем, 2007, с. 27 – вузовский учебник для строителей: «момент считается положительным, если он вызывает растяжение нижних волокон балки».
3) А.В. Дарков, Н.Н. Шапошников. Строительная механика, 1986, с. 27 – широко известный учебник также для строителей: «при положительном изгибающем моменте верхние волокна балки испытывают сжатие (укорочение), а нижние – растяжение (удлинение);». Как видим, правило то же самое. Может быть у машиностроителей все совсем по другому? Опять же нет.
4) Г.М. Ицкович. Сопротивление материалов, 1986, с. 162 – учебник для учащихся машиностроительных техникумов: «Внешняя сила (момент), изгибающая эту часть (отсеченную часть балки) выпуклостью вниз, т.е. таким образом, что сжатые волокна находятся сверху, дает положительный изгибающий момент».
Список можно продолжить, но зачем? Любой студент, сдавший сопромат хотя бы на 4, это знает.
Вопрос, с какой стороны стержня откладывать ординаты эпюры изгибающих моментов, – это уже другое соглашение, которое может полностью заменить выше приведенное правило знаков. Поэтому при построении эпюр М в рамах знак на эпюрах не ставят, так как локальная система координат связана со стержнем, и меняет свою ориентацию при изменении положения стержня. В балках же все проще: это или горизонтальный или наклоненный под небольшим углом стержень. В балках эти два соглашения дублируют друг друга (но не противоречат при правильном понимании). И вопрос, с какой стороны откладывать ординаты, определялся не «раньше, а потом», как Вы пишите, а сложившимися традициями: строители всегда строили и строят эпюры на растянутых волокнах, а машиностроители – на сжатых (до сих пор!). Я бы мог объяснить, почему, но и так много написал. Если бы на эпюре М в приведенных задачах стоял знак «плюс», или вообще не стояло никакого знака (с указанием, что эпюра построена на растянутых волокнах – для определенности), то дискуссии вообще бы не было. А то, что знак М не влияет на прочность элементов при строительстве садового домика, так об этом никто и не спорит. Хотя и здесь можно выдумать особые ситуации.
Вообще, эта дискуссия не плодотворна в виду тривиальности задачи. Каждый год, когда ко мне приходит новый поток студентов, приходится им объяснять эти простые истины, или подправлять мозги, запутанные, что греха таить, отдельными преподавателями.
Отмечу, что из Вашего сайта я почерпнул и полезную, интересную информацию. Например, графическое сложение линий влияния опорных реакций: интересный прием, который не встречал в учебниках. Доказательство здесь элементарное: если сложить уравнения линий влияния, получим тождественно единицу. Наверное, сайт будет полезен умельцам, затеявшим строительство. Но все же, на мой взгляд, лучше пользоваться литературой, опирающейся на СНИП. Есть популярные издания, содержащие не только формулы сопромата, но и нормы проектирования. Там даны простые методики, содержащие и коэффициенты перегрузки, и сбор нормативных и расчетных нагрузок и др.

отличный сайт, спасибо вам! Будьте добры, подскажите, если у меня точечая нагрузка 500 Н каждые полметра на балке длиной 1.4 м, могу я рассчитывать как равномерно распределеную нагрузку в 1000 Н/м? и чему тогда будет равно q?

Владислав
в такой форме я принимаю вашу критику, но все равно остаюсь при своем мнении. Например, есть очень старый Справочник по технической механике, под редакцией акад. А.Н. Динника, 1949, 734 с. Конечно же данный справочник давно устарел и никто им сейчас не пользуется, тем не менее в этом справочнике эпюры для балок строились на сжатых волокнах, а не так, как принято сейчас, и на эпюрах проставлялись знаки. Именно это я и имел в виду, когда говорил «раньше — потом». Еще через 20-50 лет принятые ныне критерии определения знаков эпюр могут опять поменяться, однако сути это, как вы понимаете, не изменит.
Лично мне кажется, что отрицательный знак для эпюры, расположенной ниже оси, более логичен, чем положительный, так как с начальных классов нас учат, что все, что откладывается вверх по оси ординат — положительно, все что вниз — отрицательно. А ныне принятое обозначение — одно из многочисленных, хотя и не основных препятствий к пониманию предмета. Кроме того, у некоторых материалов расчетное сопротивление растяжению намного меньше расчетного сопротивления сжатию и потому отрицательный знак наглядно показывает опасную область для конструкции из такого материала, впрочем, это мое личное мнение. Но то, что ломать копья по этому вопросу не стоит — согласен.
Согласен я и с тем, что лучше пользоваться проверенными и утвержденными источниками. Более того, именно это я постоянно советую своим читателям в начале большинства статей и добавляю, что статьи предназначены только для ознакомления и ни в коем случае не являются рекомендациями по расчетам. При этом право выбора остается за читателями, взрослые люди должны сами прекрасно понимать, что они читают, и что с этим делать.

Anna
Точечная нагрузка и равномерно распределенная нагрузка — это все-таки разные вещи и окончательные результаты расчетов для точечной нагрузки напрямую зависят от точек приложения сосредоточенной нагрузки.
Судя по вашему описанию на балку действуют только две симметрично расположенные точечные нагрузки. В этом случае намного проще воспользоваться готовыми расчетными схемами (для этого перейдите по ссылке http://doctorlom.com/item173.html), чем переводить сосредоточенную нагрузку в равномерно распределенную.

я знаю как рассчитывать, спасибо, не знаю вот какую схему взять правильней, 2 нагрузки через 0,45-0,5-0,45м или 3 через 0,2-0,5-0,5-0,2м условие сая знаю как рассчитывать, спасибо, не знаю вот какую схему взять правильней, 2 нагрузки через 0,45-0,5-0,45м или 3 через 0,2-0,5-0,5-0,2м условие самые неблагоприятные положения, опора на концах.

Если вы ищете наиболее неблагоприятное положение нагрузок, к тому же их может быть не 2 а 3, то в целях надежности имеет смысл просчитать конструкцию по обоим указанным вами вариантам. Если навскидку, то вариант с 2 нагрузками представляется наиболее неблагоприятным, но как я уже говорил, желательно проверить оба варианта. Если запас прочности важнее точности расчета, то можете принять распределенную нагрузку 1000 кг/м и умножить ее на дополнительный коэффициент 1.4-1.6, учитывающий неравномерность распределения нагрузки.

спасибо большое за подказку, ещё один вопрос: а если указанная мной нагрузка будет приложена не на балку, а на прямоугольную плоскость в 2 ряда, кот. жестко защемлена с одной большей стороны посередине, как тогда будет выглядеть эпюра или как тогда считать?

Ваше описание слишком неопределенно. Я понял так, что вы пытаетесь рассчитать нагрузку на некий листовой материал, уложенный в два слоя. Что означает «жестко защемлена с одной большей стороны посередине» я так и не понял. Возможно вы имеете в виду, что опираться этой листовой материал будет по контуру, но что тогда означает посредине? Не знаю. Если листовой материал будет защемлен на одной из опор на небольшом участке посредине, то такое защемление вообще можно не учитывать и считать балку шарнирной. Если это однопролетная балка (не важно листовой это материал или профиль металлопроката) с жестким защемлением на одной из опор, то ее так и следует рассчитывать (см. статью «Расчетные схемы для статически неопределимых балок») Если это некая плита, опертая по контуру, то принципы расчета такой плиты можно посмотреть в соответствующей статье. Если листовой материал будет укладываться в два слоя и эти слои имеют одинаковую толщину, то расчетную нагрузку можно уменьшить в два раза.
Однако листовой материал помимо всего прочего следует проверить на местное сжатие от сосредоточенной нагрузки.

Огромное Вам спасибо! за все то, что вы делаете по простому разъяснению народу, основ расчета строительных конструкций. Мне это лично очень помогло при расчетах для себя лично, хотя у меня
и законченный строительный техникум и институт, а сейчас я пенсионер и уже давно не открывал учебников и СНиПов но пришлось вот вспомнить что в молодости когда то учил и уж больно заумно в основном там все изложено и получается взрыв мозгов, а тут стало все понятно, потому что заработали старые дрожжи и пошла закваска мозгов бродить в нужном направлении. Спасибо еЩе раз.
и

Какие усилия действуют на шарнирную балку с равнораспределенной нагрузкой?

вернулась я к вам, потому что ответа так и не нашла. Попробую объясниь понятнее. Это типа балкона 140*70 cм. Сторона 140 прикручена к стене 4 болтами посередине в виде квадрата 95*46mm. Само дно балкона состоит из перфорированного по центру(50*120) листа алюминиевого сплава и под низом приварены 3 прямоугольные полые профиля, кот. начинаются от точки крепления со стеной и расхoдятся в разные стороны одна паралельно боковой стороне, т.е. прямо, а две другие разные стороны, в углы противоположно закрепленой стороны По кругу есть бардюр 15 см высотой; на балконе могут находится 2 человека по 80 кг в самых неблагоприятных положениях + равнораспределеная нагрузка в 40 кг. Балки в стену не закреплены, всё держится на болтах. Так вот, как мне расчитать какой взять профиль и толщину листа, чтобы дно не дифoрmировалось? Это ведь нельзя считать балкой, всё ведь происходит в плоскости? или как?

Вы знаете, Anna, ваше описание очень напоминает загадку бравого солдата Швейка, которую он задал медицинской комиссии.
Не смотря на столь казалось бы подробное описание, совершенно непонятна расчетная схема, какую перфорацию имеет лист «алюминиевого сплава», как именно расположены и из какого материала изготовлены «прямоугольные полые профиля» — по контуру или от середины к углам, и что это за бардюр по кругу?. Впрочем, я не буду уподобляться медицинским светилам, входившим в состав комиссии и попробую вам ответить.
1. Лист настила все равно можно считать балкой с расчетной длиной 0.7 м. А если лист будет приварен или просто оперт по контуру, то значение изгибающего момента посредине пролета действительно будет меньше. Статьи, посвященной расчету металлического настила, у меня пока нет, но есть статья «Расчет плиты, опертой по контуру», посвященная расчету железобетонных плит. А так как с точки зрения зрения строительной механики не важно, из какого материала изготавливается рассчитываемый элемент, то вы можете воспользоваться изложенными в этой статье рекомендациями по определению максимального изгибающего момента.
2. Настил все равно будет деформироваться, так как абсолютно жесткие материалы пока еще существуют только в теории, а вот какую величину деформации считать в вашем случае допустимой, — это другой вопрос. Можете воспользоваться стандартным требованием — не более 1/250 длины пролета.

Ужасно расстраивает на самом деле вот эта путаница со знаками) 🙁 Вроде бы все понял, и геомхар, и подбор сечений, и устойчивость стержней. Обожаю сам физику, в частности, механику) Но логика этих знаков. >_ если выпуклостью вниз» это логикой понятно. Но в реальном случае — в одних примерах решения задач «+», в других — «-«. И хоть ты тресни. Причем, более того, в одних и тех же случаях, например, левую реакцию RA балки по-разному, относительно другого конца, определят) Хех) Оно понятно, что разница коснется только знака «выпирающей части» конечной эпюры. Хотя. наверное, поэтому, и расстраиваться на эту тему не обязательно) 🙂 Кстати, это тоже не все, иногда в примерах почему-то выбрасывают указанный момент заделки, в уравнениях РОЗУ, хотя в общем уравнении не выбрасывают) Короче, любил всегда классическую механику за идеальную точность и четкость формулировки) А тут. А это ещё теории упругости не было, не говоря о массивах)

Здравствуйте. Будьте добры Приведите пример (задачу) с размерностью Q q L,M в разделе. Рисунок №1.2. Графическое отображение изменения реакций опор в зависимости от расстояния приложения нагрузки.

Если я правильно понял, то вас интересует определение опорных реакций, поперечных сил и изгибающих моментов с помощью линий влияния. Более подробно эти вопросы рассматриваются в строительной механике, примеры можно посмотреть здесь — «Линии влияния опорных реакций для однопролетных и консольных балок»(http://knigu-besplatno.ru/item25.html) или здесь — «Линии влияния изгибающих моментов и поперечных сил для однопролетных и консольных балок»(http://knigu-besplatno.ru/item28.html).

Здравствуйте! Помогите, пожалуйста. У меня консольная балка, на нее по всей длине действует распределенная нагрузка, на крайнюю точку «снизу вверх» действует сосредоточенная сила. На расстоянии 1м от края балки крутящий момент М. Мне нужно построить эпюры поперечной силы и моментов. Не знаю как определить распределенную нагрузку в точке приложения момента. Или ее не нужно считать в этой точке?

Распределенная нагрузка потому и распределенная, что распределена по всей длине и для некоторой точки можно определить только значение поперечных сил в сечении. Это означает, что на эпюре сил никакого скачка не будет. А вот на эпюре моментов, если момент изгибающий, а не вращающий, скачок будет. Как будут выглядеть эпюры от каждой из указанных вами нагрузок вы можете посмотреть в статье «Расчетные схемы для балок» (ссылка есть в тексте статьи перед п.3)

А как же приложенная к крайней точке балки сила F? Из-за нее не будет скачка на эпюре поперечных сил?

Будет. В крайней точке (точке приложения силы) правильно построенная эпюра поперечных сил изменит свое значение с F на 0. Да это и так должно быть понятно, если вы внимательно прочитали статью.

Спасибо Вам, Доктор Лом. Врубился, как делать, все получилось. У вас очень полезные познавательные статьи! Пишите больше, премного Вам благодарен!

Спасибо Вам за статью. Мои технари не могут справится с простой задачей: есть конструкция на четырех опорах, нагрузка от каждой опоры (подпятник 200*200мм)36 000 кг, шаг опор 6 000*6 000 мм. Какая должна быть распределенная нагрузка по полу, что бы выдержать данную конструкцию? (есть варианты 4 и 8 тонн/м2 — разброс очень большой). Спасибо.

У вас задача обратного порядка, когда уже известны реакции опор, а по ним нужно определить нагрузку и тогда вопрос более правильно сформулировать так:» при какой равномерно распределенной нагрузке на перекрытие опорные реакции будут составлять 36 000 кг при шаге между опорами 6 м по оси х и по оси z?»
Ответ: «4 тонны на м^2»
Решение: сумма опорных реакций 36х4=144 т, площадь перекрытия 6х6=36 м^2, тогда равномерно распределенная нагрузка 144/36 =4 т/м^2. Это следует из уравнения (1.1), настолько простого, понять, как можно его не понять, очень трудно. И это действительно, очень простая задача.

Две (три, десять) одинаковых балок (стопка) свободно сложенные друг на друга (концы не заделаны) выдержат большую нагрузку, чем одна?

Да.
Если не учитывать силу трения, возникающую между соприкасающимися поверхностями балок, то две сложенные друг на друга с одинаковым сечением балки выдержат в 2 раза большую нагрузку, 3 балки — в 3 раза большую нагрузку и так далее. Т.е. с точки зрения строительной механики нет разницы, лежат балки рядом или одна на другой.
Однако такой подход к решению задач является неэффективным, так одна балка высотой, равной высоте двух одинаковых свободно сложенных балок, выдержит нагрузку в 2 раза большую, чем две свободно сложенные балки. А балка высотой, равной высоте 3 одинаковых свободно сложенных балок, выдержит нагрузку в 3 раза большую чем 3 свободно сложенные балки и так далее. Это следует из уравнения момента сопротивления.

Спасибо.
Доказываю это конструкторам на примере десантников и стопки кирпичей, тетрадь/одинокий лист.
Не сдаются бабушки.
Армированный бетон у них подчиняется другим законам, нежели дерево.

В чем-то бабушки правы. Армированный бетон — это анизотропный материал и его действительно нельзя рассматривать как условно изотропную деревянную балку. И хотя для расчетов железобетонных конструкций часто используются специальные формулы, но суть расчета от этого не меняется. Для примера посмотрите статью «Определение момента сопротивления»

Спасибо за материал. Подскажите, пожалуйста, методику расчета одной нагрузки на 4 опоры на одной линии — 1 опора левее точки приложения нагрузки, 3 опоры — правее. Все расстояния и нагрузка известны.

Посмотрите статью «Многопролетные неразрезные балки.»

Всё это очень неплохо и довольно доходчиво. НО . у меня вопрос к линеечкам. А вы не забыли при определении момента сопротивления линейки поделить на 6? Чево-то арифметика не сходится.

А энто в какой же хвормуле не сходится? в 4.6, в 4.7, али в другой какой? Поточнее надобно мыслю выражать.

Я в шоке, -оказывается основательно подзабыл сопромат (иначе «технология материалов» ))), но позже).
Док спасибо за Ваш сайт читаю, вспоминаю, все очень интересно. Нашел случайно, — встала задача оценить что выгодней (по критерию минимальной стоимости материалов [принципиально без учета трудозатрат и расходов на оборудование/инструмент] применить в контрукции колонны из готовых профильных труб (квадрат) по расчету, либо приложить руки и сварить колонны самому(допустим из уголка). Эх тряпки-железки, студенчество, как давно это было. Да, ностальгия, есть немного.

Добрый день.Зашел на сайт в надежде понять все же «физику» перехода распределенной нагрузки в сосредоточеную и распределение нормативной нагрузки на всю плоскость площадки, но смотрю что вы и мой предыдущий вопрос с вашим ответом убрали :(( Мои расчетные металлоконструкции и так отлично работают ( беру сосредоточенную нагрузку и все по ней просчитываю-благо сфера моей деятельности эт о вспомогательные приспособления,а не архитектура,чего и хватает с головой),но все же хотелось бы б понять про распределенную нагрузку в контексте кг/м2 — кг/м . У меня нет возможности сейчас узнать у кого либо по этому вопросу ( сталкиваюсь с такими вопросами редко, а как сталкнусь начинаются рассуждения 🙁 ), нашел ваш сайт — адекватно все изложено, так же я понимаю что знания стоят денег. Скажите как и куда я могу вас «отблагодарить» , всего лишь за ответ по предыдущему моему вопросу про площадку,- для меня это действительно важно. Общение можно перенести в е-mail ную форму — мое мыло «Olegggan@mail.ru». Спасибо

Я оформил нашу переписку в отдельную статью «Определение нагрузки на конструкции», все ответы там.

Спасибо, имея высшее техническое образование было приятно почитать. Небольшое замечание — центр тяжести треугольника находится на пересечении МЕДИАН! (у Вас написано биссектрис).

Все верно, замечание принимается — конечно же медиан.

Потребовалось узнать, во сколько увеличится изгибающий момент, если случайно выбить одну из промежуточных балок. Увидел квадратичную зависимость от расстояния, следовательно в 4 раза. Не пришлось лопатить учебник. Большое спасибо.

Для неразрезных балок со множеством опор, все намного сложнее, так как момент будет не только в пролете но и на промежуточных опорах (смотрите статьи по неразрезным балкам). Но для предварительной оценки несущей способности можно использовать указанную квадратичную зависимость.

Не могу понять. Как правильно рассчитать нагрузку для опалубки. Грунт ползет при копки,нужно выкопать яму под септик Д=4.5м,Ш=1.5м, В=2м. Хочу саму опалубку выполнить так: контур по периметру балка 100х100(верх, низ, середина(1м), далее доска сосна 2-сорт 2х0.15х0.05. делаем короб. Боюсь что не выдержит . т.к по моим расчетам доска выдержит 96 кг/м2. Развертка стен опалубки (4.5х2 +1.5х2)х2 = 24 м2. Обьем вынутого грунта 13500кг. 13500/24=562.5 кг/м2. Прав или нет. И какой выход

То, что стенки котлована осыпаются при такой большой глубине — это естественно и обуславливается свойствами грунта. Ничего страшного в этом нет, в таких грунтах траншеи и котлованы копаются со скосом боковых стенок. При необходимости стенки котлована укрепляются подпорными стенками и при расчете подпорных стенок действительно учитываются свойства грунта. При этом давление от грунта на подпорную стенку не постоянное по высоте, а условно равномерно изменяющееся от нуля вверху до максимального значения внизу, а вот значение этого давления зависит от свойств грунта. Если попробовать объяснить максимально просто, то чем больше угол скоса стенок котлована, то тем больше давление будет на подпорную стенку.
Вы разделили массу всего вынутого грунта на площадь стенок, а это не правильно. Этак получается, что если при той же глубине ширина или длина котлована в два раза больше, то и давление на стенки будет в два раза больше. Для расчетов Вам нужно просто определить объемный вес грунта, как — отдельный вопрос, но в принципе сделать это не сложно.
Формулу для определения давления в зависимости от высоты, объемного веса грунта и угла внутреннего трения здесь не привожу, к тому же вы вроде бы опалубку хотите рассчитать, а не подпорную стенку. В принципе давление на доски опалубки от бетонной смеси определяется по тому же принципу и даже немного проще, так как бетонную смесь можно условно рассматривать как жидкость, оказывающую одинаковое давление на дно и стенки сосуда. А если заливать стенки септика не сразу на всю высоту, а в два захода, то соответственно и максимальное давление от бетонной смеси будет в 2 раза меньше.
Далее, доска, которую вы хотите использовать для опалубки (2х0.15х0.05), способна выдерживать очень большие нагрузки. Не знаю, как именно вы определяли несущую способность доски. Посмотрите статью «Расчет деревянного перекрытия».

Спасибо доктор.Расчет я сделал не правильно, ошибку я понял. Если считать следующим образом: длина пролета 2м, доска сосна h=5см, b=15см тогда W=b*h2/6=25*15/6 = 375/6 =62.5см3
M=W*R = 62.5*130 = 8125/100 = 81.25 кгм
тогда q = 8M/l*l = 81.25*8/4 = 650/4 = 162кг/м или при шаге 1м 162кг/м2.
Я не строитель, поэтому не совсем понимаю много это или мало для котлована куда мы хотим впихнуть септик из пластика, или наша опалубка треснет и мы не успеем это все сделать. Вот такая задача, если можете что-то еще подсказать — буду вам признателен. Спасибо еще раз.

Ага. Вы все-таки хотите сделать подпорную стенку на время монтажа септика и, судя из вашего описания, собираетесь это сделать после того, как котлован будет выкопан. В этом случае нагрузка на доски будет создаваться осыпавшимся во время монтажа грунтом и потому будет минимальна и никаких особых расчетов не требуется.
Если же вы собираетесь засыпать и утрамбовать грунт обратно до монтажа септика, то расчет действительно нужен. Вот только расчетную схему вы приняли не правильную. В вашем случае доску, крепящуюся к 3 балкам 100х100, следует рассматривать как двухпролетную неразрезную балку, пролеты у такой балки будут около 90 см, а значит и максимальная нагрузка, которую сможет выдержать 1 доска, будет значительно больше, чем определенная вами, хотя при этом следует еще учесть и неравномерность распределения нагрузки от грунта в зависимости от высоты. А заодно и проверить несущую способность балок работающих по длинной стороне 4.5 м.
В принципе на сайте есть расчетные схемы, подходящие для вашего случая, а вот информации по расчету свойств грунта пока нет, впрочем это уже далеко не основы сопромата, да и по моему мнению вам такой точный расчет не нужен. Но в целом ваше стремление к пониманию сути процессов весьма похвально.

Спасибо доктор! Мысль вашу понял, надо будет еще почитать ваш материал. Да септик нужно впихнуть так чтобы не произошло обрушения. Опалубка при этом должна выдержать, т.к. рядом на расстоянии 4м еще и фундамент и можно все это запросто обрушить. Поэтому я так беспокоюсь. Еще раз спасибо, вы меня обнадежили.

Док, в конце статьи, где вы приводите пример определения момента сопротивления, в обоих случаях забыли разделить на 6. Разница все равно получится в 7,5 раз, но цифры будут другие (0,08 и 0,6) а не 0,48 и 3,6

Верно, была такая ошибка, исправил. Спасибо за внимательность.

добрый день. У меня такой вопрос, как можно посчитать нагрузку на балку. если с одной стороны закрепление жесткое с другой нет закрепленя. длина балки 6 метров. Вот надо посчитать какая должна быть балка, лучше монорельса. макс нагрузка на не закрепленной стороне 2 тонны. заранее спасибо.

Посчитайте, как консольную. Больше подробностей в статье «Расчетные схемы для балок».

Если бы я не изучал сопрамат, то я бы, честно говоря ничего не понял. Если вы пишите популярно, то вы и расписывайте популярно. А то у вас вдруг что-то появляется непонятно откуда, что за х? почему х? почему вдруг x/2 и чем он отличается от l/2 и l? Вдруг появилась q. откуда? Может опечатка и нужно было обозначить Q. Неужели нельзя потробно описать. И момент про производные. Вы понимаете, что вы описываете то, что только вы понимаете. И тот кто читает это впервые он этого не поймет. Поэтому стоило либо расписать подробно, либо вообще удалить этот абзац. Я сам со второго раза понял о чем речь.

Тут, к сожалению, ничем помочь не могу. Популярнее сущность неизвестных величин излагается только в начальных классах средней школы, и я полагаю, что хотя бы этот уровень образования читатели имеют.
Внешняя сосредоточенная нагрузка Q так же отличается от равномерно распределенной нагрузки q, как и внутренние усилия Р от внутренних напряжений р. Более того, в данном случае рассматривается внешняя линейная равномерно распределенная нагрузка, а между тем внешняя нагрузка может быть распределенной и по плоскости и по объему, при этом распределение нагрузки далеко не всегда бывает равномерным. Тем не менее любую распределенную нагрузку обозначаемую маленькой литерой, всегда можно привести к равнодействующей силе Q.
Впрочем, изложить все особенности строительной механики и теории сопротивления материалов в одной статье физически невозможно, для этого есть другие статьи. Почитайте, возможно, что-то прояснится.

Доктор! Не могли бы вы сделать пример расчета монолитного железобетонного участка как балку на 2х шарнирных опорах, при отношении сторон участка больше 2х

В разделе «Расчет железобетонных конструкций» всяких примеров хватает. К тому же постичь глубокую суть вашей формулировки вопроса я так и не смог, особенно вот это: «при отношении сторон участка больше 2х»

добрый. я первый раз встретил сапромат на вашем сайте заинтерисовался. пытаюсь разобраться в основах но понять эпюры Q не получается с М все понятно и ясно и их отличие тоже. Для распределенной Q я на веревку положил например танковый трак или каму что удобно. а на сосредоточенную Q я подвесил яблоко все логично. как на пальцах посмотреть эпюруQ. прошу не цетировать пословицу мне она не подходит я уже женат. спасибо

Для начала рекомендую вас почитать статью «Основы сопромата. Основные понятия и определения», без этого может возникнуть недопонимание изложенного ниже. А теперь продолжу.
Эпюра поперечных сил — условное название, более правильно — график, показывающий значения касательных напряжений, возникающих в поперечных сечениях балки. Таким образом по эпюре «Q» можно определить сечения, в которых значения касательных напряжений максимальны (что может понадобиться для дальнейших расчетов конструкции). Строится эпюра «Q» (как впрочем и любая другая эпюра), исходя из условий статического равновесия системы. Т.е. для определения касательных напряжений в некоторой точке часть балки в этой точке отсекается (потому и сечения), а для оставшейся части составляются уравнения равновесия системы.
Теоретически у балки бесконечное множество поперечных сечений и потому составлять уравнения и определять значения касательных напряжений можно также бесконечно. Вот только нет никакой необходимости делать это на участках, где ничего ни добавляется ни убавляется, или изменение можно описать какой-либо математической закономерностью. Таким образом значения напряжений определяются только для нескольких характерных сечений.
И еще эпюра «Q» показывает некоторое общее значение касательных напряжений для поперечных сечений. Для определения касательных напряжений по высоте поперечного сечения строится другая эпюра и вот она уже называется эпюрой касательных напряжений «т». Больше подробностей в статье «Основы сопромата. Определение касательных напряжений».

Если на пальцах, то возьмем к примеру деревянную линейку и положим ее на две книжки, при этом книжки лежат на столе так, чтобы линейка опиралась на книжки краями. Таким образом получаем балку с шарнирными опорами, на которую действует равномерно распределенная нагрузка — собственный вес балки. Если мы распилим линейку пополам (где значение эпюры «Q» равно нулю) и одну из частей уберем (при этом опорная реакция условно останется прежней), то оставшаяся часть повернется относительно шарнирной опоры и местом распила упадет на стол. Чтобы этого не случилось, в месте распила нужно приложить изгибающий момент (значение момента определяется по эпюре «М» и момент посредине — максимальный), тогда линейка останется в прежнем положении. Это означает что в поперечном сечении линейки, расположенном посредине, действуют только нормальные напряжения, а касательные равны нулю. На опорах нормальные напряжения равны нулю, а касательные — максимальны. Во всех остальных сечениях действуют как нормальные так и касательные напряжения.

Добрый день, объясните пожалуйста почему допустимая опорная реакция в балке в 2 раза больше допустимой поперечноя силы Q по эпюре

Ваш вопрос мне не понятен, так как опорная реакция соответствует значению поперечной силы по эпюре Q. А о допустимости речь можно вести только тогда, когда проверяется на прочность существующая конструкция, а на данном этапе, пока параметры балки не известны, любая нагрузка или напряжение будут допустимыми.

Здравствуйте «Чтобы не углубляться в абстракции математики рассмотрим наглядный пример:» а где сам пример?

Следующий ниже расчет балки на шарнирных опорах на действие сосредоточенной нагрузки, приложенной посредине пролета — это и есть пример применения приведенных выше формул.

Доктор Лом.
Хочу поставить мини тельфер на поворотной консоли, саму консоль прикрепить к регулируемой по высоте металлической стойки(используется в строительных лесах). У стойки есть две площадки 140*140 мм. сверху и снизу. Устанавливаю стойку на деревянный пол, креплю снизу и в распор сверху. Креплю все шпилькой на гайки М10-10мм. Сам пролет 2м, шаг 0.6м, лага пола — обрезная доска 3.5см на 200см, пол шпунтованная доска 3.5 см., потолок лага — обрезная доска 3,5см на 150см., потолок шпунтованная доска 3.5 см. Все дерево сосна, 2-ой сорт нормальной влажности. Стойка весит 10кг, тельфер — 8кг. Поворотная консоль 16 кг, стрела поворотной консоли мах 1м, на стреле крепится сам тельфер в край стрелы. Хочу поднимать до 100кг веса на высоту до 2м. При этом груз после подьема будет стрелой поворачиваться в пределах 180град. Пытался выполнить расчет, но мне это оказалось не под силу. Хотя ваши расчеты по деревянным полам вроде понял. Спасибо, Сергей.

Из вашего описания не понятно, что именно вы хотите рассчитать, по контексту можно предположить, что вы хотите проверить прочность деревянного перекрытия (параметры стойки, консоли и пр. вы определять не собираетесь).
1. Выбор расчетной схемы.
В этом случае ваш подъемный механизм следует рассматривать как сосредоточенную нагрузку, прикладываемую в месте крепления стойки. Будет ли эта нагрузка действовать на одну лагу или на две, будет зависеть от места крепления стойки. Больше подробностей смотрите в статье «Расчет пола в бильярдной комнате». Кроме того, на лаги обеих перекрытий и на доски будут действовать продольные силы и чем дальше груз будет от стойки, тем большее значение будут иметь эти силы. Как и почему объяснять долго, посмотрите статью «Определение вырывающего усилия (почему дюбель не держится в стене)».
2. Сбор нагрузок
Так как вы собираетесь поднимать грузы, то нагрузка будет не статическая, а как минимум динамическая, т.е. значение статической нагрузки от подъемного механизма следует умножить на соответствующий коэффициент (см. статью «Расчет на ударные нагрузки»). Ну при этом не стоит забывать и об остальной нагрузке (мебель, люди и др.).
Так как вы собираетесь кроме шпилек использовать распор, то определить нагрузку от распора — самое трудоемкое занятие, т.к. сначала надо будет определить прогиб конструкций, а уже из значения прогиба определять действующую нагрузку.
Примерно так.

Работаю инженером развертки сетей ИТ(не по профессии). Одна из причин моего ухода с проектирования были расчеты по формулам из области сопромата и термеха(приходилось искать подходящее по рук-вам Мельникова, Муханова итд.. :)) В институте, к лекциям по относился несерьезно. В результате получил пробелы. К моим пробелам в расчетах Гл. спецы относились безразлично, так как сильным всегда удобно когда выполняют их указания. В результате, моя мечта быть профессионалом в области проектирования не сбылась. Всегда беспокоила неуверенность в расчетах(хотя интерес был всегда), соответственно платили копейки.
Спустя годы, мне уже 30, но в душе остается осадок. Лет 5 назад, такого открытого ресурса в интернете не существовало. Когда я вижу что все понятно изложено, хочется вернуться и учиться заново!)) Сам материал просто бесценный вклад в развитие таких как я))), а их возможно и тысячи. Думаю что они как и я будут Вам сильно признательно. СПАСИБО за проделанную работу!

Не отчаивайтесь, учиться никогда не поздно. Часто в 30 лет жизнь только начинается. Рад, что смог помочь.

» М = А • х — Q (x — a) + В(х — l) (1.5)
Например, на опорах никакого изгибающего момента нет и действительно, решение уравнения (1.3) при х=0 дает нам 0 и решение уравнения (1.5) при х=l дает нам тоже 0.»

Не очень понял как решение уравнения 1.5 дает нам ноль. Если подставить l=x, то нулю равно только третье слагаемое В(x-l), а два других нет. Как же тогда М равно 0?

А вы просто подставьте имеющиеся значения в формулу. Дело в том, что момент от опорной реакции А в конце пролета, равен моменту от приложенной нагрузки Q, вот только эти члены в уравнении имеют разные знаки, поэтому и получается ноль.
Например при сосредоточенной нагрузке Q, приложенной посредине пролета опорная реакция А = В = Q/2, тогда уравнение моментов в конце пролета будет иметь следующий вид
М = lxQ/2 — Qxl/2 + 0xQ/2 = Ql/2 — Ql/2 = 0.

Если x расстояние приложения Q то, что такое а, от начала до . Н.: l=25см x=5см в цифрах на примере что будет а

х — это расстояние от начала балки до рассматриваемого поперечного сечения балки. х может изменяться от 0 до l (эль, не единица), так как мы можем рассматривать любое поперечное сечение имеющейся балки. а — это расстояние от начала балки до точки приложения сосредоточенной силы Q. Т.е. при l = 25см, а = 5см х может иметь любое значение, в том числе и 5 см.

Понял. Я почему-то рассматриваю сечение именно в точке приложения силы. Невижу необходимости рассматривать сечение между точками нагрузок так как оно испытывает меньшее воздействие чем последующая точка сосредоточенной нагрузки. Я неспорю просто мне нужно пересмотреть тему занова

Иногда есть необходимость определить значение момента, поперечной силы других параметров не только в точке приложения сосредоточенной силы, но и для других поперечных сечений. Например при расчете балок переменного сечения.

Если приложить сосредоточенную нагрузку на некотором расстоянии от левой опоры — х. Q=1 l=25 x=5, то Rлев=А=1*(25-5)/25=0,8
значение момента в любой точке нашей балки можно описать уравнением М = Р • x. Отсюда M=A*x когда x несовподает с точкой приложения силы, пусть будет рассматриваемое сечение равно x=6, то получаем
M=A*x=(1*(25-5)/25)*6=4,8. Когда я беру ручку и последовательно подставляют свои значения в формулы, то получаю путаницу. Мне надо различить иксы и одному из них присвоить другую букву. Пока я печатал разобрался основательно. Можете не публиковать, но может кому-то это понадобится.

Я уже объяснял, что это два разных икса по той причине, что для обозначения неизвестных переменных обычно используется литера «х». И используются эти иксы для решения разных задач. В первом случае — для определения значений опорной реакции, а во втором — для определения изгибающего момента. Тем не менее, я внес изменения в текст статьи, чтобы подобных вопросов больше не возникало.

Отличная статья. В памяти все восстановилось. Сегодня она была очень кстати!

Здравствуйте доктор. Скажите пожалуйста, каким образом в графическом методе определения реакций, мы определяем значение, т.е. длину прилежащего катета, т.е. длину линии обозначающую реакцию опоры?

Мы пользуемся принципом подобия прямоугольных треугольников. Т.е. треугольник, у которого один катет равен Q, а второй катет равен l, подобен треугольнику с катетами х — значение опорной реакции R и l — a (или а, в зависимости от того, какую именно опорную реакцию мы определяем), из чего следуют следующие уравнения (согласно рисунку 5.3)
Rлев = Q(l — a)/l
Rпр = Qa/l
Не знаю, понятно ли объяснил, но подробнее вроде уже некуда.

Огромное Вам спасибо за работу. Вы очень сильно помогаете многим, в том числе и мне, людям.Всё изложено просто и доходчиво

Здравствуйте. Если Вам не сложно, объясните каким образом вы получили ( вывели) данное уравнение моментов):
МB = Аl — Q(l — a) + В(l — l) (x = l) По полочкам, как говорится. Не сочтите за наглость, просто реально не понял.

Вроде итак в статье все достаточно подробно объяснено, но попробую. Нас интересует значение момента в точке В — МВ. На балку в данном случае действуют 3 сосредоточенные силы — опорные реакции А и В и сила Q. Опорная реакция А приложена в точке А на расстоянии l от опоры В, соответственно она будет создавать момент равный Аl. Сила Q приложена на расстоянии (l — a) от опоры В, соответственно она будет создавать момент — Q(l — a). Минус потому, что Q направлена в сторону, противоположную опорным реакциям. Опорная реакция В приложена в точке В и никакого момента она не создает, точнее момент от этой опорной реакции в точке В будет равен нулю из-за нулевого плеча (l — l). Складываем эти значения и получаем уравнение (6.3).
И да, l — это длина пролета, а не единица.

Здравствуйте! Спасибо за статью, всё намного понятнее и интереснее, чем в учебнике, я остановился на построении эпюры «Q» отображения изменения сил, ни как не могу понять почему эпюра слева устремляется к верху, а с права к низу, как я понял силы что на левой и на правой опоре действую зеркально, то есть сила балки (синяя) и реакции опоры (красная) должны отображаться с обеих сторон, можете объяснить?

Более подробно этот вопрос рассматривается в статье «Построение эпюр для балки», здесь же скажу, что ничего удивительно в этом нет — в месте приложения сосредоточенной силы на эпюре поперечных сил всегда есть скачок, равный значению этой силы.

День добрый! Проконсультируйте см картинка https://yadi.sk/i/CCBLk3Nl3TCAP2. Железобетонная монолитная опора с консолями. Если я консоль делаю не обрезанную, а прямоугольную то по калькулятору сосредоточенная нагрузка на краю консоли 4т при прогибе 4мм, а какая нагрузка будет на эту обрезанную консоль на картинке. Как в таком случае рассчитывается сосредоточенная и распределенная нагрузка при моем варианте. С Уважением.

Сергей, посмотрите статью «Расчет балок равного сопротивления изгибающему моменту», это конечно не ваш случай, но общие принципы расчета балок переменного сечения там изложены достаточно наглядно.

Помогите рассчитать предельную длину консольной балки до достижения жёсткой заделки напряжений равной пределу текучести материала

Добрый день. Строим качель. Хотелось бы узнать какую надо балку для качели при нагрузке в 250кг. Сечение балки у нас 85 мм? Спасибо за помощь.

Для того, чтобы ответить на ваш вопрос, нужно знать расстояние между опорами и что имеется в виду под сечением балки 85 мм. Это диаметр трубы или площадь сечения трубы или еще что-то?

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

💡 Видео