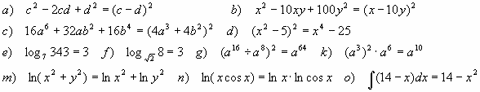Ошибки при решении задач с помощью уравнений (8 видео)

math4school.ru

Содержание

Ошибки в уравнениях
Потеря корней
Посторонние корни
Ошибки, связанные с заменой переменной
Ошибки, связанные с использованием модуля
Подбор корней без обоснования
Ошибки в логарифмических и показательных уравнениях
Ошибки в тригонометрических уравнениях
Диагностика типичных ошибок при решении задач на уроках математики.
Просмотр содержимого документа «Диагностика типичных ошибок при решении задач на уроках математики. »
Трудности при изучении темы « Квадратные уравнения» в 8 классе.
📹 Видео

Видео:Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Ошибки в уравнениях

При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.

Потеря корней

При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней , либо появление посторонних корней .

При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного , а значит, корни могут оказаться потерянными.

K Упражнение. Решить уравнение lg (x – 10) 2 + lg x 2 = 2lg 24 .

L Неправильное решение.

2lg (x – 10) + 2lg x = 2lg 24,

Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.

Комментарий . Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.

J Правильное решение.

Ответ: –2; 4; 6 и 12.

При делении обеих частей уравнения на выражение, содержащее неизвестное , могут быть потеряны корни, которые обращают эти выражения в ноль.

K Упражнение 1. Решить уравнение 3 х ( х 2 – 2 х – 3) = 9 ( х 2 – 2 х – 3) .

L Неправильное решение.

Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:

J Правильное решение.

Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:

K Упражнение 2. Решить уравнение lg 2 x – lg x = 0 .

L Неправильное решение.

Разделим обе части уравнения на lg x и получим:

J Правильное решение.

Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.

Посторонние корни

При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.

Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.

Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину .

K Упражнение. Решить уравнение

5 – x	–	5 + 3х	= 0 .
x – 1		x 2 – 1

L Неправильное решение.

Умножим все члены уравнения на х 2 – 1 и получим:

Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .

J Правильный ответ: х = 0.

Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .

K Упражнение. Решить уравнение

L Неправильное решение.

Заметим, что х 2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9 . Имеем:

Комментарий . Был приобретен посторонний корень х = 9 .

J Правильный ответ: решений нет.

Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.

K Упражнение. Решить уравнение

х 2 – 81

2	+ х 2 –	2	– 4х = 0 .
3х 2		3х 2

L Неправильное решение.

После приведения подобных слагаемых получим:

Комментарий . Был приобретен посторонний корень х = 0 .

J Правильный ответ: 4 .

Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.

Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.

K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .

L Неправильное решение.

И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.

Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения

Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.

Шестерка выходит на арену при переходе от уравнения

которое уже имеет один корень –2 , к уравнению

Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение

для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.

J Правильный ответ: решений нет.

Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.

Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.

K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .

L Неправильное решение.

Перейдем от данного уравнения у совокупности уравнений:

Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.

J Правильный ответ: 5 и 3 .

Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:

x =	x · y
	y

tg ( x + y ) =	tg x + tg y
	1 – tg x · tg y

sin 2 x =	2 tg x
	1 + tg 2 x

В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .

L Неправильное решение.

так как х ≥ 3 , то |х – 1| = х – 1 и

Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений ∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .

Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.

J Правильное решение.

(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)

(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)

(left(x-1 right)^2cdot left(x-4 right)=0;)

Проверкой убеждаемся, что оба корня действительные.

Ошибки, связанные с заменой переменной

При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.

Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .

K Упражнение. Решить уравнение (5 left(x-3 right)^-6=left(x-3 right)^.)

L Неправильное решение.

Сделав замену ( left(x-3 right)^=t), считают, что ( left(x-3 right)^=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.

J Правильное решение.

Верный результат можно получить, сделав замену ( left(x-3 right)^=t), тогда ( left(x-3 right)^=t^2) с продолжением:

Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .

K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .

L Неправильное решение.

Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .

J Правильное решение.

При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .

K Упражнение. Решить уравнение (x^2-4x-sqrt=6.)

L Неправильное (нерациональное) решение.

Чаще всего данное уравнение начинают решать так:

Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.

Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.

J Правильное решение.

и исходное уравнение принимает вид:

А дальше все просто:

Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.

Ошибки, связанные с использованием модуля

При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.

K Упражнение 1. Решить уравнение (sqrt=9.)

L Неправильное решение.

J Правильное решение.

K Упражнение 2. Решить уравнение (sqrt=x+3.)

L Неправильное решение.

Ответ: корнем данного уравнения является любое действительное число.

J Правильное решение.

Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.

K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .

J Правильное решение.

Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:

На каждом из этих промежутков исходное уравнение принимает свой вид.

1) при х ∈ (–∞; 3) исходное уравнение принимает вид:

так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;

2) при х ∈ [3; 4) исходное уравнение принимает вид:

что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;

3) при х ∈ [4; +∞) исходное уравнение принимает вид:

так как 4 ∈ [4; +∞) , то 4 – корень уравнения.

Так как [3; 4)∪ = [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .

Подбор корней без обоснования

К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .

K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .

L Неправильное решение.

Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.

Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.

J Правильное решение.

введем новую переменную x 2 + 3х + 1 = t , тогда

1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;

Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.

K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .

L Неправильное решение.

Методом подбора находим корень уравнения х = 1 .

Комментарий . Не приведено обоснование единственности подобранного корня уравнения.

J Правильное решение.

Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.

Ошибки в логарифмических и показательных уравнениях

Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.

При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.

K Упражнение 1. Решить уравнение (log₇ x) 1 /₃ = 1 .

L Неправильное решение.

Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.

Ответ: корней нет.

J Правильное решение.

Возведем в куб обе части уравнения, тогда

K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .

L Неправильное решение.

Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:

J Правильное решение.

Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда

Необходимо помнить, что:

из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;

степенно–показательное уравнение предпочтительно решать путем логарифмирования.

При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.

L Неправильное решение.

Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).

J Правильное решение.

K Упражнение 2. Решить уравнение lg x 2 = 4 .

L Неправильное решение.

J Правильное решение 1.

2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.

J Правильное решение 2.

lg x 2 = lg 10000; x 2 = 10000; x = ±100.

Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.

Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .

K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _>^2 ;x=0.)

L Неправильное решение.

(left(1 +2 log _xright)log _x=0;)

Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.

J Правильное решение.

Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.

K Упражнение 2. Решить уравнение (20log_sqrt+ 7log_x^3-3log _x^2=0.)

L Неправильное решение.

Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.

J Правильное решение.

Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.

Ошибки в тригонометрических уравнениях

Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.

Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .

Видео:АЛГЕБРА 7 класс : Решение задач с помощью уравнений | ВидеоурокСкачать

Диагностика типичных ошибок при решении задач на уроках математики.

Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.

Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.

Просмотр содержимого документа
«Диагностика типичных ошибок при решении задач на уроках математики. »

на РМО математиков

«Диагностика типичных ошибок

при решении задач»

МБОУ «Ливенская СОШ №1»

Чебакова Галина Владимировна

«На ошибках учатся», — гласит народная мудрость. Но для того, чтобы извлечь урок из негативного опыта, в первую очередь, необходимо увидеть ошибку. К сожалению, школьник зачастую не способен ее обнаружить при решении той или иной задачи.

Целенаправленная работа над ошибками требует их систематизации. При этом главную роль должны сыграть группы ошибок, которые объединены общими причинами их появления, общей методикой работы над ними. Такая систематизация ошибок позволяет наметить пути их исправления и предупреждения этих ошибок в дальнейшем.

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

1. Ошибки и недочёты, которые обусловлены невниманием к формированию теоретико-множественных представлений учащихся:

ошибки, связанные с недостаточно чётким владением понятиями множества, элемента множества, отношения принадлежности, равенства множеств;

ошибки, которые возникают в результате недостаточно чёткого владения операциями пересечения и объединения множеств.

2. Ошибки, которые связаны с недостаточной логической подготовкой учащихся:

ошибки, связанные с непониманием структуры теоремы;

ошибки, которые обусловлены непониманием зависимости между прямой и обратной теоремами;

ошибки, связанные с непониманием метода доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за отсутствия и неустойчивости самоконтроля.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.

Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.

Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.

Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Проанализируем некоторые типичные ошибки учащихся, допускаемых при решении тренировочных заданий для подготовки к ГИА

Зачастую при решении задач на движение учащиеся не обращают внимание на то, что скорость дана в одних единицах измерения, а время или расстояние в других, поэтому логически рассуждение строится верно, но в результате задача не решена. Что очень важно при ГИА, ЕГЭ – 1 части.

При сопоставлении текста задачи и уравнения для её решения уч-ся обозначают за х не ту величину, которая предложена им в задании.

(Скорость первого велосипедиста на 3 км/ч больше скорости второго, поэтому на путь длинной 20 км ему потребовалось на 20 мин. Меньше, чем второму. Чему равны скорости велосипедистов? Пусть х км/ч скорость первого велосипедиста.)

При решении задач на проценты ( подорожание , скидки) учащиеся повторное изменение величины находят, не применяя правила нахождения части от предыдущей цены, путём сложения и вычитания процентов.

(Магазин закупил на складе футболки и стал продавать их по цене, приносящей доход в 40 % . В конце года цена была снижена на 50 %. Какая цена меньше: та, по которой магазин закупил футболки, или цена в конце года – и на сколько процентов .

Типичные ошибки: 100+40-50=90% Разница на 10 %.))

Рассмотренные ошибки и недочёты типичны на всех ступенях обучения.

Рассмотренные ошибки свидетельствуют о том, что ученики, не справившиеся с решением задач, не смогли представить себе жизненной ситуации, отраженной в задаче, не уяснили отношений между величинами в ней, зависимости между данными и искомым, а поэтому просто механически манипулировали числами.

Почему учащиеся допустили много ошибок при повторном решении знакомых задач? Анализ результатов позволяет сделать вывод о том, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного или графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учитель нередко ограничивается правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания, т.е. не проводятся все этапы работы над задачей.

Для устранения этих недостатков необходимо прежде всего улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.

Типичные методические ошибки учителя при работе с текстовыми задачами

Ошибка 1. Пропуск этапа анализа условия задачи.

«Прочитайте условие задачи. Кто пойдет к доске?» – такое часто можно видеть на уроке. И сразу начинается оформление решения. Этап анализа отсутствует и в некоторых учебниках, и в решебниках. Может быть, проведение этого этапа обязательно не для всех учащихся. В классе найдутся такие ученики, у которых этап анализа свернут. Они его проходят очень быстро, поэтому сразу видят решение и переходят к его оформлению. Задача педагога – помогать тем, у которых не получается. Решение задачи основывается на тех связях, которые существуют между данными и искомыми величинами. На выделение этих связей и направлен анализ условия задачи. Чтобы помочь учащимся самостоятельно осуществлять анализ условия, преподаватель может предложить им специальные памятки.

Ошибка 2. Пропуск этапа поиска решения.

Пропуск этого этапа ведет к недопониманию учащимися сущности эвристической деятельности, и как результат, к возникновению трудностей при самостоятельном решении задач. В практике обучения традиционной является ситуация, когда учитель вызывает к доске учащегося, который знает, как решить задачу. Однако при личностно ориентированном обучении основная забота учителя должна быть связана с теми, кто испытывает затруднения при самостоятельном решении задач.

Тем же учащимся, которые без учителя могут решать задачи, необходимо подбирать задания, усиливающие их умения и способствующие их развитию (составить задачи на основе справочных данных; рассмотреть другие способы решения предложенной задачи; составить граф-схемы других уравнений по задаче и др.)

Ошибка 3. Пропуск этапа исследования решения.

Зачем нужен этот этап? На этапе исследования выясняем, соответствует ли полученный ответ условию задачи (правдоподобность результата); есть ли другие способы решения; что полезного можно извлечь на будущее из решенной задачи. Последний вопрос позволяет рассматривать каждую задачу как звено в общем умении решать задачи, что ведет к накоплению опыта по решению задач.

Ошибка 4. Смешение этапов анализа и поиска решения.

Чтобы этого избежать, надо точно знать, какую цель мы преследуем на каждом этапе. Цель этапа анализа условия – выявить все имеющиеся связи между данными и искомыми величинами, чему помогает составление таблицы (схемы, рисунка). Цель этапа поиска решения – выбрать метод решения (алгебраический или арифметический) и составить план решения. Цели этапов разные, значит, и смешивать эти этапы никак нельзя.

Если для решения задачи выбран алгебраический метод, то поиск ведем по следующим этапам:

определяем условия, которые могут быть основанием для составления уравнения, и выбираем одно из них;

составляем схему уравнения, соответствующего выбранному условию;

определяем, какие величины можно обозначить за х; выбираем одну из них;

определяем, какие величины нужно выразить через х, и находим условия, которые позволяют это сделать.

Завершается этап поиска составлением плана решения задачи.

Ошибка 5. На этапе анализа условия фиксируются не все связи между величинами.

Надо стараться зафиксировать как можно больше таких связей. Почему это важно? Упустив какую-нибудь связь, мы можем потерять:

условие для составления уравнения;

возможность одну величину выразить через другие;

предусмотреть несколько способов решения.

Ошибка 6. Поиск решения задачи алгебраическим методом начинается с выбора переменной.

Обратим внимание на то, что при перечислении этапов, которые мы проходим при поиске решения задачи алгебраическим методом, сначала был назван выбор условия для составления уравнения, затем составление схемы уравнения, и только тогда мы вводим переменную. На практике мы почти везде видим иное: сначала вводят переменную, затем выражают остальные величины через нее и затем составляют уравнение. Вот этот момент настолько «закостенел» в нашем сознании, что от него отказаться очень трудно.

На самом деле, лучше делать «по-новому». Представьте себя на месте ученика в классе. Рассмотрим ситуацию, когда не были проведены этапы анализа и поиска решения, к доске вызван ученик, который знает, как решить задачу, и он начинает: «За х обозначим…» И что же наш ученик, который затрудняется в самостоятельном решении? Мы из решения сделали тайну непостижимую. «Как он угадал, что обозначить за х?» И когда он будет пробовать дома решать задачу, у него сразу закрадывается сомнение: «А вдруг я не угадаю?»

И насколько спокойнее и увереннее чувствует себя наш ученик, если у него есть карточка по проведению анализа и поиска решения задач; он смог составить по условию задачи таблицу; найти несколько условий для составления уравнений; записать схему уравнения для выбранного условия. Ученик знает, что за х можно обозначить любую из неизвестных величин, и, если не получится уравнение по одной схеме, то можно попробовать составить его по другой схеме.

Ошибка 7. Постановка частных, подсказывающих вопросов учащимся.

Очень много зависит от умения ставить (задавать) вопросы учащимся. Вопросы не должны нести в себе подсказку, а подталкивать учащихся к размышлению. Вместо вопросов: «Во сколько туров проходила олимпиада?», «Как распределились посевные площади?», «Какое время находились туристы в пути?», «Какие машины находятся в автопарке?» лучше задавать общие вопросы: «Что происходит по условию задачи?», «Какие объекты участвуют в задаче?», «Какие части можно выделить в задаче?». Вместо вопроса «Можно ли найти такую-то величину?» лучше задать вопрос: «Что можно найти по данным задачи?», поскольку он может вывести на несколько вариантов решения.

Задавая вопросы, учитель не должен вести учащихся к своему решению; нужно рассмотреть все пути решения, выслушать и обсудить все варианты.

2.Для осуществления целенаправленных мер по исправлению и предупреждению ошибок учителю необходимо систематически изучать ошибки учащихся, выявлять наиболее устойчивые и типичные из них, вести учёт распространённых и индивидуальных ошибок учащихся. Знание учителем типичных ученических ошибок, а также причин их возникновения и проявления даёт ему возможность предвидеть и предупреждать их появление. Достичь этого можно путём подбора таких упражнений, которые препятствуют образованию односторонних ассоциаций и неправильных обобщений.

Ошибки учащихся, которые регистрирует и учитывает учитель, помогают ему установить, что не понимают учащиеся, что ими плохо усвоено; это даёт возможность учителю своевременно ликвидировать пробелы в знаниях учащихся и внести соответствующие коррективы в дальнейшее преподавание с целью предупреждения повторения аналогичных ошибок.

Чтобы определить сущность допускаемых учащимися ошибок, необходимо проследить ход рассуждений, который приводит к такому ошибочному решению, установить этап, на котором зарождаются такие ошибки. Как показывает опыт, часто учащемуся непонятен не весь материал, а лишь какая-то его часть. Выявив, что именно непонятно ученику, можно сосредоточить на этом материале всё внимание, не отвлекаясь на те моменты, которые уже усвоены.

Допускаемые учеником ошибки свидетельствуют не только о недостатках его знаний, но и о потенциальных возможностях. Ошибки служат также показателем проблем, которые могут быть поставлены перед учеником, а иногда они приводят к созданию проблемных ситуаций, которые необходимы в данный момент для развития действий.

Ни в коем случае нельзя снижать оценок ученикам за ошибки в процессе поиска. Очень важно приучить их не бояться допускаемых ошибок. Ошибки, допускаемые учениками, надо исправлять тактично, обоснованно, привлекая к этой работе самих учащихся.

Боязнь допустить ошибку сковывает инициативу ученика. Боясь ошибиться, он не будет сам решать поставленную проблему, а станет ждать помощи от учителя. Он будет решать только лёгкие проблемы. Но без такого самостоятельного решения задач с последовательно нарастающей сложностью не может происходить интеллектуальное развитие. Во многих случаях по этой причине учащиеся проявляют робость и интеллектуальную пассивность, что в дальнейшем приводит к неуспеваемости.

Очень оживлённо воспринимаются учащимися “Задачи на выявление ошибки”. Речь идёт не только о софизмах, но и об ошибках, которые допускают сами школьники. Не нужно специально исправлять каждое ошибочное утверждение школьника. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Если они и не допускают ошибок, то всё же нередко целесообразно проверить, насколько они “устойчивы” против типичных ошибок.

Например: Найти ошибки:

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; в) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;

проверка правильности решения задач путём составления и решения задач, обратных к данной;

оценка результата решения задачи с точки зрения здравого смысла;

проверка аналитического решения графическим .

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Пусть решение ученика выглядит так: 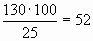. Ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130”. Такая прикидка в уме полезна при решении задач с дробными числами и процентами.

В жизненной практике в чертежах, схемах, расчётах, с которыми ребята будут встречаться, могут быть и ошибки. Если не научить их критически относиться к данным, то могут быть и аварии, и брак, и серьёзные упущения в работе. Чтобы этого избежать, необходимо формировать у учащихся умение анализировать данные, способность обнаруживать встречающиеся ошибки и обосновывать ошибочность положения.

Польский математик Г. Штейнгауз, отмечая большое значение работы над математическими ошибками для активизации мыслительной деятельности учащихся, пишет:

“Если учащегося заверить, что в предложенном ему доказательстве есть ошибка, то можно быть уверенным даже без специальной проверки, что материал будет изучен полностью и очень тщательно”. Поэтому составление списка математических ошибок и использование его в учебных целях является одним из важных факторов повышения эффективности обучения.

Таким образом, важную роль в предупреждении ошибок играет продуманная организация изучения нового материала. Изучение нового материала надо строить так, чтобы ученик был активным участником этого процесса. Не надо бояться, если при первом изложении материала им будут допускаться ошибки, высказываться необоснованные выводы. Важно, чтобы те или иные ошибки в понимании материала исправлялись в зародыше, чтобы ученики воспринимали материал осознанно.

Такому подходу к изучению нового материала способствует создание проблемной ситуации и решение её учащимися под руководством учителя. На таких уроках ученики проходят через следующие стадии: поиск нового, возможное появление ошибок в процессе поиска нового, обоснованное опровержение этих ошибок, снова поиски, в результате которых приходят к правильной догадке, и, наконец, доказательство составленного в поисках предложения. Всё это способствует развитию математического мышления.

Текстовые задача — это способ стимулирования мыслительной активности. Считаю необходимым сформировать такой подход к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения. Необходимо построить процесс обучения математике так, чтобы обеспечить успешное овладение учащимися методами и приемами решения задач и создать условия для формирования у них ряда общенаучных умений — таких, как анализ, синтез, обобщение, сравнение, аналогия.

Необходимо организовать деятельность учащихся на учебном занятии таким образом, чтобы она способствовала формированию исследовательской культуры.

Предлагаю на занятии несколько приемов организации интенсивной мыслительной деятельности, которые используются мною на различных этапах процесса обучения: при актуализации знаний, первичном усвоении материала, его осмыслении, применении и обобщении.

Это можно сделать на следующем содержании материала:

Это задачи, условия которых содержат упоминания, указания, намеки или другие побудители, подталкивающие учащихся к выбору ошибочного пути решения или неверного ответа. Попадая в заранее подготовленную ловушку, ученик испытывает досаду, сожаление оттого, что не придал особого значения тем нюансам условия, из-за которых он угодил в неловкое положение. Простое сообщение о том, что учащиеся, как правило, допускают в заданиях такого-то рода ошибки, несравнимо менее действенно. Ибо оно, несмотря на общность, не является для конкретно взятого ученика личностно значимым, поскольку, во-первых, события, о которых сообщается, происходили когда-то давно, в прошлом, не сейчас, а во-вторых, каждый из учащихся наивно полагает, что в число неудачников сам он не попадает.

Дидактическая ценность этих задач в том, что они служат предупреждением от различного рода ошибок и заблуждений.

Провоцирующие задачи обладают высоким развивающим потенциалом, они способствуют воспитанию одного из важнейших качеств мышления- критичности, приучают к анализу воспринимаемой информации, ее разносторонней оценке, повышают интерес школьников к занятиям математикой.

Я использую такие разновидности провоцирующих задач:

условия, в которых навязывают неверный ответ;

условия, которые подсказывают неверный путь решения;

условия, вводящие в заблуждение из-за неоднозначности трактовки и т.д.

В качестве примера приведу задачи, побуждающие выбор неверного способа решения.

Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?

Или, на уроке в 6 классе по теме «Простые и составные числа» предлагаю задание: «Какие из чисел 205, 206, 207, 208, 209, 210 являются простыми?»

2.Задачи стандартные с нестандартным решением.

Это задачи, при предъявлении которых учащиеся не знают заранее ни способа их решений, ни того, на какой учебный материал опирается решение. Иными словами, учащиеся в ходе решения таких задач должны провести поиск плана решения задачи, установить, какой теоретический материал дает ключ к тому или иному решению. Незначительная обработка условий той или иной задачи из учебника, изменение места и времени ее постановки существенно меняют ее дидактическую значимость, оставляя неизменным практическое содержание.

Проиллюстрирую сказанное примером. Стандартная задача для учащихся 7 класса: «В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Сколько фазанов и кроликов в клетке?». Данную задачу предлагаю решить не алгебраическим способом, приводя к стандартному уравнению, а арифметическим. Таким образом, по существу, данную задачу превращаем в нестандартную для шестиклассников и даже семиклассников.

Задачи такого плана всегда органически связаны с изучаемым материалом. Допуская нестандартное решение, приучаю школьников не довольствоваться шаблоном, а нацеливаю на вдумчивый подход, воспитываю стремление как можно лучше выполнить порученное дело. Они развивают гибкость, рациональность, целенаправленность математического мышления и ценны тем, что дается возможность каждому ученику с любой структурой мышления проявить себя.

Это задачи, алгоритм решения которых неизвестен до начала решения. Главное в том, чтобы открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.

Задачи такого плана решаются исследовательским методом и этим очень интересны для учащихся. Ведь исследование предполагает творчество. Проблемы, которые ставятся перед учащимися, могут иметь разнообразный характер: введение в новую тему, решение задачи новым более эффективным способом, связь известного учебного материала с новым и т.д.

При подборе проблемных задач учитываю знания учащихся и уровень развития их логического мышления, поскольку непосильная задача порождает неуверенность в своих силах и в дальнейшем отвращение от решения любых задач, а излишне простая вводит в заблуждение относительно уровня собственных знаний и умений, не стимулирует поисковую деятельность.

Самое главное- это суметь правильно поставить вопрос, заинтриговать учащихся, создать проблему, а не дать ответ, решив ее. Учащиеся познают понятия, закономерности, теории в ходе поиска, наблюдения, анализа фактов, мыслительной деятельности, результатом чего является знание.

Приведу пример задачи из темы «Смежные углы» (геометрия 7 класс).

Найти два смежных угла, один из которых больше другого на прямой угол.

Возможны различные варианты решения, в частности, алгебраический и геометрический. Здесь проблемный характер проявляется в неявной форме, но ученики понимают непригодность геометрического способа решения.

Другой пример. В 5 классе в ходе изучения темы «Сравнение десятичных дробей» предлагаю вариант решения задания на сравнение дробей 0,31 и 0,6 ученика Петрова. Если целые части дробей равны, сравним дробные части: 316, значит, 0,310,6. Согласны ли вы с таким решением? Начинается обсуждение, поиск, анализ решения.

Логические задачи.(задачи-шутки, таблицы, верные и неверные утверждения, здравый смысл)

Это задачи, ведущие к формированию важнейших характеристик творческих способностей: беглость мысли, гибкость ума, оригинальность, любознательность, умение выдвигать и разрабатывать гипотезы.

Опыт работы показывает, что глубокие, прочные и, главное, осознанные знания могут получить все школьники, если развивать у них не столько память, сколько логическое мышление. Логика учит, как нужно рассуждать, чтобы наше мышление было определенным, связанным, последовательным, доказательным и непротиворечивым. В математике приходится путем рассуждений выводить разнообразные формулы, числовые закономерности, правила, доказывать теоремы.

Основные методы решения логических задач:

метод кругов Эйлера;

Метод рассуждений сопровождаю схемами, чертежами, краткими записями, вырабатывая умения выбирать информацию, пользоваться правилом перебора.

Так, при изучении темы «Степень» в 7 классе, я даю задание: запишите степени x, x 2 , x 3 , x 4 , x 5 , x 6 , x 7 , x 8 , x 9 в пустые клетки квадрата так, чтобы произведение их по любой горизонтали, вертикали и диагонали было равно x в 15 степени. Можно рассказать о магическом квадрате, тогда задача станет еще интереснее для учеников.

Видео:Решение задач с помощью уравнений.Скачать

Трудности при изучении темы « Квадратные уравнения» в 8 классе.

Трудности при изучении темы « Квадратные уравнения» в 8 классе. Традиционные ошибки, допускаемые учащимися при изучении этой темы.

Акулова О.Н., учитель математики высшей категории МАОУ «СОШ №7» г. Гая Оренбургской области

Прежде, чем приступить к изучению данной темы, мы должны знать трудности изучения темы и те традиционные ошибки, которые допускают учащиеся при изучении данной темы.

Во первых, ученики часто применяют нерациональные приемы решения и излишне подробно записывают процесс преобразования данного уравнения к простейшему виду. Выучив формулу решения полного квадратного уравнения, учащиеся, нередко, применяют ее и в случае решения квадратных уравнений с четным коэффициентом при неизвестном в первой степени. Таким образом, большее внимание в процессе обучения следует уделять рациональным способам вычисления корней.

Наиболее часто встречающиеся ошибки в работах учеников 8-го класса при решении квадратных уравнений, относятся к операциям с буквенными коэффициентами. На вопрос, что называется коэффициентом, получаем один ответ: числовой множитель, стоящий перед буквенным выражением. Этот факт подтверждает, что при оперировании с буквами ученики 8-го класса не всегда видят их конкретный смысл. Если бы ученики были приучены контролировать свою работу, они придавали (хотя бы мысленно) численные значения буквам и сами вскрывали свои ошибки. Следовательно, при обучении большее внимание следует обращать на нахождение числовых значений алгебраических выражений и на аналогию в выполнении алгебраических и арифметических действий; тем самым, учащиеся будут привыкать смотреть на буквенное выражение не только как на объект для тождественных преобразований, но и как на функцию входящих в него букв.

Теорема Виета при изучении квадратных урав нений является наиболее сложной темой. Нередко ее смысл учащиеся усваивают формально и не мо гут применить теорему на практике. Для проверки понимания теоремы и знаний по данной теме, ре комендуется предлагать следующие обучающие- воп росы.

Известно, что сумма двух искомых чисел и их произведение — целые числа. Могут ли эти искомые числа быть дробными? Объясните на примерах.

Известно, что сумма и произведение корней квадратного уравнения — целые числа. Могут ли корни этого уравнения быть дробными числами?
Объясните на примерах.

Известно, что сумма корней квадратного урав нения (или сумма двух чисел) — число дробное, а произведение этих чисел — число целое. Могут ли
корни этого уравнения быть целыми числами?

Известно, что сумма корней и их произведе ние — числа дробные. Могут ли корни данного урав нения быть целыми числами. Приведите примеры для различных случаев.

Дано полное квадратное уравнение неприведенного вида, свободный член и коэффициенты которого не имеют общего множителя. Какими числами может выражаться сумма и произведение его корней? Приведите примеры неприведенных полных квадрат ных уравнений для случая:

а)когда и сумма, и произведение их корней выра жаются дробными числами;

б)когда только сумма или только произведение выражается дробным числом.

Могут ли в указанных случаях оба корня быть целыми?

Изучая ошибки по рассматриваемой теме, мы пришли к выводу, что теорему Виета целесообразно изучать индуктивным путем, исходя из рассмотрения приведен ного квадратного уравнения вида x 2 +рх+ q = 0. Затем перейти к рассмотрению этого вопроса для неприве денного квадратного уравнения вида ах 2 + b х + с = 0 и установить соотношение (- b / a )= p и ( c / a )= q

Исследование корней квадратного уравнения по его дискриминанту и коэффициентам, исследование вопроса, будут ли корни данного квадратного уравне ния действительными, различными или равными или среди действительных чисел нет корня данного урав нения, не затрудняет учащихся. Обычно, допускае мая ошибка состоит в том, что за дискриминант при нимают не подкоренное выражение, а квадратный корень из дискриминанта, то есть считают, что D =√( b 2 -4 ac ) или D ₁ =√(( b /2) 2 — q ) при исследовании корней уравнения школьники часто применяют не рациональный прием, который состоит в том, что для ответа на вопросы: будут ли корни данного квадратного уравнения действительными числами, будут ли они различны или равны, учащиеся вычисляют дискриминант, хотя достаточно только установить его
знак. Заметим еще, что не всегда учащиеся умеют самостоятельно указать квадратное уравнение, заве домо имеющее действительные корни без нахождения числовой величины его дискриминанта. Только после приведения нескольких аналогичных примеров квадратных уравнений с отрицательным свободным членом и наводящего вопроса, учащиеся могут сделать вывод, что в этих случаях всегда D > 0 (сказывается недостаточный навык вычитания отрицательного числа). При определении знаков корней квадратного уравнения не всегда можно получить полное, последова тельное, доведенное до логического конца объясне ние процесса исследования без наводящих (и даже подсказывающих) вопросов учителя.

Четкость речи, как известно, связана с осознанно стью соответствующей мысли. Поэтому при объяснении данного вопроса учитель должен дать четкий об разец рассуждений. Прежде всего надо указать, что о знаках корней можно говорить лишь тогда, когда они существуют (во множестве действительных чисел).

Надо убедиться в неотрицательности дискриминанта, причем для этого не следует доводить до конца вычисления, достаточно убедиться, что он не отрица телен (в случае, когда свободный член квадратного уравнения отрицателен, а коэффициент при х 2 поло жителен, не надо вычислять дискриминант — он положителен). Затем рассмотреть на примерах все четыре возможных случая: оба корня уравнения отрицательные, положительные, один из корней отрица тельный, положительный. Выводы следует оформить таблицей.

Вопрос об оперировании с абсолютными величи нами остается слабым местом в знаниях учащихся 8-го класса. Особое внимание надо обратить на тот факт, что сравнение абсолютных величин корней не легко усваивается школьниками. Следует лишний раз подчеркнуть, что, например, число может быть записано в виде | + 6 |; + 6; | — 6 |; 6. Для достижения хо роших результатов можно рекомендовать систему уп ражнений с использованием наглядности.

Расположите в порядке возрастания (убывания) ряд чисел, среди которых имеются положительные, отрицательные числа и нуль. Покажите на числовой прямой числа : — 2,5; 4; — 3; + 2; — 0,1; 1/2; -3/4; — 1/3.

Расположите в порядке возрастания или убы вания абсолютные величины тех же чисел. Сделайте выводы.

Найдите сумму, разность, произведение, част ное абсолютных величин двух чисел, если компонен тами действий служат различные действительные числа в различных комбинациях, не исключая и нуля.

Составление квадратного уравнения по формуле (х — х ₁ )(х — х ₂ )=0 подготавливает учеников к даль нейшему изучению теории алгебраических уравнений. Уже первые примеры на квадратные уравнения- учащиеся решают разложением левой его части на линейные множители, делают необходимые выводы и устанавливают связи между различными вопросами одной и той же темы.

К изучению данного учебного материала учащихся следует готовить, начиная с 5-го класса:

При изучении квадрата числа, натуральной степени учащиеся выполняли такие задания: Найти значение выражения D = b 2 -4 ac , если a =2, b =5, c =4. При изучении десятичных дробей, обыкновенных дробей, отрицательных чисел – a , b , c меняются.

Знание квадратов натуральных чисел от 1 до 20 нужно проверять на протяжении всех лет обучения математики.

К работе по схеме учащиеся готовятся, начиная с устного счета, по цепочке, с указанием порядка действий, с помощью стрелок, по элементарным программам при работе с микрокалькулятором, при прохождении многих тем учащиеся учатся выполнять те, или другие преобразования по алгоритму. У учащихся должны быть отработаны навыки решения линейных уравнений.