- Тема 2: Отбор факторов, включаемых в модель множественной регрессии
- Ошибка спецификации эконометрической модели уравнения регрессии
- Ошибка спецификации
- Смотреть страницы где упоминается термин Ошибка спецификации
- Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
- 🔍 Видео
Видео:Множественная регрессия в ExcelСкачать
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
2. Для регрессионной модели вида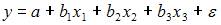 
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.
4. В модели вида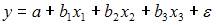 
количество объясняющих переменных равно …
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 
, где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 
– случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
5. При идентификации модели множественной регрессии 
количество оцениваемых параметров равно …
Решение:
При оценке модели множественной регрессии рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии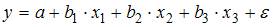 
определитель матрицы парных коэффициентов корреляции между факторами 
, 
и 
близок к единице. Это означает, что факторы , и …
Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы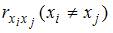 
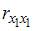
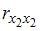
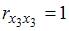
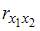
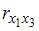
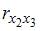
были бы равны нулю.
, поскольку 
= 
= 
и 
= 
= 
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
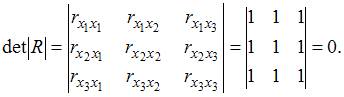
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать
Ошибка спецификации эконометрической модели уравнения регрессии
Видео:Эконометрика. Линейная парная регрессияСкачать
Ошибка спецификации
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения. [c.36]
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис- [c.36]
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. [c.37]
В чем состоят ошибки спецификации модели [c.88]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4. [c.239]
| Рис. 5.4. Ошибка спецификации при выборе уравнения тренда |  |
Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных. [c.338]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных. [c.80]
Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным. [c.15]
Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры. [c.424]
Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]
Как обнаружить ошибку спецификации [c.190]
Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации. [c.192]
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь [c.195]
Как можно обнаружить ошибки спецификации [c.202]
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]
Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]
Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. [c.228]
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции. [c.228]
PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции. [c.228]
Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой. [c.252]
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема. [c.267]
Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации. [c.279]
Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели. [c.181]
Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты). [c.183]
Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться. [c.430]
Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д. [c.423]
Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]
Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4. [c.183]
Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике. [c.477]
В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]
Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика. [c.422]
Смотреть страницы где упоминается термин Ошибка спецификации
Экономико-математический словарь Изд.5 (2003) — [ c.338 ]
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать
Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
| Название | Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие |
| Дата | 02.02.2019 |
| Размер | 1.2 Mb. |
| Формат файла |  |
| Имя файла | Baza_po_ekonometrike.doc |
| Тип | Документы #66133 |
| страница | 1 из 4 |
| Подборка по базе: Биология тема 13.docx, КР Моделирование.docx, 4 тема.docx, ВКР тема 7.docx, 6 Тема занятия «Практикум по разработке учебных заданий для форм, LAB моделирование роботов.docx, Военная топография Тема 1 Занятие 1.docx, уэф тема 2.pptx, Задания для практического занятия. Тема 2.pdf, Представлен основной учебный материал по темам.docx 1. Ошибки спецификации эконометрической модели имеют место вследствие … неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора 3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является … 4. В модели вида 5. При идентификации модели множественной регрессии Тема 2: Отбор факторов, включаемых в модель множественной регрессии 1. В модели множественной регрессии 2. При моделировании линейного уравнения множественной регрессии вида 3. Дана матрица парных коэффициентов корреляции.
и 5. Для эконометрической модели линейного уравнения множественной регрессии вида
Тема 3: Фиктивные переменные 1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать … использовать фиктивную переменную – пол потребителя разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола 3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: для типа дома кирпичный для типа дома монолитный для типа дома кирпичный для типа дома монолитный Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: 4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии: Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
Итоговое уравнение будет 5. В эконометрике фиктивной переменной принято считать … переменную, принимающую значения 0 и 1 Тема 4: Линейное уравнение множественной регрессии 1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение 2. В уравнении линейной множественной регрессии: на 1 тыс. руб. … увеличится на 10,8 тыс. руб. 4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы. Тема 5: Оценка параметров линейных уравнений регрессии 1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением. 3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует … 4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет … 0,2 минимизации суммы квадратов 1. Для обнаружения автокорреляции в остатках используется … статистика Дарбина – Уотсона критерий Гольдфельда – Квандта 2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что … автокорреляция остатков отсутствует 3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле 4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков. 5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК 1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством … 2. Из несмещенности оценки параметра следует, что среднее значение остатков равно … 3. Несмещенность оценок параметров регрессии означает, что … 4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков. нулевой средней величине точность оценок выборки увеличивается с увеличением объема выборки 1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками. автокоррелированными и/или гетероскедастичными 2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов. 3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда 4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если … средняя величина остатков не равна нулю 5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении 1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной … 2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является … 3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии 4. Для регрессионной модели вида получена диаграмма
Тема 10: Оценка качества подбора уравнения 1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно … 0,9 3. Для регрессионной модели вида , где остаточной дисперсии 🔍 ВидеоЭконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать  Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать  Множественная регрессияСкачать  Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать  Коэффициент детерминации. Основы эконометрикиСкачать  Эконометрика. Множественная регрессия и корреляция.Скачать  Эконометрика Линейная регрессия и корреляцияСкачать  Эконометрика. Неделя 1. Суть метода наименьших квадратов.Скачать  СЛММ Семерикова Е.В. Последствия ошибок спецификации пространственно-эконометрических моделейСкачать  Метод наименьших квадратов. Линейная аппроксимацияСкачать  Множественная регрессия в Excel и мультиколлинеарностьСкачать  МЕТРИКИ РЕГРЕССИИ В МАШИННОМ ОБУЧЕНИИ | MAE, MSE, RMSE, R2, коэффициент детерминации.Скачать  Видеоурок по эконометрике в Gretl. RESET-тест Рамсея, тест ЧоуСкачать  Определение эндогенностиСкачать  Парная регрессия: линейная зависимостьСкачать  |
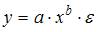
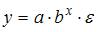
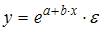
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
количество объясняющих переменных равно …
количество оцениваемых параметров равно …
определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
Коллинеарными являются факторы …
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х (1) , х (2) , х (3) , x (4) – независимые переменные):
Фиктивными переменными не являются …
,
, 
или 
для Республики Марий Эл;
для Республики Чувашия;
для Республики Татарстан.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
, где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
. Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
, где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
дисперсии остатков пропорциональны квадрату численности работников 
.После применения обобщенного метода наименьших квадратов новая модель приняла вид 
. Тогда параметр в новом уравнении характеризует среднее изменение затрат …
дисперсии остатков пропорциональны квадрату объема продукции 
.Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид 
. Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
, если известны парные коэффициенты корреляции , является интервал …
, а остаточная сумма квадратов отклонений, 
. Тогда значение коэффициента детерминации равно …
рассчитаны дисперсии: 
; 
; 
. Тогда величина 
характеризует долю …
, и остаточная сумма квадратов отклонений