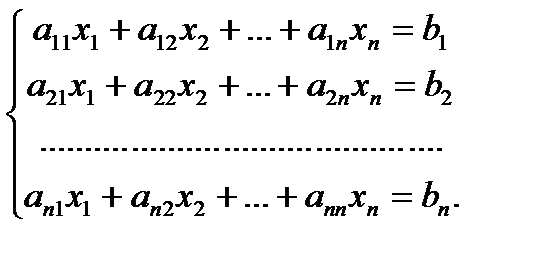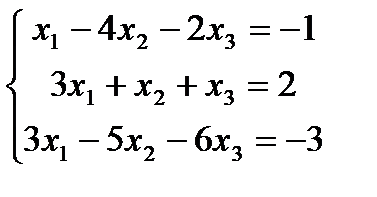Содержание:
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- Найдем определитель матрицы коэффициентов системы
- Определитель матрицы коэффициентов системы уравнений
- 💥 Видео
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:Решение системы уравнений методом Крамера.Скачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Матричный метод решения систем уравненийСкачать

Найдем определитель матрицы коэффициентов системы
Тема 6. Системы линейных алгебраических уравнений
Основные понятия СЛАУ
Системой состоящей из m линейных уравнений с n неизвестными называется система вида

где 
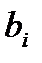

Решением линейной системы (1) называется упорядоченная совокупность чисел 
Линейная система называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все свободные члены равны нулю, то линейная система называется однородной. Однородная система имеет вид
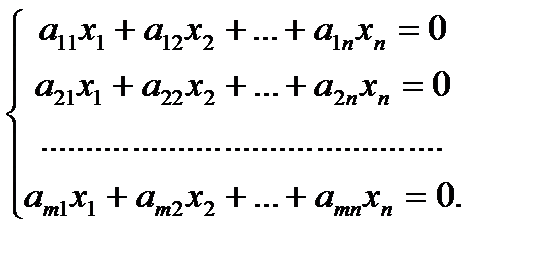
Система, имеющая хотя бы одно решение, называется совместной, а система не имеющая решений, — несовместной. Отметим, что однородная система всегда совместна, так как она имеет нулевое решение.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения.
Две системы называются эквивалентными или равносильными, если любое решение одной из них является так же решением другой и обратно, т.е. если имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.
Элементарными преобразованиями системы называются следующие преобразования:
1) умножение уравнения системы на число, отличное от нуля;
2) прибавление к одному уравнению системы другого ее уравнения, умноженного на любое число;
3) перестановка местами двух уравнений системы.
Определителем системы называется определитель матрицы А из коэффициентов уравнений этой системы
Матрица 
Решение СЛАУ по формулам Крамера
Пусть дана система n линейных уравнений с n неизвестными.
Обозначим через D определитель системы, а через Dk определитель, полученный заменой в определителе D столбца из коэффициентов при неизвестной хk столбцом свободных членов системы, т.е.
где k – одно из чисел 1, 2, …, n.
Теорема.
1) Если 


2) Если 

3) Если 
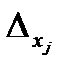

Пример. Решить систему линейных уравнений по формулам Крамера:
Решение:
Найдем определитель матрицы коэффициентов системы
Так как Δ # 0, то заданная система уравнений имеет единственное решение. Для этого вычислим определители Δj, получающиеся из определителя Δ путем замены в нем столбца, состоящего из коэффициентов при хj, столбцом свободных членов.

Ответ:
Примеры:
1. Рассмотрим систему 

Отсюда
2. 

Следовательно, система не имеет единственного решения. Найдем 
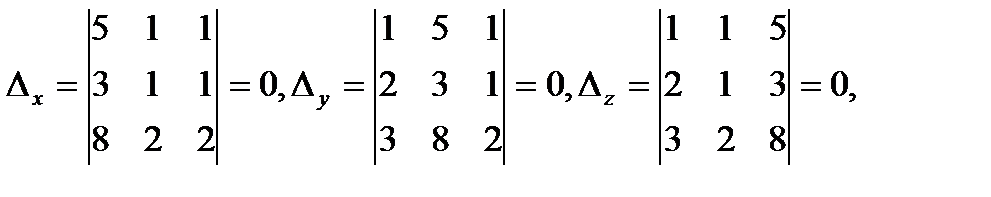
3. 

Видео:Решение системы уравнений методом ГауссаСкачать

Определитель матрицы коэффициентов системы уравнений
Дадим ряд необходимых определений.
Система линейных уравнений называется неоднородной, если хотя бы один ее свободный член отличен от нуля, и однородной, если все ее свободные члены равны нулю.
Решением системы уравнений называется упорядоченный набор чисел, который, будучи подставленным вместо переменных в систему, обращает каждое ее уравнение в тождество.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Рассмотрим неоднородную систему линейных алгебраических уравнений, имеющую при n = m следующий общий вид:
Главной матрицей A системы линейных алгебраических уравнений называется матрица, составленная из коэффициентов, стоящих при неизвестных:
Определитель главной матрицы системы называется главным определителем и обозначается ∆.
Вспомогательный определитель ∆ i получается из главного определителя путем замены i -го столбца на столбец свободных членов 
Теорема 1.1 (теорема Крамера). Если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, вычисляемое по формулам:
Если главный определитель ∆=0, то система либо имеет бесконечное множество решений (при всех нулевых вспомогательных определителях), либо вообще решения не имеет (при отличии от нуля хотя бы одного из вспомогательных определителей).
В свете приведенных выше определений , теорема Крамера может быть сформулирована иначе: если главный определитель системы линейных алгебраических уравнений отличен от нуля, то система является совместной определенной и при этом 
После этого следует провести проверку полученного решения.
Пример 1.4. Решить систему методом Крамера
Решение. Так как главный определитель системы
отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители
Воспользуемся формулами Крамера (1.6):
Пример 1.5. Данные дневной выручки молочного цеха от реализации молока, сливочного масла и творога за три дня продаж (на 2017 год) занесены в таблицу 1.4.
Определить стоимость 1 единицы продукции молокоцеха каждого вида.
Решение. Обозначим через x – стоимость 1 литра молока, y – 1 кг сливочного масла, z – 1 кг творога. Тогда, учитывая данные таблицы 1.4, выручку молочного цеха каждого из трех дней реализации можно отобразить следующей системой:
Решим систему методом Крамера. Найдем главный определитель системы по формуле (1.2):
Так как он отличен от нуля, то система имеет единственное решение. Вычислим вспомогательные определители с помощью формулы (1.2):
По формулам Крамера (1.6) имеем:
Вернувшись к обозначениям, видим, что стоимость 1 литра молока равна 44 рубля, 1 кг масла – 540 рублей, 1 кг творога – 176 рублей
Примечание. Как видно, процесс вычисления определителей вручную с помощью калькулятора трудоемок, поэтому на практике используют персональный компьютер. Так, для решения систем линейных алгебраических уравнений методом Крамера в MS Excel высчитывают ее главный и вспомогательные определители с использованием функции МОПРЕД( ), где аргументом является диапазон ячеек и элементы матрицы, определитель которой находится.
В MathCAD для нахождения определителя пользуются палитрой оператора Matrix
💥 Видео
Решение системы уравнений методом Крамера 2x2Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Решение системы уравнений методом Крамера 4x4Скачать

Линейная алгебра, 3 урок, ОпределителиСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

10. Метод Крамера решения систем линейных уравнений.Скачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Решение системы трех уравнений по формулам КрамераСкачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать







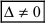 ), то система имеет единственное решение;
), то система имеет единственное решение;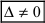 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 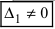 или
или 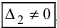 , или, . или
, или, . или 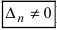 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);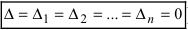 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.