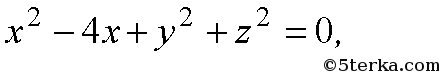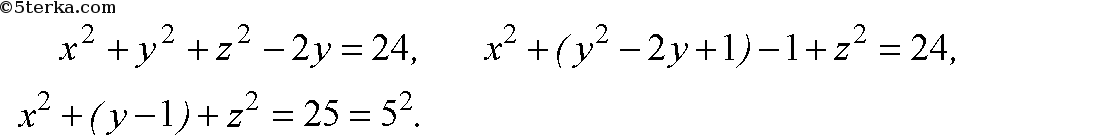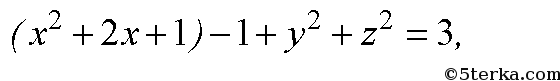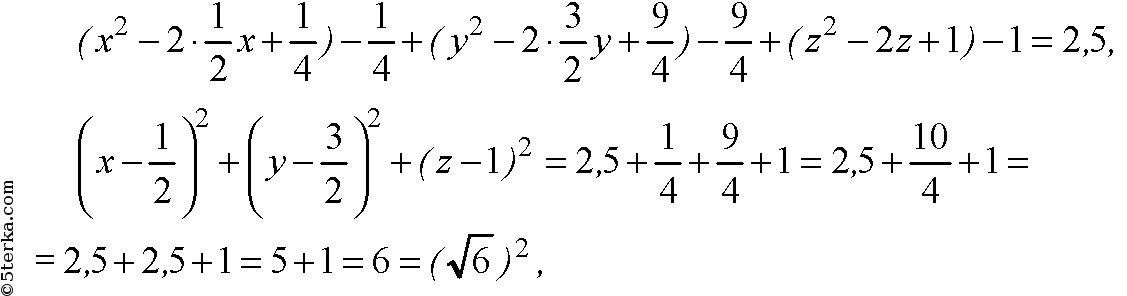- 579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координаты центра и радиус этой сферы: а) х2 —4x + y2 + z2 =0; б) x2+y2+z2—2y= 24; в) х2+ 2х + у2+z2 = 3; г) х2 — х — y2 + 3y + z2 —2z = 2,5.
- 579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координаты центра и радиус этой сферы: а) х 2 —4x + y 2 + z 2 =0; б) x 2 +y 2 +z 2 —2y= 24; в) х 2 + 2х + у 2 +z 2 = 3; г) х 2 — х — y 2 + 3y + z 2 —2z = 2,5.
- Основные методы решения уравнений в целых числах
- Докажите, что данное уравнение является уравнением сферы х ^ 2 + у ^ 2 + z ^ 2 + 2x — 2y = 2?
- Вершина А прямоугольника ABCD является центром окружности радиуса АB ?
- Прошу, помогите с геометрией?
- Напишите уравнения сферы R с центром А, если а (0, 0, 0 ) R = 3в кадрате?
- Напишите уравнение сферы радиуса R с центром А, если А(2 ; — 4 ; 7), R = 3?
- Даны точки А(3 ; 1) и В( — 5 ; 7) 1)Запишите уравнение окружности , диаметром которой является отрезок АВ ?
- Cфера задана уравнением (x — 1) ^ 2 + y ^ 2 + (z — 2) ^ 2 = 9 a) Назовите координаты цернтра и радиус сферы?
- Сфера задана уравнением Х ^ 2 + У ^ 2 + Z ^ 2 — 2y — 4z = 4 А) найти координаты центра и радиус сферы?
- Дана окружность с диаметрами AB и CD?
- Принадлежит ли точка М(3 ; 2 ; — 1) сфере, уравнение которой ?
- Помогите пожалуйста?
- 💥 Видео
Видео:11 класс, 20 урок, Уравнение сферыСкачать
579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координаты центра и радиус этой сферы: а) х2 —4x + y2 + z2 =0; б) x2+y2+z2—2y= 24; в) х2+ 2х + у2+z2 = 3; г) х2 — х — y2 + 3y + z2 —2z = 2,5.
Видео:№579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координатыСкачать
579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координаты центра и радиус этой сферы: а) х 2 —4x + y 2 + z 2 =0; б) x 2 +y 2 +z 2 —2y= 24; в) х 2 + 2х + у 2 +z 2 = 3; г) х 2 — х — y 2 + 3y + z 2 —2z = 2,5.
Координаты центра (2; 0; 0), радиус: 2;
Координаты центра (0; 1; 0), радиус: 5;
— уравнение сферы с центром (01; 0; 0), радиус: 2;
— уравнение сферы; в точке с координатами
расположен ее центр, радиус равен √6.
Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №579
к главе «Глава VI. Цилиндр, конус и шар § 3. Сфера».
Видео:№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать
Основные методы решения уравнений в целых числах
Введение
Существует множество математических задач, ответами к которым служат одно или несколько целых чисел. В качестве примера можно привести четыре классические задачи, решаемые в целых числах – задача о взвешивании, задача о разбиении числа, задача о размене и задача о четырёх квадратах. Стоит отметить, что, несмотря на достаточно простую формулировку этих задач, решаются они весьма сложно, с применением аппарата математического анализа и комбинаторики. Идеи решения первых двух задач принадлежат швейцарскому математику Леонарду Эйлеру (1707–1783). Однако наиболее часто можно встретить задачи, в которых предлагается решить уравнение в целых (или в натуральных) числах. Некоторые из таких уравнений довольно легко решаются методом подбора, но при этом возникает серьёзная проблема – необходимо доказать, что все решения данного уравнения исчерпываются подобранными (то есть решений, отличных от подобранных, не существует). Для этого могут потребоваться самые разнообразные приёмы, как стандартные, так и искусственные. Анализ дополнительной математической литературы показывает, что подобные задания достаточно часто встречаются в олимпиадах по математике разных лет и различных уровней, а также в задании 19 ЕГЭ по математике (профильный уровень). В то же время в школьном курсе математики данная тема практически не рассматривается, поэтому школьники, участвуя в математических олимпиадах или сдавая профильный ЕГЭ по математике, обычно сталкиваются со значительными трудностями при выполнении подобного рода заданий. В связи с этим целесообразно выделить систему основных методов решения уравнений в целых числах, тем более что в изученной математической литературе этот вопрос явно не оговаривается. Описанная проблема определила цель данной работы: выделить основные методы решения уравнений в целых числах. Для достижения поставленной цели необходимо было решить следующие задачи:
1) Проанализировать олимпиадные материалы, а также материалы профильного ЕГЭ по математике;
2) Обозначить методы решения уравнений в целых числах и выделить преобладающие;
3) Полученные результаты проиллюстрировать примерами;
4) Составить несколько тренировочных заданий по данной теме;
5) Применяя разработанные задания, определить степень готовности учащихся девятых классов МБОУ СОШ №59 к решению подобного рода задач и сделать практические выводы.
Основная часть
Анализ разнообразной математической литературы показывает, что среди методов решения уравнений в целых числах в качестве основных можно выделить следующие:
- Представление уравнения в виде произведения нескольких множителей, равного некоторому целому числу;
- Представление уравнения в виде суммы квадратов нескольких слагаемых, равной некоторому целому числу;
- Использование свойств делимости, факториалов и точных квадратов;
- Использование Малой и Великой теорем Ферма;
- Метод бесконечного спуска;
- Выражение одной неизвестной через другую;
- Решение уравнения как квадратного относительно одной из неизвестных;
- Рассмотрение остатков от деления обеих частей уравнения на некоторое число.
Сразу же нужно оговорить, что мы понимаем под основными методами решения уравнений. Основными будем называть наиболее часто применяющиеся методы, что, конечно, не исключает возможности периодического применения новых «неожиданных» приёмов. Кроме того, причём в подавляющем большинстве случаев, применяют их различные сочетания, то есть проводят комбинирование нескольких методов.
В качестве примера сочетания методов рассмотрим уравнение, предлагавшееся на ЕГЭ по математике в 2013 году (задание С6).
Задача. Решить в натуральных числах уравнение n! + 5n + 13 = k 2 .
Решение. Заметим, что оканчивается нулём при n > 4. Далее, при любых n ∈ N оканчивается либо цифрой 0, либо цифрой 5. Следовательно, при n > 4 левая часть уравнения оканчивается либо цифрой 3, либо цифрой 8. Но она же равна точному квадрату, который не может оканчиваться этими цифрами. Поэтому нужно перебрать только четыре варианта: n = 1, n = 2, n = 3, n = 4.
Значит, уравнение имеет единственное натуральное решение n = 2, k = 5.
В этой задаче использовались свойства точных квадратов, свойства факториалов, и остатки от деления обеих частей уравнения на 10.
Теперь приведём комплекс авторских задач.
Задача 1. Решить в целых числах уравнение n 2 — 4y! = 3.
Решение. Сначала перепишем исходное уравнение в виде n 2 = 4y! + 3. Если посмотреть на это соотношение с точки зрения теоремы о делении с остатком, то можно заметить, что точный квадрат, стоящий в левой части уравнения, даёт при делении на 4 остаток 3, что невозможно. Действительно, любое целое число представимо в одном из следующих четырёх видов:
Таким образом, точный квадрат при делении на 4 даёт в остатке либо 0, либо 1. Следовательно, исходное уравнение не имеет решений.
Ключевая идея – применение свойств точных квадратов.
Задача 2. Решить в целых числах уравнение 8z 2 = (t!) 2 + 2.
Решение. Непосредственная проверка показывает, что t = 0 и t = 1 не являются решениями уравнения. Если t > 1, то t! является чётным числом, то есть, оно представимо в виде t! = 2s. В таком случае уравнение можно преобразовать к виду 4z 2 = 2s 2 + 1. Однако, полученное уравнение заведомо не имеет решений, ибо в левой части стоит чётное число, а в правой – нечётное.
Ключевая идея – применение свойств факториалов.
Задача 3. Решить в целых числах уравнение x 2 + y 2 – 2x + 6y + 5 = 0.
Решение. Исходное уравнение можно переписать следующим образом: (x – 1) 2 + (y + 3) 2 = 5.
Из условия следует, что (x – 1), (y + 3) – целые числа. Следовательно, данное уравнение эквивалентно следующей совокупности:
Теперь можно выписать всевозможные целые решения уравнения.
Задача 4. Решить в целых числах уравнение zt + t – 2z = 7.
Решение. Исходное уравнение можно преобразовать к виду (z + 1) (t – 2) = 5. Числа (z + 1), (t – 2) являются целыми, поэтому имеют место следующие варианты:
Итак, уравнение имеет ровно четыре целых решения.
Ключевая идея – представление уравнения в виде произведения, равного целому числу.
Задача 5. Решить в целых числах уравнение n(n + 1) = (2k + 1)‼
Решение. Число (2k + 1)‼ нечётно при всех неотрицательных значениях k согласно определению (при отрицательных k оно вообще не определено). С другой стороны, оно равно числу n(n + 1), которое чётно при всех целых значениях k. Противоречие.
Ключевая идея – использование чётности/нечётности частей уравнения.
Задача 6. Решить в целых числах уравнение xy + x + 2y = 1.
Решение. Путём преобразований уравнение можно свести к следующему:
Данное преобразование не изменило ОДЗ неизвестных, входящих в уравнение, так как подстановка y = –1 в первоначальное уравнение приводит к абсурдному равенству –2 = 1. Согласно условию, x – целое число. Иначе говоря, 
тоже целое число. Но тогда число 
обязано быть целым. Дробь является целым числом тогда и только тогда, когда числитель делится на знаменатель. Делители числа 3: 1,3 –1, –3. Следовательно, для неизвестной возможны четыре случая: y = 0, y = 2, y = –2, y = –4. Теперь можно вычислить соответствующие значения неизвестной x. Итак, уравнение имеет ровно четыре целых решения: (–5;0), (–5;2), (1;–2), (1;–4).
Ключевая идея – выражение одной неизвестной через другую.
Задача 7. Решить в целых числах уравнение 5 m = n 2 + 2.
Решение. Если m = 0, то уравнение примет вид n 2 = –1. Оно не имеет целых решений. Если m 0. Тогда правая часть уравнения (как и левая) будет кратна 5. Но в таком случае n 2 при делении на 5 должно давать остаток 3, что невозможно (это доказывается методом перебора остатков, который был изложен при решении задачи 1). Следовательно, данное уравнение не имеет решений в целых числах.
Ключевая идея – нахождение остатков от деления обеих частей уравнения на некоторое натуральное число.
Задача 8. Решить в целых числах уравнение (x!) 4 + (y – 1) 4 = (z + 1) 4 .
Решение. Заметим, что в силу чётности показателей степеней уравнение эквивалентно следующему: (x!) 4 + |y – 1| 4 = |z + 1| 4 . Тогда x!, |y – 1|, |z + 1| – натуральные числа. Однако, согласно Великой теореме Ферма, эти натуральные числа не могут удовлетворять исходному уравнению. Таким образом, уравнение неразрешимо в целых числах.
Ключевая идея – использование Великой теоремы Ферма.
Задача 9. Решить в целых числах уравнение x 2 + 4y 2 = 16xy.
Решение. Из условия задачи следует, что x – чётное число. Тогда x 2 = 4x1 2 . Уравнение преобразуется к виду x1 2 + y 2 = 8x1y. Отсюда вытекает, что числа x1, y имеют одинаковую чётность. Рассмотрим два случая.
1 случай. Пусть x1, y – нечётные числа. Тогда x1 = 2t + 1, y = 2s + 1. Подставляя эти выражения в уравнение, получим:
Выполним соответствующие преобразования:
Сокращая обе части полученного уравнения на 2, получим?
В левой части стоит нечётное число, а в правой – чётное. Противоречие. Значит, 1 случай невозможен.
2 случай. Пусть x1, y – чётные числа. Тогда x1 = 2x2 + 1, y = 2y1. Подставляя эти значения в уравнение, получим:
Таким образом, получилось уравнение, точно такое же, как на предыдущем шаге. Исследуется оно аналогично, поэтому на следующем шаге получим уравнение 
и т.д. Фактически, проводя эти преобразования, опирающиеся на чётность неизвестных, мы получаем следующие разложения: 
. Но величины n и k не ограничены, так как на любом шаге (со сколь угодно большим номером) будем получать уравнение, эквивалентное предыдущему. То есть, данный процесс не может прекратиться. Другими словами, числа x, y бесконечно много раз делятся на 2. Но это имеет место, только при условии, что x = y = 0. Итак, уравнение имеет ровно одно целое решение (0; 0).
Ключевая идея – использование метода бесконечного спуска.
Задача 10. Решить в целых числах уравнение 5x 2 – 3xy + y 2 = 4.
Решение. Перепишем данное уравнение в виде 5x 2 – (3x)y + (y 2 – 4) = 0. Его можно рассмотреть как квадратное относительно неизвестной x. Вычислим дискриминант этого уравнения:
Для того чтобы уравнение имело решения, необходимо и достаточно, чтобы 
, то есть 
Отсюда имеем следующие возможности для y: y = 0, y = 1, y = –1, y = 2, y = –2.
Итак, уравнение имеет ровно 2 целых решения: (0;2), (0;–2).
Ключевая идея – рассмотрение уравнения как квадратного относительно одной из неизвестных.
Составленные автором задачи были использованы при проведении эксперимента, который состоял в следующем. Всем учащимся девятых классов были предложены разработанные задания с целью выявления уровня подготовки детей по данной теме. Каждому из учеников необходимо было предложить метод нахождения целочисленных решений уравнений. В эксперименте приняли участие 64 ученика. Полученные результаты представлены в таблице 1.
ТАБЛИЦА 1
| Номер задания |
