- Условие
- Решение
- Определите взаимное расположение прямых задаваемых уравнениями x 1 2t y 1 t z 1 3t
- Точка пересечения прямых в пространстве онлайн
- Предупреждение
- Точка пересечения прямых в пространстве − теория, примеры и решения
- 1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
- 2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
- 3. Точка пересечения прямых в пространстве, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
- Математический портал
- Nav view search
- Navigation
- Search
- Прямая в пространстве, всевозможные уравнения.
- 🔍 Видео
Условие
Определить взаимное расположение двух прямых в пространстве, если даны :
a: x=1+t, y=-2-2t, z=3-2t
b: x=t, y=1-3t, z=1+2t
Решение
(x-1)=(y+2)/(-2)=(z-3)/(-2) — прямая проходит через точку M_(1)(1;-2;3) и
направляющий вектор прямой а:
vector=(1;-2;-2)
b:
x=t ⇒ t=x
y=1–3t ⇒ t=(y-1)/(-3)
z=1+2t ⇒ t=(z-1)/2-прямая проходит через точку M_(2)(0;1;1) и
направляющий вектор прямой b:
vector(1;-3;2)
Направляющие векторы не коллинеарны ⇒ прямые не параллельны и не совпадают
Проверяем принадлежат лежат ли прямые а и b одной плоскости.
[m]begin -1&3&-2\1&-2&-2\1&-3&2end =0[/m], так как первая и вторая строки пропорциональны
Прямые лежат в одной плоскости ⇒ так как они не параллельны, значит пересекаются.
Видео:15. Взаимное расположение прямых в пространствеСкачать

Определите взаимное расположение прямых задаваемых уравнениями x 1 2t y 1 t z 1 3t
1.Знать уравнения прямой и уравнения плоскости, формулы вычисления угла между прямыми, между прямой и плоскостью, между плоскостями; формулы вычисления расстояния от точки до прямой и от точки до плоскости.
2.Уметь применять данные знания при решении задач, пояснять решения, отстаивать свою точку зрения, опираясь на отличное знание теории, работать в группе, проявлять активность и творчество.
3.Обеспечить в ходе урока воспитание целеустремленности, настойчивости, коммуникативных качеств личности, ораторских способностей и чувства времени.
Оборудование, наглядные пособия : ПК учащихся, интерактивная доска, инструмент доски, сканер, доска, мел, раздаточный материал, листы А3, по два на каждую группу.
Тип урока: Урок комплексного применения знаний и способов деятельности.
Цель урока : Усвоение умений самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.
Методы и формы: КСО, элементы проблемного обучения, групповая работа, деловая игра «Рынок возможностей»
I . Организационный момент. Презентация 1,слайды -1, 2. — 3мин
II . Актуализация знаний и способов деятельности, необходимых для творческого применения. Проверка домашнего задания. Проверка знаний: «Лови ошибку! » — 4 мин. Презентация 1, слайды 3-5.
III . Обобщение и систематизация знаний и способов деятельности
«Презентация знаний » — 9мин.
IV . Применение обобщенных знаний и умений в новых условиях.
« Знания в дело!» Презентация 1, слайды 6-9. -5мин.
V . Освоение образца комплексного применения знаний и умений.
«Путь к вершине знаний» Презентация 1, слайды 10-12— 10 мин.
VI Комплексное применение знаний и умений.
«Путь к вершине успеха» Презентация 1, слайды 13-15-10мин
Подведение итогов урока. Рефлексия-3мин.
VIII Задание на дом.
Информация о домашнем задании.-1мин.
I . Организационный момент.
« Добрый день, господа! Рада Вас видеть и предлагаю начать работу по применению знаний по теме: «Взаимное расположение прямых и плоскостей в координатах». На доске Презентация 1. – Название темы урока.
Успехов вам и хорошего настроения!»
Вам предлагается «Рынок возможностей» по применению рассмотренных ранее уравнений прямой и плоскости и их взаимного расположения в координатах.
В конкурсе принимают участие три группы предпринимателей, которым предстоит пройти лестницу к вершине успеха.
«Путь к вершине знаний»
«Путь к вершине успеха»
На первой ступени испытание- «Лови ошибку!», на второй – «Презентация знаний» по теме, которая вам достанется по жребию, на третьей – три испытания: «Знания в дело!», « Путь к вершине знаний», « Путь к вершине успеха». Вершины достигает группа, набравшая максимальное число баллов.
Завершающий этап – инструктаж: «Как удержаться на вершине успеха».
II . Актуализация знаний и способов деятельности, необходимых для творческого применения. Проверка домашнего задания. Проверка знаний: «Лови ошибку! ». На обсуждение в группе 1 мин, на защиту решения – 3 мин (по 1 мин каждой команде). По одному представителю от каждой команды, после обсуждения в группе выходят к доске и исправляют ошибки.
Цена задания – 3 балла. Цена дополнения – 1 балл (снимается со счета команды, если другая команда сделала существенное дополнение).
На ПК учащихся и 3-5слайдах – задания с ошибкой. Повторение и закрепление уравнения прямой и плоскости.
1. Уравнение плоскости, проходящей через точку М (2; 1; -2) перпендикулярно вектору n4; -5; 7, имеет вид: 2( x — 4) + 1( y + 5) — 2( z – 7) = 0.
2. Уравнение прямой, проходящей через точку М (2; 3; -1), параллельно вектору p4; 7; -2, имеет вид: .
3. Прямая, проходящая через точку М (0; 2; 4), параллельная вектору p-3; 0; 5, имеет вид: x =-3 t , y = t +2, z =4+5 t .
III . Обобщение и систематизация знаний и способов деятельности
«Презентация знаний » -9мин.
От каждой группы выходит представитель и тянет жребий – название темы, по которой группа будет делать свой мини-проект. Мини-проект выполняется на 2 листах формата А3 в течение двух минут.
Доклад у доски – презентация конспекта темы занимает не более 2 минут, с учетом вопросов выступающим.
Требования к конспекту: краткость, наглядность, к каждому случаю чертеж, формула для вычисления угла, доступность, последовательность и четкость объяснения. Подведение итогов. Максимальное количество баллов – 5. Цена дополнения – 1 балл (снимается с команды, если существенное дополнение).
IV . Применение обобщенных знаний и умений в новых условиях.
« Знания в дело!». Путь к вершине – результат удачного применения знаний. Нарушение регламента – минус 1 балл. После каждого этапа IV – VI — подведение итогов. Задачи решаются на интерактивной доске (защита решений). На доклад по каждой задаче уровня А по 0,5 мин, уровня В по 1мин, на задачи уровня С по 2,5 мин. Докладчик представляет краткие записи плана решения с устными пояснениями к нему.
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
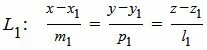 , , | (1) |
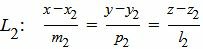 , , | (2) |
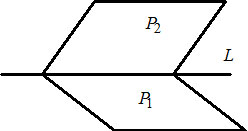
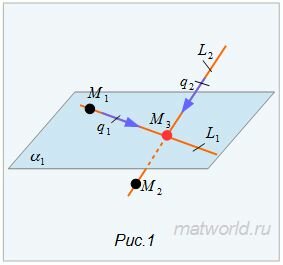
Найти точку пересечения прямых L1 и L2 (Рис.1).
 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
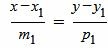 , , | (3) |
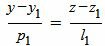 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
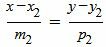 , , | (7) |
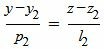 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
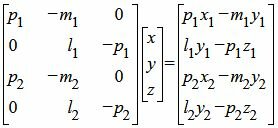 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
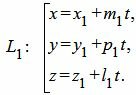 | (12) |
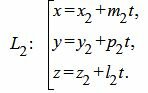 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
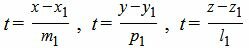 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
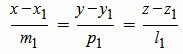 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
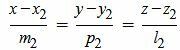 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
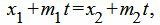 | (17) |
 | (18) |
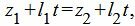 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
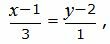 | (22) |
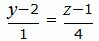 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
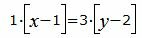 |
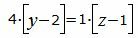 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
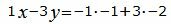 |
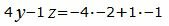 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
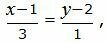 | (26) |
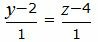 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
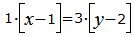 |
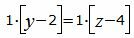 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
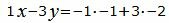 |
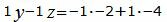 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
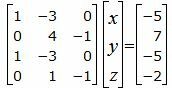 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
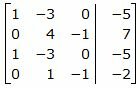 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
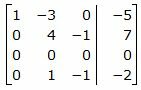 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
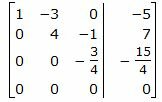 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
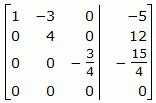 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
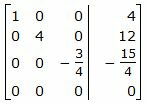 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
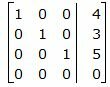 |
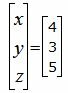 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
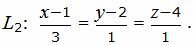 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
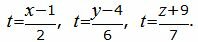 |
Из равентсв выше получим каноническое уравнение прямой:
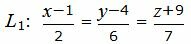 | (33) |
Представим уравнение (33) в виде двух уравнений:
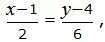 | (34) |
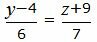 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
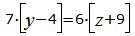 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
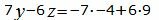 |
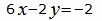 | (36) |
 . . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
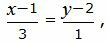 | (38) |
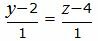 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
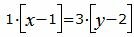 |
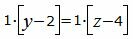 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
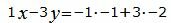 |
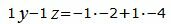 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
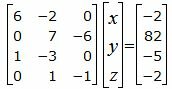 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
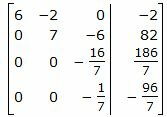 |
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
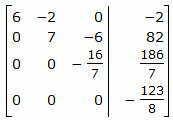 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
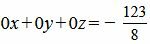 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=, а прямая L2 имеет направляющий вектор q2=. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
Видео:22. Взаимное расположение прямой и плоскости в пространствеСкачать

Математический портал
Видео:Лекция 2. Взаимное расположение прямых линий.Скачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Высшая математика.
- Аналитическая геометрия.
- Прямая в пространстве, всевозможные уравнения, взаимное расположение прямых в пространстве, расстояние от точки до прямой в пространстве.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Прямая в пространстве, всевозможные уравнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения прямой в пространстве:
1) $left<beginA_1x+B_1y+C_1z+D_1=0quad (P_1)\ A_2x+B_2y+C_2z+D_2=0quad (P_2)endright. — $ общее уравнение прямой $L$ в пространстве, как линии пересечения двух плоскостей $P_1$ и $P_2.$
2) $frac=frac=frac
-$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline=(m, n, p).$ Вектор $overline S$ является направляющим вектором прямой $L.$
3) $frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$
4) Приравнивая каждую из частей канонического уравнения 2 к прараметру $t,$ получаем параметрическое уравнение прямой:
Расположение двух прямых в пространстве.
Условие параллельности двух прямых: Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac=frac=frac
.$
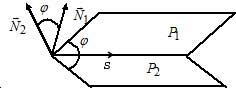
Условие перпендикулярности двух прямых: $L_1perp L_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot+cdot+p_1cdot p_2=0.$
Угол между прямыми:
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на данную прямую.
Пусть прямая $L$ задана уравнением $frac=frac=frac
,$ следовательно $overline S=(m, n, p).$ Пусть также $M_2=(x_2, y_2, z_2) -$ произвольная точка, принадлежащая прямой $L.$ Тогда расстояние от точки $M_1=(x_1, y_1, z_1)$ до прямой $L$ можно найти по формуле: $$d(M_1, L)=frac<|[overline, overline S]|>.$$
Примеры.
2.198. Написать каноническое уравнение прямой, проходящей через точку $M_0(2, 0, -3)$ параллельно:
а) вектору $q(2, -3, 5);$
е) прямой $x=-2+t, y=2t, z=1-fract.$
Решение.
а) Воспользуемся формулой (2) уравнения прямой в пространстве:
$frac=frac=frac
-$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline=(m, n, p).$
По условию $M_0(2, 0, -3)$ и $overline=q(2,-3,5).$
б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой $frac=frac=frac$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):
в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$
д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей , поэтому Направляющий вектор прямой
$left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ можно найти как векторное произведение нормалей заданных плоскостей.
Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$
для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$
Находим векторное произведение:
Таким образом, направляющий вектор прямой $left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ имеет координаты $overline S (-4, 8, 10).$
Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(-4, 8, 10):$
е) Найдем направляющий вектор прямой $x=-2+t, y=2t, z=1-fract.$ Для этого запишем уравнение этой прямой в каноническом виде:
Отсюда находим направляющий вектор $overline Sleft(1, 2, -fracright).$ Умножим координаты направляющего вектора на 2 (чтобы избавиться от дроби): $overline S_1(2, 4, -1).$
Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(2, 4, -1):$
2.199(a). Написать уравнение прямой, проходящей через две заданные точки $M_1 (1, -2, 1)$ и $M_2(3, 1, -1).$
Решение.
Воспользуемся формулой (3) уравнения прямой в пространстве:
$frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$
Подставляем заданные точки:
2.204. Найти расстояние между параллельными прямыми
Решение.
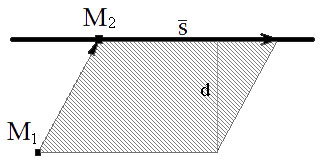
Расстояние между параллельными прямыми $L_1$ и $L_2$ равно расстоянию от произвольной точки прямой $L_1$ до прямой $L_2.$ Следовательно, его можно найти по формуле $$d(L_1, L_2)=d(M_1, L_2)=frac<|[overline, overline S]|>,$$ где $M_1-$ произвольная точка прямой $L_1,$ $M_2 — $произвольная точка прямой $L_2,$ $overline S -$ направляющий вектор прямой $L_2.$
Из канонических уравнений прямых берем точки $M_1=(2, -1, 0)in L_1,$ $M_2=(7, 1, 3)in L_2,$ $overline S=(3, 4, 2). $
Отсюда находим $overline=(7-2, 1-(-1),3-0)=(5, 2, 3);$
Ответ: 3.
2.205 (а). Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$
Решение.
Для того, чтобы найти расстояние от точки $A$ до прямой $L,$ нам необходимо выбрать произвольную точку $M,$ принадлежащую прямой $L$ и найти направляющий вектор этой прямой.
Выбираем точку $M.$ Пусть координата $z=0.$ Подставим это значение в данную систему:
Таким образом, $M=(-14, -frac, 0)$
Направляющий вектор найдем, как векторное произведение нормалей заданных плоскостей:
Для плоскости $P_1:$ $2x-2y+z+3=0$ нормальный вектор имеет координаты $N_1(2, -2, 1);$
для плосости $P_2:$ $3x+2y+2z+17=0,$ нормальный вектор имеет координаты $N_2(3, -2, 2).$
Находим векторное произведение:
Таким образом, направляющий вектор прямой $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$
имеет координаты $overline S (-2, -1, 2).$
Теперь можно воспользоваться формулой $$d(A, L)=frac<|[overline, overline S]|>.$$
$overline=left(2-(-14),3-left(-fracright),-1-0right)=left(16, 15frac, -1right)$
Ответ: $d(A, L)=15.$
2.212. Написать каноническое уравнение прямой, которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $P: 3x-2y-3z-7=0$ и пересекает прямую $L: frac=frac=frac.$
Решение.
Запишем уравнение плоскости $P_1,$ которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $3x-2y-3z-7=0:$
$P: 3x-2y-3z-7=0Rightarrow overline N=(3; -2; -3).$ Искомая плоскость проходит через точку $M_0(3, -2, -4)$ перпендикулярно вектору $overline N(3, -2, -3).$
$P_1: 3x-9-2y-4-3z-12=0 Rightarrow$
Далее найдем точку пересечения плоскости $P_1$ и прямой $L.$ Для этого запишем уравнение прямой $L$ в параметрической форме:
Далее, подставим значения $x, y$ и $z,$ выраженные через $t$ в уравнение плоскости $P_1,$ и из полученного уравнения выразм $t:$
Подставляя найденное занчение $t$ в уравнение прямой $L,$ найдем координаты точки пересечения:
Таким образом, прямая $L$ и плоскость $P_1$ пересекаются в точке $M_1(8, -8, 5).$
Теперь запишем уравнение прямой, проходящей через точки $M_0(3, -2. -4)$ и $M_1(8, -8, 5)$— это и будет искомая прямая. Воспользуемся формулой ( 3) $frac=frac=frac :$
2.199.
б) Написать уравнение прямой, проходящей через две заданные точки $M_1 (3, -1, 0)$ и $M_2(1, 0, -3).$
б) Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $ L:$ $left<beginx=3t+5,\ y=2t,\z=-2t-25. endright.$
2.206. Доказать, что прямые $L_1: left<begin2x+2y-z-10=0,\ x-y-z-22=0, endright.$ и $L_2: frac=frac=frac.$ параллельны и найти расстояние $rho(L_1, L_2)$
2.207. Составить уравнения прямой, проходящей через точки пересечения плоскости $x-3y+2z+1=0$ с прямыми $frac=frac=frac$ и $frac=frac=frac.$
2.211. Написать уравнение прямой, проходящей через точку $M_0(7, 1, 0)$ параллельно плоскости $2x+3y-z-15=0$ и пересекающей прямую $frac=frac=frac.$
🔍 Видео
Взаимное расположение прямых на плоскости. 7 класс.Скачать

Взаимное расположение прямых на плоскости. Практическая часть. 7 класс.Скачать

Решение задач. Плоскость в пространстве. Взаимное расположение плоскостей, уравнение "в отрезках".Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Взаимное расположение прямых в пространстве. Видеоурок 3. Геометрия 10 классСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Геометрия 10 класс (Урок№5 - Взаимное расположение прямых в пространстве.)Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Линал I Лекция 3. Прямая на плоскости. Взаимное расположение прямых. Плоскость.Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать