Определите по уравнению сферы координаты ее центра и радиус

Найдите координаты центра и радиус сферы, заданной уравнением: а) х 2 + у 2 + z 2 = 49; б) (х — 3) 2 + (у + 2) 2 + z ₂ = 2.

а) х 2 +у 2 + z 2 = 49.
(х-х₀) 2 +(у-y₀) 2 +(z-z₀) 2 = R 2 , где R — радиус сферы, (х₀;у₀;z₀)
— координаты точки С, центра сферы. В нашем случае
х-х₀ =х; у-у₀ =у: z-z₀ =z, поэтому х₀ = 0; у0 = 0, z₀=0. a R = √49 = 7. Координаты центра (0;0;0), радиус: 7.
б)(x-x₀) 2 +(y-y₀) 2 +x 2 =2
(x-x₀) 2 +(y-y₀) 2 +(z-z₀) 2 = R 2 , х-3 = х-х₀, х₀ =3;
у+2. = у-у₀, у₀ = -2; z-z₀=z, z_о=0; 2 = R 2 , R = √2
Координаты центра: (3;-2;0), радиус: √2.

Задача 29234 5.1.27. Найти координаты центра и радиус.

Условие

5.1.27. Найти координаты центра и радиус сферической поверхности,
заданной уравнением x^2+y^2+z^2-2x+6z-6=0

Решение

Нормальное уравнение сферы
(x-a)^2+(y-b)^2+(z-c)^2=R^2
c центром в точке (a;b;c) и радиусом R

Выделяем полные квадраты
(x^2-2x)+y^2+(z^2+6z)-6=0
(x^2-2x+1)+y^2+(x^2+6z+9)-1-9-6=0

О т в е т. (1;0;-3) — координаты центра; R=4

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

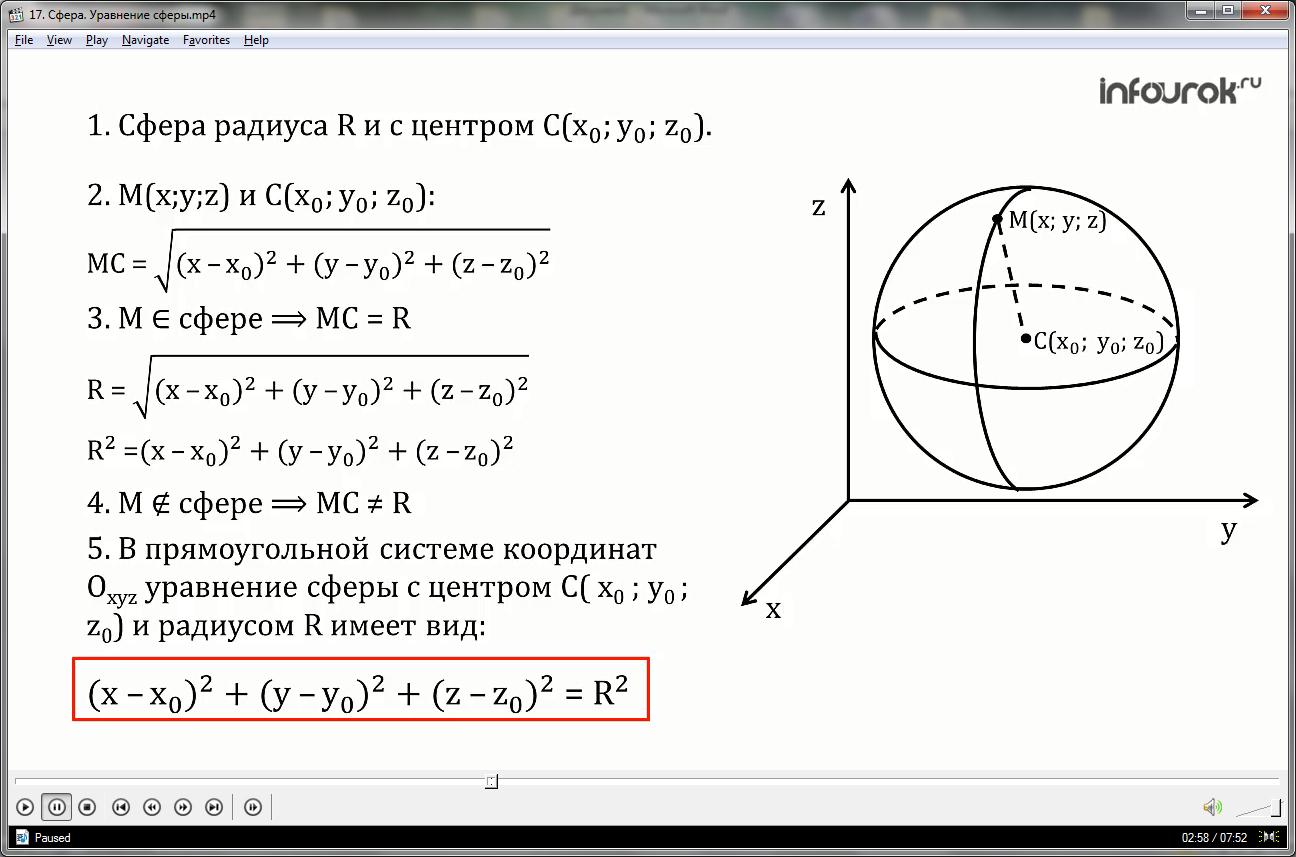
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

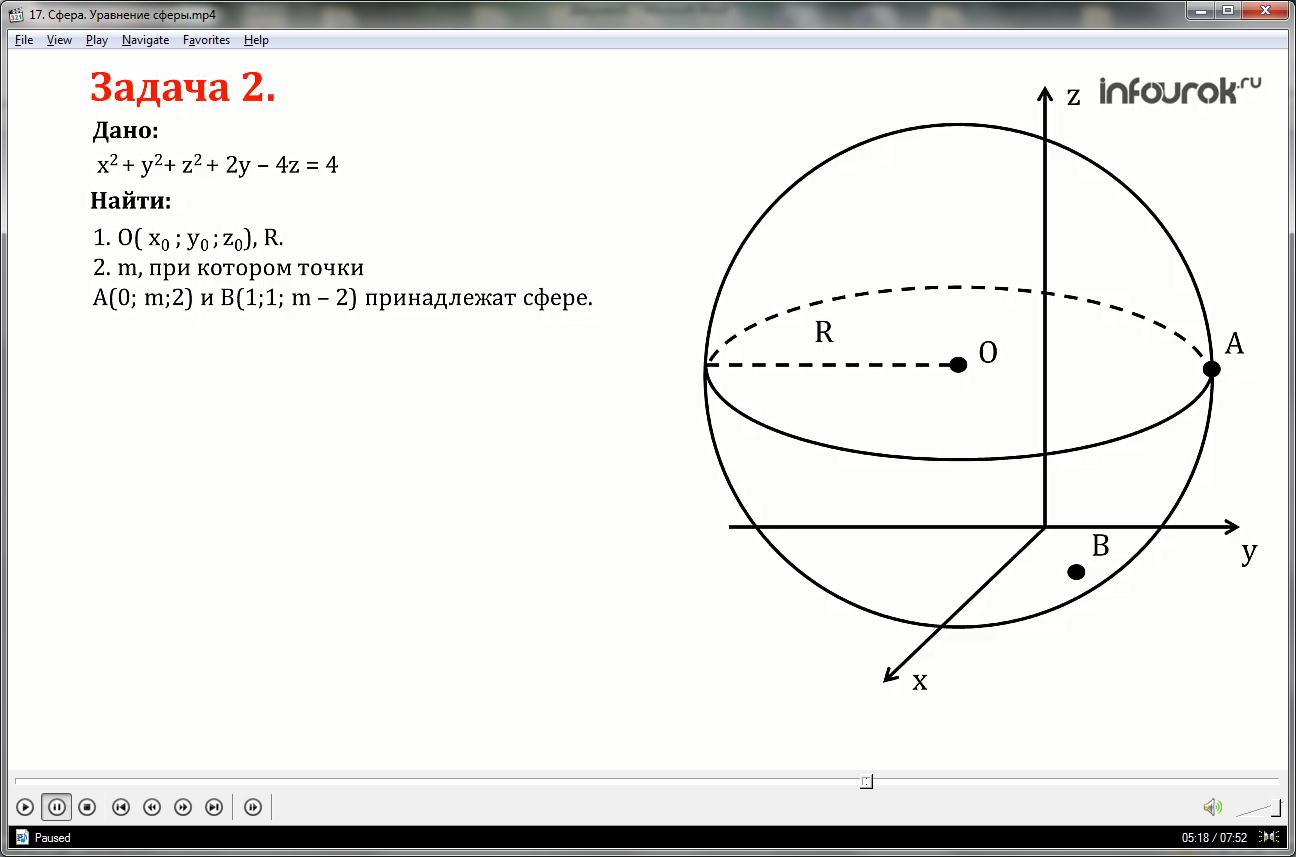
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

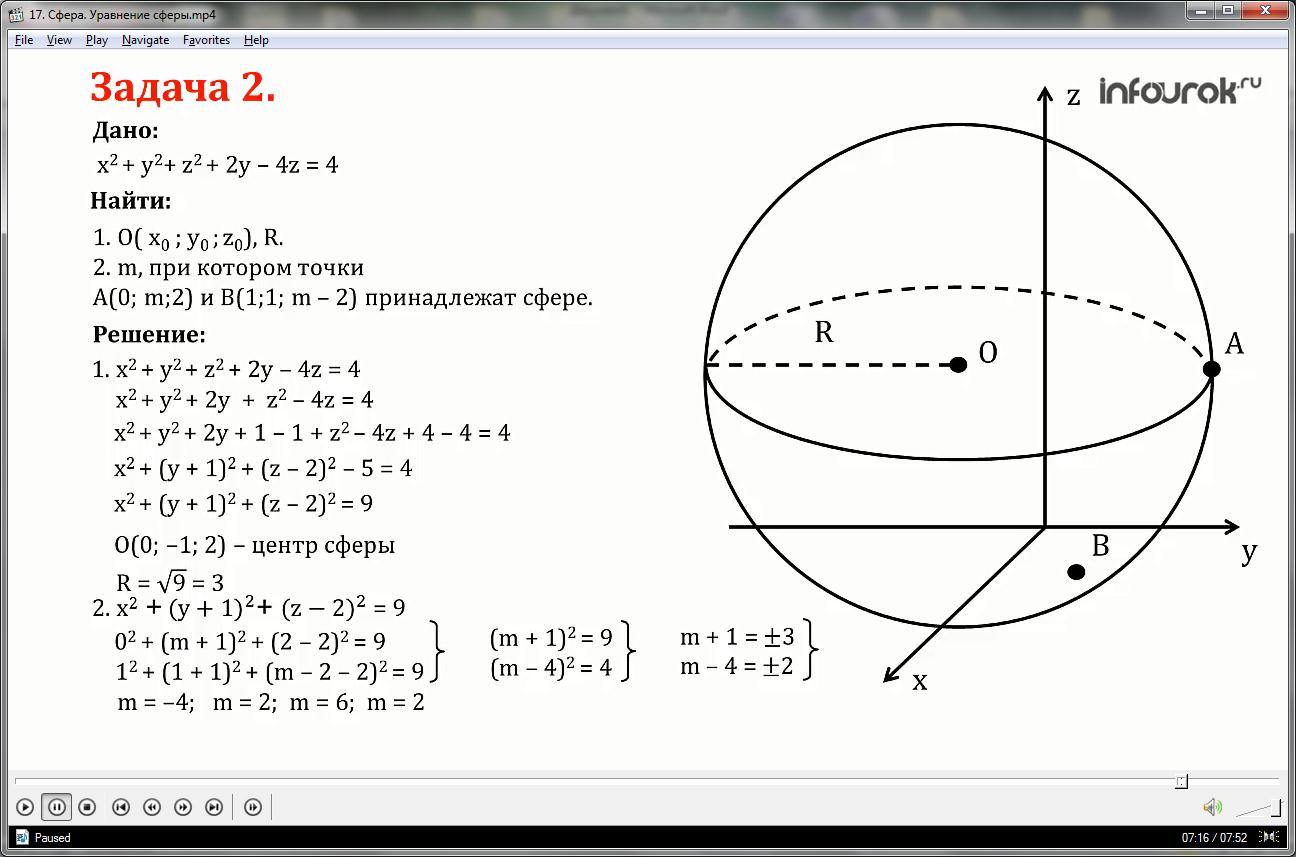
1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

53343

1003

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

🎦 Видео