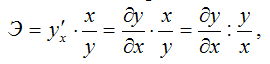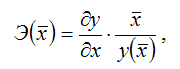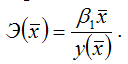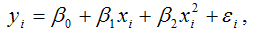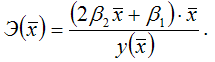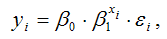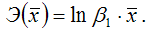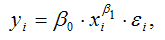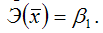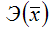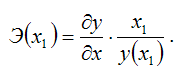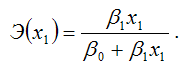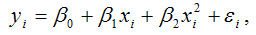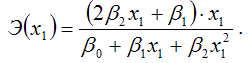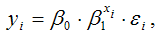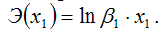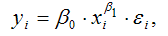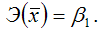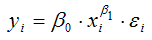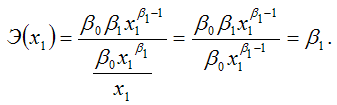Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле:

y’_x – первая производная результативной переменной у по факторной переменной x.

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня y если факторная переменная х изменится на 1 % относительного своего среднего уровня x Общая формула для расчёта коэффициента эластичности для среднего значения x факторной переменной х:

где y( x ) – значение функции у при среднем значении факторной переменной х.

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Это единственная нелинейная функция, для которой средний коэффициент эластичности

равен коэффициенту регрессии β₁.

Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х₁.

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х₁, если факторная переменная изменится на 1 % относительно заданного уровня х₁.

Общая формула для расчёта коэффициента эластичности для заданного значения х₁ факторной переменной х:

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение линейной функции в точке х₁.

Для полиномиальной функции второго порядка (параболической функции) вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение параболической функции в точке х₁.

Для показательной функции вида:

точечный коэффициент эластичности определяется по формуле:

Для степенной функции вида:

точечный коэффициент эластичности определяется по формуле:

Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

через первую производную результативной переменной по заданной факторной переменной x₁:

Следовательно, Э(x₁) = β₁, что и требовалось доказать.

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.

Раздел 1. Исходные основы микроэкономики

Практическая работа 2

Целью данного практикума является усвоение методики расчета коэффициентов эластичности и их применения на практике.

Задачами практикума являются:

• во-первых, приобретение навыков расчетов коэффициентов эластичности;
• во-вторых, использование коэффициентов эластичности для определения ценовой и производственной политики фирмы.

Оглавление

Задачи на расчет коэффициентов эластичности

Задача 1

Постановка задачи: Рассмотрите рисунок. Определите коэффициент ценовой эластичности на отрезке АВ кривой спроса d₁. О каком товаре идет речь?

Технология решения задачи: Для решения задачи необходимо вспомнить, как определяется дуговой коэффициент ценовой эластичности. Коэффициент эластичности обозначим Е_d/p, тогда

Поставив в формулу значения, получим:

Этот коэффициент характеризует эластичный товар.

Ответ: коэффициент эластичности равен –2,3. Товар эластичен.

Задача 2

Постановка задачи: Даны три товара. Изменения объемов спроса в зависимости от изменения цены приведены в таблице. Определите коэффициенты ценовой эластичности по каждому товару.

Товар А

Товар В

Товар С

Цена

Количество

Цена

Количество

Цена

Количество

Технология решения задачи: необходимо определить коэффициенты дуговой эластичности спроса по цене по каждому товару. Коэффициент эластичности товара А (Е_{d/p A}) определяется по формуле

Поставив в формулу значения, получим:

Этот коэффициент характеризует эластичный товар.

Аналогично рассчитаем коэффициент эластичности по товару В:

Задача 3

Постановка задачи: В результате роста цены с 4 до 7 долл., объем спроса на товар Х упал с 1000 до 800 штук. Определите коэффициент эластичности спроса по цене.

Технология решения задачи: Коэффициент эластичности обозначим Еd/р, тогда

Поставив в формулу значения, получим:

Этот коэффициент характеризует малоэластичный товар.

Ответ: коэффициент эластичности равен –0,4; это малоэластичный товар.

Задача 4

Постановка задачи: Цена на товар А выросла со 100 до 200 ден. ед. Спрос на этот товар упал с 3000 до 1000 штук. Спрос на товар В вырос с 500 до 1000. Определите коэффициенты эластичности товара А и В. О каких коэффициентах идет речь?

Технология решения задачи: Так как цена товара А выросла, а спрос на этот товар упал, то можно определить коэффициент ценовой эластичности товара А:

Поставив в формулу значения, получим:

Реакцию спроса товара В на изменение цены товара А показывает коэффициент перекрестной эластичности, который определяется по формуле

Подставим значения и получим:

Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга.

Ответ: коэффициент ценовой эластичности товара А составляет (–1,5), коэффициент перекрестной эластичности +1.

Задача 5

Постановка задачи: Цена на товар А выросла со 10 до 15 ден. ед. Спрос на товар В вырос с 1000 до 2000 штук, на товар С упал с 50 до 40 кг. Определите коэффициенты перекрестной эластичности.

Технология решения задачи:

Сначала рассчитываем коэффициент перекрестной эластичности товара В по формуле

Подставим значения и получим:

Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга.

Затем определяем коэффициент перекрестной эластичности товара С по такой же формуле:

Подставим значения и получим:

Поскольку коэффициент отрицательный, то речь идет о товарах, взаимодополняющих друг друга.

Задача 6

Постановка задачи: Цена на товар А выросла со 1 до 4 ден. ед. Спрос на товар В упал с 3000 до 1000 штук. Спрос на товар С вырос с 500 до 1000, на товар Д не изменился. Определите коэффициенты перекрестной эластичности.

Технология решения задачи:

Сначала рассчитываем коэффициент перекрестной эластичности товара С по формуле

Подставим значения и получим:

Поскольку коэффициент положительный, то речь идет о товарах, взаимозаменяющих друг друга.

Затем определяем коэффициент перекрестной эластичности товара В по такой же формуле:

Подставим значения и получим:

Поскольку коэффициент отрицательный, то речь идет о товарах, взаимодополняющих друг друга.

Поскольку спрос на товар Д не изменился, коэффициент перекрестной эластичности равен 0, т. е. товары являются нейтральными.

Задача 7

Постановка задачи: На рынке товара А объем спроса определяется формулой . Определите эластичность спроса в точке, соответствующей Q = 10.

Технология решения задачи: Для решения задачи необходимо применить формулу расчета коэффициента точечной эластичности:

, где B – коэффициент, показывающий угол наклона кривой спроса. Сначала надо найти цену: , следовательно, Р = 4. Отсюда .

Ответ: коэффициент эластичности равен 0,8.

Задача 8

Постановка задачи: Спрос на товар Х определяется формулой . Определите коэффициент эластичности при цене, равной 30 у. е.

Технология решения задачи: Для решения задачи необходимо применить формулу расчета коэффициента точечной эластичности:

, где B – коэффициент, показывающий угол наклона кривой спроса. Найдем объем спроса при заданной цене:

30 = 60 – 2 Qd, отсюда Qd = 15. Подставив значения в формулу, получим:

Задача 9

Постановка задачи: На рынке товара две группы потребителей, функции спроса которых записываются следующими формулами: , . Определите, какой будет эластичность спроса по цене в точке, соответствующей Qd, равной 12.

Технология решения задачи: Сначала определяется формула рыночного спроса на товар: Q_d1 + Q_d2 = 12 – Р + 12 – 3Р = 24 – 4Р. Находим цену товара при объеме спроса на рынке, равном 12 единиц: 12 = 24 – 4Р; Р = 3. Затем, применяя формулу точечной эластичности, находим коэффициент эластичности:

, где B – коэффициент, показывающий угол наклона кривой спроса.

Задача 10

Постановка задачи: Функция спроса на товар имеет вид Qd = 50 – 2Р. Определите дуговую эластичность спроса по цене при снижении цены с 10 до 9 евро.

Технология решения задачи: Определяем объем спроса при цене 10 евро: , а затем при цене 9 евро:

. После этого рассчитываем коэффициент эластичности:

Задачи на использование коэффициентов эластичности

Задача 11

Постановка задачи: Ценовая эластичность спроса населения на товар составляет (–0,8), а эластичность спроса по доходу 1,3. Если цена на товар снизится на 2 %, а доход увеличится на 5 %, что произойдет со спросом на данный товар?

Технология решения задачи: Объем спроса увеличится под воздействием снижения цены товара и увеличения дохода с учетом коэффициентов эластичности. Это рассчитывается следующим образом:

, где Inc – доход потребителя. Подставив значения, получим:

Ответ: Объем спроса увеличится на 8,1 %.

Задача 12

Постановка задачи: Коэффициент перекрестной эластичности Еx/y = (–2). Цена товара Y равна 100 у. е. Определите спрос на товар Х, если цена товара Y увеличится на 10 %, а первоначальный спрос на товар Х равен 80 т.

Технология решения задачи: Для решения задачи необходимо воспользоваться формулой расчета коэффициента перекрестной эластичности товара Х по формуле

Следовательно, изменение объема спроса товара Х определяется путем перемножения коэффициента перекрестной эластичности на изменение цены товара У: . Следовательно, объем спроса будет равен: Qdх = 80 * 0,95 = 76 т.

Задача 13

Постановка задачи: При цене 10 у. е. объем спроса на товар А равен 1000 штук. Предприниматель решает изменить цену. Он определил, что при росте цены на 10 % эластичность товара становится равной (–1,2), при снижении цены на 10 % коэффициент эластичности равен (–0,8). На какой цене остановится предприниматель?

Технология решения задачи: Для решения задачи надо определить, каким станет спрос при новой цене, а затем рассчитать выручку от продажи товара. При цене 10 у. е. предприниматель получает 10 000 у.е. Если цена снизится на 10 %, она станет равна 9 у. е., спрос на товар вырастет на , т. е. станет 1000 * 1,08 = 1080 штук. Предприниматель получит от продажи этих товаров:

у. е. Выручка сократилась на 10 000 – 9720 = 280 у. е., следовательно, снижать цену нельзя.

Если цена увеличится на 10 %, т. е. станет 11 у. е., спрос на товар упадет на 12 % (1,2 * 10 %), т. е. станет равен . Продавая их по 11 у. е., предприниматель выручит 9680 у. е. Выручка снова сократилась, значит, увеличивать цену на 10 % тоже нельзя. Поэтому предпринимателю следует сохранить старую цену.

Частные коэффициенты эластичности

Пример . 1. Оценка уравнения регрессии. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор получается из выражения:
s = (X T X) -1 X T Y
Матрица X

Можно также посмотреть, как было найдено решение аналогичного примера.
Видеоинструкция
Матрица Y
Матрица X T

Умножаем матрицы, (X T X)

24	4459.4	1907.7	214.2	417.47
4459.4	907391.96	353017.36	40134.04	87383.93
1907.7	353017.36	152366.77	17041.58	33412.82
214.2	40134.04	17041.58	1921.32	3807
417.47	87383.93	33412.82	3807	8907.78

В матрице, (X T X) число 24, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
Умножаем матрицы, (X T Y)

2743.3

557558.59

218286.47

24740.08

54488.32

Находим определитель det(X T X) T = 871494173124.25
Находим обратную матрицу (X T X) -1

67.5762	-0.0883	-0.4341	-3.3069	0.7404
-0.0883	0.0002	0.0006	0.0037	-0.0012
-0.4341	0.0006	0.0036	0.0134	-0.0047
-3.3069	0.0037	0.0134	0.2444	-0.0358
0.7404	-0.0012	-0.0047	-0.0358	0.01

Вектор оценок коэффициентов регрессии равен
s = (X T X) -1 X T Y =

-55.01

0.43

0.86

-1.14

0.95

Уравнение регрессии (оценка уравнения регрессии)
Y = -55.0117 + 0.4315X 1 + 0.8571X 2 -1.1392X 3 + 0.9481X 4
2. Матрица парных коэффициентов корреляции.
Число наблюдений n = 24. Число независимых переменных в модели ровно 4, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 6. Матрица, независимых переменных Х имеет размерность (24 х 6). Матрица Х T Х определяется непосредственным умножением или по следующим предварительно вычисленным суммам.
Матрица составленная из Y и X
Транспонированная матрица.
Матрица A T A.

24	2743.3	4459.4	1907.7	214.2	417.47
2743.3	344649.05	557558.59	218286.47	24740.08	54488.32
4459.4	557558.59	907391.96	353017.36	40134.04	87383.93
1907.7	218286.47	353017.36	152366.77	17041.58	33412.82
214.2	24740.08	40134.04	17041.58	1921.32	3807
417.47	54488.32	87383.93	33412.82	3807	8907.78

Полученная матрица имеет следующее соответствие:

∑n	∑y	∑x1	∑x2	∑x3	∑x4
∑y	∑y 2	∑x1·y	∑x2·y	∑x3·y	∑x4·y
∑x1	∑x1·y	∑x1 2	∑x2·x1	∑x3·x1	∑x4·x1
∑x2	∑x2·y	∑x2·x1	∑x2 2	∑x3·x2	∑x4·x2
∑x3	∑x3·y	∑x3·x1	∑x3·x2	∑x3 2	∑x3·x4
∑x4	∑x4·y	∑x4·x1	∑x4·x2	∑x4·x3	∑x4 2

Найдем парные коэффициенты корреляции.
Для y и x 1
Уравнение имеет вид y = ax + b
Средние значения

Для y и x 2
Уравнение имеет вид y = ax + b
Средние значения

Для y и x 3
Уравнение имеет вид y = ax + b
Средние значения

Для y и x 4
Уравнение имеет вид y = ax + b
Средние значения

Для x 1 и x 2
Уравнение имеет вид y = ax + b
Средние значения

Для x 1 и x 3
Уравнение имеет вид y = ax + b
Средние значения

Для x 1 и x 4
Уравнение имеет вид y = ax + b
Средние значения

Для x 2 и x 3
Уравнение имеет вид y = ax + b
Средние значения

Для x 2 и x 4
Уравнение имеет вид y = ax + b
Средние значения

Для x 3 и x 4
Уравнение имеет вид y = ax + b
Средние значения

Матрица парных коэффициентов корреляции.

—	y	x 1	x 2	x 3	x 4
y	1	0.97	0.05	0.47	0.95
x 1	0.97	1	-0.19	0.38	0.86
x 2	0.05	-0.19	1	0.18	0.21
x 3	0.47	0.38	0.18	1	0.65
x 4	0.95	0.86	0.21	0.65	1

Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых r yxi j y) > r(x k x j ) ; r(x k y) > r(x k x j ).
Если одно из неравенств не соблюдается, то исключается тот параметр x k или x j , связь которого с результативным показателем Y оказывается наименее тесной.
3. Анализ параметров уравнения регрессии.
Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка e = Y — X*s (абсолютная ошибка аппроксимации)

10.93
9.67
9.31
9.91
9.05
7.65
7.11
8.68
12.84
12.97
15.56
22.48
13.97
14.04
15.95
12.88
15.87
15.08
16.81
19.89
22.34
24.13
24.08
21.31

s e 2 = (Y — X*s) T (Y — X*s)
Несмещенная оценка дисперсии равна

Оценка среднеквадратичного отклонения равна

Найдем оценку ковариационной матрицы вектора k = σ*(X T X) -1

1183.8	-1.55	-7.6	-57.93	12.97
-1.55	0	0.01	0.06	-0.02
-7.6	0.01	0.06	0.23	-0.08
-57.93	0.06	0.23	4.28	-0.63
12.97	-0.02	-0.08	-0.63	0.17

Дисперсии параметров модели определяются соотношением S 2 i = K ii , т.е. это элементы, лежащие на главной диагонали
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле

Частные коэффициент эластичности E 1 2 3 4 2 = 0.9 2 = 0.81
т.е. в 81.2384 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T табл (n-m-1;a) = (19;0.05) = 1.729
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

4. Оценка значения результативного признака при заданных значениях факторов.
Y(0.0,0.0,0.0,0.0,) = -55.01 + 0.4315 * 0.0 + 0.8571 * 0.0-1.1392 * 0.0 + 0.9481 * 0.0 = -55.01
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака.
S 2 = X 0 T (X T X) -1 X 0
где
X 0 T = [ 1 0.0 0.0 0.0 0.0]
(X T X) -1

67.5762	-0.0883	-0.4341	-3.3069	0.7404
-0.0883	0.0002	0.0006	0.0037	-0.0012
-0.4341	0.0006	0.0036	0.0134	-0.0047
-3.3069	0.0037	0.0134	0.2444	-0.0358
0.7404	-0.0012	-0.0047	-0.0358	0.01

X 0

1

0

0

0

0

S 2 = 67.58

(Y — t*S Y ; Y + t*S Y )
(-55.01 — 1.729*144.01 ; -55.01 + 1.729*144.01)
(-304;193.98)
Доверительные интервалы с вероятностью 0.95 для среднего значения результативного признака.

(-55.01 — 1.729*145.07 ; -55.01 + 1.729*145.07)
(-305.84;195.82)
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика

Статистическая значимость коэффициента регрессии b 0 не подтверждается

Статистическая значимость коэффициента регрессии b 1 подтверждается

Статистическая значимость коэффициента регрессии b 2 подтверждается

Статистическая значимость коэффициента регрессии b 3 не подтверждается

Статистическая значимость коэффициента регрессии b 4 подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b i — t i S i ; b i + t i S i )
b 0 : (-114.5003;4.477)
b 1 : (0.3419;0.521)
b 2 : (0.4234;1.2908)
b 3 : (-4.7171;2.4386)
b 4 : (0.2255;1.6707)
2) F-статистика. Критерий Фишера

Fkp = 2.74
Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
6. Проверка на наличие гетероскедастичности методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X i , а по оси ординат квадраты отклонения e i 2 .

📺 Видео