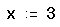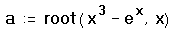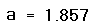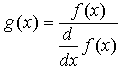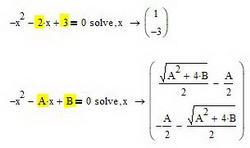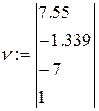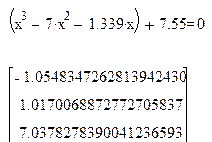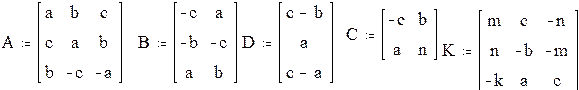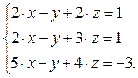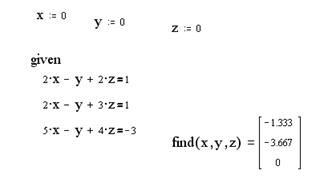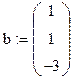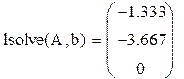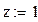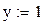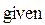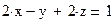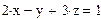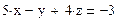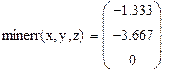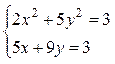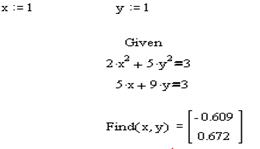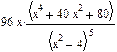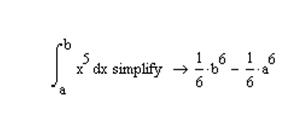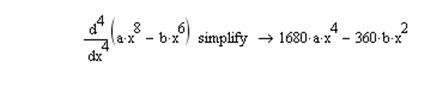Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 — e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
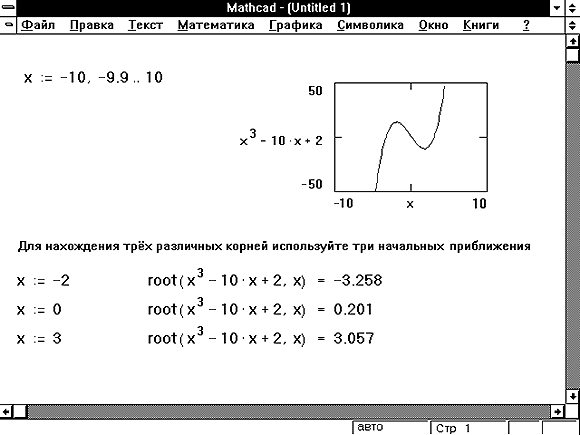
- Для выражения с несколькими корнями, например x 2 — 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) — g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
- Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать

Решение уравнений в MathCad
Для решения уравнений в Mathcad можно воспользоваться двумя способами:
Видео:Mathcad-09. Пример: уравненияСкачать

Использование метода Given — Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
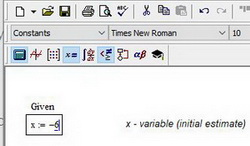
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
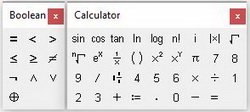
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
После уравнения вводится функция Find(x) (где х — переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах
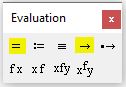
Для получения результата, после Find(x) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 3). Причем, если вы используете символ «→«, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ «=«, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель «Evaluation»
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата
Рис. 5. Результат символьного решения уравнения
Видео:Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа «ровно» из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given — Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Видео:Числовое решение. Функция polyroots в MathCAD 14 (27/34)Скачать

Нахождение корней уравнения в MathCad
Дата добавления: 2015-07-23 ; просмотров: 17986 ; Нарушение авторских прав
Цель работы:нахождение корней уравнения в программе MathCad с использованием встроенных функций root,polyroots, символьного решения.
Указания к выполнению лабораторной работы:
IНахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad .
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора r T .
4. Для интервала нахождения корня и количества элементов вектора r T создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4. Выделить переменную, относительно которой решается уравнение.
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
ІV Найти приближенное решение с использованием функции mіnerr(x1. ).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr( x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
| № варианта | Интервал нахождения корней | Уравнение |
| [-1; 3] | x 3 -2,92x 2 +1,4355x+0,791=0 | |
| [-2; 3] | x 3 -2,56x 2 -1,325x+4,395=0 | |
| [-3,5; 2,5] | x 3 +2,84x 2 -5,606x-14,766=0 | |
| [-2,5; 2,5] | x 3 +1,41x 2 -5,472x-7,38=0 |
| [-1,6; 1,1] | x 3 +0,85x 2 -0,432x+0,044=0 |
| [-1,6; 1,6] | x 3 -0,12x 2 -1,478x+0,192=0 |
| [-1,6; 0,8] | x 3 +0,77x 2 -0,251x-0,017=0 |
| [-1,4; 1] | x 3 +0,88x 2 -0,3999x-0,0376=0 |
| [-1,4; 2,5] | x 3 +0,78x 2 -0,827x-0,1467=0 |
| [-2,6; 1,4] | x 3 +2,28x 2 -1,9347x-3,90757=0 |
| [-2,6; 3,2] | x 3 -0,805x 2 -7x+2,77=0 |
| [-3; 3] | x 3 -0,345x 2 -5,569x+3,15=0 |
| [-2; 3,4] | x 3 -3,335x 2 -1,679x+8,05=0 |
| [-1; 2,8] | x 3 -2,5x 2 +0,0099x+0,517=0 |
| [-1,2; 3] | x 3 -3x 2 +0,569x+1,599=0 |
| [-2,5; 2,5] | x 3 -2,2x 2 +0,82x+0,23=0 |
| [-1,2; 4,6] | x 3 -5x 2 +0,903x+6,77=0 |
| [-1; 7,4] | x 3 -7,5x 2 +0,499x+4,12=0 |
| [-1.6; 9] | x 3 -7,8x 2 +0,899x+8,1=0 |
| [-3,4; 2] | x 3 +2x 2 -4,9x-3,22=0 |
| [-3,4; 1,2] | x 3 +3x 2 -0,939x-1,801=0 |
| [-4,6; 3,0] | x 3 +5,3x 2 +0,6799x-13,17=0 |
| [-2,4; 8,2] | x 3 -6,2x 2 -12,999x+11,1=0 |
| [-3,2; 2,7] | x 3 -0,34x 2 -4,339x-0,09=0 |
| [-1; 3] | x 3 -1,5x 2 +0,129x+0,07=0 |
| [-1; 3] | x 3 -5,5x 2 +2,79x+0,11=0 |
| [-1; 3] | x 3 -5,7x 2 -6,219x-2,03=0 |
| [-1; 3] | x 3 -3,78x 2 -7,459x-4,13=0 |
| [-1; 3] | x 3 -5x 2 -9,9119x+0,01=0 |
| [-1; 3] | x 3 -7x 2 -1,339x-7,55=0 |
Пример
І Для уравнения 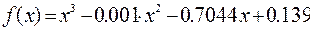
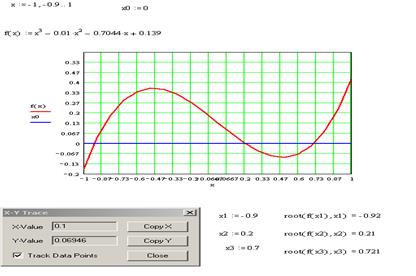
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функции 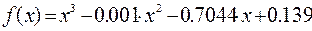
3 Построить графики для этих функций.
4 Определить на графике точки пересечения кривых 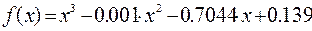
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
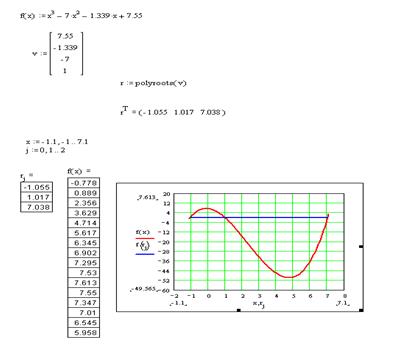
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).
Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения 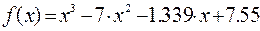
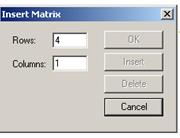
1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.
Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид
2. С помощью встроенной функции r:=polyroots(v) найти корни уравнения и представить их в виде вектора r T , транспонированного по отношению к r, то есть преобразованного из столбца в строку.
3. Создать циклы для переменной х и количества найденных корней:
4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения 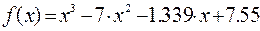
1. Записать левую часть уравнения
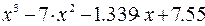
2. Поставить логический знак «=» и в правой части записать 0.
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:
IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr( x1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr( x). Корень будет найдено.
5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.
Контрольные вопросы
1 Какие встроенные функции позволяют находить корни уравнения?
2 Как выполняется символьное нахождение корней уравнений?
Лабораторная работа №3
Действия с матрицами в MathCad
Цель работы:выполнение действий с матрицами в программе MathCad .
Указания к выполнению лабораторной работы:
1. Запустить программу MathCad .
2. Создать матрицы 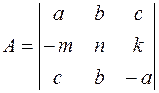
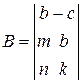
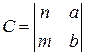
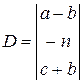
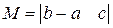
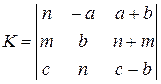
3. Выполнить действия с матрицами в соответствии с вариантом задания.
4. Найти ранг матрицы А.
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А.
6. Найти обратную матрицу К. Найти детерминант матрицы А.
Таблица 2.1 – Варианты заданий к лабораторной работе № 2
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
Продолжение табл. 2.1
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
Пример
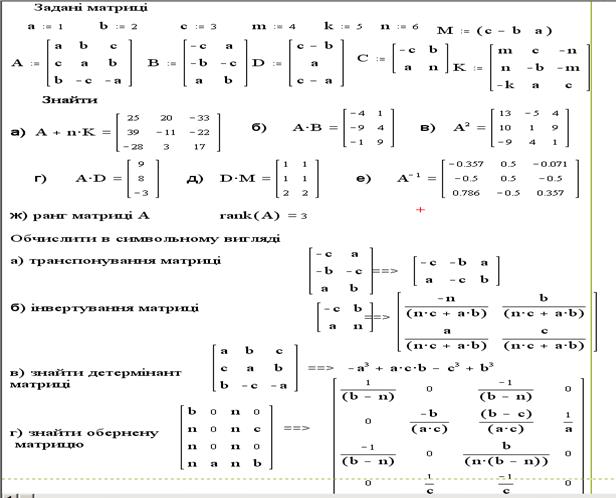
Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:
1. Создать матрицы.
1.1. Выбрать панель управления Matrіx (Матрица).
1.2. Определить число строк и столбцов для каждой матрицы (рис.21).
Рисунок 21 — Диалоговое окно для определения размера матрицы
1.3. Матрицы в примере имеют такие размеры: А — (3´3), В — (3´2), С(2´2), М(1´2), К(3´3).
1.4. Заполнить матрицы соответствующими параметрами (рис. 29).
2 Выполнить следующие действия с матрицами:
1) А+n·K; 2)A·B; 3) A 2 ; 4) A·D; 5)D·M; 6) D-1.
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).
4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.
4.1 Выделить матрицу В.
4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 28).
5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А) .
5.1 Выделить матрицу A.
5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.28).
6 В символьном виде найти обратную матрицу К.
6.1 Выделить матрицу К.
6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.28).
7 В символьном виде найти детерминант (определитель) матрицы А.
7.1 Выделить матрицу A.
7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).
Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде
Рисунок 23 – Результаты вычисления матриц
Контрольные вопросы
1 Як можно создать матрицу и вектор?
2 Какие действия выполняются с матрицами?
3 Как определяются элементы матрицы?
Лабораторная работа №4
Нахождение решений системы линейных уравнений в MathCad
Цель работы:нахождение решений системы линейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
I Найти решение системы линейных уравнений с использованием функции soln.
1 Запустить программу MathCad.
2 Создать матрицу А из коэффициентов при неизвестных.
3 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений soln и записать soln1:=А -1 ×b.
5 Получить решение линейного уравнения у векторному виде
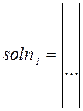
IIНайти решение системы линейных уравнений с использованием так званого «блоку решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частью уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1Создать матрицу А из коэффициентов при неизвестных.
2 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений lsolve и записать lsolve(А,b).
5 Получить результат решения линейного уравнения в векторном виде
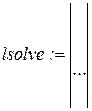
IVНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближение последовательно для значений переменной х1, х2,… хn.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции minerr( x1,x2. ). Значения неизвестных будут найдены.
Таблица 3.1 – Варианты заданий к лабораторной работе № 3
| № варианта | Коэффициенты при неизвестных | Свободные члени | ||
| a11 а21 а31 а41 | а12 а22 а23 а24 | а13 а23 а33 а34 | а14 а24 а34 а44 | в1 в2 в3 в4 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 3,7 | 5,6 | 9,5 | ||
| 3,36 | 31,1 | 1,5 | ||
| 7,93 | 4,2 | 6,3 | 4,4 | |
| 42,7 | 3,7 | 6,2 | ||
| 1,3 | 1,6 | 2,2 | ||
| 4,4 | 6,7 | 2,5 | ||
| 2,8 | 0,73 | 67,8 | ||
| 3,4 | ||||
| 5,3 | 1,6 | 5,5 | 3,3 | |
| 4,1 | 6,4 | 3,9 | ||
| 2,1 | 3,3 | 2,04 | 4,9 | |
| 3,1 | ||||
| 0,2 | ||||
| 8,3 | 5,3 | |||
| 2,6 | 6,1 | 4,1 | ||
| 0,93 | 3,8 | |||
| 34,7 | ||||
| 3,6 | ||||
| 3,4 | 4,2 | |||
| 44,7 | ||||
| 5,1 | 0,2 | |||
| 3,4 | 5,34 | |||
| 2,7 | 6,7 | |||
| 3,3 | ||||
| 2,5 | 1,3 | |||
| 5,2 | 0,78 | |||
| 6,11 | 4,2 | |||
| 6,78 | 3,76 | |||
| 2,3 | ||||
| 3,4 | 2,5 | |||
| 0,2 | ||||
| 1,25 | ||||
| 3,3 | 8,2 | |||
| 1,2 | ||||
| 1,3 | ||||
| 5,9 | ||||
| 6,6 | ||||
| 3,3 | 2,1 | |||
| 4,8 | ||||
| 0,4 | ||||
| 0,2 | ||||
| 1,3 | 1,5 | 2,22 | 3,2 | |
| 3,4 | 5,55 | 1,3 | ||
| 3,3 | 2,2 | 6,77 | ||
| 4,9 | 3,6 | 6,88 | ||
| 0,4 | ||||
| 0,3 | ||||
| 3,3 | 7,6 | 5,5 | ||
| 5,4 | ||||
| 9,2 | ||||
| 3,2 | ||||
| 0,44 | ||||
| 0,67 |
| 3,35 | 5,3 | |||
| 4,22 | 6,7 | 3,5 | ||
| 2,8 | 3,8 | 2,9 | ||
| 2,34 | 3,44 | |||
| 5,23 | ||||
| 13,4 | 6,33 | 5,1 | 2,11 | 3,33 |
| 4,66 | 6,1 | 3,33 | 5,44 | 0,11 |
| 2,22 | 2,55 | 6,33 | 4,44 | |
| 2,98 | 3,78 | 6,11 | 3,33 |
Пример
I Найти решение системы уравнений с использованием функции soln
1 Создать матрицу А
А:= 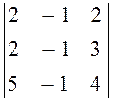
2 Создать вектор b
b:= 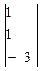
3 Найти решение системы, используя функцию soln
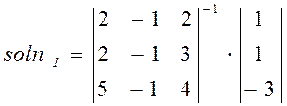
4 Результат решения
II Найти решение вышеприведенной системы уравнений с использованием так званого «блоку решений»
1 Задать начальные значения переменным, которые присутствуют в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1 Создать матрицу А
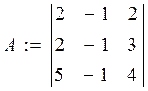
2 Создать вектор b
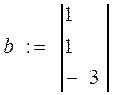
3 Найти решение системы, используя функцию lsolve:
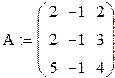
IVНайти решение вышеприведенной системы уравнений с использованием функции minerr (x,у,z).
1 Задать начальные условия для неизвестных, например, x=1,у=1,z=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели.
4 Обратиться к функции minerr (x,у,z). Решение системы уравнений будет найдено.
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы линейных уравнений?
2 В каком виде представляются результаты решения системы линейных уравнений?
Лабораторная работа №5
Нахождение решений системы нелинейных уравнений в MathCad
Цель работы: нахождение решений системы нелинейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
І Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления.
4 Ввести ключевое слово fіnd (найти), которым заканчивается блок решений.
ІІ. Найти приближенное решение с использованием функции mіnerr(x1. ).
1 Задать приближение последовательно для значений переменной х1, х2. хn.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции mіnerr( x1,x2. ). Значение неизвестных будет найдено.
Таблица 4.1 – Варианты задания к лабораторной работе №4
| № варианта | Система уравнений | № варианта | Система уравнений |
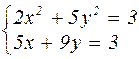 | 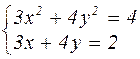 | ||
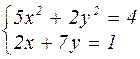 | 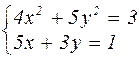 | ||
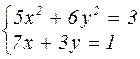 | 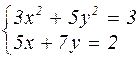 | ||
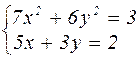 | 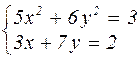 | ||
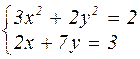 | 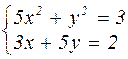 | ||
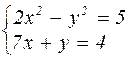 | 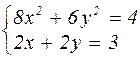 | ||
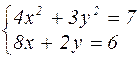 | 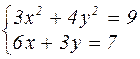 | ||
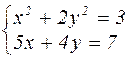 | 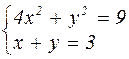 | ||
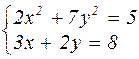 | 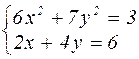 | ||
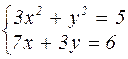 | 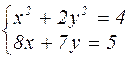 | ||
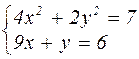 | 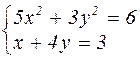 | ||
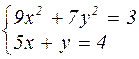 | 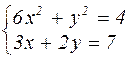 | ||
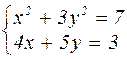 | 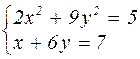 | ||
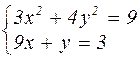 | 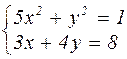 | ||
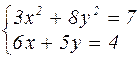 | 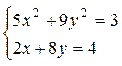 |
Пример
Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели управления
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближения последовательно для значений переменной х=1, y=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и лево частью каждого уравнения.
4 Обратится к функции minerr( x,y.). Значение неизвестных будет найдено.
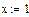 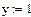 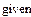 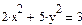 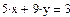 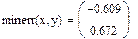 . . |
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы нелинейных уравнений?
2 В каком виде представляются результаты решения системы нелинейных уравнений?
3 Нужно ли задавать начальные приближения при решении системы нелинейных уравнений?
Лабораторная работа № 6
Символьные действия математического анализа в MathCad
Цель работы:определение неопределенных и определенных интегралов и производных в программе MathCad с использованием символьных операций.
Указания к выполнению лабораторной работы:
1 Запустить программу MathCad.
2 Записать на рабочем листе в соответствии с номером варианта формулы для определения неопределенных интегралов, определенных интегралов, производных первого порядка. От производных первого порядка определить производные второго, третьего порядков.
3 Применить последовательно к каждой функции команды меню Symbolic/Simplify, отметив последовательно каждую из функций.
Таблица 5.1 – Варианты задания к лабораторной работе №5
| Номер варианта | Неопределенные интегралы | Определенные интегралы | Производные |
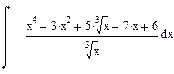 | 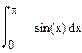 | 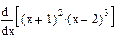 | |
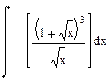 | 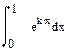 | 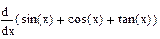 | |
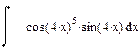 | 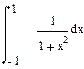 | 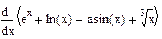 | |
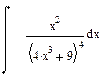 | 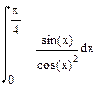 | 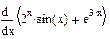 | |
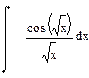 | 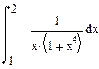 | 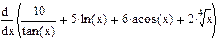 | |
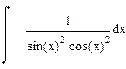 | 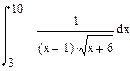 | 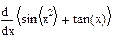 |
Продолжение табл. 5.1
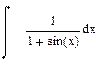 | 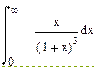 | 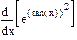 |
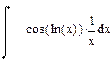 | 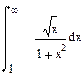 | 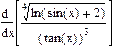 |
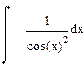 | 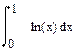 | 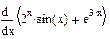 |
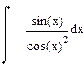 | 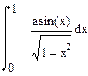 | 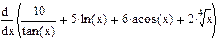 |
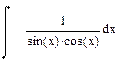 | 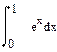 | 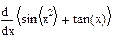 |
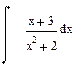 | 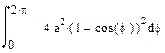 | 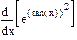 |
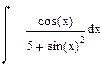 | 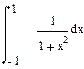 | 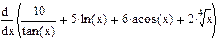 |
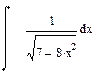 | 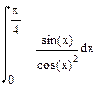 | 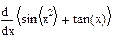 |
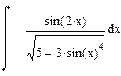 | 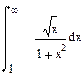 | 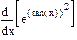 |
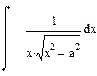 | 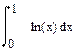 | 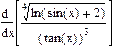 |
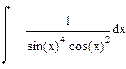 | 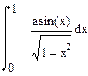 | 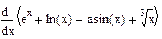 |
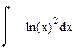 | 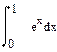 | 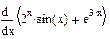 |
Продолжение табл. 5.1
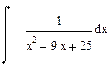 | 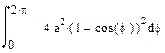 | 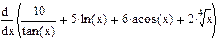 |
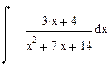 | 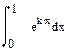 | 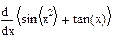 |
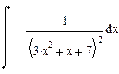 | 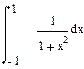 | 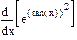 |
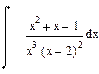 | 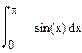 | 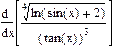 |
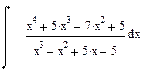 | 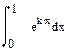 | 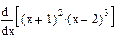 |
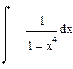 | 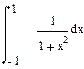 | 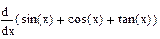 |
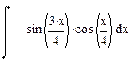 | 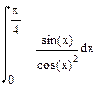 | 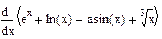 |
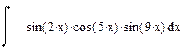 | 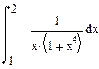 | 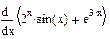 |
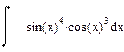 | 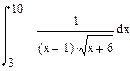 | 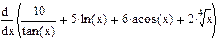 |
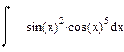 | 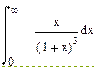 | 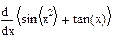 |
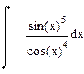 | 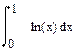 | 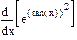 |
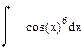 | 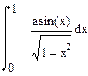 | 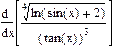 |
Примеры
1 Найти неопределенный интеграл 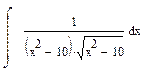
Результат 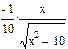
2 Найти определенный интеграл 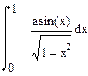
Результат 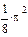
3 Найти производные первого порядка 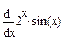
Результат 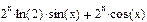
4 Найти производные высокого порядка 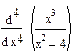
Результат
Контрольные вопросы
1 Как найти в символьном виде определенные и неопределенные интегралы?
2 Можно ли применять символьные операции к интегралам по области, к трехмерным интегралам, к контурным интегралам?
3 Можно ли в символьному виде найти производные высоких порядков?
| | | следующая лекция ==> | |
| Задание 3. | | | Лабораторная работа № 1 |
Не нашли то, что искали? Google вам в помощь!
🎦 Видео
Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

MathCAD Поиск корней полиномаСкачать

Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Математика это не ИсламСкачать

MathCAD. Given - FindСкачать

Дискретные переменные в MathCAD 14 (9/34)Скачать

Ключевое слово solve в MathCAD 14 (26/34)Скачать

MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Определение количества корней уравнения (ДВИ)Скачать

Отбор корней по окружностиСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

MathCAD Решение системы уравненийСкачать

Решение СЛАУ в пакете MathCadСкачать

Вычисление простых выражений в MathCAD 14 (4/34) Часть 1Скачать

Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать