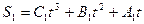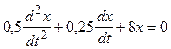- Теоретическая механика: Вращательное движение твердого тела
- § 33. Равномерное вращательное движение
- § 34. Равнопеременное вращательное движение
- § 35. Неравномерное вращательное движение
- Кинематика поступательного и вращательного движений
- Определить угловые скорость и ускорение тела, если угловой путь задан уравнением фи = at2 + b ( рад)?
- Частица движется по окружности радиусом 20 см с начальной угловой скоростью 25 рад / с и угловым ускорением 5 рад / с?
- Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад / с и линейной скоростью 2 м / с?
- Определите центростремительное ускорение материальной точки движущейся по окружности с угловой скоростью 2 рад / с и линейной скоростью 4 м / с?
- Нароооод?
- Тело, которое вращается, увеличило свою угловую скорость с 2 рад / с до 64, 8 рад / с за время, в течение которого произошло 100 полных вращений?
- Угловая скорость вращения составляет 2 рад / с , а радиус окружности 20 см?
- Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад / с и линейной скоростью 2 м / с?
- Угловое ускорение с течением времени изменяется по закону β = 2 + 3t?
- Угловой путь вращающегося тела задан уравнением φ = t ^ 3 + 2t ^ 2 + 4?
- Определите центростремительное ускорение крайних точек диска радиусом 30 см, если он вращается с угловой скоростью 4 рад / с?
- 🔥 Видео
Теоретическая механика:
Вращательное движение твердого тела
Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.
Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.
Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.
Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.
Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими at и an.
Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).
Закон вращательного движения тела выражается уравнением
φ = f (t).
Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).
Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).
Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φоб.
Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.
Так как один полный оборот соответствует 2π рад, то
φ = 2πφоб и φоб = φ/(2π).
Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.
Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.
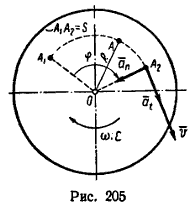
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, at и an, характеризующими движение различных точек этого тела (рис 205).
Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.
Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.
Касательное ускорение точки зависит от углового ускорения и определяется формулой
at = εR.
Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
an = ω 2 R.
При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

§ 33. Равномерное вращательное движение
Если угловая скорость ω=const, то вращательное движение называется равномерным.
Уравнение равномерного вращения имеет вид
φ = φ0 + ωt.
В частном случае, когда начальный угол поворота φ0=0,
φ = ωt.
Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

§ 34. Равнопеременное вращательное движение
Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.
Уравнение равнопеременного вращения
(1) φ = φ0 + ω0t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω0 + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.
В эти формулы входят всего шесть величин: три постоянных для данной задачи φ0, ω0 и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.
Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.
Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ0 + (ω + ω0)t/2.
Исключим из (1) и (2) время t:
(4) φ = φ0 + (ω 2 — ω0 2 )/(2ε).
В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ0=0 и ω0=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).
Видео:Вращательное движение. 10 класс.Скачать

§ 35. Неравномерное вращательное движение
Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.
Видео:Угловая скорость и угловое ускорениеСкачать

Кинематика поступательного и вращательного движений
ЗАДАЧИ
1. Движение точки описывается уравнением: 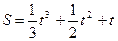
2. В любой момент времени скорость тела равна: 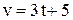
3. Движение точки описывается уравнением: 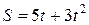
4. Ускорение тела изменяется по закону: a =3t 2 +t (м/с 2 ). Найти скорость тела в конце 2-й секунды от начала движения.
5. Скорость движущегося тела изменяется по закону: v = t 2 + 2t (м/с). Найти путь, пройденный телом за вторую секунду движения.
6. Движение точки описывается уравнением: 
7. Уравнение скорости имеет вид: 
8. Зависимость пройденного телом пути от времени выражается уравнением S=At-Bt 2 +Ct 3 (A=2 м/с, B= 3м/с 2 , C=4м/с 3 ) Запишите выражения для скорости и ускорения. Определите для момента времени t=2с после начала движения:1) пройденный путь; 2) скорость; 3) ускорение.
9. Кинематические уравнения движения двух материальных точек имеют вид
Определите момент времени, для которого ускорения этих точек будут равны. (B1=4 м/с 2 , С1=-3 м/с 3 , В2=- 2 м/с 2 , С2= 1 м/с 2 .)
10. Кинематические уравнения движения двух материальных точек имеют вид
Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента. (B1=4 м/с 2 , С1=-3 м/с 3 , В2=- 2 м/с 2 , С2= 1 м/с 2 .)
11. Зависимость пройденного телом пути от времени задается уравнением
Определить через сколько времени после начала движения ускорение тела будет равно 2 м/с 2 . (С=0.1 м/с 2 ; D=0.03 м/с 3 )
12. Угловая скорость вращающегося тела изменяется по закону w = At + Bt 2 , где A=2 рад/с 2 , В = 3 рад/с 2 . На какой угол повернулось тело за время от t1 = 1 c до t2 = 3 c?
13. Уравнение вращательного движения твердого тела имеет вид: j = A + Bt + Ct 3 , где A = 2 рад, B = 3 рад/с, C = 1 рад/с 2 . Найти: 1) угол j, угловую скорость w и угловое ускорение e в моменты времени t1 = 1 c, t2 = 4 c; 2) среднюю угловую скорость wср за промежуток времени Dt = t2 — t1.
14. Угловой путь вращающегося тела задан уравнением j = 2t 3 + 3t 2 + 8 ( рад). Получить уравнение для углового ускорения.
15. Чему равна угловая скорость тела в конце 1-й секунды вращения, если точка, расположенная на расстоянии 5 см от оси вращения, движется по закону S=t 2 +2t (м)?
16. Чему равна угловая скорость тела в конце 2-ой секунды вращения, если точка, расположенная на расстоянии R = 5 см от оси вращения, движется по закону S = 4 t 2 + 4t ( м ) ?
17. Определить угловые скорость и ускорение тела, если угловой путь задан уравнением j = at 2 + b ( рад).
18. Определить угловое ускорение тела, если линейная скорость точки, движущейся по окружности R = 10 см, задана уравнением v = 2t + 4 (м/с).
19. Какую угловую скорость будет иметь тело к концу второй секунды, если вращение задано уравнением j = 2 t 2 + 4t ( рад).
20. Определить угловое ускорение тела, если линейная скорость точки, движущейся по окружности R = 0,2 см, задана уравнением v = 3t + 4 (м/с).
21. Определить угловую скорость тела к концу 1-ой секунды вращения, если линейная скорость точек тела, движущихся по окружности радиусом 0,1 м задана уравнением v = 2t + 3 (м/с).
22. Угловая скорость тела задана уравнением w = b + et ( с -1 ). Получить уравнение для углового пути.
23. Угловое ускорение вращающегося тела задано уравнением e = 4t + 2. Получить уравнение для угловой скорости.
В следующих задачах выбрать правильный ответ и доказать его.
| № п/п | Задача | Ответ и решение. |
| На каком расстоянии от оси вращения находится точка, если при повороте тела на угол 2 радиана точка прошла путь 0,4 м? | 1) 2 м;2)0,2 м; 3)0,3 м; 4)0,8 м; 5)1 м | |
| Материальная точка вращается по окружности радиусом r = 2м по закону S = 3t 2 (м). Определить ее угловое ускорение | 1) 1 с -2 ; 2)1,5 с -2 ; 3)3 с -2 ;4)6 с -2 ; 5)9 с -2 | |
| Чему равен радиус-вектор точки вращающегося тела, которая при повороте тела на угол 4p радиан прошла путь 1,256 м? | 1)1 м;2)5 м;3)40 см;4)0,2 м;5)10 см | |
| Определить угловой путь вращающегося тела, если точка тела с радиусом-вектором 0,2 м прошла линейный путь 40 см | 1) 2 рад;2)0,2 рад;3)4 рад;5)0,4 рад;6)8 рад | |
| Маховик, бывший неподвижным, начал вращаться с угловым ускорением e = 2 с -2 . Определить угол его поворота за 5 сек. | 1) 0,4 рад;2)25 рад;3)10 рад; 4)50 рад; 5)правильного среди указанных нет | |
| Скорость материальной точки задана уравнением v = 9t 2 + 2t (м/c). Найти закон пути. | 1)3t 2 + 2 t 2 + Const (м);2)3t 3 + t 2 + Const (м); 3)4t 3 +2t 2 + Const (м); 4)6t 3 + t 2 + Const (м); 5)9t 3 +2t 2 + Const (м) | |
| Уравнение вращения тела имеет вид j= t 3 + 4 . Найти угловое ускорение тела в момент времени t = 3 с. | 1) 32 с -2 ; 2) 27 с -2 ; 3) 22 с -2 ; 4) 18 с -2 ; 5) 0 с -2 | |
| Угловой путь вращающегося тела задан уравнением j= t 3 + 2t 2 + 4. Найти уравнение для углового ускорения. | 1) 3t + 2; 2) 6t + 2; 3) 9t + 4; 4) 6t + 4; 5) 6t + 8 | |
| Чему равна угловая скорость тела в конце 1-й секунды вращения, если точка, расположенная на расстоянии 10 см от оси вращения, движется по закону S = 2t 2 + 4t (м). | 1) 50 с -1 ; 2) 100 с -1 ; 3) 80 с -1 ; 4) 12 с -1 ; 5) 8 с -1 | |
| Какую угловую скорость будет иметь тело к концу второй секунды, если вращение задано уравнением j= 2t 2 + 4t ? | 1) 6 с -1 ; 2) 12 с -1 ; 3) 8 с -1 ; 4) 14 с -1 ; 5) 10 с -1 | |
| Угловое ускорение вращающегося тела зависит от времени по закону e = 2t + 4 (c -2 ). Определить угловую скорость тела к концу третьей секунды. | 1) 0,8 c -1 ; 2) 16 c -1 ; 3) 28 c -1 ; 4) 20 c -1 ; 5) 21 c -1 | |
| Угловое ускорение вращающегося тела задано уравнением e = 3t 2 +5 . Найти уравнение для угловой скорости. | 1) t 2 +5t + C; 2) t 3 + 5t + C; 3) 6t + 5 + C; 4) 3(t + t 2 ) + C; 5) 5t 2 + t + C. | |
| Определить угловую скорость тела, если угловое перемещение задано уравнением j= at + b ( рад ) | 1) b (с -1 ); 2) a (с -1 ); 3) 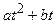 (с -1 ); 4) (с -1 ); 4) 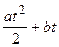 (с -1 ); 5) (с -1 ); 5) 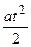 (с -1 ) (с -1 ) | |
| Определить угловое ускорение тела, если линейная скорость точки с радиусом-вектором 0,2 см задана уравнением V = 3t + 4 ( м/с) | 1) 1,5 ×10 3 с -2 ; 2) 10 3 с -2 ; 3) 0,5×10 3 с -2 ; 4) 2×10 3 с -2 ; 5) 100 с -2 | |
| Маховик радиусом r=0,5м вращается с постоянной угловой скоростью w = 4 с -1 . Какова линейная скорость наружных точек маховика? | 1) 0,12 м/с; 2) 1 м/с ; 3) 2 м/с; 4) 4 м/с; 5) 8 м/с | |
| Диск, бывший неподвижным, начал вращаться с угловым ускорением e = 4 рад/с. Определить угол его поворота за 3 секунды. | 1) 0,8 рад; 2) 18 рад; 3) 16 рад; 4) 24 рад; 5) 12 рад | |
График зависимости угла поворота от времени для тела, вращающегося вокруг неподвижной оси, имеет вид, указанный на рисунке. Найти зависимость j = j(t) и указать, какое это вращение  | 1) j = 5 + t , равноускоренное 2) j = 5 + 2,5 t, равноускоренное 3) j = 5 + t, равномерное 4) j = 5 + 2,5 t, равномерное |
II. КОЛЕБАНИЯ
1. Точка колеблется гармонически. Амплитуда колебаний 5 см, циклическая частота 2p ( с -1 ), начальная фаза p/4. Написать уравнение этого колебания.
2. Уравнение гармонических колебаний имеет вид X = 10 sinp(t + 0,5) ( см ). Чему равна фаза этих колебаний через 1,5 с после начала движения?
3. Уравнение гармонических колебаний тела имеет вид X = 2 sin2p(t + 0,1) (м). Чему равен период этого колебания?
4. Уравнение гармонических колебаний имеет вид X = 5 sin(pt/3 + p/4) (см). Определить амплитуду, период, частоту и начальную фазу этого колебания.
5. Чему равна частота гармонических колебаний, график которых изображен на рисунке
6. Чему равна циклическая частота гармонического колебания график зависимости смещения от времени для которого изображен на рисунке.
7. Уравнение гармонического колебания тела имеет вид X = 8 sinp(t + 0,2) (см). Чему равна начальная фаза этого колебания? Результат записать в градусах. Как изменится начальная фаза этого колебания, если смещение будет измеряться в метрах?
8. Построить график колебания и на графике указать амплитуду и период колебания. Уравнение колебания имеет вид 
9. Гармоническое колебание задано уравнением X=5 cos ( 2p+p/4) (см). Получить уравнение для расчета скорости. Чему равна амплитуда скорости?
10. Гармоническое колебание задано уравнением X=5 cos ( p+p/6) (см). Определить амплитуду скорости. Для каких значений X скорость максимальна?
11. Скорость гармонического колебательного движения задана уравнением V=0,1sin(pt + p/6) (м/с). Определить амплитуду этого колебательного движения.
12. Скорость гармонического колебательного движения задана уравнением V=3cos(2pt + p/4) ( м/с). Чему равны: а) период колебаний; б) амплитуда ускорения; в) начальная фаза. При каком значении скорости ускорение принимает максимальное значение?
13. Через какую долю периода скорость точки равна половине ее максимальной скорости, если начальная фаза колебаний равна нулю? Задачу решить математически и проиллюстрировать графически.
14. Уравнение для смещения гармонического колебательно движения задано в виде X=5 cos ( 2pt+p/2) ( мм). Найти выражение для ускорения. Результат представить в системе «СИ».
15. Скорость гармонического колебания задана уравнением V=3cos(2pt+p/4)(см/с). Определить амплитуды смещения и ускорения.
16. Уравнение для смещения при гармоническом колебании задано в виде X=2cos(pt+p/4) ( м ). Найти закон изменения ускорения и построить график ускорения для этого движения.
17. Скорость гармонического колебательного движения задана уравнением V=-sin(2pt+p/4)(м/с). Найти закон изменения ускорения и построить его график.
18. Скорость гармонически колеблющегося тела задана уравнением V=4sin(pt+p/6)(см/с). Найти скорость и ускорение колеблющегося тела в момент времени t=2c от начала движения.
19. Точка совершает гармонические колебания по закону синуса с амплитудой 10 см и периодом 0,2 с. Найти максимальное значение ускорения. Как изменится результат, если колебания будут происходить по закону косинуса?
20. Определить максимальные потенциальную и кинетическую энергии тела массой 2г, колеблющегося по закону X=10sin(2pt+p/3) (м)
21. Тело массой 10 г колеблется со скоростью V = -2sin(2pt+p/2)(м/с). Определить кинетическую энергию к концу 4-ой секунды.
22. Тело массой 100 г колеблется по закону X = cos (3pt +p/4) (см). Определить потенциальную энергию тела в конце 2-ой секунды движения.
23. Тело массой 2 кг совершает гармонические колебания по закону X=5cos(2pt+p/2) (мм). Определить полную энергию тела.
24. Тело массой 1 г колеблется по закону X=2cos(2pt+p/3) (см). Определить потенциальную и кинетическую энергии тела в конце 1-ой секунды движения.
25. Уравнение колебаний материальной точки массой m=16г имеет вид X=2sin(pt/8+p/4) (см), где X выражается в сантиметрах. Определить кинетическую, потенциальную и полную энергию точки через 2 секунды после начала колебаний.
26. Тело массой 5 кг совершает гармонические колебания с амплитудой A = 4см. Найдите период колебаний, если максимальная кинетическая энергия колеблющегося тела равна 0,98 Дж.
27. Полная энергия колеблющегося тела равна 4,5×10 -5 Дж. Максимальная сила, действующая на тело равна 1,5×10 -3 Н. Найти амплитуду колебания.
28. Материальная точка массой 0,05 кг колеблется по закону X=0,1sin(pt/5+p/3)(м). Найти максимальную силу, действующую на точку.
29. Фаза колебаний равна p/3. Величина какого вида энергии: кинетической или потенциальной — больше при этом значении фазы. Во сколько раз?
30. Максимальная потенциальная энергия колеблющегося по гармоническому закону тела массой 1 кг равна 8p 2 Дж. Чему равна амплитуда смещения, если w=4p (с -1 )?
31. Написать уравнение затухающих колебаний, если начальная амплитуда колебания 2 см, коэффициент затухания 0,1 с -1 , период колебания 4 с, начальная фаза равна p/4.
32. Задано уравнение колебаний 
33. Амплитуда затухающего колебания в момент времени t равна 2,7 см, а в момент времени t+T равна 1 см. Определить логарифмический декремент затухания.
34. Рассчитать амплитуду затухающего колебания для момента времени t=5с от начала колебаний, если начальная амплитуда равна 5,7 см, коэффициент затухания — 0,2 с -1 .
35. Чему равен период затухающих колебаний, если коэффициент затухания 0,1с -1 , а логарифмический декремент затухания 0,2?
36. Задано уравнение колебаний 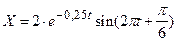
37. Задано уравнение колебаний 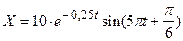
38. Логарифмический декремент затухания математического маятника равен 0,2. Найти, во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника.
39. Частота колебаний равна 100 Гц, коэффициент затухания равен 0,25 с -1 . Определить логарифмический декремент затухания.
40. Дифференциальное уравнение затухающих колебаний имеет вид
Определить коэффициент затухания и циклическую частоту этих колебаний.
III.ВОЛНЫ, ЗВУК, УЛЬТРАЗВУК
1. Написать уравнение плоской незатухающей волны, если амплитуда колебаний 5 см, период 4 с, длина волны 300 м.
2. Уравнение гармонического колебания имеет вид X = 5cos2pt (см). Написать уравнение волны, если скорость распространения колебания 340 м/с. Чему равна длина волны?
3. Источник совершает колебания по закону S=5sin3140t (м). Определить смещение от положения равновесия точки, находящейся на расстоянии 340 м от источника, через Dt = 1 c после начала колебаний. Скорость распространения волны u=340 м/с.
4. Камертон совершает 130 колебаний в секунду. Какова длина волны звука в воздухе, если скорость звука 325 м/с?
5. Найти длину волны колебания, период которого равен 10 -14 сек. Скорость распространения колебаний 3×10 8 м/сек.
6. Найти длину волны основного тона «ля» с частотой 435 Гц. Скорость звука принять равной 340 м/с.
7. Какова частота колебаний, если наименьшее расстояние между двумя точками, колеблющимися в одинаковых фазах, равно 3 м? Скорость распространения колебаний 330 м/с
8. Найти разность фаз колебаний двух точек, лежащих на луче и отстоящих на расстояние 2 м друг от друга, если длина волны равна 1 метру.
9. Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние 

10. Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника колебаний в момент 
11. Найти разность фаз колебаний двух точек, лежащих на луче и отстоящих на расстояние Dx=1,75 м друг от друга, если длина волны l=1м.
12. Какую разность фаз будут иметь колебания двух точек. Находящихся на расстоянии 5 м и 11 м от источника колебаний? Период колебаний 0,02 с, скорость распространения колебаний 300 м/с.
13. Уравнение незатухающих колебаний дано в виде 
14. Уравнение незатухающих колебаний дано в виде 
15. Уравнение незатухающих колебаний дано в виде 
Записать уравнение колебаний для точек волны в момент времени t=4 сек. после начала колебаний.
16. Найти длину волны, если скорость распространения колебаний 300 м/с, а уравнение незатухающих колебаний имеет вид X=2sinpt/3 (см)
17. Разность хода Dx звуковых волн, приходящих в левое и правое ухо человека, составляет 1 см. Определить разность фаз этих волн для тона с частотой n=1000 Гц. Скорость звука 340 м/с.
18. Звуковые колебания, имеющие частоту 

19. Ухо человека может воспринимать звуки частотой приблизительно от 20 до 20000 Гц. Между какими длинами волн лежит интервал слышимости звуковых колебаний? Скорость звука в воздухе считать равной 340 м/с.
20. Определить разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии Dx=20 см друг от друга. Скорость пульсовой волны считать равной U=10 м/с, а колебания сердца- гармоническими с частотой n=1,2 Гц.
21. Интенсивность плоской волны в воздухе равна 10 -8 Вт/м 2 . Найти амплитуду колебаний частиц воздуха, если плотность воздуха r=1,3 кг/м 3 , циклическая частота колебаний 1000 Гц. Скорость распространения колебаний в воздухе 330 м/с
22. Рассчитать волновое (акустическое) сопротивление биологической ткани, если плотность ткани 860 кг/м 3 , а скорость распространения ультразвука в ней 1500 м/с.
23. Интенсивность плоской волны в воздухе равна I=10 -10 вт/м 2 . Найти объемную плотность энергии этой волны. Скорость звука в воздухе 330 м/с.
24. Известно, что ультразвук — это упругие волны в интервале частот от n1=2×10 4 Гц до n1=10 9 Гц. Каким длинам волн соответствует этот интервал в воздухе? В воде? Скорость звука в воздухе и воде равны соответственно V1=340 м/с и V1=1400 м/с.
25. Акустическое сопротивление мышечной ткани человека равно 1,63×10 6 Па×с/м. Определить скорость распространения ультразвука в этой ткани, если ее плотность 1060 кг/м 3 .
26. Одинаковой ли высоты будет казаться звук в случаях: а) источник звука движется навстречу неподвижному наблюдателю со скоростью V1=40м/с? б) наблюдатель движется навстречу неподвижному источнику с той же скоростью? Частота источника звука n=600Гц.
27. Определить скорость движения автомобиля, если наблюдатель, стоящий на шоссе, слышит звуковой сигнал приближающегося автомобиля с частотой n1=3 кГц. Частота колебаний источника звука n=2,8 кГц. Скорость звука принять равной 300 м/с.
28. Две машины движутся навстречу друг другу со скоростями VИ=20 м/с и VН=10 м/с. Первая машина дает сигнал с частотой n1=800Гц. Какой частоты сигнал услышит водитель второй машины а) до встречи машин; б) после встречи машин. Скорость звука в воздухе — 331 м/с.
29. Два поезда идут навстречу друг другу со скоростями 72 км/ч и 54 км/ч. Первый поезд дает свисток с частотой 600 Гц. Найти частоту колебаний звука, который слышит пассажир второго поезда перед встречей поездов. Скорость звука принять равной 340 м/сек.
30. Два поезда идут навстречу друг другу со скоростями 72 км/ч и 54 км/ч. Первый поезд дает свисток с частотой 600 Гц. Найти частоту колебаний звука, который слышит пассажир второго поезда после встречи поездов. Скорость звука принять равной 340 м/сек.
Видео:Решение графических задач на равномерное движениеСкачать

Определить угловые скорость и ускорение тела, если угловой путь задан уравнением фи = at2 + b ( рад)?
Физика | 10 — 11 классы
Определить угловые скорость и ускорение тела, если угловой путь задан уравнением фи = at2 + b ( рад).
Угловой путь задан уравнениемфи = at2 + b( рад).
Полная формулаφ = φ0 + ω0 * t + ε * t ^ 2 / 2
начальная угловая координатаφ0 = b
начальная угловая скоростьω0 = 0
угловое ускорениеε = 2a
уравнение угловой скорости ω = ω0 + ε * t.
Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Частица движется по окружности радиусом 20 см с начальной угловой скоростью 25 рад / с и угловым ускорением 5 рад / с?
Частица движется по окружности радиусом 20 см с начальной угловой скоростью 25 рад / с и угловым ускорением 5 рад / с.
Сему равно тангенсеальное ускорение в момент времени 10 с?
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад / с и линейной скоростью 2 м / с?
Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад / с и линейной скоростью 2 м / с.
Видео:УГЛОВАЯ СКОРОСТЬ кинематика угловое ускорение 10 классСкачать

Определите центростремительное ускорение материальной точки движущейся по окружности с угловой скоростью 2 рад / с и линейной скоростью 4 м / с?
Определите центростремительное ускорение материальной точки движущейся по окружности с угловой скоростью 2 рад / с и линейной скоростью 4 м / с.
Видео:Связь между линейной и угловой скоростьюСкачать

Нароооод?
Срочно((угловая скорост тела 62, 8 рад / c определите период его обращения.
Видео:2.4. Угловая скорость и угловое ускорение твердого тела, вращающегося вокруг неподвижной оси, как векторы.Скачать
Тело, которое вращается, увеличило свою угловую скорость с 2 рад / с до 64, 8 рад / с за время, в течение которого произошло 100 полных вращений?
Тело, которое вращается, увеличило свою угловую скорость с 2 рад / с до 64, 8 рад / с за время, в течение которого произошло 100 полных вращений.
Определите ускорение тела.
Видео:Угловая скорость и радианная мера углаСкачать

Угловая скорость вращения составляет 2 рад / с , а радиус окружности 20 см?
Угловая скорость вращения составляет 2 рад / с , а радиус окружности 20 см.
Определите центростремительное ускорение.
Видео:Скорость движения тела задана уравнениемСкачать

Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад / с и линейной скоростью 2 м / с?
Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад / с и линейной скоростью 2 м / с.
Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Угловое ускорение с течением времени изменяется по закону β = 2 + 3t?
Угловое ускорение с течением времени изменяется по закону β = 2 + 3t.
Начальная угловая скорость = 3 с ^ — 1, начальное угловое положение = 2 рад.
Найти выражение, определяющее угловую скорость и угол поворота как функцию времени.
Видео:Плоско-параллельное движение. Определение скоростей. ТермехСкачать

Угловой путь вращающегося тела задан уравнением φ = t ^ 3 + 2t ^ 2 + 4?
Угловой путь вращающегося тела задан уравнением φ = t ^ 3 + 2t ^ 2 + 4.
Найти для углового ускорения.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Определите центростремительное ускорение крайних точек диска радиусом 30 см, если он вращается с угловой скоростью 4 рад / с?
Определите центростремительное ускорение крайних точек диска радиусом 30 см, если он вращается с угловой скоростью 4 рад / с.
Вы зашли на страницу вопроса Определить угловые скорость и ускорение тела, если угловой путь задан уравнением фи = at2 + b ( рад)?, который относится к категории Физика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.
Поместить в вакуумный пакет, а в итоговом результате отнять его обьем.
1. Сила тока равна отношению ЭДС источника к сумме внешнего и внутреннего сопротивлений. 2. э д. С. равна сумме падения напряжений во внешней и внутренней цепи.
Дано : a = 0. 6м / с ^ 2 S = 30м Найти : t Решение : S = at ^ 2 / a t = корень 2s / a t = корень 60 / 0. 6 = корень 100 = 10 с Ответ : 10с.
Дано vo1 = 4 м / с (начальные скорости) vo2 = — 2 м / с t = 3 c vk1 = vk2 = 0 (точка пересечения графиков) = = = Ускорения a1 = (vk1 — vo1) / t = (0 — 4) / 3≈ — 1. 33 м / с² a2 = (vk2 — vo2) / t = (0 — ( — 2)) / 3≈0. 67 м / с² Уравнения скоростей v..
A = v ^ 2 / r = ω ^ 2 * r так как радиус не ищменяется, то v и ω увеличивается в корень из 1. 94 = 1. 393.
I1 = Uv / R1 = 15 / 10 = 1. 5 A I2 = Uv / R2 = 30 / 10 = 3 A Io = I1 + I2 = 1. 5 + 3 = 4. 5 A (общий ток в цепи) I3 = I4 = Io / 2 = 4. 5 / 2 = 2. 25 A (R3 = R4) R34 = R3 * R4 / (R3 + R4) = 6 / 2 = 3 Ом U34 = I3 * R34 = 2. 25 * 3 = 6. 75 B Uo =..
150 — 50 = 100 100 : 3 = 33, 3обем який вона ковтала що разу.
S = VT S = 18×4 = 72km a = Vo — V / t a = 0 — 18 / 4 = 4. 5м / с2.
Дано : Rпосл = 50 Ом Rпар = 12 Ом R₁ — ? R₂ — ? При последовательном соединении R₁ + R₂ = 50 При параллельном соединении 1 / R₁ + 1 / R₂ = 1 / 12 или (R₁ * R₂) / (R₁ + R₂) = 12 Нужно решить систему двух уравнений. Здесь больше математики, чем физи..
2м / с = 7, 2км / ч 5м / с = 18км / ч 8м / с = 28, 8км / ч 50м / с = 180км / ч 100м / с = 360км / ч.
🔥 Видео
Урок 50. Задачи на вращение с пост. угловым ускорениемСкачать

Определение скорости и ускорения при поступательном и вращательном движении.Скачать

Линейная и угловая скорости при равномерном движении по окружностиСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Кинематика за 8 минСкачать