Видео:Определение реакций опор простой рамыСкачать

Как определить реакции опор твердого тела

Чтобы определить реакции опор твердого тела нужно выполнить следующие шаги.

• Вместо связей в опорах приложить силы реакций.
• Если есть распределенная нагрузка, то заменить ее равнодействующей силой. Ее величина равна площади эпюры нагрузки. Точка приложения находится в центре тяжести эпюры. Так для равномерно распределенной на отрезке нагрузки, ее равнодействующая приложена к середине этого отрезка.
• Выбрать систему координат. Ее начало желательно выбрать в точке крепления одной из опор.
• Составить уравнения равновесия.
  Векторная сумма всех действующих на тело сил (включая реакции опор) равна нулю:
  (1) .
  Векторная сумма моментов этих сил относительно начала системы координат O равна нулю:
  (2) .
• Составить проекции уравнений равновесия (1) и (2) на оси системы координат.
  Суммы проекций сил на оси координат равны нулю:
  (1.x) ;
  (1.y) ;
  (1.z) .
  Суммы моментов сил относительно координатных осей равны нулю:
  (2.x) ;
  (2.y) ;
  (2.z) .
• Для трехмерной задачи мы получим систему из шести уравнений, решая которую, определяем шесть неизвестных проекций реакций опор.
• Для плоской задачи, в которой все действующие силы направлены вдоль осей x и y, получаем три уравнения равновесия: (1.x), (1.y) и (2.z). Из них определяем три неизвестные проекции реакций опор.
• Для упрощения расчетов, иногда бывает полезно спроектировать уравнения равновесия (1) и (2) на другие оси, и составить дополнительные уравнения для моментов относительно других точек. См. Три формы уравнений равновесия твердого тела
• Если полученная система не имеет решения, то при такой схеме закрепления тела равновесие не возможно.
• Если число неизвестных превышает число линейно независимых уравнений, то задача имеет бесконечно много решений, она статически неопределима. Такую задачу можно решить только методами сопротивления материалов. Пример: плоское тело с четырьмя опорами.

Далее мы рассмотрим вопросы, связанные с определением реакций опор твердого тела более подробно и разберем пример решения задачи.

Видео:Определение реакций опор простой рамыСкачать

Методы определения реакций опор твердого тела

Рассмотрим некоторое твердое тело, на которое действуют заданные внешние силы. Пусть оно определенным образом закреплено в некоторых точках – опорах, и находится в состоянии равновесия. Эти точки закрепления также называются связями. Это могут быть шарниры, заделки, поверхности и т. п.

Отбросим опоры, и приложим вместо них силы. Они называются силами реакций опор. Их направления определяются устройствами соответствующих опор. В некоторых опорах реакции возникают в виде пары сил, которые задаются значением момента пары. Нам нужно найти такие значения сил реакций, чтобы при их действии на тело, оно покоилось, как это происходит в закрепленном состоянии.

Воспользуемся двумя законами, которые выполняются, если тело находится в покое.
1) Векторная сумма всех действующих на тело внешних сил равна нулю:
(M.1) .
2) Векторная сумма моментов всех внешних сил относительно любой точки O равна нулю:
(M.2) .
Эти законы называются уравнениями равновесия. В них также включены силы (пары сил) реакций опор.

Самый простой способ составления уравнений равновесия

Разберем самый простой способ составления уравнений равновесия. С его помощью можно гарантированно получить значения сил реакций опор или определить, что схема закрепления тела в опорах является статически неопределимой.

Выберем прямоугольную систему координат с началом в любой точке. Часто за начало системы координат удобно выбрать точку крепления одной из опор, но это не обязательно. Итак, пусть мы выбрали систему координат Oxyz с началом в точке O .

Спроектируем (M.1) на оси этой системы. В результате мы получим три уравнения, связывающие проекции сил на оси xyz :
(M.1.x) ;
(M.1.y) ;
(M.1.z) .
Здесь – n сил, действующих на тело. В их состав также включены и силы реакций опор.

Составим уравнения равновесия (M.2) для моментов, относительно осей Ox , Oy , Oz системы координат:
(M.2.x) ;
(M.2.y) ;
(M.2.z) .
Заметим, что эти уравнения являются проекциями векторного уравнения (M.2) на оси Ox , Oy и Oz .

Уравнения (M.1.x), (M.1.y), (M.1.z) и (M.2.x), (M.2.y), (M.2.z) представляют собой полную систему уравнений равновесия твердого тела. Если мы попытаемся добавить сюда еще одно уравнение, то оно будет являться линейной комбинацией уже существующих уравнений, и никак не повлияет на численные значения определяемых реакций опор. Например, мы можем выбрать еще одну ось, и спроектировать на нее уравнение (M.1) для сил. Или мы можем составить уравнение для моментов (M.2) относительно другой точки, отличной от начала координат. В результате получим дополнительные уравнения, но число линейно независимых уравнений от этого не изменится.

Таким образом, для одного тела, методами статики, мы можем составить максимум шесть независимых уравнений равновесия. В некоторых случаях их число может быть еще меньше.

Так, в случае плоской системы сил, у нас будет всего три независимых уравнения. Чтобы в этом убедиться, выберем систему координат, у которой оси Ox и Oy лежат в плоскости действия сил. Ось Oz перпендикулярна. Тогда проекции всех сил на ось Oz равны нулю. Поэтому уравнение (M.1.z) выполняется автоматически, и его можно вычеркнуть. В уравнениях (M.2.x) и (M.2.y) все силы или пересекают оси Ox и Oy, или параллельны им. Поэтому их моменты относительно этих осей равны нулю. Тогда и уравнения (M.2.x) и (M.2.y) выполняется автоматически. Их также можно вычеркнуть. Остаются три уравнения равновесия (M.1.x), (M.1.y) и (M.2.z).

Неизвестными в уравнениях равновесия являются проекции сил реакций опор на оси координат, или проекции пар сил. При решении этих уравнений могут возникнуть следующие случаи.

1. Число неизвестных совпадает с числом линейно независимых уравнений. Тогда задача статически определима, и мы можем получить значения неизвестных реакций, решив линейную систему уравнений.
2. Число неизвестных меньше числа линейно независимых уравнений и система не имеет решений – при такой схеме закрепления тела равновесие не возможно.
3. Число неизвестных превышает число независимых уравнений – система имеет бесконечное множество решений. Выбрать единственное решение, используя только методы статики, нельзя. Задача является статически неопределимой. Такие задачи решаются методами сопротивления материалов. Например, если балка имеет четыре опоры, то у нас минимум четыре неизвестные величины и три уравнения равновесия (для плоской системы сил). В этом случае, для определения реакций, необходимо учитывать возникающие в балке деформации и напряжения.

Эффективные способы составления уравнений равновесия

Уравнений (M.1) и (M.2) достаточно для определения опорных реакций, но иногда бывает удобным дополнить их другими уравнениями, из которых можно определить реакции более легким способом.

Один из способов заключается в соответствующем выборе начала системы координат. Так, если за ее начало взять точку крепления одной из опор тела, то сила реакции в этой опоре будет пересекать начало координат, и поэтому ее момент будет равен нулю (это не относится к паре сил). Тогда компоненты этих сил реакций не будут входить в уравнения для моментов (M.2.x), (M.2.y), (M.2.z).

Спроектировав уравнение равновесия для сил на ось AD, находим реакцию R_B

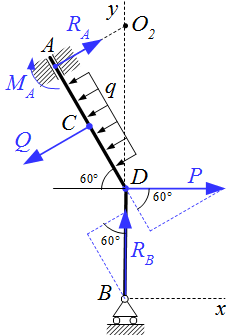
Уравнения (М.1.x) – (М.1.z) представляют собой проекции векторного уравнения (М.1) на оси координат. Но это уравнение можно спроектировать на любую ось. Тогда в него не войдут силы, перпендикулярные выбранной оси. На рисунке слева изображено тело ADB. Реакция в скользящей заделке A состоит из силы R_A и пары сил с моментом M_A; в опоре на катках B – из силы R_B. Для определения только одной реакции R_B, мы можем спроектировать уравнение для сил на ось AD (см. рисунок). Поскольку реакция перпендикулярна этой оси, то ее проекция на AD равна нулю. Равномерно распределенная нагрузка q, и ее равнодействующая Q также перпендикулярна AD. В результате получим уравнение, содержащее только одну реакцию R_B:
;
;
.
Отсюда сразу определяем R_B:
.

Поскольку в равновесии сумма моментов сил равна нулю относительно любой точки, то можно выбрать дополнительную точку, и относительно нее составить уравнение для моментов:
.
Число линейно независимых уравнений при этом не изменится, но мы можем дополнить систему более простым уравнением. См. Три формы уравнений равновесия твердого тела.

Вернемся к нашему примеру ⇑. Пусть нам нужно определить только момент . Тогда можно выбрать точку O₂ на пересечении линий действия сил и . Поскольку эти силы пересекают O₂, то их моменты относительно этой точки равны нулю. Составим уравнение для моментов:
.
Спроектируем его на ось z, перпендикулярную плоскости рисунка:
;
;
.
Отсюда находим :
.

Для трехмерного распределения сил, уравнения (M.2.x), (M.2.y) и (M.2.z) являются проекциями векторного уравнения для моментов (M.2) на оси координат. Но это уравнение можно спроектировать на любую ось, не обязательно параллельной одной из осей системы координат, как мы делали для сил.

Далее приводится подробно разобранный пример решения задачи, в котором требуемая реакция определяется из одного уравнения за счет соответствующего выбора оси, относительно которой вычисляются суммы моментов сил.
Определение реакций опор твердого тела — решение задачи

Автор: Олег Одинцов . Опубликовано: 30-10-2017 Изменено: 06-01-2022

Видео:Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ

Видео:Определение реакций опор в балке. Сопромат.Скачать

З.1 Способы решения задач

Инженерные конструкции часто представляют собой системы тел, соединенных друг с другом какими-нибудь связями. Связи, соединяющие части данной конструкции, будем называть внутренними в отличие от внешних связей, скрепляющих конструкцию с другими телами, в нее не входящими. Соответственно силы взаимодействия между телами системы будем называть внутренними, а силы, действующие на рассматриваемую систему тел со стороны других тел, — внешними. Целью статического расчета системы тел, как правило, является определение реакций внешних и внутренних связей.

Существуют два способа решения задач на равновесие системы тел, методика которых такова:

1) конструкцию расчленяют на отдельные тела и составляют условия равновесия каждого тела в отдельности;

2) рассматривают равновесие всей конструкции целиком и равновесие какой-нибудь одной (если в системе всего две части) или нескольких частей (часть конструкции может быть одним телом либо состоять из нескольких тел).

При расчленении системы тел следует иметь в виду, что, согласно закону взаимодействия тел, силы взаимодействия между телами, например NnN’, должны изображаться векторами, приложенными к соответствующим телам и направленными по одной прямой в противоположные стороны, т._е. на чертеже должно отображаться векторное равенство N’ = -N, а при решении задачи учитываем равенство их алгебраических значений, т. е. N’ = N (например, если расчетом определили, что N = — 8 Н, то N’ = —8 Н).

Например, если тела соединены в точке С цилиндрическим шарниром, ось которого параллельна оси z, то реакцию внутренней связи изображаем двумя составляющими^ к одной части конструкции приложены силы X_C,Y_C, а к другой Х’_с, Y?. При этом Х’_с =-Х_с, Y? =-Y_c (что отображается на чертеже), а в числовых расчетах учитываем равенства Х’_с =Х_С, Y? = Y_c.

Таким образом, система уравнений для решения задачи состоит из зависимостей для двух видов механических явлений: уравнений равновесия тел конструкции и уравнений закона взаимодействия между ее телами.

Задача 3.1. Конструкция состоит из балки АВ и угольника CDE (рис. 3.1). Балка АВ закреплена в точке А шарнирно, в точке С опирается на угольник CDE, который в точке Е имеет жесткую заделку. К конструкции приложена сила F и пара сил с моментом М. Определить реакции связей в точках А, Е и силу взаимодействия тел в точке С, если Е= 30 кН, М = — 40 кН • м, / = 0,5 м, а — 0,8 м, b — 0,4 м, а = 60°, р — 30°.

Решение. Рассмотрим решение задачи двумя способами.

1. Расчленяем систему на балку АВ и угольник CDE и изображаем действующие на каждое тело активные силы и реакции связей (рис. 3.2, а, б), проводим координатные осш_ Отметим, что силы взаимодействия между частями конструкции N_c и N’_c направлены в противоположные стороны, так как N’_c—N_c (см. рис. 3.2, б).

Сначала рассмотрим равновесие балки АВ (см. рис. 3.2, а) и составим для действующей на нее плоской системы сил три уравнения равновесия:

Теперь рассмотрим равновесие угольника CDE (см. рис. 3.2, б) и составим для действующей на него плоской системы сил три уравнения равновесия:

По закону взаимодействия

Подставив в составленные уравнения числовые значения заданных величин, решаем систему уравнений (а) — (ж).

В итоге получим: N_c =N’_C = 40 кН, Х_А = 20 кН, У_А =—34,6 кН, Х_Е = = —46 кН, Y_e= 19,6 кН, т_Е = —9,32 кН • м. Знак минус, полученный для величин Y_a, Х_е, т_Е, указывает, что направления соответствующих воздействий противоположны показанным на рис. 3.2.

2. Рассмотрим решение задачи 3.1 (см. рис. 3.1) другим способом.

На первом этапе расчета рассмотрим равновесие всей конструкции целиком: не расчленяя систему тел в точке С, мысленно отделяем ее от внешних связей в точках А_и Е и показываем приложенные^ ней активные внешние воздействия F и М и реакции внешних связей X_A,Y_A, X_E,Y_E, т_Е (рис. 3.3).

Отметим, что система тел, освобожденная от внешних связей, не образует жесткой геометрически неизменяемой конструкции. Однако, в соответствии с принципом отвердевания ее рассматривают в качестве одного абсолютно твердого тела.

Принцип отвердевания: равновесие изменяемого тела (системы тел) не нарушается, если:

1) тело считать отвердевшим (абсолютно твердым);

2) каждое из тел системы считать абсолютно твердым, а соединения тел друг с другом считать абсолютно жесткими, так что совокупность тел образует одно твердое тело.

Для сил, действующих на систему тел (рис. 3.3), составляем три уравнения равновесия:

Полученные три уравнения содержат пять неизвестных Х_А, У_А, Х_Е, У* ‘Ид-

Второй этап решения — рассмотрение равновесия какого-нибудь одного тела системы, например балки АВ. Он полностью совпадает с соответствующей частью предыдущего решения, т. е. для действующей на балку АВ системы сил (см. рис. 3.2, а) составим уравнения равновесия (а) — (в). Решив полученную систему шести уравнений (а), (б), (в), (з), (и), (к), найдем все неизвестные.

Задача 3.2. Конструкция (рис. 3.4, а) состоит из бруса CD и угольника ЛВС, соединенных между собой шарниром в точке С и невесомым стержнем КЕ с шарнирами на концах; в точке А — подшипник, в точке D — опора на гладкую поверхность. К конструкции приложена пара сил с моментом М и силы, распределенные вдоль отрезка ВЛ по линейному закону, максимальная интенсивность которых q_m. Определить реакции в точках А, С, D и усилие в стержне КЕ, если известно М = 32 кН • м, q_m = 40 кН/м, а = 0,6 м, b = 0,5 м, с = 0,3 м, /= 0,4 м.

Решение. 1. Предварительно для удобства расчета действующую на участке ВА нагрузку в виде распределенных параллельных сил, модуль которых меняется по линейному закону, заменим равнодействующей Q, модуль которой и точку приложения L следует определить (рис. 3.4, б). Если отсчитывать z от точки В, значение q, соответствующее координате z, будет определено из пропорции q/z — q,J3l• Найдем модуль равнодействующей распределенных сил:

Точку приложения L равнодействующей силы Q можно определить, приравняв сумму моментов всех_элементарных сил qdz, например относительно точки В, моменту силы Q относительно этой же точки, т. е. применив теорему Вариньона: Ът_в(ц ? dz) — QBL. Имеем

Приравнивая друг другу правые части двух последних выражений, находим BL = q_m3r/(q_m3l/2.) = 21. _

Следовательно, линия действия равнодействующей Q проходит через «центр тяжести» треугольника нагрузки, который находится в точке пересечения его медиан [BL = (2/3)ВА = (2/3) • 31= 21.

2. Рассмотрим сначала равновесие всей конструкции, состоящей из двух тел (рис. 3.5, а).

Изображаем действующие на конструкцию внешние силы: пару сил с моментом М силу Q — равнодействующую нагрузки, распределенной по участку ВА реакцию R_D, перпендикулярную опорной плоскости; реакцию подшипника А, которую представим составляющими Х_А и Y_A.

Заметим, что при рассмотрении системы тел как единого тела силы взаимодействия между отдельными телами системы показывать не надо (они являются внутренними силами системы и взаимно уравновешиваются).

Для полученной плоской системы сил составляем три уравнения равновесия, причем выбираем такие, чтобы в каждое уравнение входило лишь одно неизвестное. Составим уравнения суммы моментов сил относительно точки А (в которой пересекаются линии действия неизвестных сил

Х_А и Y_A) и точки G (в которой пересекаются линии действия неизвестных Х_А и R_d), а также сумму проекций сил на ось х (проекции двух неизвестных сил Y_a, R _d на эту ось равны нулю):

Подставив в уравнения значения заданных величин, найдем R_D = 40 кН, У_А = -40 кН, Х_А = -24 кН.

3. Теперь рассмотрим равновесие бруса CD (рис. 3.5, б). На него действуют: пара сил с моментом М реакция внешней связи R_A; силы X_C,Y_C, передаваемые через шарнир С от элемента АВС; сила Т — воздействие стержня КЕ. Для этой плоской системы сил составим тоже три уравнения равновесия. Учитывая, что величина R_D определена, составим уравнения сумм моментов сил относительно точек С и Я (точки пересечения линий действия неизвестных сил) и суммы проекций сил на ось у:

В каждое из этих уравнений входит по одной неизвестной величине (Т, Х_с, Y_c). Это достигнуто соответствующим выбором уравнений равновесия.

Подставив в составленные уравнения числовые значения заданных величин, найдем искомые реакции.

Ответ: R_D = 40 кН, Х_А = -24 кН, Г_А=-40 кН, Т_ =_-1_5 кН, Х_с= —15 кН, У_с = —40 кН. Знаки указывают, что силы X_A,Y_A,T,X_C и Y_c направлены противоположно показанным на рис. 3.5.

Задача 3.3. Для подъема груза D с помощью гибкого троса используются ворот, двухступенчатый барабан и блок с подвижной осью С (рис. 3.6, а). У ворота, закрепленного в точке Л цилиндрическим шарниром, диск радиусом г и рукоятка ЛЕ длиной / образуют одно твердое тело. Трос от диска ворота уходит к барабану под углом а к горизонту. Радиусы ступеней барабана и R₂. Найти соотношение между модулем силы Р, прикладываемой к рукоятке, и весом Q поднимаемого груза D. Определить также реакцию шарнира Л.

Решение. 1. Расчленяем систему на отдельные тела (рис. 3.6, б). Изображаем силы, действующие на каждое тело.

Наряду с силами P,Q и реакциями внешних связей Х_А, Y_A,X_B, Y_B на тела будут действовать натяжения соответствующих участков троса причем S < = -S^. Sl=-S^,а численно S<= S_<, . б/ = S₄. Проводим координатные оси и рассматриваем равновесие каждого тела.

• 2. Рассмотрев равновесие тела D из уравнения = 0, получим ^ = Q. Из уравнений равновесия блока С с прилегающим к нему отрезком троса lF_ky = 0 и Хш_с(/^) = 0 получим S<= S_A = Q/2.
• 3. Теперь рассмотрим равновесие двухступенчатого барабана вместе с участками троса, намотанного на ej;o ободы. На него действует плоская система сил (рис. 3.6, 6) S₂, S₃, Х_в, Y_B, и известно, что S₂ — (2/2. Так как в задаче не требуется определить реакцию подшипника В, то составим уравнение

4. Рассмотрим равновесие рукоятки с_диском, образующих единое тело, под действием плоской системы сил Р, S₂, X_A,Y_A (здесь неизвестны величины Р, Х_А, Y_a). Составляем уравнения:

Теоретическая механика: Решебник Яблонского:
Плоская система сил (С1, С2, С3, С4, С5)

Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач по темам плоская система сходящихся сил и произвольная плоская система сил.

Видео:Основные определения статикиСкачать

Задание С.1. Определение реакций опор твердого тела

На схемах (рис. 1–4) показаны три способа закрепления бруса, ось которого – ломаная линия. Задаваемая нагрузка (см. табл. 1) и размеры (м) во всех трех случаях одинаковы.

Определить реакции опор для того способа закрепления бруса, при котором реакция, указанная в табл. 1, имеет наименьший модуль.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Видео:Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Задание С.2. Определение реакций опор и сил в стержнях плоской фермы

Определить реакции опор фермы от заданной нагрузки, а также силы во всех ее стержнях способом вырезания узлов. Схемы ферм показаны на рис. 7–9. Необходимые для расчета данные приведены в табл. 3.

Дополнительно определить в трех стержнях фермы силы от той же нагрузки способом Риттера (номера стержней указаны в табл. 3).

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Задание С.3. Определение реакций опор составной конструкции (система двух тел)

Конструкция состоит из двух частей. Установить, при каком способе соединения частей конструкции модуль реакции, указанной в табл. 5, наименьший, и для этого варианта соединения определить реакции опор, а также соединения С.

На рис. 17–19 показан первый способ соединения – с помощью шарнира С. Второй способ соединения – с помощью скользящей заделки, схемы которой показаны в табл. 6.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Видео:Равновесие вала. Реакции опорСкачать

Задание С.4. Определение реакций опор составной конструкции (система трех тел)

Найти реакции опор составной конструкции, состоящей из трех тел, соединенных в точке D. Схемы конструкций представлены на рис. 25–27 (размеры – в м), нагрузка указана в табл. 8. В вариантах 1–15, 21–30 составные части соединены с помощью шарниров, а в вариантах 16–20 – с помощью гладкой втулки малой длины.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Видео:Определение реакций опор твердого телаСкачать

Задание С.5. Равновесие сил с учетом сцепления (трения покоя)

Определить минимальное (в вариантах 1–20, 25, 26, 29, 30) или максимальное (в вариантах 21–24, 27, 28) значение силы P и реакции опор системы, находящейся в покое. Схемы вариантов представлены на рис. 32–34, а необходимые для расчета данные – в табл. 10.

В вариантах 1–20 сцепление (трение покоя) учесть только между тормозной колодкой и барабаном. В вариантах 21–30 учесть сцепление в двух опорных точках тела весом G.

📸 Видео

Теоретическая механика. Задание С1 (часть 9) из сборника ЯблонскогоСкачать

Теоретическая механика термех Статика Нахождение реакции связей часть 1Скачать

определение реакций в стержнях от действия грузовСкачать

Теоретическая механика. Задание С1 (часть 6) из сборника ЯблонскогоСкачать

Физика 10 класс (Урок№14 - Статика. Равновесие абсолютно твердых тел.)Скачать

Теоретическая механика термех Статика Нахождение реакции связей часть 2Скачать

Теоретическая механика. Задание С1 (часть 4) из сборника ЯблонскогоСкачать

Теоретическая механика. Задание С7 (часть 2) из сборника ЯблонскогоСкачать

Задача о составной конструкцииСкачать

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Теоретическая механика. Задание С1 (часть 8) из сборника ЯблонскогоСкачать