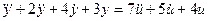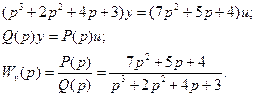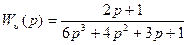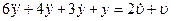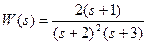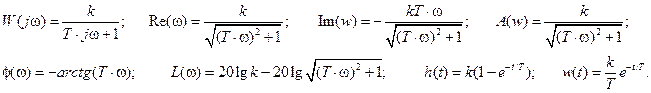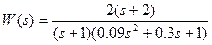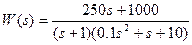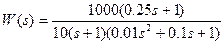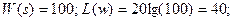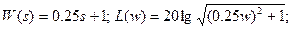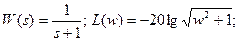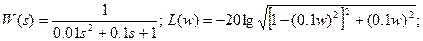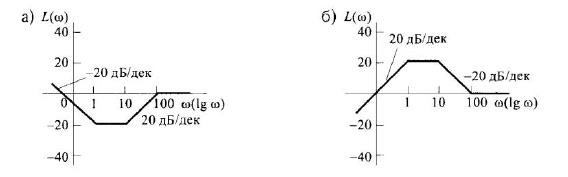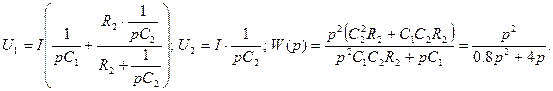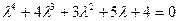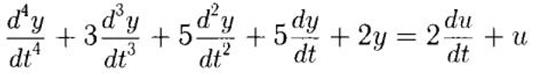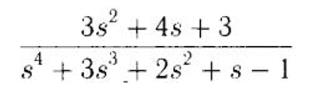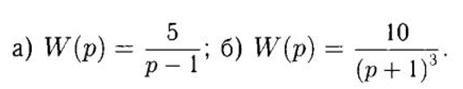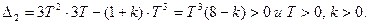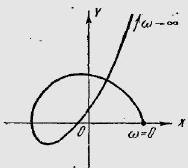Определить передаточную функцию системы и записать уравнение в разностной форме

по учебной дисциплине

«Теоретические Основы Управления»

Выполнил: магистрант группы МЭЭ-01-13/03

Нестерин Андрей Алексеевич

Проверил: доцент, к. т. н.

Мочалов Михаил Юрьевич

Чебоксары 2014 г.

1) Определить передаточную функцию в операторной форме системы управления, которая описываются следующим уравнением:

Передаточная функция в операторной форме будет иметь следующий вид:

2) Записать дифференциальное уравнение системы управления, передаточная функция которой имеет следующий вид:

Дифференциальное уравнение системы имеет вид:

3) Определить весовую и переходную функции для звена со следующей передаточной функцией:

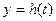
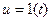
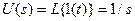
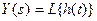
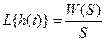
Из определения переходной функции следует, что при . Так как при этом и , то получаем

.

Переходная функция по теореме разложения:

.

.

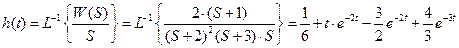
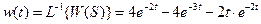
4) Определить частотную передаточную функцию, вещественную, мнимую, амплитудную, фазовую, логарифмическую амплитудную частотные функции, переходную и весовую функции апериодического звена.

.

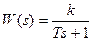
Его частотные и временные функции:

5) На вход системы подается сигнал u = 2×sin(0.5t). Определить в установившемся режиме реакцию системы со следующей передаточной функцией:

Изображение входного сигнала

.

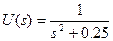
Изображение выходного сигнала

.

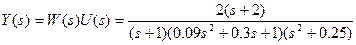
Установившееся значение оригинала:

.

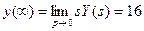
6) Построить асимптотическую ЛАЧХ звена со следующей передаточной функцией:

Для построения ЛАЧХ (рисунки 1,2) последовательного соединения звеньев следует построить соответствующие характеристики каждого звена, и затем геометрически их сложить:

a. Пропорциональное звено:

b. Форсирующее звено:

c. Апериодическое звено:

d. Колебательное звено:

7) Записать передаточные функции звеньев, если их асимптотические ЛАЧХ имеют следующий вид:

7)

a) ;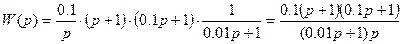

b) .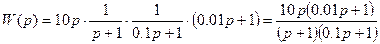

Рисунок 1 – Асимптотическая ЛАЧХ

Рисунок 2 – ЛАЧХ

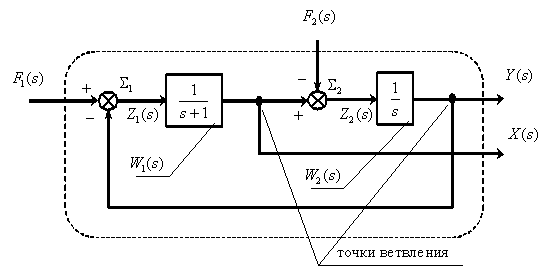
8) Для системы на рисунке определить следующие передаточные функции (ПФ):

а) Wyg — ПФ относительно входа g и выхода у,

б) Wyf — ПФ относительно входа f и выхода y.

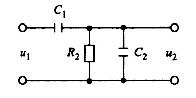
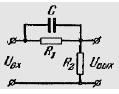
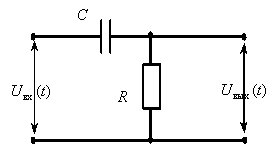
9) Составить передаточную функцию для пассивного четырехполюсника, показанного на рисунке:

C1 = 4 мкФ, R2 = 200 кОм, С2 = 1 мкФ.

10) Исследовать устойчивость системы управления, у которой характеристическое уравнение имеет следующий вид:

Корни характеристического уравнения:

11) Исследовать устойчивость системы управления, которая описывается следующим уравнением:

.

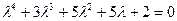
Корни характеристического уравнения:

12) Исследовать устойчивость замкнутой системы при следующей передаточной функции разомкнутой системы:

.

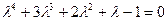
Корни характеристического уравнения:

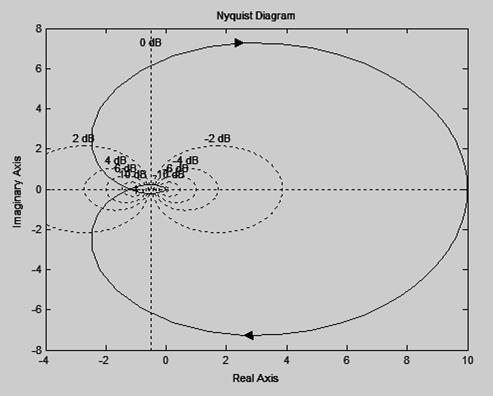
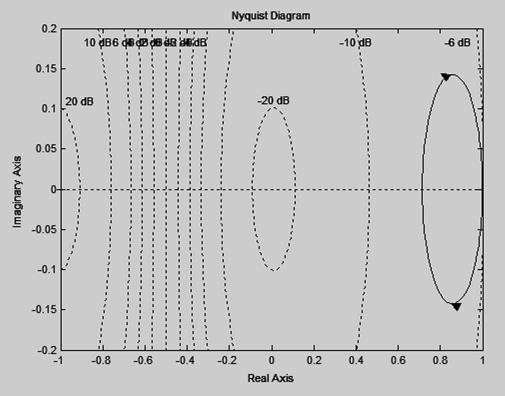
13) Пользуясь критерием Найквиста исследовать устойчивость замкнутой системы, если передаточная функция разомкнутой системы имеет вид:

a. Система имеет один правый нуль и АФЧХ (рисунок 3) 0,5 раз охватывает точку (-1; j0). Система устойчива.

Рисунок 3 – АФЧХ для варианта а)

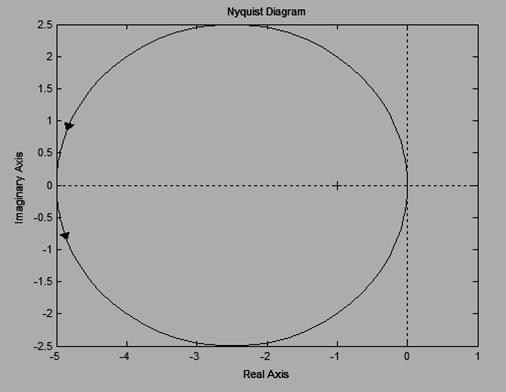
b. Система имеет один правый нуль и АФЧХ (рисунок 4) 1 раз охватывает точку (-1; j0). Система неустойчива.

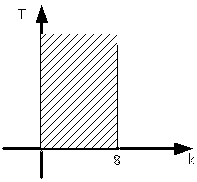
14) Передаточная функция разомкнутой системы W(p) = k/(Тр+ 1) 3 . Определить область устойчивости замкнутой системы на плоскости параметров (к,Т).

Характеристическое уравнение замкнутой системы:

.

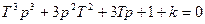
Система устойчива при T>0 и k>0, а также .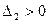

Рисунок 4 – АФЧХ для варианта б)

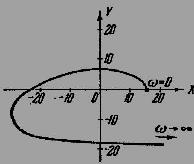
15) Найти уравнение кривой, представляющей собой амплитудно-фазовую характеристику дифференцирующего звена, изображенного на рисунке. Построить амплитудно-фазовую характеристику звена для случая R1 = 40 кОм, R2 = 10 кОм, С = 2,5 мкф.

.

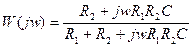
АФЧХ цепи построена на рисунке 5.

16) Система автоматического управления имеет характеристическое уравнение четвертого порядка. Кривая Михайлова системы приведена на рисунке. Определить устойчивость автоматической системы.

Рисунок 5 – АФЧХ дифференцирующего звена

17) Система автоматического управления имеет характеристическое уравнение пятого порядка. На рисунке приведена кривая Михайлова системы. Определить число корней характеристического уравнения с отрицательной вещественной частью и число корней характеристического уравнения с положительной вещественной частью.

2 корня с отрицательной вещественной частью и 1 корень с положительной вещественной частью.

Видео:proТАУ: 1. Передаточная функцияСкачать

Дифференциальные уравнения

Задача №1 дифференциальный уравнение функция

Записать дифференциальное уравнение системы управления с одним выходом и двумя входами и , передаточные функции которых имеют вид:

Система управления определяется двумя передаточными функциями:

1) передаточной функцией относительно входа :

2) передаточной функцией относительно входа :

С помощью передаточной функции уравнение рассматриваемой системы управления можно записать в виде:

Передаточные функции сложных систем легко могут быть определены через передаточные функции составляющих их элементов.

Имеющее наименьший порядок отношение изображений Лапласа выходной и входной переменных, вычисленных при нулевых начальных условиях, называется передаточной функцией в изображениях Лапласа. В соответствии с определением передаточная функция в изображениях Лапласа не может иметь равные между собой нули и полюса, так как в этом случае ее порядок может быть понижен путем сокращения числителя и знаменателя на общий множитель.

Так как оператор , то дифференциальное уравнение системы управления имеет вид:

На вход системы подается сигнал . Определить в установившемся режиме реакцию системы на входное воздействие при следующих передаточных функциях:

Рассмотрим, как определить в установившемся режиме реакцию системы, если известна ее передаточная функция

а на ее вход подается гармонический сигнал

Для этого перейдем от передаточной функции в изображениях Лапласа к частотной передаточной функции , произведя подстановку , где :

Частота подаваемого на вход системы сигнала . Произведем ее оценку:

Подставим значение частоты в формулу:

С учетом этого, согласно формуле, выходной сигнал системы в установившемся режиме имеет вид:

С помощью критерия Гурвица исследовать устойчивость систем управления, которые описываются следующими дифференциальными уравнениями ( — выход, — вход):

Для определения устойчивости линейной системы управления необходимо определить переходную составляющую. Для этого необходимо решить однородное дифференциальное уравнение

Необходимым условием устойчивости системы является условие положительности всех коэффициентов ее характеристического уравнения:

Алгебраические критерии устойчивости определяют условия устойчивости в виде алгебраических неравенств, составленных из коэффициентов характеристического уравнения системы.

Согласно алгебраическому критерию устойчивости Гурвица, для того чтобы система управления была устойчива необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительными.

Для системы управления четвертого порядка характеристическое уравнение имеет вид:

Составим определитель Гурвица 4-го порядка:

Если все коэффициенты характеристического уравнения положительны, то условия устойчивости по Гурвицу имеют вид:

Элементы последнего столбца определителя Гурвица, за исключением нижнего, будут равны нулю. Поэтому определитель Гурвица можно представить в виде:

Определитель Гурвица и все его диагональные миноры положительны, следовательно система устойчива.

С помощью критерия Михайлова исследовать устойчивость замкнутой системы управления, у которой передаточная функция в разомкнутом состоянии имеет вид:

Для анализа устойчивости замкнутой системы управления по ее передаточной функции в разомкнутом состоянии

вначале следует определить характеристическое уравнение замкнутой системы управления:

Затем производят подстановку в и находят выражение для характеристического вектора:

Далее определяют выражения для вещественной и мнимой частей:

После чего определяют значения частот, при которых кривая Михайлова пересекает мнимую ось. Для этого находят вещественные корни уравнения . Получаем:

Затем определяют значения частот, при которых кривая Михайлова пересекает вещественную ось. Для этого находят вещественные корни уравнения . Получаем:

После этого определяют координаты точек пересечения кривой Михайлова с осями координат. Результаты вычислений сводим в таблицу:

По полученным координатам точек строим кривую Михайлова. Анализируя расположение этой кривой на комплексной плоскости, видим, что она последовательно обходит против часовой стрелки квадранта, охватывая начало координат. Следовательно, исследуемая система 3-го порядка в замкнутом состоянии будет устойчива.

Рис. 1. Кривая Михайлова

Одноконтурная система управления содержит объект и пропорционально-интегральный регулятор (ПИ-регулятор), передаточные функции которых соответственно равны:

Определить оптимальные параметры настройки (коэффициент передачи) и (постоянная интегрирования) ПИ-регулятора, если даны:

— коэффициент передачи объекта;

— время транспортного запаздывания, с;

— постоянная времени объекта, с;

— порядок линейного дифференциального уравнения одномерной системы управления.

1. Для определения окрестности оптимальных параметров настройки

вычисляем границы этой окрестности:

Таким образом, (0,003; 3,925).

2. Для значений частоты = 0,0035; 0,004; 0,0045; 0,005 вычисляем длину вектора:

Для тех же значений частоты вычисляем угол между вектором и отрицательной мнимой полуосью, причём — угол между отрицательной вещественной полуосью и лучом ОЕ (рис.2) обычно на практике используют значения

Рис.2. КЧХ объекта и графическое задание величины

• 0,055
• 0,435
• 0,781

Определяем вспомогательную функцию по формуле:

Результаты вычислений сводим в таблицу:

Рис. 3. Настройка регулятора методом вспомогательной функции

3. Из таблицы определяем, что вспомогательная функция принимает максимальное значение при частоте = 0,004 c-1 и соответствующему этой частоте коэффициенту передачи

Тогда искомая постоянная интегрирования ПИ-регулятора

и оптимальное значение передаточной функции ПИ-регулятора имеет вид:

• 1. Автоматика: Основные понятия, терминология и условные обозначения: Справочное пособие / А.А. Герасенков, А.А. Шавров, О.А. Липа; Рос. гос. аграр. заоч. ун-т. — М., 2008.
• 2. Шавров А.В. Основы теории управления: учеб. пособие / А.В.Шавров, О.А.Липа, А.А.Шавров; Рос. гос. агр. заоч. ун-т. — М., 2005.
• 3. Бородин И.Ф., Судник Ю.А. Автоматизация технологических процессов. — М.: КолосС, 2004.
• 4. Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. — М.: Физматлит, 2007.
• 5. Солдатов В.В. Технические средства автоматизации: учеб. пособие / В.В.Солдатов, А.В.Шавров, А.А.Герасенков; Рос. гос. агр. заоч. ун-т. — М., 2004.
• 6. Радченко Г.Е. Автоматизация сельскохозяйственной техники: учеб. пособие. — Минск: УП «Технопринт», 2005.
• 7. Ротач В.Я. Теория автоматического управления: учебник для вузов. 2-е изд., перераб. и доп.- М.: Издательство МЭИ, 2004.

Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Определить передаточную функцию системы и записать уравнение в разностной форме

Понятие линейного динамического звена

САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов – динамических звеньев.

Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.

Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.

Если уравнение, связывающее сигналы и , линейно, то говорят о линейном динамическом звене

Уравнение линейного динамического звена имеет следующий общий вид:

где — постоянные коэффициенты, .

Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.

Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу

.

Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов

Преобразуем уравнение (2) к следующему виду

Получим из (3) отношение изображений выходного и входного сигналов

Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (), имеет вид дробно-рациональной функции.

Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена

.

,

называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции – это характеристический полином дифференциального уравнения, описывающего динамическое звено.

Определим передаточную функцию динамического звена по его принципиальной электрической схеме

По второму закону Кирхгоффа запишем уравнения описывающие схему

С учетом того, что

,

Получим операторные уравнения

Из второго уравнения выразим значение изображения тока

Подставим полученное выражение в первое уравнение системы

.

В итоге получаем искомую передаточную функцию

.

Графически передаточные функции динамического звена представляют в следующем виде:

Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях

.(5)

В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:

Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.

Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.

По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.

Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,

Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим

.

Тогда передаточная функция этого звена имеет вид

,

а выражение описывает суммирующее звено . Таким образом, получены два фрагмента структурной схемы

Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,

.

Тогда передаточная функция этого звена имеет вид

,

а выражение описывает суммирующее звено . Таким образом, получены еще два фрагмента структурной схемы

Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим

Временные характеристики динамического звена

Временной или импульсной характеристикой динамического звена называют реакцию звена на , обозначая ее как . При этом схема эксперимента имеет вид –

Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?

Для этого рассмотрим динамическое звено с передаточной функцией

В этом случае, в соответствии с (5), имеем

.

Получаем, что передаточная функция звена – это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции

,

при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.

Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.

Для динамического звена с передаточной функцией преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,

,

а если легко получить , тогда

.

Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на , обозначая ее как . При этом схема эксперимента имеет вид –

Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией

В этом случае, в соответствии с (5), имеем

.

По теореме об интегрировании оригинала имеем

Переходная функция является интегралом по времени от импульсной характеристике и наоборот

.

Переходная характеристика динамического звена может быть определена по передаточной функции

Контрольные вопросы и задачи

Что такое линейное динамическое звено?

Как определить передаточную функцию линейного динамического звена?

Перечислите основные элементы структурных схем систем управления.

Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?

Как по переходной характеристике определить импульсную характеристику динамического звена?

Определите передаточную функцию динамического звена по его принципиальной электрической схеме

.

Определите передаточную функцию динамического звена по его принципиальной электрической схеме

.

По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.

📺 Видео

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

6.3 Решение разностных уравненийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

c12 4, Дискретные системы: Z преобразованиеСкачать

Теория автоматического управления. Лекция 5. Дискретные САУ. Свойства передаточных функций ДСАУСкачать

Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Передаточные функцииСкачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Теория автоматического управления. Лекция 2. Дискретные САУ. Решетчатые функцииСкачать

Метод пространства состояний САУ: описание конкретной системыСкачать

Линейная функция, квадратичная функция и обратно-пропорциональная функция | Математика | TutorOnlineСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

ТФКП. Проверить условия Коши-Римана. Выяснить является ли функция аналитической.Скачать

Математический анализ, 5 урок, Непрерывность функцииСкачать

AGalilov: Преобразование Фурье "на пальцах"Скачать

Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать