Задача.Для заданного набора пар значений независимой переменной и функции определить наилучшие линейное приближение в виде прямой с уравнением у = ах + b и показательное приближение в виде линии с уравнением
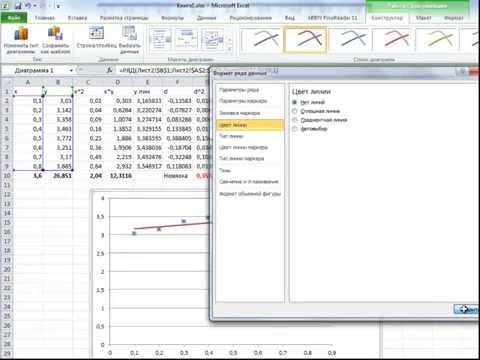
1. Запустите программу Excel (Пуск > Программы > Microsoft Excel) и откройте рабочую книгу book.xls, созданную ранее.
2. Щелчком на ярлычке выберите рабочий лист Обработка эксперимента.
3. Сделайте ячейку С1 текущей и щелкните на кнопке Изменить формулу в строке формул. Раскройте список на левом краю строки формул и выберите пункт Другие функции.
4. В окне мастера функций выберите категорию Ссылки и массивы и функцию ИНДЕКС. В новом диалоговом окне выберите первый вариант набора параметров.
5. Установите текстовый курсор в первое поле для ввода параметров в палитре формул и снова выберите пункт Другие функции в раскрывающемся списке в строке формул.
6. С помощью мастера функций выберите функцию ЛИНЕЙН категории Статистические.
7. В качестве первого параметра функции ЛИНЕЙН выберите диапазон, содержащий значения функции (столбец В).
8. В качестве второго параметра функции ЛИНЕЙН выберите диапазон, содержащий значения независимой переменной (столбец А).
9. Переместите текстовый курсор в строке формул, чтобы он стоял на имени функции ИНДЕКС. В качестве второго параметра функции ИНДЕКС задайте число 1. Щелкните на кнопке ОК на палитре формул.
Функция ЛИНЕЙН возвращает коэффициенты уравнения прямой в виде массива из двух элементов. С помощью функции ИНДЕКС выбирается нужный элемент.
10.Сделайте текущей ячейку D1. Повторите операции, описанные в пп. 3-9, чтобы в итоге в этой ячейке появилась формула: =ИНДЕКС(ЛИНЕЙН(В1 :В20;А1 :А20);2). Ее можно ввести и вручную (посимвольно). Теперь в ячейках С1 и D1 вычислены, соответственно, коэффициенты а и и уравнения наилучшей прямой.
11.Сделайте текущей ячейку С2. Повторите операции, описанные в пп. 3-9, или введите вручную следующую формулу:
12. Сделайте текущей ячейку D2. Повторите операции, описанные в пп. 3-9, или введите вручную следующую формулу:
=ИНДЕКС(ЛГРФПРИБЛ(В1 :В20;А1 :А20);2).
Теперь ячейки С2 и D2 содержат, соответственно, коэффициенты а и b уравнения наилучшего показательного приближения.
Для интерполяции или экстраполяции оптимальной кривой без явного определения ее параметров можно использовать функции ТЕНДЕНЦИЯ (для линейной зависимости) и РОСТ (для показательной зависимости).
13.Для построения наилучшей прямой другим способом дайте команду Сервис >
Анализ данных.
14.В списке Инструменты анализа выберите пункт Регрессия, после чего щелкните на кнопке ОК.
15.В поле Входной интервал Уукажите методом протягивания диапазон, содержащий значения функции (столбец В).
16.В поле Входной интервал X укажите методом протягивания диапазон, содержащий значения независимой переменной (столбец А).
17.Установите переключатель Новый рабочий лист и задайте для него имя Результат расчета.
18.Щелкните на кнопке ОК и по окончании расчета откройте рабочий лист Результат расчета. Убедитесь, что вычисленные коэффициенты (см. ячейки В17иВ18) совпали с полученными первым методом.
19.Сохраните рабочую книгу book.xls.
Мы научились анализировать с помощью программы Excel экспериментальные данные с использованием метода наименьших квадратов. Мы применили для вычислений разные средства программы Excel. Мы получили информацию, необходимую для построения графиков нужных приближений.
 |
Дата добавления: 2016-09-26 ; просмотров: 1343 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать
Линейная аппроксимация
При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.
Аппроксимацией (приближением) функции f(x) называется нахождение такой функции ( аппроксимирующей функции ) g(x) , которая была бы близка заданной. Критерии близости функций могут быть различные.
В случае если приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной .
В случае если аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной . Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.
Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.
Пусть задан дискретный набор точек, называемых узлами интерполяции , а также значения функции в этих точках. Требуется построить функцию g(x) , проходящую наиболее близко ко всем заданным узлам. Таким образом, критерием близости функции является g(xi)=yi .
В качестве функции g(x) обычно выбирается полином, который называют интерполяционным полиномом .
В случае если полином един для всей области интерполяции, говорят, что интерполяция глобальная .
В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.
Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию ).
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
Аппроксимация линейной функцией
Любая линейная функция может быть записана уравнением 
Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.
С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение: 
Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю. 
Решаем полученную систему уравнений 
Определяем значения коэффициентов 
Для вычисления коэффициентов необходимо найти следующие составляющие: 
Тогда значения коэффициентов будут определены как 
Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать
Пример реализации
Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой
y = 8 · x — 3
Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.
Реализация на Си
Видео:Парная регрессия: линейная зависимостьСкачать
Построение графика функции
Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.
Реализация на Си
Видео:Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать
Аппроксимация с фиксированной точкой пересечения с осью y
В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a. 
В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).
Видео:Математика #1 | Корреляция и регрессияСкачать
Наилучшее линейное приближение
Такие взаимосвязанные величины часто возникают на практике, например, доход и потребление в экономике, нагрузка сети и доход компании сотовой связи и т.д.
Поставим следующую задачу: найти наилучшее линейное приближение одной величины с помощью другой.
Итак, мы наблюдаем одну случайную величину и хотим спрогнозировать другую.
Пусть, для определенности, мы хотим приблизить значения величины 
значениями величины 
Иными словами, мы хотим найти линейную комбинацию вида 
(где 
и 
— неизвестные постоянные), дающие наилучшее приближение для случайной величины в том смысле, что
(*)
Минимум в правой части (*) берется по всем постоянным c1 и c2.
Такое приближение называется наилучшим среднеквадратическим приближением.
Оказывается, такое оптимальное приближение или прогноз одной величины по другой, действительно, можно найти.
Обратите внимание, что мы работаем только в классе линейных приближений и ищем наилучшее или оптимальное приближение в смысле (*).
Заметим также, мы не делаем никакого предположения о виде распределения случайных величин, а рассматриваем общий случай (важно, чтобы у величин существовало среднее и дисперсия).
Начнем проводить рассуждения.
1. Рассмотрим вначале простой случай, который позволяет прояснить суть дела.
Пусть случайная величина есть константа.
Наилучшим среднеквадратическим приближением для является, очевидно, среднее.
Это основано на том факте, что
2. Рассмотрим общий случай.
(**)
Где 
Перейдем для удобства к нормированным случайным величинам
и 
Для любых постоянных c1 и c2 имеем
Видно, что минимум выражения 
достигается, когда c1 = 0 и c2 = r:
Выражая разность 
через исходные величины и
И, очевидно, искомая линейная комбинация есть
Здесь a1 и a2 – математические ожидания случайных величин и 
и 
— их дисперсии, а определенная равенством (**) постоянная r – так называемый коэффициент корреляции этих случайных величин.
Видно, что коэффициент корреляции r всегда лежит в пределах 
есть просто линейная комбинация вида 
Действительно, если r=-1 или r=1, то
И, следовательно, 
с вероятностью 1.
Случайные величины и называют некоррелированными, если их коэффициент корреляции равен 0.
Отметим, что независимые величины являются некоррелированными, так как
Обратное, вообще говоря, неверно:
Из некоррелированности случайных величин не следует их независимость.
В частном случае гауссовских (нормальных) случайных величин, понятия некоррелированности и независимости совпадают.
📽️ Видео
Метод наименьших квадратов. Квадратичная аппроксимацияСкачать
Прогнозирование в Excel с помощью линий трендаСкачать
ПочЭкай ты меня называла 31Скачать
0801 Линейная аппроксимацияСкачать
Построение уравнения линейной регрессии методом наименьших квадратов.Скачать
Метод наименьших квадратов (МНК)Скачать
Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать
Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать
Линейная регрессияСкачать
Аппроксимация в ExcelСкачать
Метод Наименьших Квадратов (МНК)Скачать
Что такое линейная регрессия? Душкин объяснитСкачать
Метод наименьших квадратов. ТемаСкачать
Решение задачи линейного программирования при помощи надстройки Поиск решенияСкачать
