Статья раскрывает суть нормального (нормированного) уравнения и показывает, при каких видах задач его чаще всего применяют. Рассмотрим выведение нормального уравнения плоскости с примерами решений. Приведем примеры приведения общего уравнения плоскости к нормальному виду. Решим задачи по нахождению расстояния от точки до плоскости при помощи нормального уравнения плоскости.
- Нормальное уравнение плоскости – описание и пример
- Приведение общего уравнения плоскости к нормальному виду
- Нахождение расстояния от точки до плоскости
- Нормальное уравнение плоскости
- Приведение общего уравнения плоскости к нормальному виду
- 40. Нормальное уравнение плоскости. Расстояние от точки до плоскости
- 🎦 Видео
Видео:5. Нормальное уравнение плоскости выводСкачать

Нормальное уравнение плоскости – описание и пример
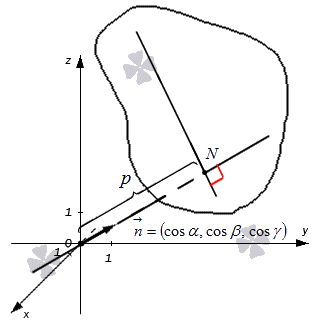
Возьмем прямоугольную систему координат О х у z трехмерного пространства. Если плоскость удалена на расстояние p ≥ 0 в положительном направлении нормального вектора n → . Возьмем за единицу длину вектора n → . Получим, что координатами направляющего косинуса являются n → = ( cos α , cos β , cos γ ) , тогда n → = cos 2 α , cos 2 β , cos 2 γ = 1 .
Примем обозначение O N за расстояние от точки до плоскости, таким образом, точка N принадлежит плоскости, где длиной отрезка O N будет значение p . Представим это на рисунке, изображенном ниже.
Теперь найдем уравнение заданной плоскости.
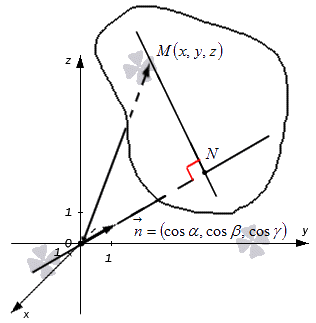
В трехмерном пространстве обозначим точку M ( x , y , z ) . Отсюда получим, что O M → , являющийся ее радиус вектором, с координатами ( x , y , z ) . Запись примет вид O M → = ( x , y , z ) . Отсюда получаем, что плоскость определена множеством точек M ( x , y , z ) , тогда числовая проекция вектора O M → по направлению n → равна значению p . Запись принимает вид n p n → O M → = p . Рассмотрим на приведенном ниже рисунке.
Из вышесказанного получим, что определение скалярного произведения векторов по формуле n → = ( cos α , cos β , cos γ ) и O M → = ( x , y , z ) в результате дают равенство
n → , O M → = n → · O M → · cos n ⇀ , O M → ^ = n → · n p n → O M → = 1 · p = p
Данная формула представляет скалярное произведение в координатной форме. Тогда получаем следующее выражение:
n → , O M → = cos α · x + cos β · y + cos γ · z
При сопоставлении двух последних равенств получаем уравнение плоскости такого вида cos α · x + cos β · y + cos γ · z = p . Упростим выражения. Для этого необходимо перенести значение p в левую сторону, получим cos α · x + cos β · y + cos γ · z — p = 0 .
cos α · x + cos β · y + cos γ · z — p = 0 называют нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Реже его называют нормированным уравнением заданной плоскости.
Теперь заданное в прямоугольной системе координат О х у z нормальное уравнение принимает вид cos α · x + cos β · y + cos γ · z — p = 0 . Р имеет значение расстояния положительного направления единичного нормального вектора плоскости n → = ( cos α , cos β , cos γ ) .
Чаще всего косинус не представляется явно в уравнении плоскости, потому как cos α , cos β и cos γ является некоторыми действительными числами, сумма квадратов которых равна единице.
Рассмотрим пример нормального уравнения плоскости.
Если имеется плоскость, заданная в прямоугольной системе координат O x y z при помощи уравнения нормального вида, — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 .
Отсюда cos α = — 1 4 , cos β = — 3 4 , cos γ = 6 4 .
Из выражения находим, что — 1 4 , — 3 4 , 6 4 — координаты нормального вектора плоскости n → . Его длина вычисляется из формулы n → = — 1 4 2 + — 3 4 2 + 6 4 2 = 1 . Плоскость располагается относительно координат в направлении вектора n → на расстоянии 7 единиц, потому как p = 7 .
Отсюда ясно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости A x + B y + C z + D = 0 , где A , B , C – некоторые действительные числа, при которых длина нормального вектора плоскости n → = ( A , B , C ) равняется 1 , причем D является неотрицательным числом.
Чтобы выявить, является представленное уравнение нормальным уравнением плоскости, необходимо выполнение обоих условий n → = cos 2 α + cos 2 β + cos 2 γ = 1 и p ≥ 0 , тогда получим уравнение плоскости нормального вида. При невыполнении хотя бы одного условия, уравнение не является нормальным.
Рассмотрим на примере.
Выявить уравнение плоскости нормального вида из заданных уравнений:
1 7 x — 4 7 y + 4 2 7 — 3 = 0 1 3 x + 7 6 y — 5 6 z + 2 5 = 0 1 3 x + 1 2 y + 1 4 z — 11 = 0
Начнем решение с первого уравнения. Для этого необходимо проверить, равняется ли длина нормального вектора n → = 1 7 , — 4 7 , 4 2 7 единице.
Вычисляем длину по формуле и получаем: n → = 1 7 2 + — 4 7 2 + 4 2 7 2 = 1 49 + 16 49 + 32 49 = 1
Необходимо поработать с числом p , так как его значение должно быть положительным. Это верно, так как p = 3 . Значит, первое заданное уравнение плоскости можно считать уравнением плоскости в нормальном виде.
Второе уравнение из заданных нельзя считать нормальным уравнением плоскости, так как условие p ≥ 0 не выполняется, ибо в данном уравнении p = — 2 5 .
Третье уравнение имеет нормальный вектор с координатами n → = 1 3 , 1 2 , 1 4 , длина которого не равняется единице из вычислений:
n → = 1 3 2 + 1 2 2 + 1 4 2 = 1 9 + 1 4 + 1 16 = 61 12 ≠ 1
Отсюда следует, что его нельзя считать за уравнение плоскости в нормальном виде.
Ответ: 1 7 x — 4 7 y + 4 2 7 z — 3 = 0 уравнение является нормальным уравнением плоскости.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Приведение общего уравнения плоскости к нормальному виду
Для приведения уравнения плоскости A x + B y + C z + D = 0 к нормальному виду, обе части умножаются на нормированный множитель ± 1 A 2 + B 2 + C 2 . Знак определятся по числу D , он должен быть противоположным значения числа D .
Когда D = 0 , знак может быть любым.
Нормальным уравнением плоскости считается общее уравнение плоскости после умножения на нормирующий множитель, потому как длина вектора с кооординатами ± A A 2 + B 2 + C 2 , ± B A 2 + B 2 + C 2 , ± C A 2 + B 2 + C 2 равна 1 .
Отсюда получаем, что ± A A 2 + B 2 + C 2 , ± B A 2 + B 2 + C 2 , ± C A 2 + B 2 + C 2 = A 2 + B 2 + C 2 A 2 + B 2 + C 2 = 1 .
Знак множителя необходим для того, что проверять выполнимость условия p ≥ 0 .
Привести уравнение 2 x — 3 y + z + 5 = 0 к нормальному виду.
Из условия имеем, что A = 2 , B = — 3 , C = 1 , D = 5 . Исходя из того, что D является положительным числом, нормирующий множитель дожжен иметь противоположный знак. Отсюда получим, что получим отрицательный результат.
— 1 A 2 + B 2 + C 2 = — 1 2 2 + ( — 3 ) 2 + 1 2 = — 1 14
Чтобы получить искомое нормальное уравнение плоскости, обе части уравнения необходимо умножить на нормирующий множитель. Получим:
— 1 14 · 2 x — 3 y + z + 5 = — 1 14 · 0 ⇔ ⇔ — 2 14 x + 3 14 y — 1 14 z — 5 14 = 0
Ответ: — 2 14 x + 3 14 y — 1 14 z — 5 14 = 0 .
Написать нормальное уравнение плоскости, если оно задано уравнением 3 x — 4 z = 0 прямоугольной системы координат O x y z .
Из условия видно, что A = 3 , B = 0 , C = — 4 , D = 0 . Знака перед множителем нет, потому как D = 0 . Значит, возьмем со знаком « + ». Получаем выражение вида:
1 A 2 + B 2 + C 2 = 1 3 2 + 0 2 + ( — 4 ) 2 = 1 5
При умножении обеих частей уравнения на нормирующий множитель, получаем уравнение плоскости нормального вида 3 5 x — 4 5 z = 0 .
Ответ: 3 5 x — 4 5 z = 0 .
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Нахождение расстояния от точки до плоскости
Теперь раскроем тему нормального уравнения плоскости, где уравнение плоскости нормального вида применимо для нахождения расстояния от заданной точки в пространстве до плоскости.
При заданной системе координат О х у z трехмерного пространства имеем плоскость с уравнением cos α · x + cos β · y + cos γ · z — p = 0 , где необходимо определить расстояние от p до точки M 0 ( x 0 , y 0 , z 0 ) заданной плоскости. Его вычисляют по формуле p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p . Само расстояние является числом, которое получается при подстановке координат точки в левую сторону уравнения. Для вывода формулы необходимо обратиться к статье расстояния от точки до плоскости.
Имеется уравнение плоскости вида — 1 3 x + 2 3 y — 2 3 z — 1 = 0 , которое располагается в прямоугольной системе координат. Определить расстояние от точки с координатами M 0 ( 1 , — 3 , 0 ) до плоскости.
Координаты точки M необходимо подставить в левую часть уравнения плоскости. Тогда получаем:
— 1 3 · 1 + 2 3 · ( — 3 ) — 2 3 · 0 — 1 = 0
Искомое расстояние – величина абсолютная, значит p = — 3 1 3 = 3 1 3 .
Если плоскость задана другим уравнением, а необходимо произвести вычисление от заданной точки до плоскости, необходимо привести уравнение к виду нормального уравнения плоскости, используя формулу p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p .
Найти расстояние от заданной точки с координатами M 0 ( 5 , — 1 , 2 ) до плоскости x 5 + y — 2 + z 4 = 1 .
По условию имеем уравнение плоскости в отрезках. Это значит, что необходимо привести его к нормальному уравнению плоскости. Для этого переходим к общему уравнению, после чего приведем к нормальному виду.
Получаем: x 5 + y — 2 + z 4 = 1 ⇔ 1 5 x — 1 2 y + 1 4 z — 1 = 0
Для вычисления нормирующего множителя применяем: 1 1 5 2 + — 1 2 2 + 1 4 2 = 1 141 25 · 16 = 20 141
Обе части уравнения 1 5 x — 1 2 y + 1 4 z — 1 = 0 умножаем на нормирующий множитель. Теперь получено нормальное уравнение исходной плоскости вида:
4 141 x — 10 141 y + 5 141 z — 20 141 = 0
Отсюда видно, что cos α = 4 141 , cos β = — 10 141 , cos γ = 5 141 , p = — 20 141 , x 0 = 5 , y 0 = — 1 , z 0 = 2
Все имеющиеся данные помогут использовать формулу для нахождения искомого расстояния от точки до плоскости:
p = cos α · x 0 + cos β · y 0 + cos γ · z 0 — p = 4 141 · 5 — 10 141 · — 1 + 5 141 · 2 — 20 141 = 20 141
Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать

Нормальное уравнение плоскости
В данной статье мы рассмотрим нормальное уравнение плоскости. Приведем примеры построения нормального уравнения плоскости по углу наклона нормального вектора плоскости от осей Ox, Oy, Oz и по расстоянию r от начала координат до плоскости. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть в пространстве задана декартова прямоугольная система координат. Тогда нормальное уравнение плоскости Ω представляется следующей формулой:
| xcosα+ycosβ+zcosγ−r=0, | (1) |
где r− расстояние от начала координат до плоскости Ω, а α,β,γ− это углы между единичным вектором n, ортогональным плоскости Ω и координатными осьями Ox, Oy, Oz, соответственно (Рис.1). (Если r>0, то вектор n направлен в сторону плоскости Ω, если же плоскость проходит через начало координат, то направление вектора n выбирается произвольной).
Выведем формулу (1). Пусть в пространстве задана декартова прямоугольная система координат и плоскость Ω (Рис.1). Проведем через начало координат прямую Q, перпендикулярную плоскости Ω, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 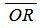
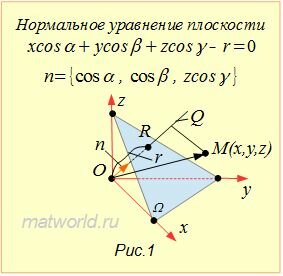 |
Выразим уравнение плоскости Ω через следующие параметры: длину отрезка 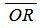
Так как вектор n является единичным вектором, то его проекции на Ox, Oy, Oz будут иметь следующие координаты:
| n=<cosα, cosβ, cosγ>. | (2) |
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M (x,y, z). Точка M лежит на плоскости Ω тогда и только тогда, когда проекция вектора 
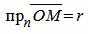 | (3) |
Скалярное произведение векторов n и 
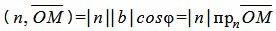 , , | (4) |
где 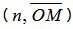


Поскольку n единичный вектор, то (4) можно записать так:
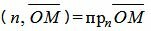 . . | (5) |
Учитывая, что n=<cosα, cosβ, cosγ>, 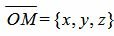
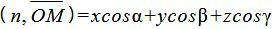 . . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosα+ycosβ+zcosγ=r, |
| xcosα+ycosβ+zcosγ−r=0. | (7) |
Мы получили нормальное уравнение плоскости Ω. Уравнение (7) (или (1)) называется также нормированным уравнением плоскости . Вектор n называется нормальным вектором плоскости .
Как было отмечено выше, число r в уравнении (1) показывает расстояние плоскости от начала координат. Поэтому, имея нормальное уравнение плоскости легко определить расстояние плоскости от начала координат. Для проверки, является ли данное уравнение плоскости уравнением в нормальном виде, нужно проверить длину нормального вектора этой плоскости и знак числа r, т.е. если |n|=1 и r>0, то данное уравнение является нормальным (нормированным) уравнением плоскости.
Пример 1. Задано следующее уравнение плоскости:
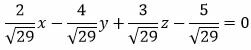 . . | (7) |
Определить, является ли уравнение (7) нормальным уравнением плоскости и если да, то определить расстояние данной плоскости от начала координат.
Решение. Нормальный вектор плоскости имеет следующий вид:
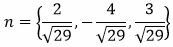 |
Определим длину вектора n:
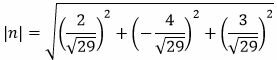 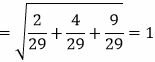 |
Ответ: Длина вектора n равна 1, 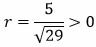
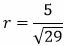
Видео:Видеоурок "Уравнение плоскости в отрезках"Скачать

Приведение общего уравнения плоскости к нормальному виду
| Ax+By+Cz+D=0. | (8) |
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Утрерждение 2 статьи «Общее уравнение плоскости»), то существует такое число t, что
| tA=cosα, tB=cosβ, tC=cosγ, tD=−r. | (9) |
Возвышая в квадрат первые три равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 +(tС) 2 =cos 2 α+cos 2 β+cos 2 γ=1. | (10) |
Упростим выражение и найдем t:
| t 2 A 2 +t 2 B 2 +t 2 C 2 =t 2 (A 2 +B 2 +C 2 )=1, |
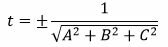 . . | (11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B, C не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на четвертое равенство в (9). Так как r−это расстояние от начала координат до плоскости, то r≥0. Тогда произведение tD должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку D.
Подставляя в (1) вместо cosα, cosβ, cosγ и −r значения из (9), получим tAx+tBy+tCz+tD=0. Т.е. для приведения общего уравенения плоскости к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение плоскости
| 2x−3y+6z+4=0. | (12) |
Построить нормальное уравнение плоскости (12).
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=6, D=4. Вычислим t из равенства (11):
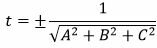 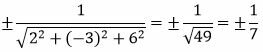 . . |
Так как D>0, то знак t отрицательный:
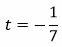 . . |
Умножим уравнение (12) на t:
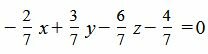 . . |
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
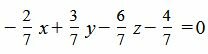 . . |
Отметим, что число 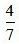
Видео:Видеоурок "Нормальное уравнение прямой"Скачать

40. Нормальное уравнение плоскости. Расстояние от точки до плоскости
40. Нормальное уравнение плоскости.
Расстояние от точки до плоскости.
Нормальным уравнением плоскости называется её уравнение, написанное в виде
где cos α, cos β, cos g суть направляющие косинусы нормали плоскости, р — расстояние до плоскости от начала координат. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).
Пусть М* — какая угодно точка пространства, d — расстояние от неё до данной плоскости. Отклонением о точки М* от данной плоскости называется число + d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число — d, если они лежат по одну сторону от данной плоскости (если М* лежит на самой плоскости, то отклонение равно нулю).
Если точка М* имеет координаты x*, у*, z*, а плоскость задана нормальным уравнением
x cos α + y cos β + z cos g— p = 0, то отклонение точки М* от этой плоскости даётся формулой
Общее уравнение плоскости
приводится к нормальному виду (1) умножением на нормирующий множитель, определяемый формулой

знак нормирующего множителя берётся противоположным знаку свободного члена нормируемого уравнения.
956. Определить, какие из следующих уравнений плоскостей являются нормальными:
1) 





3) 





5) 



7) 



11) – y —2 = 0; 12) z —5 = 0.
957. Привести каждое из следующих уравнений плоскостей к нормальному виду:
1) 2х —2у + 2 —18 = 0; 2) х — у —z 
3) 4х — 6у — 12z — 11=0; 4) — 4x — 4у + 2z + 1 =0;
7) у + 2 = 0; 8) —х + 5 = 0;
9) — z + 3 = 0; 10) 2z — 1= 0.
958. Для каждой из следующих плоскостей вычислить углы α, β и g, образуемые нормалью с осями координат, и расстояние р от начала координат:
1) х + у

3) х + z —6 = 0; 4) у — z + 2 = 0; 5) х
6) z— 2 = 0; 7) 2х + 1 = 0; 8) 2у + 1=0;
959. Вычислить величину отклонения 
1) М1 (—2; — 4; 3), 2х— у + 2z + 3 = 0;
2) М2 (2; — 1; — 1), 16х—12у + 15г —4 = 0;
3) М3 (1; 2; — 3), 5х—3у+ z+4 = 0;
4) М4 (3; —6; 7), 4х — 3z— 1=0;
5) М5 (9; 2; —2), 12у —5z + 5 = 0.
960. Вычислить расстояние d от точки Р (—1; 1; —2) до плоскости, проходящей через три точки М1 (1; —1; 1), М2 (—2, 1; 3) и М3(4; —5; —2).
961. Определить, лежат ли точка Q(2; — 1; 1) и начало координат по одну или по разные стороны относительно каждой из следующих плоскостей:
5) 2х + 3у —6z + 2 = 0; 6) 3х — 2у + 2z — 7 = 0.
962. Доказать, что плоскость 3х — 4у — 2z + 5 = 0 пересекает отрезок, ограниченный точками M1 (3; —2; 1) и M2 (—2; 5; 2).
963. Доказать, что плоскость 5х — 2у + z — 1= 0 не пересекает отрезка, ограниченного точками M1 (1; 4; —3) и M2 (2; 5; 0).
964. В каждом из следующих случаев вычислить расстояние между параллельными плоскостями:
1) х — 2у — 2z— 12 = 0, 2) 2х—3у + 6z—14 = 0,
х — 2у — 2z — 6 = 0; 4х —6у + 12z + 21 =0;
3) 2х — y + 2z + 9 = 0, 4) 16х + 12у — 15г + 50 = О,
4х —2у + 4z —21=0; 16х+ 12у — 15z + 25 = 0;
5) 30х — 32у + 24z—75=0, 6) 6х—18у—9z —28 = 0,
15х — 16у + 12z—25 = 0; 4х—12у—6г— 7 = 0.
965. Две грани куба лежат на плоскостях
2х —2у + 2—1=0, 2х —2у + z + 5 = 0.
Вычислить объём этого куба.
966. На оси Оу найти точку, отстоящую от плоскости х + 2у— 2z— 2 = 0 на расстоянии d = 4.
987. На оси Oz найти точку, равноудалённую от точки М(1; —2; 0) и от плоскости 3х — 2у + 6z — 9 = 0.
968. На оси Ох найти точку, равноудалённую от двух плоскостей:
12х—16у+15z+1=0, 2х + 2у — г— 1=0.
969. Вывести уравнение геометрического места точек, отклонение которых от плоскости 4х — 4у — 2z + 3 = 0 равно 2.
970. Вывести уравнение геометрического места точек, отклонение которых от плоскости 6х + 3у + 2z—10 = 0 равно —3.
971. Составить уравнения плоскостей, параллельных плоскости 2х—2у—z — 3 = 0 и отстоящих от неё на расстоянии d=5.
972. В каждом из следующих случаев составить уравнение геометрического места точек, равноудалённых от двух параллельных плоскостей:
973. В каждом из следующих случаев составить уравнения плоскостей, которые делят пополам двугранные углы, образованные двумя пересекающимися плоскостями:
1) х — 3у + 2z — 5 = 0, 2) 5х — 5у — 2z — 3 = 0,
3х —2у — z + 3 = 0; х + 7у —2z + 1=0;
3) 2х— у + 5z + 3 = 0, 2х— 10у + 4z — 2 = 0.
974. В каждом из следующих случаев определить, лежат ли точка M 1 (2; —1; 3) и начало координат в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
1) 2х—у + 32 — 5 = 0, 2) 2х + 3у — 5z — 15 = 0,
3х + 2у —z+3 = 0; 5х—у —3z —7 = 0;
3) х + 5у —z +1 = 0, 2х+17у + z + 2 = 0.
975. В каждом из следующих случаев определить, лежат ли точки М(2; —1; 1) и N (1; 2; —3) в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
1) 3х—у + 2z —3 = 0, 2) 2х—у + 5z—1=0,
х — 2у —z + 4 = 0; 3х —2у +6z—1=0.
976. Определить, лежит ли начало координат внутри острого или тупого угла, образованного двумя плоскостями: х — 2у + 3z — 5 = 0, 2х —у —z + 3 = 0.
977. Определить, лежит ли точка М(3; 2; —1) внутри острого или тупого угла, образованного двумя плоскостями: 5х—у + z + 3 = 0, 4х — 3у + 2z +5 = 0.
978. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2х—14у + 6z – 1 =0, 3х + 5у — 5z + 3 = 0, в котором лежит начало координат.
979. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2х—у + 22 — 3 = 0, 3х + 2у — 6z —1=0, в котором лежит точка М(1; 2; —3).
980. Составить уравнение плоскости, которая делит пополам острый двугранный угол, образованный двумя плоскостями: 2х — 3у — 42 — 3 = 0, 4х — 3у — 2z — 3 = 0.
981. Составить уравнение плоскости, которая делит пополам тупой двугранный угол, образованный двумя плоскостями: 3х — 4у — z + 5=0, 4х —3 у + z +5 = 0.
🎦 Видео
Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

Уравнение плоскости через 3 точкиСкачать

9 класс, 5 урок, Уравнение линии на плоскостиСкачать

§42 Нормальное урaвнение плоскостиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

§13 Нормальное уравнение прямойСкачать

Видеоурок "Нормальное уравнение плоскости"Скачать

Уравнение плоскости. 11 класс.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Уравнение окружности (1)Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать