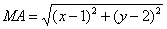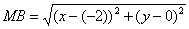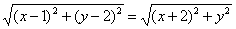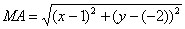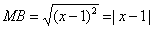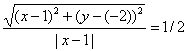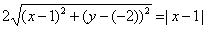Определить и построить множество точек удовлетворяющих данным уравнениям или неравенствам (3 видео)

Решение неравенств с комплексными переменными

Рассмотрим задачи на нахождение областей в комплексной плоскости, заданных неравенствами. Чтобы решить данные неравенства с комплексными числами, вначале необходимо перейти к декартовым координатам, т.е. перейти к действительному представлению.

Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z действительными переменными x и y, а именно z = x + iy, где
x = Re(z), y = Im(z).

Пример 1. Найти на комплексной плоскости множество точек, удовлетворяющих неравенству

Видео:Построение областей по заданным условиямСкачать

Определить и построить множество точек удовлетворяющих данным уравнениям или неравенствам

Пример 15. Построим множество точек ( x , y ) (x, y) , удовлетворяющих уравнению x 2 + x y = 0 x^2 + xy = 0 .

Построим множество точек ( x , y ) (x, y) таких, что

x 2 + 4 x + 4 + 4 y 2 = 0 x^2 + 4x + 4 + 4y^2 = 0 .

Аналогично рассматривается следующий пример, в котором также существенно выделение полного квадрата.

т. е. уравнению снова будет удовлетворять единственная точка ( 0,5 ; – 0,5 ) (0,5; – 0,5) (см. рис. 39).

Множеством точек может быть область на плоскости. Рассмотрим пример.

Построим множество точек ( x , y ) (x, y) таких, что

Покажем ещё пример построения множеств точек, удовлетворяющим уравнениям с модулями.

Построим множество точек, удовлетворяющих | y | = | x | |y| = |x| .

Видео:Изображение множества точек на координатной плоскости, удовлетворяющих уравнению.Скачать

Множество точек на плоскости

Пример №1 . Составить уравнение множества точек на плоскости, равноудаленных от точек A(1;2) и B(-2;0).
Решение
Пусть точка М принадлежит искомому множеству точек, тогда МА=МВ. Так как

то

После возведения левой и правой частей в квадрат и упрощений получим:
(x-1) 2 + (y-2) 2 = (x + 2) 2 + y 2
x 2 — 2x + 1 + y 2 — 4y + 4 = x 2 + 4x + 4 + y 2
или
— 6x — 4y + 1 = 0
Ответ: — 6x — 4y + 1 = 0.

Пример №2 .
Составить уравнение множества точек на плоскости, отношение расстояний которых от точки A(1;-2) и от прямой x=1 равно 1 /₂.
Решение
Из условия следует, что для любой точки M(x;y) искомого множества справедливо соотношение MA:MB = 1 /₂. Так как:

то

или

Возведя левую и правую части в квадрат и упрощая, получим:
4(x — 1) 2 + 4(y + 2) 2 = |x — 1| 2
т.е.
4(x 2 — 2x + 1) + 4(y 2 + 4y + 4) = x 2 — 2x + 1
или
3x 2 + 4y 2 — 6x +16y +19 = 0
Ответ: 3x 2 + 4y 2 — 6x +16y +19 = 0.

Пример №3 . Составить уравнение линий, если расстояние каждой ее точки А(2,0) относится к расстоянию до прямой 5x+8=0 как 5:4 .
Решение. Выражаем x = -8/5. λ=5/4. Подставляем данные в задание №2.

Пример №4 . Составить уравнение линии, каждая точка которой равноудалена от прямой x+6=0 и от начала координат.
Примечание. Здесь x=-6 , λ=1.