Определить число вещественных корней уравнения и отделить эти корни (6 видео)

3.1. Отделение корней нелинейного уравнения

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)

Верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

, (3.3)

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то

= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x+≤.

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

и .

≤x–≤ = =.

Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3×8 – 5×7 – 6×3 – x – 9 = 0

K = 1 B = |– 9| an = 3

= 4

9×8 + x7 + 6×5 + 5x – 3 = 0

Определить число вещественных корней уравнения и отделить эти корни

k = 8 B = 3 an = 9

Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4

3×8 + 5×7 + 6×3 + x – 9 = 0

9×8 – x7 – 6×5 – 5x – 3 = 0

K = 1 B = 6 an = 9

Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.

Рис. 3.1 Отделение корней на графике f(x).

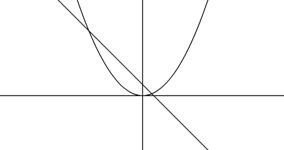
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

На графике 2 корня.

Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Содержание

Применение производной для решения нелинейных уравнений и неравенств
п.1. Количество корней кубического уравнения
п.2. Количество корней произвольного уравнения
п.3. Решение неравенств с построением графиков
Будь умным!
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Модифицированный метод Ньютона
ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ.
📸 Видео

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Применение производной для решения нелинейных уравнений и неравенств

п.1. Количество корней кубического уравнения

Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_=frac<-2bpmsqrt>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.

Пример 1. Сколько корней имеют уравнения:

1) (x^3+3x^2-4=0) (b^2-3ac=9gt 0 (c=0) ) (f(x)=x^3+3x^2-4 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-4, f(x_2)=0 ) (f(x_1)cdot f(x_2)=0Rightarrow) два корня	2) (x^3+3x^2-1=0) (b^2-3ac=9gt 0 ) (f(x)=x^3+3x^2-1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-1, f(x_2)=3 ) (f(x_1)cdot f(x_2)lt 0Rightarrow) три корня
3) (x^3+3x^2+1=0) (b^2-3ac=9gt 0) (f(x)=x^3+3x^2+1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=1, f(x_2)=5 ) (f(x_1)cdot f(x_2)gt 0Rightarrow) один корень	4) (x^3+x^2+x+3=0) (b^2-3ac=1-3lt 0 ) Один корень

п.2. Количество корней произвольного уравнения

Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.

Пример 2. а) Найдите число корней уравнения (frac 1x+frac+frac)
б) Найдите число корней уравнения (frac 1x+frac+frac=k)

Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac+frac $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac+fracright)=-infty-1-frac13=-infty\ lim_left(frac1x+frac+fracright)=+infty-1-frac13=+infty\ lim_left(frac1x+frac+fracright)=1-infty-frac12=-infty\ lim_left(frac1x+frac+fracright)=1+infty-frac12=+infty\ lim_left(frac1x+frac+fracright)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac+fracright)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac+fracright)=-0-0-0=-0\ lim_left(frac1x+frac+fracright)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac-frac-fraclt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.

5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.

6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)

7) График

Получаем ответ для задачи (а) 3 корня.

Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня

Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.

Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt=a $$ имеет по крайней мере одно решение.

Исследуем функцию (f(x)=sqrt+sqrt)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt=2sqrt, f(5)=sqrt+0=2)
Первая производная: begin f'(x)=frac<2sqrt>+frac<2sqrt>=frac<2sqrt>-frac<sqrt>\ f'(x)=0 text 2sqrt=sqrtRightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt+sqrt=sqrt+sqrt<frac>=frac<sqrt>=2sqrt end Промежутки монотонности:

(x)	1	(1; 7/3)	7/3	(7/3; 5)	5
(f'(x))	∅	+	0	—	∅
(f(x))	(2sqrt)	(nearrow )	max (2sqrt)	(searrow )	2

Можем строить график:

(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:

$$ alt 2 $$	нет решений
$$ 2leq alt 2sqrt $$	1 решение
$$ 2sqrtleq alt 2sqrt $$	2 решения
$$ a=2sqrt $$	1 решение
$$ agt 2sqrt $$	нет решений

По крайней мере одно решение будет в интервале (2leq aleq 2sqrt).

п.3. Решение неравенств с построением графиков

Пример 4. Решите неравенство (fracgt frac)

Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)

Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac end \ begin 0lt xlt 1\ 2+log_3 xltfrac end end right. \ 2+log_3 xgt fracRightarrow log_3 xgt fracRightarrow log_3 xgt frac\ left[ begin begin xgt 1\ log_3 xgtfrac end \ begin 0lt xlt 1\ log_3 xltfrac end end right. end Исследуем функцию (f(x)=frac=frac=1-frac)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-fracright)=1-frac=+infty\ lim_left(1-fracright)=1-frac=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-fracright)=1-frac=1+0\ lim_left(1-fracright)=1-frac=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-fracright)’=fracgt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac $$ Одна критическая точка 2-го порядка (x=frac12)

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Будь умным!

Работа добавлена на сайт samzan.net: 2016-06-20

Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.

ЛАБОРАТОРНАЯ РАБОТА №8

Видео:Как считать корни? #shortsСкачать

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

» xml:lang=»ru-RU» lang=»ru-RU»> Отделение корней

Отделить корень уравнения

значит найти такой отрезок области определения функции f ( x ), который содержит только один корень этого уравнения.

Для отделения корней уравнения (8.1) можно использовать следующий критерий: если на отрезке [ a , b ] функция f ( x ) непрерывна и монотонна, а её значения на концах отрезка имеют разные знаки, то на этом отрезке существует и при том только один корень данного уравнения. Достаточным признаком монотонности функции f ( x ) на отрезке [ a , b ] является сохранение знака производной. При отделении корней стараются определить отрезок как можно меньшей длины.

Отделение корней уравнения (8.1) можно выполнить также графически. Найти корень уравнения (8.1) значит найти абсциссу точки пересечения графика функции f ( x ) c осью абсцисс. Если построить график функции f ( x ) затруднительно, то уравнение (8.1) следует представить в эквивалентном виде

f 1 ( x )= f 2 ( x ) (8.2)

с таким расчетом, чтобы графики функций f 1 ( x ), f 2 ( x ) строились проще. Корни же уравнения (8.2) определяются как абсциссы точек пересечения графиков функций f 1 ( x ) и f 2 ( x ).

Замечание. Известно, что все корни алгебраического уравнения

f(z) = a 0 z n + a 1 z n-1 +…+ a n-1 z + a n = 0

расположены в кольце

» xml:lang=»ru-RU» lang=»ru-RU»>Метод деления отрезка пополам

Простейшим алгоритмом уточнения корня на отрезке [ a , b ], если f ( x ) непрерывная функция и f ( a ) f ( b ) метод деления отрезка пополам . Очевидно, что середина отрезка служит приближением к корню уравнения (8.1) с точностью

ε ═ ( b — a )/2. В средней точке отрезка [ a , b ] определяется знак функции f ( x ), затем выбирается та половина отрезка, на концах которой функция принимает значения разных знаков, и деление повторяется. Если требуется найти корень с точностью до ε , то деление отрезка пополам продолжается до тех пор, пока длина отрезка не станет меньше ε/2 . Тогда середина последнего даст значение корня с требуемой точностью.

» xml:lang=»ru-RU» lang=»ru-RU»> 8.3 Метод простой итерации

Он состоит в том, что уравнение (8.1) заменяется эквивалентным уравнением вида

и итерации образуются по правилу

x n +1 = s ( x n ), n = 0,1,…,

причём задаётся начальное приближение x 0 . Для сходимости большое значение имеет выбор функции s ( x ).

Метод простой итерации сходится при надлежащем выборе начального приближения х 0 , если

в некоторой окрестности корня. Более точно:

Теорема. Если | s ‘ ( x )|  q  [ a — r , a + r ] , причём | s ( a ) a |  (1- q ) r , то уравнение (8.2) имеет единственное решение х  и метод простой итерации сходится к х  при любом начальном приближении х 0  [ a — r , a + r ].

Для метода простой итерации можно пользоваться следующей оценкой погрешности

| x k x  |  ――― | s ( x 0 ) x 0 |, k = 1,2,….

Где х  — истинное значение корня, | s  ( x )|  q для х  [ a , b ], х 0  [ a , b ]. Если функцию s ( x ) в уравнении (8.3) берём в виде

s ( x ) = x +  f ( x ),  = const ,

то получаем так называемый метод релаксации . Параметр  выбирается таким образом, чтобы выполнялась оценка (8.4). Если в некоторой окрестности корня выполняются условия

f  ( x ) m 1 f  ( x )| M 1 ,

то метод релаксации сходится при  (0, 2/М 1 ) . Наиболее быстрая скорость сходимости достигается пр оптимальном значении параметра  0 = 2/(М 1 +м 1 ). При этом значении для погрешности справедлива оценка

| x n — x  |   0 n | x 0 — x  |,

Пример. Решим уравнение

f ( x ) = x 3 +3 x 2 1 =0

методом простой итерации с точностью  = 0.5*10 -4 .

По графику находим, что уравнение имеет три корня, расположенных на отрезках [-3;-2] , [-1;0] и [0;1]. Найдём корень на отрезке [-3;-2]. Поделим уравнение на х 2 и приведём к виду

Положим s ( x ) = 1/ x 2 3 и возьмём х 0 = -2.5. На отрезке [-3;-2] ( r = 0.5) выполняются условия теоремы:

max | s  ( x ) | = q = ¼, | s ( x 0 ) x 0 | = 0.34  (1- q ) r = 0.375.

Найдём число итераций, необходимых для достижения заданной точности:

После шести итераций получаем приближенное значение корня 2.87938.

На отрезках [-1;0] и [0;1] представление (8.5) не годится для нахождения корней, поскольку производная функции s ( x ) больше 1 на этих отрезках. Для нахождения корней здесь удобно использовать представления

» xml:lang=»ru-RU» lang=»ru-RU»>Метод Ньютона и метод секущих

Метод Ньютона в случае простого вещественного корня имеет вид

x k +1 = x k — ――― , k = 1,2,…. (8.6)

в случае корня кратности 

f ′( x k )―――― + f ( x k ) = 0 .

Оценка погрешности следующая:

| х k — x  |  q | x 0 — x  |, k = 1,2,….

Можно пользоваться оценкой погрешности как в методе простой итерации, учитывая, что метод Ньютона

Видео:Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Модифицированный метод Ньютона

x k +1 = x k — ――― , k = 0, 1, ….

применяют в том случае, когда хотят избежать многократного вычисления производной  ( x k ).

В методе Ньютона требуется вычислять производную функции, что не всегда удобно. Можно заменить производную первой разделённой разностью, найденной по двум последним итерациям. Тогда вместо метода Ньютона (8.6) получим метод секущих

( x k x k -1 ) f ( x k )

f ( x k ) f ( x k -1 )

Для начала процесса требуется знать значения х 0 и х 1 .

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ.

1.Отделить вещественные корни аналитически или графически.

2.Уточнить корни делением отрезка пополам (если это возможно) с точностью до 0.1.

3.Уточнить корни заданным методом с заданной точностью.

Для метода Ньютона и метода простой итерации число итераций, необходимое для достижения заданной точности, выбрать заранее, сделав вручную оценку погрешности. Для остальных методов итерации прекращаются после того, как разность двух последовательных приближений становится меньше заданной точности.

4.Проверить результаты подстановкой найденных значений в уравнение.

1. Найти все корни уравнения

1000000 x 4 — 3000 x 3 + 1000002 x 2 — 3000 х + 2 = 0

с точностью 0.0001 методом а) Ньютона б) секущих.

2. Найти все корни уравнения

x 4 — 10001.01 x 3 -9800.01 x 2 — 999901 х + 10000 = 0

с точностью 0.001 а) методом Ньютона б) Модифицированным методом Ньютона.

3. Найти все корни уравнения

на отрезке [0.1 ; 0.5] с точностью 0.001 методом Ньютона.

4. Найти все корни уравнения

методом простой итерации с точностью до 0.001 сделав предварительную оценку погрешности.

5. Найти корень уравнения

x 4 — 20 x 3 + 101 x 2 — 20 х + 1 = 0

на отрезке [-1,1] с точностью 0.0001 методом Ньютона с параметрами

р=1 и р=2. Сравнить количества итераций необходимые для достижения

6. Найти корень уравнения

с точностью 0.0001 методом Ньютона и модифицированным методом Ньютона. Итерации производить пока разность между соседними итерациями не станет меньше заданной точности. Сравнить необходимые количества итераций.

7. Найти все корни уравнения

x 5 — 3 x 2 + 1 = 0

методом парабол с точностью 0.0005.

8. Найти вещественные корни уравнения

методом парабол с точностью 0.001.

9. Выяснить, к какому из корней 0, 1,-1 уравнения

сходится метод Ньютона, если начинать с произвольного начального приближения. Какие начальные приближения дают расходимость метода?

10. Найти все корни уравнения

x 3 + 3 x 2 — 1 = 0

методом простой итерации с точностью 0. 0005.

11. Найти все корни уравнения

х 4 — 10000.01 x 3 +101 x 2 — 10000.01 х + 100 = 0

с точностью до 0.001 а) методом Ньютона б) модифицированным методом Ньютона.

12. Найти корень уравнения

arccos ( x /2) = x 2

на отрезке [0,2] а) методом Ньютона б) модифицированным методом Ньютона.

13. Найти все корни уравнения

x 4 0.015х 3 + 0.3х 2 + х 1 = 0

с точностью 0.00001 методом а) Ньютона б) секущих.

14. Найти корень уравнения

х 3 sin (2 x ) = 1

методом парабол с точностью 0.001.

15. Найти все корни уравнения

х 3 1777х 2 + 777 = 0

на отрезке [-1,1] методом парабол с точностью до 0.0001

16. Найти все корни уравнения

5555х 4 555х 3 55х 2 5х = 0

с точностью 0.00001 методом а) Ньютона б) секущих.

17. Найти корень уравнения

на отрезке [-1,1] а) методом Ньютона б) модифицированным методом Ньютона.

18 . Найти корень уравнения

sin ( x 4 ) = 1 2 x

методом парабол с точностью 0.0001.

19 . Найти корень уравнения

с точностью 0.001 методом Ньютона. Итерации производить пока разность между соседними итерациями не станет меньше заданной точности. Сравнить необходимые количества итераций.

20. Найти все корни уравнения

x 3 45 x 2 + 43 = 0

на отрезке [-2,1] а) модифицированным методом Ньютона б) методом секущих.

21 . Найти корень уравнения

arcsin ( x ) + e x = 2

методом простой итерации с точностью до 0.001 сделав предварительную оценку погрешности.

22. Найти все корни уравнения

54 x 4 + x 2 0.0000001 =0

с точностью 0.00001 методом а) Ньютона б) секущих.

23. Найти все корни уравнения

tg ( x /3) x 3 = 0

методом парабол с точностью 0.001.

24. Найти все корни уравнения

12 x 4 + 11 x 3 10 x 2 999 = 0

на отрезке [-3.5,3] с точностью 0.0001 методом Ньютона с параметрами

р=1 и р=2. Сравнить количества итераций необходимые для достижения

25 . Найти корень уравнения

ОТВЕТЫ:1) 0,0100; 0,0200 2) 0,688; 10000 3) 0,107; 0,155; 0,361 4) 1,32; 0; 1,32 5) 0,0917; 0,1125 6) 0 7) 0,5611; 0,5992; 1,348 8) 0,637; 1,41 9) 1; 0; 1 10) -2,879; -0,6527; 0,5321 11) 0,231; 10000 12) 1,01817183 13) 1,1468; 0,66935; 1 14) 1,191 15) -0,6611; 0,6614 16) 0,09811;0,19695 17) 0,028959 18) 0,4746 19) 0,987 20) 0,9672; 0,9884; 44,98 21) 0,4369 22) +/- 0,0003 23) +/- 0,581; 0 24) -3,36; 2,875 25) 1,2784.

Узнать стоимость написания работы —>