Определенный интеграл это числовой интервал уравнение совокупность функций число функция

Первообразная

Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого .

Операция нахождения первообразной функции f(x), называется интегрированием.

Неопределенный интеграл

Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:

,

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.

Дифференциал-произвольное, бесконечно малое приращение переменной величины.

Свойства неопределённого интеграла

Таблица основных неопределённых интегралов

В виде

,

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.

Определённый интеграл

Определенный интеграл— Приращение одной из первообразных функции f(x) на отрезке [a;b].

Общий вид определённого интеграла:

где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал

Свойства определённого интеграла: см. св-ва определённого интеграла.

Определённый интеграл вычисляется по формуле Ньютона –Лейбница:

Применение определённого интеграла:

1. Нахождение площади криволинейной трапеции

2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е

Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.

Решение:

3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.

Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.

Решение:

Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.

Видео:Определенный интеграл. 11 класс.Скачать

Определение и условия существования определенного интеграла

Видео:Математика без Ху!ни. Определенные интегралы, часть 1.Скачать

Задачи, приводящие к понятию определенного интеграла.

Площадь криволинейной трапеции.

Пусть функция (f) непрерывна на отрезке (Delta = [a, b]) и неотрицательна, то есть (f(x) geq 0) при всех (x in Delta). Рассмотрим фигуру (G) (рис. 34.1), ограниченную отрезками прямых (x = a, x = b, y = 0) и графиком функции (y = f(x)), то есть
$$
G = .nonumber
$$

Такую фигуру называют криволинейной трапецией, а отрезок (Delta) — ее основанием.

Рис. 34.1

Разобьем отрезок (Delta) на (n) частей точками (x_(i = overline)), где (x_ Пример 1.

Найти площадь фигуры, ограниченной параболой (y = x^) и отрезками прямых (x = a), где (a > 0), и (y = 0) (рис. 34.2).

(triangle) Пользуясь тем, что предел суммы (sigma) для непрерывной функции (f(x) = x^) (см. раздел «Классы интегрируемых функций») не зависит от способа дробления отрезка (Delta = [0, a]) и выбора точек (xi_) будем считать, что отрезок (Delta) разбит на (n) отрезков равной длины, а в качестве точки (xi_ (i = overline)) взят правый конец отрезка (Delta_). Тогда (xi_ = x_ = displaystyle fraci, Delta x_ = frac, sigma = sum_ <substack>^<substack>x_^Delta x_ = frac<a^><n^>sum_ <substack>^<substack>i^).

Так как (displaystyle sum_^i^ = frac) (доказательство представлено здесь), то (sigma =displaystyle frac<a^>left(1 + fracright)left(1 + fracright)), откуда (displaystyle lim_ sigma = frac<a^>). Поэтому искомая площадь равна (displaystyle frac<a^>). (blacktriangle)

Заметим, что этот результат был получен еще Архимедом с помощью предельного перехода. Существует также простой способ нахождения предела для (sigma), основанный на формуле Ньютона Лейбница.

Работа переменной силы.

Пусть материальная точка движется вдоль числовой прямой (Ox) под действием силы (P), причем направление действия силы совпадает с направлением движения материальной точки. Предположим, что сила (P) задана как непрерывная функция от координаты (x) этой прямой, то есть (P = P(x)).

Найдем работу силы (P) при перемещении материальной точки от (x = a) до (x = b). Разобьем отрезок [(a, b)], как и в задаче о площади криволинейной трапеции, точками (x_) и выберем (xi_ in Delta_ (i = overline)). Тогда работа силы (P) на отрезке (Delta_) приближенно равна (P(xi_)Delta x_), а на отрезке [(a, b)] работу этой силы можно считать приближенно равной сумме (displaystyle sum_^P(xi_)Delta x_). Предел этой суммы (при тех же условиях, что и в задаче о площади) естественно назвать работой переменной силы при перемещении материальной точки из точки (a) в точку (b).

В рассмотренных задачах речь идет о нахождении предела сумм вида (displaystyle sum_^f(xi_)Delta x_), которые называют интегральными суммами. К вычислению предела таких сумм сводится решение многих важных задач из геометрии, физики, техники и других дисциплин. Поэтому вопросы, связанные с обоснованием предельного перехода описанного типа, заслуживают всестороннего изучения.

Видео:ИНТЕГРАЛ С НУЛЯ | определенный интеграл | ТАБЛИЦА ИНТЕГРАЛОВ | сумма РиманаСкачать

Понятие определенного интеграла.

Пусть функция одного переменного (f(x)) определена на отрезке [(a, b)] и пусть (x_ (i = overline)) — совокупность точек этого отрезка таких, что
$$
a = x_ Определение.

Если существует число (J), определяемое условиями eqref, то функцию (f) называют интегрируемой (по Риману) на отрезке ([a, b]) и говорят, что существует интеграл от функции (f) на отрезке ([a, b]).

Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

math4school.ru

Видео:Неопределенный интеграл. 11 класс.Скачать

Первообразная и интегралы

Первообразная

Функция F(x ) называется первообразной для функции f(x) на заданном промежутке, если для всех x из этого промежутка выполняется равенство

► Например, функция F(x) = х 2 является первообразной для функции f(x ) = 2х , так как

Основное свойство первообразной

Если F(x) — первообразная для функции f(x) на заданном промежутке, то функция f(x) имеет бесконечно много первообразных, и все эти первообразные можно записать в виде F(x) + С, где С — произвольная постоянная.

Правила вычисления первообразных

1. Если F(x) — первообразная для f(x) , а G(x) — первообразная для g(x) , то F(x) + G(x) — первообразная для f(x) + g(x) . Иными словами, первообразная суммы равна сумме первообразных .
2. Если F(x) — первообразная для f(x) , и k — постоянная, то k· F(x) — первообразная для k· f(x) . Иными словами, постоянный множитель можно выносить за знак производной .
3. Если F(x) — первообразная для f(x) , и k , b — постоянные, причём k ≠ 0 , то 1 / k· F( k x + b ) — первообразная для f (kx + b ) .

Неопределённый интеграл

Неопределённым интегралом от функции f(x) называется выражение F(x) + С, то есть совокупность всех первообразных данной функции f(x) . Обозначается неопределённый интеграл так:

f(x) — называют подынтегральной функцией ;

f(x) dx — называют подынтегральным выражением ;

x — называют переменной интегрирования ;

F(x) — одна из первообразных функции f(x) ;

С — произвольная постоянная.

Слово «интеграл» происходит от латинского слова integer , что означает «восстановленный». Считая неопределённый интеграл от 2 x , мы как бы восстанавливаем функцию х 2 , производная которой равна 2 x . Восстановление функции по её производной, или, что то же, отыскание неопределённого интеграла по данной подынтегральной функции, называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию.Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

Основные свойства неопределённого интеграла

Производная неопределённого интеграла равна подынтегральной функции:

Постоянный множитель подынтегрального выражения можно выносить за знак интеграла:

Интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций:

Если k , b — постоянные, причём k ≠ 0 , то

Таблица первообразных и неопределённых интегралов

(nneq-1)$$$$frac<x^>+C$$$$int x^ndx=frac<x^>+C$$IV.$$frac$$$$ln |x|+C$$$$intfrac=ln |x|+C$$V.$$sin x$$$$-cos x+C$$$$intsin x

dx=-cos x+C$$VI.$$cos x$$$$sin x+C$$$$intcos x

dx=sin x+C$$VII.$$frac$$$$textrm

x+C$$$$intfrac=textrm

x+C$$VIII.$$frac$$$$-textrm

x+C$$$$intfrac=-textrm

x+C$$IX.$$e^x$$$$e^x+C$$$$int e^xdx=e^x+C$$X.$$a^x$$$$frac+C$$$$int a^xdx=frac+C$$XI.$$frac<sqrt>$$$$arcsin x +C$$$$intfrac<sqrt>=arcsin x +C$$XII.$$frac<sqrt>$$$$arcsin frac+C$$$$intfrac<sqrt>=arcsin frac+C$$XIII.$$frac$$$$textrm

x+C$$$$int frac=textrm

x+C$$XIV.$$frac$$$$fractextrm

(aneq0)$$$$fracln beginfracend+C$$$$intfrac=fracln beginfracend+C$$XVII.$$textrm

x$$$$-ln |cos x|+C$$$$int textrm

dx=-ln |cos x|+C$$XVIII.$$textrm

x$$$$ln |sin x|+C$$$$int textrm

dx=ln |sin x|+C$$XIX.$$ frac $$$$ln begintextrm

fracend+C $$$$int frac=ln begintextrm

fracend+C $$XX.$$ frac $$$$ln begintextrmleft (frac+frac right ) end+C $$$$int frac=ln begintextrmleft (frac+frac right ) end+C $$Первообразные и неопределённые интегралы, приведённые в этой таблице, принято называть табличными первообразными и табличными интегралами .

Определённый интеграл

Пусть на промежутке [a; b] задана непрерывная функция y = f(x) , тогда определённым интегралом от a до b функции f(x) называется приращение первообразной F(x) этой функции, то есть

Числа a и b называются соответственно нижним и верхним пределами интегрирования.

Основные правила вычисления определённого интеграла

Замечание . Во всех случаях предполагается, что подынтегральные функции интегрируемые на числовых промежутках, границами которых являются пределы интегрирования.

Геометрический и физический смысл определённого интеграла

Площадь фигуры

Геометрический смысл определённого интеграла	Физический смысл определённого интеграла

Если на заданном промежутке [a; b] определены и непрерывны функции y = f(x) и y = g(x) , которые удовлетворяют условию

► Например. Вычислим площадь фигуры, ограниченной линиями

Объём тела вращения

Если тело вращения получено в результате вращения фигуры, ограниченной сверху и снизу графиками функций y = f(x) и y = g(x) , соответственно, то

► Например. Вычислим объём конуса с радиусом r и высотой h . Расположим конус в прямоугольной системе координат так, чтобы его ось совпадала с осью Ox , а центр основания располагался в начале координат. Вращение образующей AB определяет конус. Так как уравнение AB 💡 Видео Определенные и неопределенные интегралы для чайников. Свойства интегралов.Скачать 11 класс, 20 урок, Первообразная и неопределённый интегралСкачать Примеры решения определенных интеграловСкачать Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать Как найти предел с помощью интеграла?Скачать 11 класс, 21 урок, Определённый интегралСкачать Первообразная. 11 класс.Скачать Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать Свойства определенного интеграла ЧАСТЬ1Скачать Определенный интеграл с переменным верхним пределом и его производная по верхнему пределуСкачать Определенный интеграл и применение интеграловСкачать ✓ Формула Ньютона-Лейбница. Что такое первообразная и интеграл | Осторожно, спойлер! | Борис ТрушинСкачать 9 класс, 2 урок, Множества и операции над нимиСкачать Определённый интеграл. ПлощадьСкачать 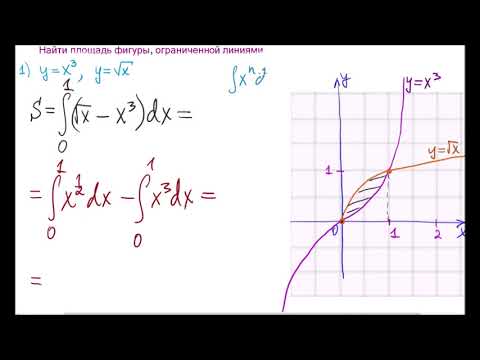Интеграл: Азы интегрирования. Высшая математикаСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства