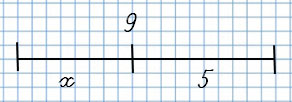Буквенное выражение (или выражение с переменными) — это математическое выражение, которое состоит из чисел, букв и знаков математических операций. Например, следующее выражение является буквенным:
С помощью буквенных выражений можно записывать законы, формулы, уравнения и функции. Умение манипулировать буквенными выражениями — залог хорошего знания алгебры и высшей математики.
Любая серьёзная задача в математике свóдится к решению уравнений. А чтобы уметь решать уравнения, нужно уметь работать с буквенными выражениями.
Чтобы работать с буквенными выражениями, нужно хорошо изучить базовую арифметику: сложение, вычитание, умножение, деление, основные законы математики, дроби, действия с дробями, пропорции. И не просто изучить, а понять досконально.
- Переменные
- Коэффициенты
- Как определить коэффициент
- Слагаемые в буквенных выражениях
- Подобные слагаемые
- Упрощение выражений
- Тождества. Тождественно равные выражения
- Выражения и уравнения — определение и вычисление с примерами решения
- Выражения и уравнения
- Правила раскрытия скобок
- Уравнения. Основные свойства уравнений
- Основные свойства уравнений
- Применение уравнений к решению задач
- Перпендикулярные и параллельные прямые
- Перпендикулярные прямые
- Параллельные прямые
- Координатная плоскость
- Графики зависимостей между величинами
- Уравнения
- Уравнение
- Схемы уравнения
- Решение уравнений
- х + 5 = 9
- 5 + х = 9
- 9 — х = 5
- х — 4 = 5
- 🎬 Видео
Видео:АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 7 класс ПРИМЕРЫ формулы КАК РЕШАТЬ урок 1Скачать

Переменные
Буквы, которые содержатся в буквенных выражениях, называются переменными.
Например, в выражении a + b + 4 переменными являются буквы a и b. Если вместо этих переменных подставить любые числа, то буквенное выражение a + b + 4 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных a и b. Для изменения значений используется знак равенства
Мы изменили значения переменных a и b. Переменной a присвоили значение 2 , переменной b присвоили значение 3. В результате буквенное выражение a + b + 4 обращается в обычное числовое выражение 2 + 3 + 4, значение которого можно найти:
Когда происходит умножение переменных, то они записываются вместе. Например, запись ab означает то же самое, что и запись a × b . Если подставить вместо переменных a и b числа 2 и 3 , то мы получим 6
Слитно также можно записать умножение числа на выражение в скобках. Например, вместо a × (b + c) можно записать a(b + c) . Применив распределительный закон умножения, получим a(b + c) = ab + ac .
Видео:Алгебраические выражения. 6 класс.Скачать

Коэффициенты
В буквенных выражениях часто можно встретить запись, в которой число и переменная записаны вместе, например 3a . На самом деле это короткая запись умножения числа 3 на переменную a и эта запись выглядит как 3 × a .
Другими словами, выражение 3a является произведением числа 3 и переменной a. Число 3 в этом произведении называют коэффициентом. Этот коэффициент показывает во сколько раз будет увеличена переменная a . Данное выражение можно прочитать как «a три раза» или «трижды а«, или «увеличить значение переменной a в три раза», но наиболее часто читается как «три a«
К примеру, если переменная a равна 5 , то значение выражения 3a будет равно 15 .
Говоря простым языком, коэффициент это число, которое стоит перед буквой (перед переменной).
Букв может быть несколько, например 5abc . Здесь коэффициентом является число 5 . Данный коэффициент показывает, что произведение переменных abc увеличивается в пять раз. Это выражение можно прочитать как « abc пять раз» либо «увеличить значение выражения abc в пять раз», либо «пять abc «.
Если вместо переменных abc подставить числа 2, 3 и 4, то значение выражения 5abc будет равно 120
5 × 2 × 3 × 4 = 120
Можно мысленно представить, как сначала перемнóжились числа 2, 3 и 4, и полученное значение увеличилось в пять раз:
Знак коэффициента отнóсится только к коэффициенту, и не отнóсится к переменным!
Рассмотрим выражение −6b . Минус, стоящий перед коэффициентом 6 , отнóсится только к коэффициенту 6 , и не отнóсится к переменной b . Понимание этого факта позвóлит не ошибаться в будущем со знаками.
Найдем значение выражения −6b при b = 3 .
−6b это короткая форма записи от −6 × b . Для наглядности запишем выражение −6b в развёрнутом виде и подставим значение переменной b
Пример 2. Найти значение выражения −6b при b = −5
Запишем выражение −6b в развёрнутом виде
и далее подставим значение переменной b
Пример 3. Найти значение выражения −5a + b при a = 3 и b = 2
−5a + b это короткая форма записи от −5 × a + b , поэтому для наглядности запишем выражение −5 × a + b в развёрнутом виде и подстáвим значения переменных a и b
−5a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13
Иногда буквы записаны без коэффициента, например a или ab . В этом случае коэффициентом является единица:
но единицу по традиции не записывают, поэтому просто пишут a или ab
Если перед буквой стоит минус, то коэффициентом является число −1 . Например, выражение −a на самом деле выглядит как −1a . Это произведение минус единицы и переменной a. Оно получилось следующим образом:
Здесь крóется небольшой подвох. В выражении −a минус, стоящий перед переменной a на самом деле относится к невидимой единице, а не к переменной a . Поэтому при решении задач следует быть внимательным.
К примеру, если дано выражение −a и нас прóсят найти его значение при a = 2 , то в школе мы подставляли двойку вместо переменной a и получали ответ −2 , не особо зацикливаясь на том, как это получалось. На самом деле происходило умножение минус единицы на положительное число 2
Если дано выражение −a и требуется найти его значение при a = −2 , то мы подставляем −2 вместо переменной a
Чтобы не допускать ошибок, первое время невидимые единицы можно записывать явно.
Пример 4. Найти значение выражения abc при a=2 , b=3 и c=4
Выражение abc это короткая форма записи от 1×a×b×c. Для наглядности запишем выражение abc в развёрнутом виде и подставим значения переменных a , b и c
1 × a × b × c = 1 × 2 × 3 × 4 = 24
Пример 5. Найти значение выражения abc при a=−2 , b=−3 и c=−4
Запишем выражение abc в развёрнутом виде и подставим значения переменных a , b и c
1 × a × b × c = 1 × (−2) × (−3) × (−4) = −24
Пример 6. Найти значение выражения −abc при a=3 , b=5 и c=7
Выражение −abc это короткая форма записи от −1×a×b×c. Для наглядности запишем выражение −abc в развёрнутом виде и подставим значения переменных a , b и c
−abc = −1 × a × b × c = −1 × 3 × 5 × 7 = −105
Пример 7. Найти значение выражения −abc при a=−2 , b=−4 и c=−3
Запишем выражение −abc в развёрнутом виде:
−abc = −1 × a × b × c
Подставим значение переменных a , b и c
−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24
Видео:Числовые выражения. Буквенные выражения. 1 часть. 5 класс.Скачать

Как определить коэффициент
Иногда требуется решить задачу, в которой требуется определить коэффициент выражения. В принципе, данная задача очень простá. Достаточно уметь правильно умножать числа.
Чтобы определить коэффициент в выражении, нужно отдельно перемножить числа, входящие в это выражение, и отдельно перемножить буквы. Получившийся числовой сомножитель и будет коэффициентом.
Пример 1. Определить коэффициент в выражении: 7m×5a×(−3)×n
Выражение состоит из нескольких сомножителей. Это можно отчетливо увидеть, если записать выражение в развёрнутом виде. То есть произведения 7m и 5a записать в виде 7×m и 5×a
7 × m × 5 × a × (−3) × n
Применим сочетательный закон умножения, который позволяет перемножать сомножители в любом порядке. А именно, отдельно перемнóжим числа и отдельно перемнóжим буквы (переменные):
−3 × 7 × 5 × m × a × n = −105man
Коэффициент равен −105. После завершения буквенную часть желательно расположить в алфавитном порядке:
Пример 2. Определить коэффициент в выражении: −a×(−3)×2
Перемножим отдельно числа и буквы:
−a × (−3 ) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a
Коэффициент равен 6.
Пример 3. Определить коэффициент в выражении:
Перемножим отдельно числа и буквы:
Коэффициент равен −1. Обратите внимание, что единица не записана, поскольку коэффициент 1 принято не записывать.
Эти казалось бы простейшие задачи могут сыграть с нами очень злую шутку. Часто выясняется, что знак коэффициента поставлен не верно: либо пропущен минус либо наоборот он поставлен зря. Чтобы избежать этих досадных ошибок, тема умножения целых чисел должна быть изучена на хорошем уровне.
Видео:АЛГЕБРА 7 класс : Выражения с переменнымиСкачать

Слагаемые в буквенных выражениях
При сложении нескольких чисел получается сумма этих чисел. Числа, которые складывают называют слагаемыми. Слагаемых может быть несколько, например:
Когда выражение состоит из слагаемых, вычислять его намного проще, поскольку складывать легче, чем вычитать. Но в выражении может присутствовать не только сложение, но и вычитание, например:
В этом выражении числа 3 и 5 являются вычитаемыми, а не слагаемыми. Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
Не суть, что числа −3 и −5 теперь со знаком минус. Главное, что все числа в данном выражении соединены знаком сложения, то есть выражение является суммой.
Оба выражения 1 + 2 − 3 + 4 − 5 и 1 + 2 + (−3) + 4 + (−5) равны одному и тому значению — минус единице:
1 + 2 − 3 + 4 − 5 = −1
1 + 2 + (−3) + 4 + (−5) = −1
Таким образом, значение выражения не пострадает от того, что мы где-то заменим вычитание сложением.
Заменять вычитание сложением можно и в буквенных выражениях. Например, рассмотрим следующее выражение:
7a + 6b − 3c + 2d − 4s
Заменим вычитание сложением там, где это можно:
7a + 6b + (−3c) + 2d + (−4s)
При любых значениях переменных a, b, c, d и s выражения 7a + 6b − 3c + 2d − 4s и 7a + 6b + (−3c) + 2d + (−4s) будут равны одному и тому же значению.
Вы должны быть готовы к тому, что учитель в школе или преподаватель в институте может называть слагаемыми даже те числа (или переменные), которые ими не являются.
Например, если на доске будет записана разность a − b , то учитель не будет говорить, что a — это уменьшаемое, а b — вычитаемое. Обе переменные он назовет одним общим словом — слагаемые . А всё потому, что выражение вида a − b математик видит, как сумму a + (−b) . В таком случае выражение становится суммой, а переменные a и (−b) станóвятся слагаемыми.
Видео:МАТЕМАТИКА 5 класс: Числовые и буквенные выраженияСкачать

Подобные слагаемые
Подобные слагаемые — это слагаемые, которые имеют одинаковую буквенную часть.
Например, рассмотрим выражение 7a + 6b + 2a . Слагаемые 7a и 2a имеют одинаковую буквенную часть — переменную a. Значит слагаемые 7a и 2a являются подобными.
Обычно подобные слагаемые складывают, чтобы упростить выражение или решить какое-нибудь уравнение. Это действие называют приведéнием подобных слагаемых.
Чтобы привести подобные слагаемые, нужно сложить коэффициенты этих слагаемых, и полученный результат умножить на общую буквенную часть.
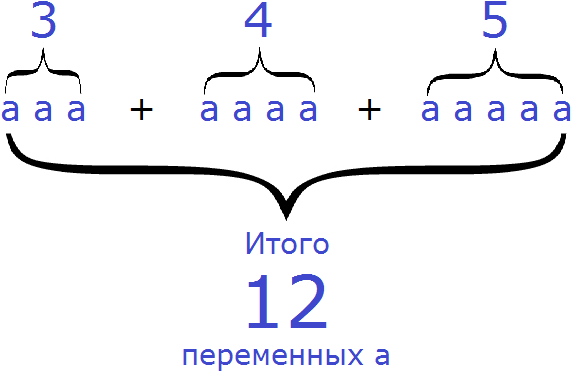
Например, приведём подобные слагаемые в выражении 3a + 4a + 5a . В данном случае подобными являются все слагаемые. Слóжим их коэффициенты и результат умножим на общую буквенную часть — на переменную a
3a + 4a + 5a = (3 + 4 + 5)×a = 12a
Подобные слагаемые обычно привóдят в уме и результат записывают сразу:
3a + 4a + 5a = 12a
Также, можно рассуждать следующим образом:
Было 3 переменные a , к ним прибавили еще 4 переменные a и ещё 5 переменных a. В итоге получили 12 переменных a
Если подсчитать на рисунке количество переменных a, то насчитается 12.
Рассмотрим несколько примеров на приведение подобных слагаемых. Учитывая, что данная тема очень важна, на первых порах будем записывать подробно каждую мелочь. Несмотря на то, что здесь всё очень просто, большинство людей допускают множество ошибок. В основном по невнимательности, а не по незнанию.
Пример 1. Привести подобные слагаемые в выражении 3a + 2a + 6a + 8a
Сложим коэффициенты в данном выражении и полученный результат умножим на общую буквенную часть:
Конструкцию (3 + 2 + 6 + 8) × a можно не записывать, поэтому сразу запишем ответ
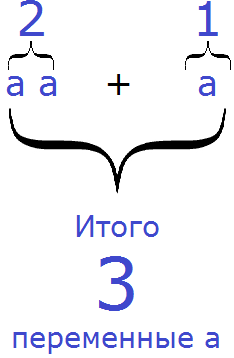
Пример 2. Привести подобные слагаемые в выражении 2a + a
Второе слагаемое a записано без коэффициента, но на самом деле перед ним стоит коэффициент 1, который мы не видим по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
Теперь приведем подобные слагаемые. То есть сложим коэффициенты и результат умножим на общую буквенную часть:
2a + 1a = (2 + 1) × a = 3a
Запишем решение покороче:
Приводя подобные слагаемые в выражении 2a+a, можно рассуждать и по-другому:
Было 2 переменные a , добавили ещё одну переменную a , в итоге получилось 3 переменные a .
Пример 3. Привести подобные слагаемые в выражении 2a − a
Заменим вычитание сложением:
Второе слагаемое (−a) записано без коэффициента, но на самом деле оно выглядит как (−1a). Коэффициент −1 опять же невидимый по причине того, что его не записывают. Стало быть, выражение выглядит следующим образом:
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть:
2a + (−1a) = (2 + (−1)) × a = 1a = a
Обычно записывают короче:
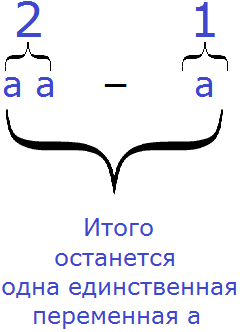
Приводя подобные слагаемые в выражении 2a−a можно рассуждать и по-другому:
Было 2 переменные a , вычли одну переменную a , в итоге осталась одна единственная переменная a
Пример 4. Привести подобные слагаемые в выражении 6a − 3a + 4a − 8a
Заменим вычитание сложение там, где это можно:
6a − 3a + 4a − 8a = 6a + (−3a) + 4a + (−8a)
Теперь приведем подобные слагаемые. Сложим коэффициенты и результат умножим на общую буквенную часть
(6 + (−3) + 4 + (−8)) × a = −1a = −a
Запишем решение покороче:
6a − 3a + 4a − 8a = −a
Встречаются выражения, которые содержат несколько различных групп подобных слагаемых. Например, 3a + 3b + 7a + 2b . Для таких выражений справедливы те же правила, что и для остальных, а именно складывание коэффициентов и умножение полученного результата на общую буквенную часть. Но чтобы не допустить ошибок, удобно разные группы слагаемых подчеркнуть разными линиями.
Например, в выражении 3a + 3b + 7a + 2b те слагаемые, которые содержат переменную a, можно подчеркнуть одной линией, а те слагаемые которые содержат переменную b, можно подчеркнуть двумя линиями:
Теперь можно привести подобные слагаемые. То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть. Сделать это нужно для обеих групп слагаемых: для слагаемых, содержащих переменную a и для слагаемых содержащих переменную b.
3a + 3b + 7a + 2b = (3+7)×a + (3 + 2)×b = 10a + 5b
Опять же повторимся, выражение несложное, и подобные слагаемые можно приводить в уме:
3a + 3b + 7a + 2b = 10a + 5b
Пример 5. Привести подобные слагаемые в выражении 5a − 6a −7b + b
Заменим вычитание сложение там, где это можно:
5a − 6a −7b + b = 5a + (−6a) + (−7b) + b
Подчеркнём подобные слагаемые разными линиями. Слагаемые, содержащие переменные a подчеркнем одной линией, а слагаемые содержащие переменные b , подчеркнем двумя линиями:
Теперь можно привести подобные слагаемые. То есть сложить коэффициенты и полученный результат умножить на общую буквенную часть:
5a + (−6a) + (−7b) + b = (5 + (−6))×a + ((−7) + 1)×b = −a + (−6b)
Если в выражении содержатся обычные числа без буквенных сомножителей, то они складываются отдельно.
Пример 6. Привести подобные слагаемые в выражении 4a + 3a − 5 + 2b + 7
Заменим вычитание сложением там, где это можно:
4a + 3a − 5 + 2b + 7 = 4a + 3a + (−5) + 2b + 7
Приведем подобные слагаемые. Числа −5 и 7 не имеют буквенных сомножителей, но они являются подобными слагаемыми — их необходимо просто сложить. А слагаемое 2b останется без изменений, поскольку оно единственное в данном выражении, имеющее буквенный сомножитель b, и его не с чем складывать:
4a + 3a + (−5) + 2b + 7 = (4 + 3)×a + 2b + (−5) + 7 = 7a + 2b + 2
Запишем решение покороче:
4a + 3a − 5 + 2b + 7 = 7a + 2b + 2
Слагаемые можно упорядочивать, чтобы те слагаемые, которые имеют одинаковую буквенную часть, располагались в одной части выражения.
Пример 7. Привести подобные слагаемые в выражении 5t+2x+3x+5t+x
Поскольку выражение является суммой из нескольких слагаемых, это позволяет нам вычислять его в любом порядке. Поэтому слагаемые, содержащие переменную t , можно записать в начале выражения, а слагаемые содержащие переменную x в конце выражения:
5t + 5t + 2x + 3x + x
Теперь можно привести подобные слагаемые:
5t + 5t + 2x + 3x + x = (5+5)×t + (2+3+1)×x = 10t + 6x
Запишем решение покороче:
5t + 2x + 3x + 5t + x = 10t + 6x
Сумма противоположных чисел равна нулю. Это правило работает и для буквенных выражений. Если в выражении встретятся одинаковые слагаемые, но с противоположными знаками, то от них можно избавиться на этапе приведения подобных слагаемых. Иными словами, просто вычеркнуть их из выражения, поскольку их сумма равна нулю.
Пример 8. Привести подобные слагаемые в выражении 3t − 4t − 3t + 2t
Заменим вычитание сложением там, где это можно:
3t − 4t − 3t + 2t = 3t + (−4t) + (−3t) + 2t
Слагаемые 3t и (−3t) являются противоположными. Сумма противоположных слагаемых равна нулю. Если убрать этот ноль из выражения, то значение выражения не изменится, поэтому мы его и уберём. А уберём мы его обычным вычеркиванием слагаемых 3t и (−3t)
В итоге у нас останется выражение (−4t) + 2t. В данном выражении можно привести подобные слагаемые и получить окончательный ответ:
Запишем решение покороче:
Видео:Математика 2 класс (Урок№25 - Буквенные выражения.)Скачать

Упрощение выражений
Часто можно встретить задание, в котором сказано «упростите выражение» и далее приводится выражение, которое требуется упростить. Упростить выражение значит сделать его прóще и корóче.
На самом деле мы уже занимались упрощением выражений, когда сокращали дроби. После сокращения дробь становилась короче и проще для восприятия.
Рассмотрим следующий пример. Упростить выражение .
Это задание буквально можно понять так: «Примените к данному выражению любые допустимые действия, но сделайте его прóще» .
В данном случае можно осуществить сокращение дроби, а именно разделить числитель и знаменатель дроби на 2:
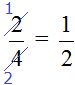

В итоге дробь упростилась до 0,5.
Первый вопрос, который нужно себе задавать при решении подобных задач, должен быть: «а что можно сделать?» . Потому что есть действия, которые можно делать, и есть действия, которые делать нельзя.
Ещё один важный момент, о котором нужно помнить, заключается в том что значение выражение не должно измениться после упрощения выражения. Вернемся к выражению . Данное выражение представляет собой деление, которое можно выполнить. Выполнив это деление, мы получаем значение данного выражения, которое равно 0,5
Но мы упростили выражение и получили новое упрощённое выражение 
Но выражение 
Таким образом, как бы мы не упрощали выражение, значение получаемых выражений по-прежнему равно 0,5. Значит упрощение выполнялось верно на каждом этапе. Именно к этому нужно стремиться при упрощении выражений — значение выражения не должно пострадать от наших действий.
Часто требуется упрощать буквенные выражения. Для них справедливы те же правила упрощения, что и для числовых выражений. Можно выполнять любые допустимые действия, лишь бы не изменилось значение выражения.
Рассмотрим несколько примеров.
Пример 1. Упростить выражение 5,21s × t × 2,5
Чтобы упростить данное выражение, можно отдельно перемножить числа и отдельно перемножить буквы. Это задание очень похоже на то, которое мы рассматривали, когда учились определять коэффициент:
5,21s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025st
Таким образом, выражение 5,21s × t × 2,5 упростилось до 13,025st .
Пример 2. Упростить выражение −0,4 × (−6,3b) × 2
Второе произведение (−6,3b) можно перевести в понятный для нас вид, а именно записать в виде ( −6,3)×b , затем отдельно перемножить числа и отдельно перемножить буквы:
Таким образом, выражение −0,4 × (−6,3b) × 2 упростилось до 5,04b
Пример 3. Упростить выражение
Распишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно перемножим буквы:
Таким образом, выражение 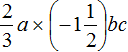
При упрощении выражений, дроби можно сокращать в процессе решения, а не в самом конце, как мы это делали с обычными дробями. Например, если в ходе решения мы наткнёмся на выражение вида , то вовсе необязательно вычислять числитель и знаменатель и делать что-то вроде этого:
Дробь можно сократить, выбирая по множителю в числителе и в знаменателе и сокращать эти множители на их наибольший общий делитель. Другими словами, использовать короткую версию сокращения дроби, в которой мы не расписываем подробно на что был разделен числитель и знаменатель.
Например, в числителе множитель 12 и в знаменателе множитель 4 можно сократить на 4. Четвёрку храним в уме, а разделив 12 и 4 на эту четвёрку, ответы записываем рядом с этими числами, предварительно зачеркнув их
Далее в числителе множитель 9 и в знаменателе множитель 3 можно сократить на 3
Далее в числителе множитель 6 и в знаменателе множитель 2 можно сократить на 2
Теперь можно перемножить получившиеся маленькие множители. В данном случае их немного и можно перемножить в уме:
Со временем можно обнаружить, что решая ту или иную задачу, выражения начинают «толстеть», поэтому желательно приучиться к быстрым вычислениям. То, что можно вычислить в уме, нужно вычислять в уме. То, что можно быстро сократить, нужно быстро сокращать.
Пример 4. Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение 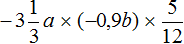
Пример 5. Упростить выражение
Перемножим отдельно числа и отдельно буквы:
Таким образом, выражение 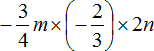
Пример 6. Упростить выражение
Запишем данное выражение более подробно, чтобы хорошо увидеть, где числа, а где буквы:
Теперь отдельно перемножим числа и отдельно буквы. Для удобства вычислений десятичную дробь −6,4 и смешанное число 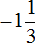
Таким образом, выражение 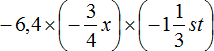
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Пример 7. Упростить выражение
Перемножим отдельно числа и отдельно буквы. Для удобства вычисления смешанное число 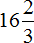
Таким образом, выражение 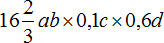
Обратите внимание на то, как сократилась дробь. Новые множители, которые получаются в результате сокращения предыдущих множителей, тоже допускается сокращать.
Теперь поговорим о том, чего делать нельзя. При упрощении выражений категорически нельзя перемножать числа и буквы, если выражение является суммой, а не произведением.
Например, если требуется упростить выражение 5a + 4b, то нельзя записывать следующим образом:
Это равносильно тому, что если бы нас попросили сложить два числа, а мы бы их перемножали вместо того, чтобы складывать.
При подстановке любых значений переменных a и b выражение 5a +4b обращается в обыкновенное числовое выражение. Предположим, что переменные a и b имеют следующие значения:
Тогда значение выражения будет равно 22
5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22
Сначала выполняется умножение, а затем полученные результаты складывают. А если бы мы попытались упростить данное выражение, перемножив числа и буквы, то получилось бы следующее:
5a + 4b = 5 × 4 × a × b = 20ab
20ab = 20 × 2 × 3 = 120
Получается совсем другое значение выражения. В первом случае получилось 22, во втором случае 120. Это означает, что упрощение выражения 5a + 4b было выполнено неверно.
После упрощения выражения, его значение не должно изменяться при одних и тех же значениях переменных. Если при подстановке в изначальное выражение любых значений переменных получается одно значение, то после упрощения выражения должно получаться то же самое значение, что и до упрощения.
С выражением 5a + 4b на самом деле ничего делать нельзя. Оно не упрощается.
Если в выражении содержатся подобные слагаемые, то их можно сложить, если нашей целью является упрощение выражения.
Пример 8. Упростить выражение 0,3a−0,4a+a
Чтобы упростить данное выражение можно привести подобные слагаемые:
0,3a − 0,4a + a = 0,3a + (−0,4a) + a = (0,3 + (−0,4) + 1)×a = 0,9a
или покороче: 0,3a − 0,4a + a = 0,9a
Таким образом, выражение 0,3a−0,4a+a упростилось до 0,9a
Пример 9. Упростить выражение −7,5a − 2,5b + 4a
Чтобы упростить данное выражение можно привести подобные слагаемые:
−7,5a − 2,5b + 4a = −7,5a + (−2,5b) + 4a = ((−7,5) + 4)×a + (−2,5b) = −3,5a + (−2,5b)
или покороче −7,5a − 2,5b + 4a = −3,5a + (−2,5b)
Слагаемое (−2,5b) осталось без изменений, поскольку его не с чем было складывать.
Пример 10. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Коэффициент 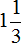
Таким образом, выражение 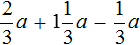
Пример 11. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение 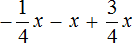
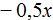
В данном примере целесообразнее было бы сложить первый и последний коэффициент в первую очередь. В этом случае мы получили бы короткое решение. Выглядело бы оно следующим образом:
Пример 12. Упростить выражение
Чтобы упростить данное выражение можно привести подобные слагаемые:
Таким образом, выражение 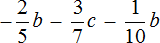
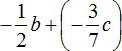
Слагаемое 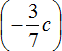
Данное решение можно записать значительно короче. Выглядеть оно будет следующим образом:
В коротком решении пропущены этапы замены вычитания сложением и подробная запись, как дроби приводились к общему знаменателю.
Ещё одно различие заключается в том, что в подробном решении ответ выглядит как 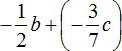
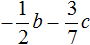
Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Тождества. Тождественно равные выражения
После того как мы упростили какое-нибудь выражение, оно станóвится проще и короче. Чтобы проверить верно ли упрощено выражение, достаточно подстáвить любые значения переменных сначала в предыдущее выражение, которое требовалось упростить, а затем в новое, которое упростили. Если значение в обоих выражениях будет одинаковым, то это означает, что выражение упрощено верно.
Рассмотрим простейший пример. Пусть требуется упростить выражение 2a × 7b . Чтобы упростить данное выражение, можно по-отдельности перемнóжить числа и буквы:
Проверим верно ли мы упростили выражение. Для этого подставим любые значения переменных a и b сначала в первое выражение, которое требовалось упростить, а затем во второе, которое упростили.
Пусть значения переменных a , b будут следующими:
Подстáвим их в первое выражение 2a × 7b
2a × 7b = 2 × 4 × 7 × 5 = 280
Теперь подстáвим те же значения переменных в выражение, которое получилось в результате упрощения выражения 2a × 7b , а именно в выражение 14ab
14ab = 14 × 4 × 5 = 280
Видим, что при a = 4 и b = 5 значение первого выражения 2a × 7b и значение второго выражения 14ab равны
2a × 7b = 2 × 4 × 7 × 5 = 280
14ab = 14 × 4 × 5 = 280
То же самое произойдет и для любых других значений. Например, пусть a = 1 и b = 2
2a × 7b = 2 × 1 × 7 × 2 = 28
14ab = 14 × 1 × 2 = 28
Таким образом, выражения 2a × 7b и 14ab при любых значениях переменных равны одному и тому же значению. Такие выражения называют тождественно равными.
Делаем вывод, что между выражениями 2a × 7b и 14ab можно поставить знак равенства, поскольку они равны одному и тому же значению:
Равенством называют любое выражение, которые соединено знаком равенства (=).
А равенство вида 2a × 7b = 14ab называют тождеством.
Тождеством называют равенство, которое верно при любых значениях переменных.
Другие примеры тождеств:
Да, законы математики, которые мы изучали, являются тождествами.
Верные числовые равенства тоже являются тождествами. Например:
Решая сложную задачу, чтобы облегчить себе вычисление, сложное выражение заменяют на более простое выражение, тождественно равное предыдущему. Такую замену называют тождественным преобразованием выражения или просто преобразованием выражения.
Например, мы упростили выражение 2a × 7b , и получили более простое выражение 14ab . Это упрощение можно называть тождественным преобразованием.
Часто можно встретить задание, в котором сказано «докажите, что равенство является тождеством» и далее приводится равенство, которое требуется доказать. Обычно это равенство состоит из двух частей: левой и правой части равенства. Наша задача состоит в том, чтобы выполнить тождественные преобразования с одной из частей равенства и получить другую часть. Либо выполнить тождественные преобразования с обеими частями равенства и сделать так, чтобы в обеих частях равенства оказались одинаковые выражения.
Например, докажем, что равенство 0,5a × 5b = 2,5ab является тождеством.
Упростим левую часть этого равенства. Для этого перемножим числа и буквы по отдельности:
0,5 × 5 × a × b = 2,5ab
В результате небольшого тождественного преобразования, левая часть равенства стала равна правой части равенства. Значит мы доказали, что равенство 0,5a × 5b = 2,5ab является тождеством.
Из тождественных преобразований мы научились складывать, вычитать, умножать и делить числа, сокращать дроби, приводить подобные слагаемые, а также упрощать некоторые выражения.
Но это далеко не все тождественные преобразования, которые существуют в математике. Тождественных преобразований намного больше. В будущем мы ещё не раз в этом убедимся.
Видео:Урок 1 ЧИСЛОВЫЕ ВЫРАЖЕНИЯ 7 КЛАСССкачать

Выражения и уравнения — определение и вычисление с примерами решения
Содержание:
Видео:Числовые выражения. Алгебра, 7 классСкачать

Выражения и уравнения
Вы уже знаете, что такое буквенные выражения, и умеете их упрощать с помощью законов сложения и умножения. Например,
Пример:
Есть ли коэффициент в выражении 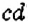
Вспомним, что преобразование выражения со скобками в выражение без скобок называется раскрытием скобок. Например:
Обратным действием в этом примере является вынесение общего множителя за скобки.
Слагаемые, содержащие одинаковые буквенные множители, называют подобными слагаемыми. С помощью вынесения общего множителя за скобки сводят подобные слагаемые:
Правила раскрытия скобок
Правила раскрытия скобок
- Если перед скобками стоит знак
, то при раскрытии скобок знаки слагаемых в скобках сохраняют;
- Если перед скобками стоит знак
, то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.
Пример:
Упростите выражение: 1) 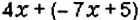
Решение:
1. Перед скобками стоит знак 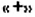
2. Перед скобками стоит знак 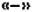
Для раскрытия скобок используют распределительное свойство умножения: 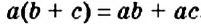
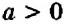
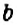
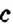
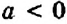
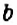
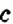
Пример:
Упростите выражение: 1) 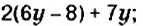
Решение:
1. Множитель 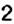
2. Множитель 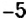
- Слово «сумма» происходит от латинского summа, что значит «итог», «общее количество».
- Слово «плюс» происходит от латинского plus, что значит «больше», а слово «минус» — от латинского minus, что значит «меньше». Знаки
и
используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
Уравнения. Основные свойства уравнений
Вы уже знаете, что такое уравнение, корень уравнения. Вспомним основные формулировки.
Определение:
Уравнением называется равенство, содержащее неизвестное, значение которого нужно найти.
Неизвестное число в уравнении обозначают буквой 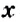
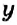
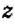
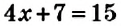
уравнением, где 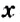
Определение:
Значение неизвестного, обращающее уравнение в верное числовое равенство, называется корнем уравнения.
Так, корнем уравнения 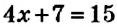
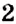
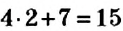
Уравнение может иметь больше одного корня. Например, уравнение 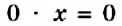
Уравнение может не иметь корней. Например, уравнение 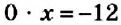
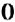
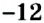
Определение:
Решить уравнение — значит найти все его корни или установить, что уравнение не имеет ни одного корня.
В 5 классе вы находили корень уравнения как неизвестный компонент арифметического действия. При решении более сложных уравнений опираются на свойства равенств. Рассмотрим основные из них.
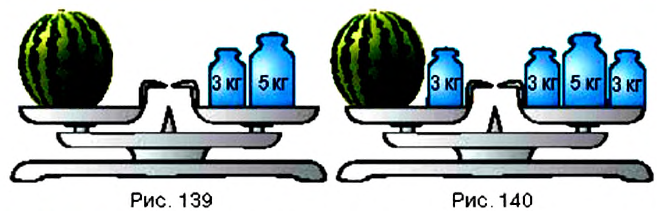
Посмотрите на рисунок 139. Вы видите, что на левой чаше весов находится арбуз неизвестной массы, а на правой — гири массой 5 кг и 3 кг. Если на обе чаши весов положить по гире массой 3 кг, то весы останутся в равновесии (рис. 140). Понятно, что, сняв эти гири или поставив навесы одинаковые гири другой массы, снова получим равновесие на весах. Этот пример иллюстрирует следующее свойство равенств.
Определение: Если к обеим частям равенства прибавить (из обеих частей равенства вычесть) одно и то же число, то равенство не изменится.
Пример:
Решите уравнение: 1) 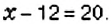
Решение:
К левой и правой частям уравнения прибавим число 12 и упростим полученное равенство:
Решая уравнение, в левой его части «уединили неизвестное». Такой же результат получим, если число 12 перенесём из левой части в правую, изменив при этом его знак.
Определение:
Слагаемое можно переносить из одной части уравнения в другую, изменяя знак этого слагаемого на противоположный.
Пример:
Можно ли переносить в другую часть уравнения слагаемое, содержащее неизвестное? Да.
Посмотрите на рисунок 141. Вы видите, что масса пакета муки равна 2 кг. Понятно, что масса трёх таких пакетов втрое больше (рис. 142). Этот пример иллюстрирует другое свойство равенств.
Определение: Если обе части равенства умножить (разделить) на одно и то же число, отличное от нуля, то равенство не изменится. 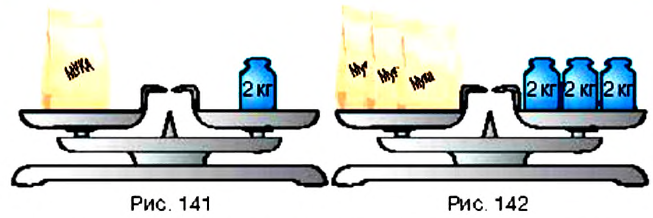
Пример:
Решите уравнение
Решение:
Чтобы избавиться от дробного коэффициента, умножим на 3 обе части уравнения:
Основные свойства уравнений
Основные свойства уравнений
- Корни уравнения не изменятся, если к обеим частям уравнения прибавить (из обеих частей уравнения вычесть) одно и то же число.
- Корни уравнения не изменятся, если обе части уравнения умножить (разделить) на одно и то же число, отличное от нуля.
Считают, что язык алгебры — это уравнения. «Чтобы решить вопросы. относящиеся к числам или к абстрактным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий И. Ньютон (1643-1727) в своём учебнике по алгебре, названном «Общая арифметика».
Применение уравнений к решению задач
В 5 классе с помощью уравнений вы решали задачи на нахождение суммы двух величин или их разности.
В 6 классе будем рассматривать особый вид задач — на равенство двух величин. В таких задачах тоже сравнивают две величины, например, количество книг на первой и второй полках. Значения же выражений с этими двумя величинами приравнивают.
Пример:
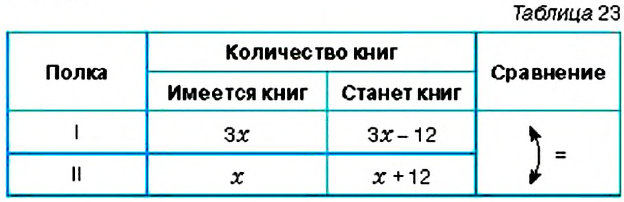
На первой полке книг в 3 раза больше, чем на второй. Если с первой полки переставить на вторую 12 книг, то на обеих полках их станет поровну. Сколько книг на каждой полке?
Решение:
Составим краткую запись задачи в виде таблицы 23
Пусть 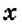
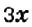
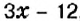
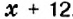
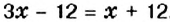
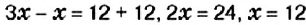

Первым произведением, содержащим исследование алгебраических вопросов, считают трактат «Арифметика» Диофанта (середина IV в.). Из 13 книг, составляющих полное собрание трудов Диофанта, до нас дошло только 6. В них предложено решение сложных алгебраических задач. Основная часть трактата — сборник задач (в первых шести книгах их 189) с решениями и удачно подобранными иллюстрациями к способам решения.
Перпендикулярные и параллельные прямые
Вы знаете, что прямая — это геометрическая фигура. Две прямые могут по-разному размещаться на плоскости. В 6 классе вы узнаете о перпендикулярных и параллельных прямых.
Перпендикулярные прямые
Посмотрите па перекрёсток дорог на рисунке 143. Вы видите, что дороги напоминают пересекающиеся прямые, которые образуют четыре прямых угла. В этом случае говорят, что прямые пересекаются под прямым углом. В тетради по математике клеточки образуются перпендикулярными прямыми.
Определение:
Две прямые на плоскости называются перпендикулярными, если они пересекаются под прямым углом.
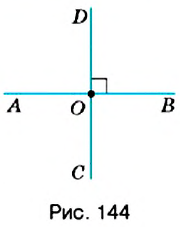
На рисунке 144 изображены прямые 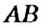
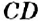

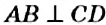
Если прямая 
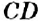

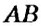
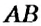
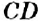
Пример:
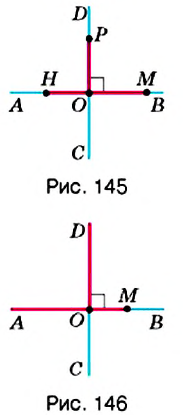
Бывают ли перпендикулярными отрезки? лучи? Да, если они являются частями соответствующих перпендикулярных прямых (рис. 145—146).
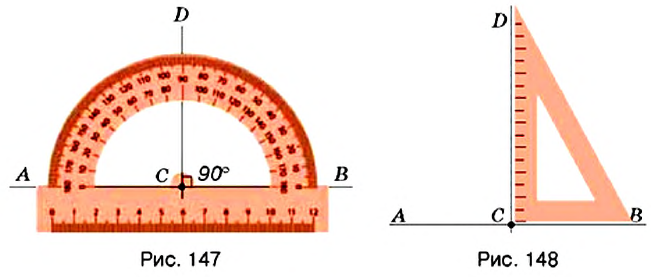
Для построения перпендикулярных прямых используют транспортир или угольник. На рисунке 147 вы видите, как строили прямую 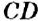

Параллельные прямые
Посмотрите на рисунок 149. Вы видите рельсы трамвайных путей, напоминающие прямые, которые лежат в одной плоскости и не пересекаются. Это пример параллельных прямых. Вокруг нас много других примеров параллельных прямых. Так, в тетради в клеточку горизонтальные линии параллельны. То же самое можно сказать и про вертикальные линии. Противоположные края парты, противоположные стороны оконной рамы, троллейбусные штанги также параллельны.
Определение:
Две прямые на плоскости называются параллельными, если они не пересекаются.
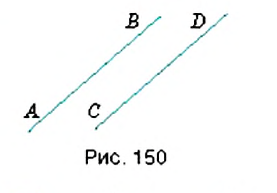
На рисунке 150 изображены параллельные прямые 


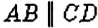


Если прямая 



Пример:
Бывают ли параллельными лучи? отрезки? Да, если они являются частями соответствующих параллельных прямых.
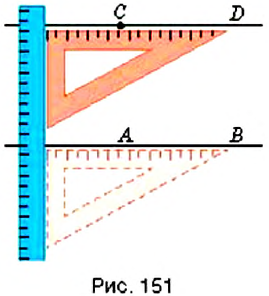
На рисунке 151 вы видите, как с помощью линейки и угольника через точку 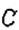


Название «перпендикулярный» происходит от латинского слова «perpendicufaris», которое означает «отвесный». Знак 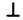
Название «параллельный» происходит от греческого слова «раralelos» — «идущий рядом». Символ параллельности 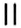
Координатная плоскость
Вы уже знаете, что такое координатная прямая (рис. 162). На ней точка 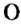
Однако на практике часто приходится пользоваться ориентирами не только вдоль прямой, но и на плоскости.
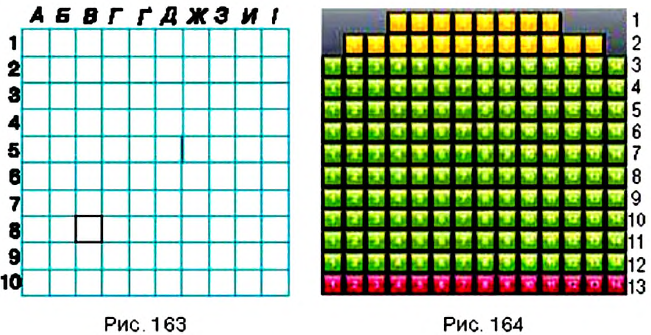
Вы знаете, что в игре «Морской бой» положение корабля определяют с помощью «координат» из цифр и «координат» из букв (рис. 163). В зависимости от выбранной буквы передвигаются на определённое количество клеточек вправо или влево, а цифра указывает, на сколько клеточек нужно сместиться вверх или вниз. Итак, место корабля на поле боя определяют двумя « координатами».
Чтобы определить место в зале кинотеатра, также нужно знать две «координаты»: номер ряда и номер кресла в этом ряду (рис. 164). Причём порядок «координат» в такой паре является строго определённым. Действительно, например, пары чисел 3 и 12 и 12 и 3 направят нас в совершенно разные места зала: в 3-й ряд на 12-е место или в 12-й ряд на 3-е место. В отличие от предыдущего примера, для ориентирования в зале кинотеатра порядок координат не меняют, поскольку неудобно сначала искать номер места в ряду, а лишь затем — сам ряд.
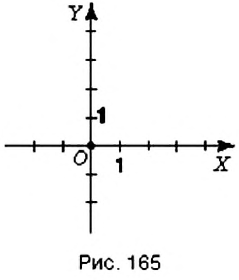
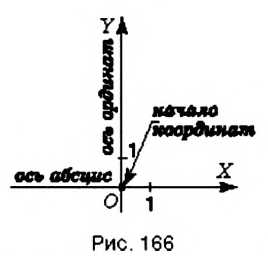
Итак, чтобы охарактеризовать размещение точки на плоскости, нужно задать две координатные прямые с равными единичными отрезками, одна из которых задаёт направление вправо-влево, а вторая — вверх-вниз. Для этого координатные прямые изображают перпендикулярно друг к другу и так, чтобы начала отсчёта на них совпадали (рис. 165). Одну из этих прямых (как правило, горизонтальную) считают первой, а другую — второй. Такая пара координатных прямых образует прямоугольную систему координат.
Первую координатную прямую называют осью абсцисс. Её обозначают 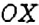
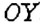
Плоскость с заданной на ней системой координат называют координатной плоскостью.
Каждой точке на плоскости можно поставить в соответствие пару чисел, взятых в определённом порядке, и наоборот, каждой паре чисел соответствует единственная точка координатной плоскости. Такая упорядоченная пара чисел называется координатами точки в данной системе координат. Координату по оси абсцисс называется абсциссой точки, а координату по оси ординат — ординатой точки.

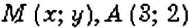
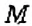
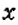
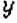
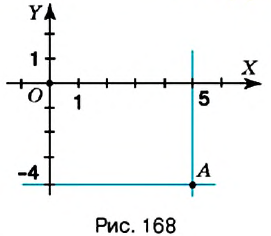
Пример:
На координатной плоскости постройте точку: 1) 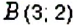
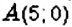
Решение:
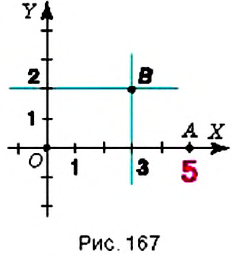
Введём прямоугольную систему координат на плоскости (рис. 167).
1. У точки 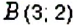
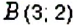
2. Поскольку ордината точки 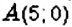
Обратите внимание:
- точка лежит на оси абсцисс, если её ордината равна нулю, и наоборот;
- точка лежит на оси ординат, если её абсцисса равна нулю, и наоборот;
- начало координат — точка
, имеет координаты
.
Пример:
Как определить координаты точки, построенной на координатной плоскости, например, точки 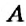
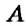
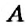
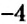
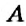
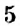
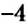
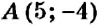
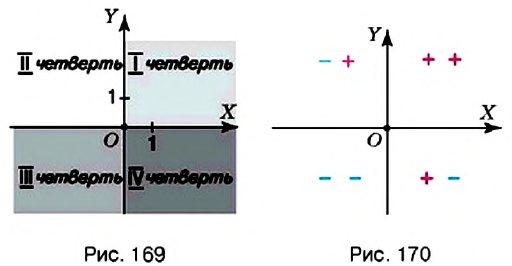
Координатные оси разбивают координатную плоскость на четыре части. Их называют координатными четвертями и обозначают так: I четверть, II четверть, III четверть, IV четверть (рис. 169).
Точки I четверти имеют положительную абсциссу и положительную ординату. И наоборот, если абсцисса и ордината точки положительные, то она лежит в I четверти, как, например, точка 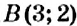
На рисунке 170 показаны знаки координат точек, лежащих в соответствующих четвертях.
Положение любой точки на поверхности Земли определяется двумя координатами: географической широтой и географической долготой.
Географические координаты ввёл древнегреческий учёный Гиппарх во И в. до н.э. Географические координаты применяют для определения положения точек земной поверхности относительно экватора и начального (нулевого) меридиана. Например, Киев имеет следующие географические координаты: 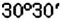
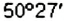
Графики зависимостей между величинами
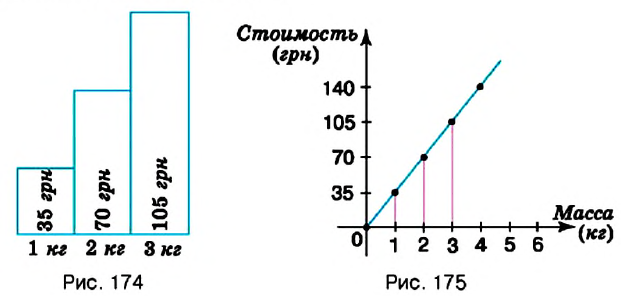
Вы знаете, что стоимость товара зависит от его количества: чем большее количество товара покупают, тем большей будет его стоимость. Например, если цена одного килограмма конфет составляет 35 грн, то за 2 кг нужно заплатить 70 грн, за 3 кг — 105 грн и т.п. Вы знаете, что такое соответствие можно наглядно отобразить на диаграмме (рис. 174). Однако по диаграмме трудно определить, сколько стоит 2,5 кг конфет или иное их количество. Изобразим данные о стоимости конфет не в виде столбиков, а вертикальными отрезками в системе координат (рис. 175). Поскольку величины «масса конфет» и «стоимость покупки» являются прямо пропорциональными, то верхние концы столбиков диаграммы можно соединить отрезками. Получим линию, показывающую, как изменяется стоимость покупки в зависимости от массы конфет. Такая линия называется графиком зависимости величины «стоимость покупки» от величины «масса конфет».
Обратите внимание:
все точки графика зависимости прямо пропорциональных величин лежат на одной прямой.
Вы знаете, что расстояние и время на его преодоление являются прямо пропорциональными величинами. Поэтому все точки графика движения лежат на одной прямой.
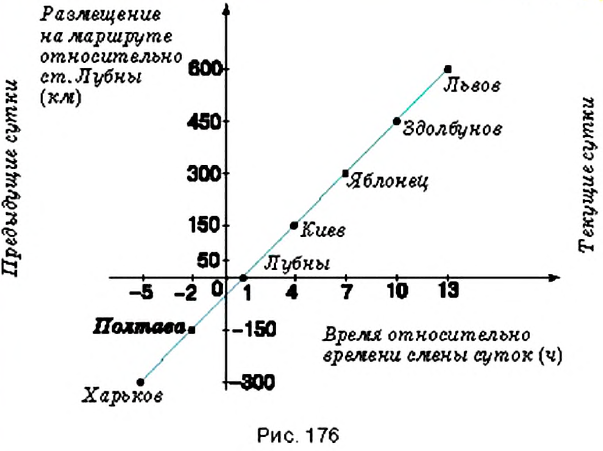
Пример:
Поезд Харьков — Львов выходит из Харькова около 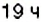
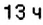
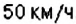
1) В котором часу новых суток поезд делает первую остановку? Какая это станция?
2) Что показывает число 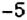
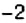
3) На каких расстояниях от первой остановки поезд останавливается на других станциях?
4) Что показывает число 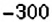
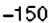
5) Каковы координаты конечных точек маршрута?
Решение:
По условию задачи, движение поезда начинается в 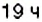
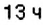
1. Начало новых суток поезд встречает недалеко от станции Лубны, а первую остановку делает в 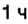
2. Поскольку движение поезда началось в предыдущие сутки, то по оси абсцисс время его отправления из Харькова можно выразить отрицательным числом 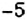
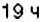
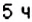
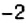
3. Остановки запланированы через каждые 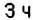
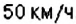
4. При помощи отрицательных чисел 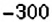
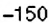
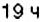
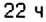
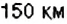
5. Конечные результаты точки маршрута поезда имеют координаты 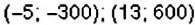
Пример:
Обязательно ли выбирать конечные точки маршрута для построения графика движения? Нет. График можно построить по любым двум его точкам. Но концы маршрута нужно отметить обязательно.
Обратите внимание:
график движения является прямой (или её частью), поэтому такой график можно построить по любым двум его точкам.
С помощью графиков можно решать целый класс задач. Рассмотрим задачу.
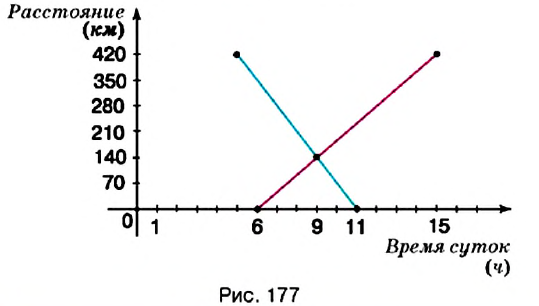
Пример:
Из пунктов 
Решение:
Построим в прямоугольной системе координат графики движения автомобилей (рис. 177). Красный отрезок — график движения красного автомобиля, синий — синего автомобиля. Точке пересечения этих отрезков соответствует время — 9 ч. Итак, автомобили встречаются в 9 ч.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
- Многочлены
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними
- Делимость натуральных чисел
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 2 ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Уравнения
Уравнение
Уравнение – это равенство, в котором есть неизвестное.
Если мы заменим любой компонент выражения неизвестным, мы получим уравнение.
Например, из выражения 6 + 7 = 13 можно сделать уравнение:
Неизвестное число обозначается маленькой латинской буквой:
Схемы уравнения
Мы видим, что из неизвестного числа х и 5 получается число 9. Целое – это 9.
Решение уравнений
Решить уравнение – это значит найти такое значение неизвестного числа, при котором это равенство станет верным.
х + 5 = 9
В данном уравнении неизвестно первое слагаемое. Чтобы найти неизвестное первое слагаемое, нужно из суммы вычесть известное второе слагаемое.
5 + х = 9
В данном уравнении неизвестно второе слагаемое. Чтобы найти неизвестное второе слагаемое, нужно из суммы вычесть известное первое слагаемое.
9 — х = 5
В данном уравнении неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемое вычесть разность.
х — 4 = 5
В данном уравнении неизвестно уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно из к разности прибавить вычитаемое.
Поделись с друзьями в социальных сетях:
🎬 Видео
Урок 5 ТОЖДЕСТВА. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ 7 КЛАСССкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

Алгебра 7 класс (Урок№13 - Числовые выражения.)Скачать

Выражения с переменными. Алгебра, 7 классСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Упрости выражения и найди их значения при х равномСкачать

Порядок выполнения действий в выражениях. Числовые выраженияСкачать

Буквенное выражение. Вычисление значений буквенных выражений при заданных значениях букв.Скачать

7 класс, 1 урок, Числовые и алгебраические выраженияСкачать

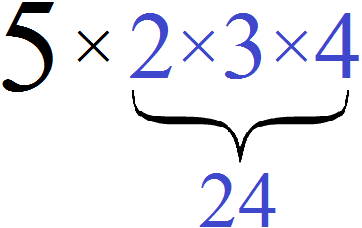
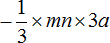
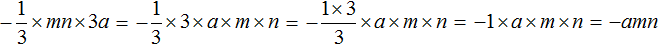
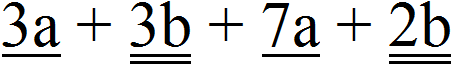
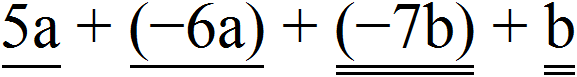
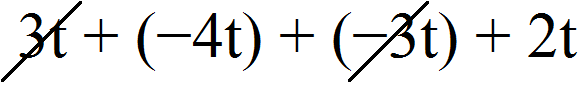
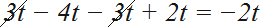
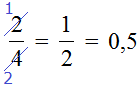
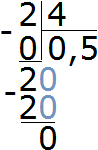
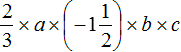
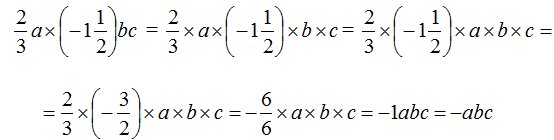
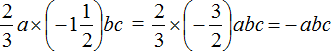
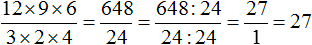
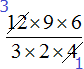
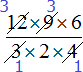
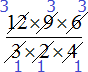
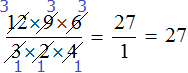
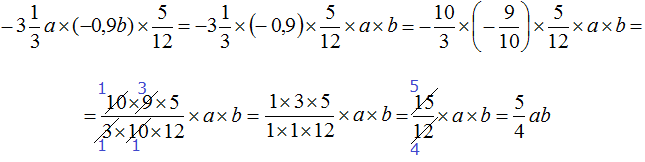
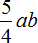
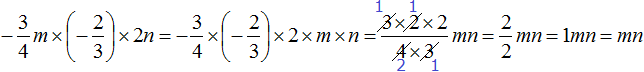
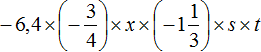
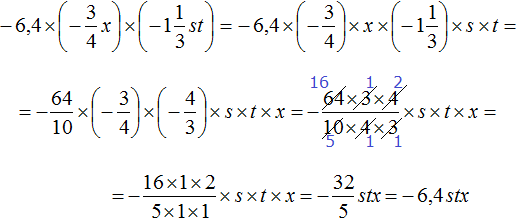
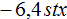
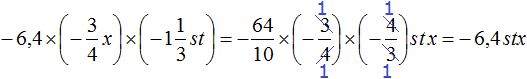
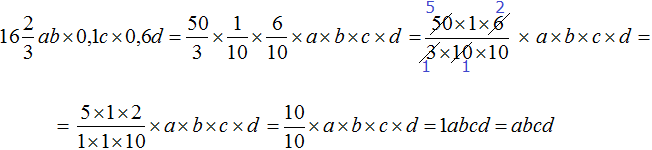
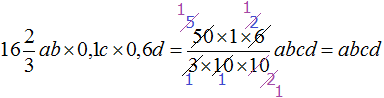


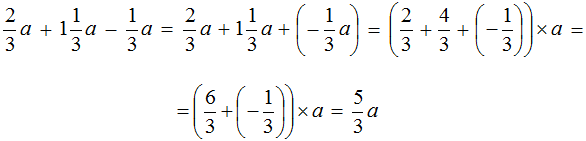
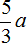
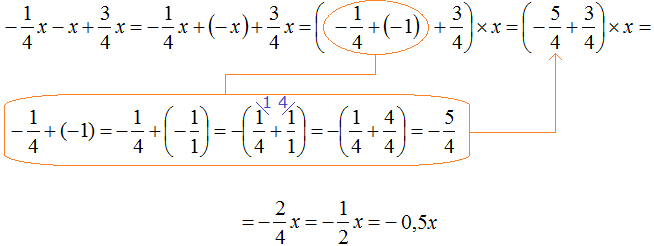
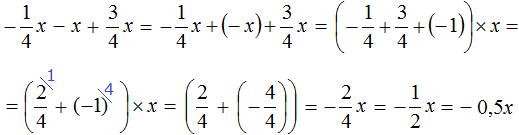
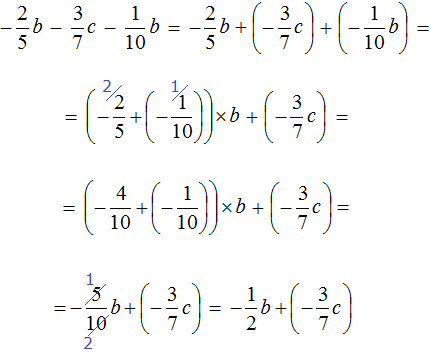
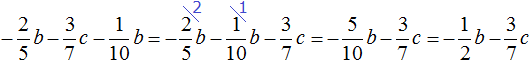
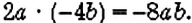
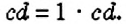
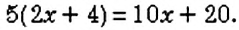
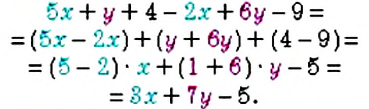
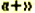 , то при раскрытии скобок знаки слагаемых в скобках сохраняют;
, то при раскрытии скобок знаки слагаемых в скобках сохраняют; , то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.
, то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.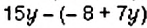
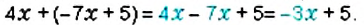
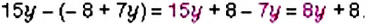
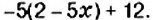
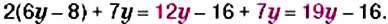
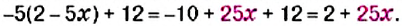
 и
и  используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
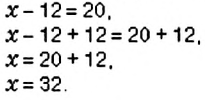
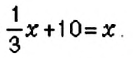
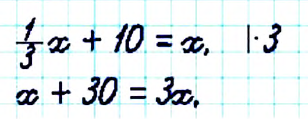
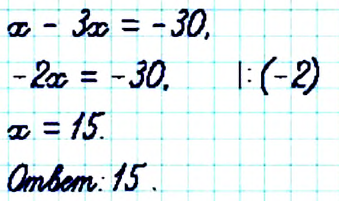




 , имеет координаты
, имеет координаты 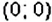 .
.