Определение скорости звука методом стоячих волн уравнение стоячей волны (7 видео)

В воздухе методом стоячей волны (или методом резонанса)

Определение скорости звука

В воздухе методом стоячей волны

(или методом резонанса)

Заведующий кафедрой ЕН и ОТД:

Проф. Даутов А.И.

Составил: доцент Авдонина Н.А.

Определение скорости звука

в воздухе методом стоячей волны (или методом резонанса)

Приборы и принадлежности:Звуковой генератор (ЗГ), динамик, стеклянная трубка, резервуар с водой, стойка с масштабной линейкой.

Любая частица среды, выведенная из положения равновесия, под действием упругих сил, стремится возвратиться в первоначальное положение и совершает колебания. Колебания этой частицы не остаются локализованными – начинают колебаться соседние с ней частицы, затем следующие и т.д. Такое распространение колебательного процесса в среде называется волной. Смещение частиц в волне в зависимости от времени колебания и положения частиц описывается уравнением волны, имеющий вид:

, (1)

где S – смещение частиц от положения равновесия;

r – расстояние частиц от источника колебаний;

v – скорость распространения волны;

T – период колебаний;

– круговая частота;

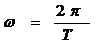
Уравнение (1) называется уравнением бегущей волны.

Волна, приходящаяся на границу двух сред, частично проходит через нее и частично отражается от нее. Если волна отражается от среды менее плотной, она меняет свое направление на обратное, причем никакого изменения фазы волны в точке отражения не происходит.

Если волна отражается от среды более плотной, то, изменив свое направление на обратное, она меняет свою фазу на противоположную. При сложении двух волн (падающей и отражающей), идущих навстречу друг другу, получаем стоячую волну. Это один из случаев интерференции волн.

Рассмотрим случай, когда отраженная волна имеет практически туже амплитуду, что и падающая. Эти волны отличаются только направлением скорости.

Уравнение падающей волны:

.(2)

Уравнение отраженной волны:

. (3)

Результирующее колебание любой точки среды будет получаться в результате сложения этих двух волн.

Уравнение результирующей волны, называемой стоячей, будет:

. (4)

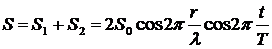
Множитель выражает амплитуду.

Таким образом, амплитуда колебания зависит от координаты r, определяющей положение точек среды. В определенных точках амплитуда стоячей волны равна сумме обоих слагаемых колебаний, такие точки называются пучностями, в других точках результирующая амплитуда равна нулю, эти точки называются узлами стоячей волны.

Определим координаты точек пучностей и узлов.

Наибольшее значение амплитуда принимает при .

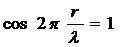
Отсюда, положение пучностей определяется условием:

(n=0,1,2,3,…)

Следовательно, координаты пучностей равны:

(n=0,1,2,3,…) (5)

Расстояние между соседними пучностями получим, если возьмем разность двух значений r, определяемых формулой (5) для двух последовательных значений n, откуда

т.е. расстояние между двумя соседними пучностями равно половине длины тех волн, в результате интерференции которых образуется данная стоячая волна.

В узлах амплитуда результирующего колебания будет минимальной, т.е.:

или .

Следовательно, координаты узлов:

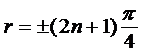
Длина стоячей волны равна длине бегущей волны. Она равна удвоенному расстоянию между соседними пучностями или между двумя соседними узлами.

У стоячей волны все точки между соседними узлами имеют одинаковые фазы. При переходе через узел фаза меняется скачком на 180°, т.е. смещения соседних участков, разделенных узлом, направлены в противоположные стороны.

Графически результирующая волна имеет вид, представленный на рис. 1, где сплошной линией изображена падающая волна, пунктирной – отраженная волна.

Образование стоячих волн происходит обычно при интерференции бегущей вперед и отраженной волны. На границе отражения может образоваться или узел, или пучность. Это зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, более плотная, чем среда, в которой распространяется волна, то на границе получается узел. В этом случае, в месте отражения волна меняет фазу на противоположную. Если среда, от которой происходит отражение, менее плотная, чем среда, в которой распространяется волна, то на границе получается пучность. В данном случае волна не меняет фазы.

Стоячая волна, в частности, получается при распространении продольных волн в цилиндрической трубе, закрытой с одного конца. Распространение звука в газах (а значит и в воздухе) осуществляется продольными волнами.

Продольной волной называется волна, колебания частиц которой совпадает с направлением распространения волны. Такие волны образуются также в жидкостях и твердых телах.

Если же колебания частиц перпендикулярны направлению распространению волны, то это будет поперечная волна. Поперечные волны образуются лишь в твердых телах, т.е. в телах, которые обладают деформацией сдвига – упругостью сдвига.

При возбуждении колебаний в одном теле колебаниями другого можно наблюдать явления резкого возрастания амплитуды колебаний. Такое явление называется резонансом.

Резонанс наблюдается в том случае, когда частота собственных колебаний совпадает с частотой вынужденных колебаний.

Можно заставить резонировать на звук воздушный столб, заключенный в высоком цилиндре, в который налита вода.

Изменяя уровень воды в цилиндре, можно добиться того, что собственный период колебания воздушного столба станет одинаковым с периодом колебания генератора. Такой воздушный столб сильно резонирует на доходящие до него звуки, в нем образуется стоячая волна.

Сила звука резко усиливается, т.е. наступает резонанс.

Расстояние между пучностями и любым узлом в стоячей волне, как известно, может составить (рис. 1).

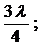
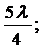
Следовательно, резонанс будет возникать каждый раз, когда длина воздушного столба равна нечетному числу четвертей длины звуковой волны (рис. 2).

Если обозначить длину резонирующего столба воздуха через L то можем написать уравнение:

(n=0,1,2,3,…)

Расстояние между последовательными максимумами определяется соотношением.

(n=0,1,2,3,…) (6)

(7)

(8)

, (9)

где v₀ – скорость при 0°С; v – при t°С.

Описание установки

Приборы, резонирующие на какой-либо звук, называются резонаторами. В работе резонатором является прибор (рис. 3), состоящий из длинной стеклянной трубки АД и резервуара, соединенных между собой длинной резиновой трубкой, укрепленных на стойке и заполненных водой.

Поднимая или опуская резервуар С,поднимают или опускают тем самым уровень воды в трубке АД.

Воздушный столб при этом плавно меняет свою высоту, начиная с небольших значений (положение В) и кончая высотой, равной длине почти все стеклянной трубки АД (положение Д).

Содержание

Определение скорости звука методом стоячих волн
ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА
Таблица 1
ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ И ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА МЕТОДОМ СТОЯЧЕЙ ВОЛНЫ
📹 Видео

Видео:Урок 378. Методы определения скорости звука в воздухеСкачать

Определение скорости звука методом стоячих волн

На правах рукописи

Федеральное агентство по образованию

Кафедра физики

ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА

МЕТОДОМ СТОЯЧИХ ВОЛН

Методические указания к лабораторной работе № 55

Определение скорости звука методом стоячих волн: Метод. указания к лабораторной работе / Сост. ; ВолгГАСА, Волгоград. 2002, 9 с.

Целью настоящей работы является измерение скорости звука в воздухе. Дано определение стоячей волны, рассмотрен механизм образования стоячей волны. Рассмотрена методика определения скорости звука методом стоячих волн. Описан порядок выполнения работы. Даны правила техники безопасности и приведены контрольные вопросы.

Для студентов всех специальностей по дисциплине «Физика»

Ил. 3. Табл. 2. Библиогр. 4 назв.

Цель работы ─ измерение скорости звука в воздухе.

Приборы и принадлежности: звуковой генератор, измерительная труба с микрофоном и телефоном.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Целью работы является определение скорости звука методом стоячих волн. Звук – это упругие волны, воспринимаемые ухом человека (обычно в частотном диапазоне от 20 Гц до 20 кГц). Упругие волны с частотой менее 20 Гц называются инфразвуком, с частотой более 20 кГц – ультразвуком.

Независимо от того, является ли упругая волна продольной или поперечной, ее распространение описывается уравнением бегущей волны для некоторой величины, характеризующей колебательный процесс, которая называется смещением Для волн в твердом теле – это смещения колеблющихся частиц (поперечные волны), для продольных волн в жидкости или газе величиной обозначают избыточное давление колеблющейся среды (отклонение от равновесного давления). Уравнение плоской гармонической бегущей волны, распространяющейся в положительном направлении оси OC в отсутствие поглощения, имеет вид ,где – амплитуда бегущей волны (величина постоянная), – фаза плоской волны, – начальная фаза колебаний (в точке с в момент времени – циклическая частота (ν – частота, Τ – период колебаний), k – волновое число где λ – длина волны. Длиной волны λ называется расстояние, на которое распространяется гармоническая волна за время, равное периоду колебаний: , где υ – скорость волны, называемая фазовой скоростью. Эту величину определяют в данной работе. Экспериментальное значение υ надо сравнить с теоретическим.

Если две различные когерентные волны, исходящие из разных источников, перекрываются в некоторой области, то в области перекрытия волн колебания налагаются друг на друга, происходит сложение (интерференция) волн, в результате чего колебания в одних местах получаются более сильные, а в других более слабые.

Особым примером интерференции двух волн служат стоячие волны. Стоячие волны возникают в результате сложения двух волн, движущихся в противоположных направлениях. Одна из них – это волна, возбуждаемая источником и распространяющаяся вдоль оси абсцисс; ее уравнение имеет вид

. Вторая волна возникает вследствие отражения первой волны от преграды и распространяется в направлении отрицательных значений оси абсцисс, что приводит к изменению знака при координате. Кроме того, следует учесть, что при отражении фаза волны может меняться. Уравнение отраженной волны имеет вид: .

Уравнение стоячей волны запишется следующим образом: .

После элементарных преобразований получится: , (1)

где амплитуда стоячей волны определяется выражением

(2)

Так как все точки стоячей волны колеблются одновременно, но с разными амплитудами, то находящиеся в покое (нулевая амплитуда) называются узлами стоячей волны; области, колеблющиеся с максимальной амплитудой, – пучностями.

Полагая, что можно определить координаты узлов. Из условия следует: где целое число n = 0, 1, 2, 3… . Учитывая, что координата узлов имеет вид

(3)

Координаты пучностей находятся из условия отрицательный знак при амплитуде означает, что при переходе через узел фаза стоячей волны меняется на противоположную, итак, для пучностей следовательно, Выразив вновь волновое число k через длину волны получим: (4)

Определение скорости звука методом стоячих волн уравнение стоячей волны

Так как амплитуда стоячей волны при переходе через нулевое значение меняет знак, в соответствии с этим фаза колебаний по разные стороны от узла отличается на π, т. е. точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключенные между соседними узлами, колеблются в одной фазе. На рис. 1 показан ряд «моментальных фотографий» отклонения точек от положения равновесия.

Рис. 1. Схема образования стоячей волны

Первая фотография соответствует моменту, когда отклонения достигают наибольшего абсолютного значения. Последующие «фотографии» сделаны с интервалами в четверть периода. Стрелками показаны скорости частиц.

Из опытов было установлено, что скорость звука зависит только от давления и плотности газа т. е.

(5)

Из уравнения Клапейрона – Менделеева плотность газа можно определить следующим образом:

(6)

где – молярная масса газа; – его абсолютная температура, – универсальная газовая постоянная.

Подставив выражение (6) в выражение (5), получим

; (7)

Учитывая, что процессы сжатия и разряжения газа при звуковых колебаниях протекают очень быстро, то с большой степенью точности могут считаться адиабатными. Можно для скорости распространения звука в воздухе получить выражение:

; (8)

где γ – отношение теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.

;

Из формулы (8) следует, что скорость звука в газе обратно пропорциональна корню квадратному из молярной массы. Следовательно, с наибольшей скоростью распространяется звук в водороде. Зависимость скорости звука в м/с от молярной массы и температуры приведена в таблице.

Видео:Стоячие волны. 11 класс.Скачать

Таблица 1

Видео:Урок 375. Стоячие волныСкачать

ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ И ПОКАЗАТЕЛЯ АДИАБАТЫ ВОЗДУХА МЕТОДОМ СТОЯЧЕЙ ВОЛНЫ

Цель работы: исследование упругих и тепловых свойств воздуха.

Оборудование: труба с подвижной стенкой на одном из концов, звуковой генератор, электронный осциллограф, термометр.

Введение.

Скорость распространения звуковых волн в среде определяется, в первую очередь, упругими свойствами этой среды. Газы обладают только объемной упругостью. Поэтому в них могут распространяться только продольные волны, в которых чередуются области сгущения и разрежения газа. Скорость звука , в общем случае, определяется выражением

(1)

где P– давление в газе; – плотность газа.

Лаплас установил, что в звуковой волне в газе колебания происходят настолько быстро, что теплообмен между областями разрежения и сгущения не имеет места, Распространение звука в газе – адиабатический процесс. Уравнение Пуассона для адиабатического процесса:

(2)

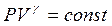
где 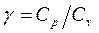– показатель адиабаты; C_p – теплоемкость при постоянном давлении; C_v–теплоемкость при постоянном объеме; V – объем. Если учесть, что плотность пропорциональна 1/V, то для дифференциала левой части (2) получается:

(3)

Отсюда скорость звука в газе:

(4)

Из уравнения состояния идеального газа в форме:

(5)

(где M – молярная масса газа; R –универсальная газовая постоянная, Т – абсолютная температура) и соотношения (4) следует формула для показателя адиабаты:

(6)

Формула (6) используется в данной лабораторной работе для определения показателя адиабаты воздуха.

Скорость звука определяется методом стоячей волны. Стоячая волна образуется, например, при положении двух плоских гармонических волн, бегущих в противоположных направлениях по оси X:

и (7)

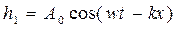
где h₁,h₂ – смещение частиц среды в первой волне и во второй волне соответственно; A₀ – амплитуда колебаний; – циклическая частота; k – волновое число. Результирующая волна имеет вид:

(8)

где – длина волны звуковой.

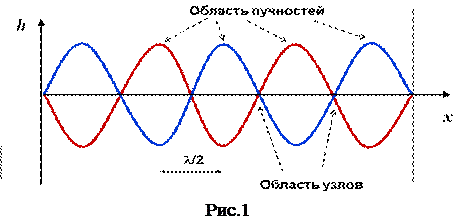Это стоячая волна (рис.1), которая характеризуется, как следует из формулы (8), чередующимися пучностями и узлами. В местах расположения пучностей амплитуда стоячей волны максимальна, в местах расположения узлов амплитуда стоячей волны равна нулю.

Расстояние между соседними узлами и между соседними пучностями одинаково и равно:

. (9)

Таким образом, длина звуковой волны может быть найдена по измеренным значениям . Скорость звука v, в свою очередь, можно рассчитать по формуле

, (10)

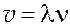
где – частота звуковой волны. Окончательно для скорости звуковой волны получается выражение

, (11)

которое и используется в данной лабораторной работе для определения скорости звука в воздухе.

Описание установки.

Схема установки представлена на рисунке. Звуковая волна создается в длинной стеклянной трубке 1, с одной подвижной стенкой М. Вдоль трубы расположена линейка 2. В неподвижной стенке трубы укреплен телефон Т, соединенный со звуковым генератором ЗГ. В под вижной стенке трубы укреплен регистрирующий микрофон, соединенный с входом электронного осциллографа ЭО. В стеклянной трубке происходит наложение бегущей волны от телефона Т и отраженной волны от подвижной стенки М. Результирующая волна – стоячая.

Порядок выполнения работы.

1. Включить звуковой генератор и осциллограф.

2.После прогрева приборов установить на звуковом генераторе частоту волны и необходимую амплитуду сигнала (по указаниям преподавателя).

3. Установить для удобства регистрации необходимую частоту развертки осциллографа. Перемещая подвижную стенку М, убедиться, что на экране осциллографа отчетливо видны максимальный по величине сигнал (пучность) и минимальный сигнал (узел).

4. Измерить координаты всех узлов и пучностей вдоль стеклянной трубки. Измерить температуру воздуха.

5. Вычислить среднее значение расстояния между узлами и пучностями.

6. Вычислить среднее значение скорости звука и среднее значение показателя адиабаты воздуха, используя формулы (6) и (11). Рассчитать погрешности измерения и .