Определение скорости и ускорения точки по заданным уравнениям ее движения онлайн калькулятор (5 видео)

Ускоренное движение тела

Темп изменения скорости называется ускорением. Другими словами, если скорость возрастала на одну и ту же величину в единицу времени, то такое движение называется движение с равномерным ускорением.

Найти ускорение движения тела

Расстояние, ускорение, скорость

Содержание

Какое бывает ускорение
Путь, скорость и ускорение
Задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения
Скорость, время и ускорение
📸 Видео

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Какое бывает ускорение

Ускорение бывает равномерное, положительное и отрицательное.

Если скорость изменяется (возрастает или убывает) равномерно, то ускорение называется равномерным;
Если скорость возрастает, то ускорение положительно;
Если скорость убывает, то ускорение отрицательно.

Формула для нахождения ускорения: a=v/t

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Путь, скорость и ускорение

Формула v=at дает соотношение между скоростью, ускорением и временем, а формула S = at 2 /2 дает соотношение между путем, ускорением и временем. До сих пор, однако, мы не имели соотношения между путем S, скоростью и и ускорением а. Один из способов вывести это соотношение заключается в подстановке t 2 , выраженного через v и а, в формулу S = at 2 /2. Решая относительно t формулу v=at, мы получим t=v/a. Возведя обе части в квадрат: t 2 =v 2 /a 2 , подставляя v 2 /a 2 вместо t 2 , имеем

v 2 = 2aS

Скорость автомобиля 90 см/сек. Через 3 сек его скорость равна нулю. Найдите его отрицательное ускорение (темп равномерного уменьшения скорости).

a=-v/t

a=-90/3=-30 см/сек. за 1 сек.

Ответ можно записать и так: 30 см/сек 2 , это будет означать, что автомобиль уменьшает свою скорость на 30 см/сек за каждую секунду.

Видео:Кинематика точки Задание К1Скачать

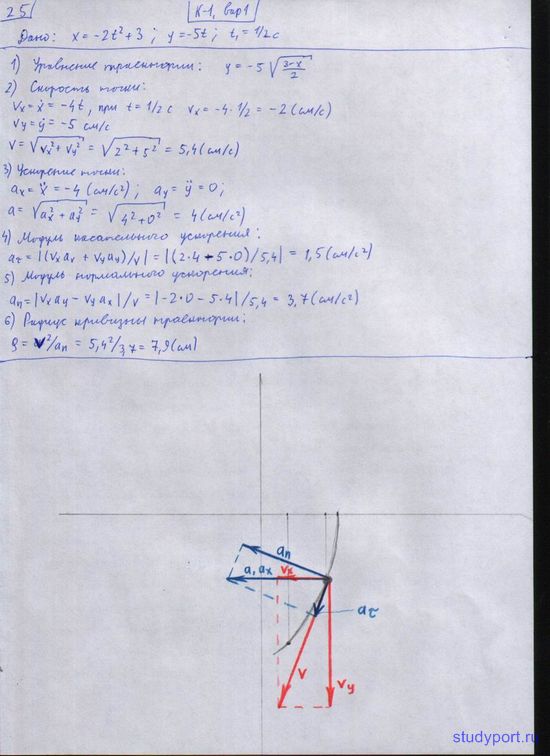
Задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения

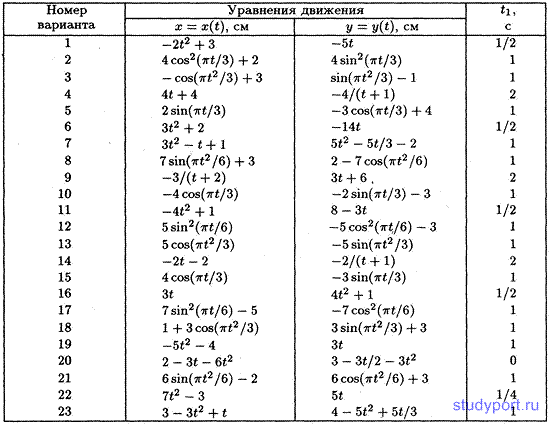
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t₁ (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Необходимые для решения данные приведены в таблице.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Термех. Кинематика. Определение скорости и ускорения точек плоского механизма...Скачать

Скорость, время и ускорение

Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:

V = V0 + а*t

V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.

Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
Если V0 = 0, то V = а*t.

Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.

t = (V — V0) / а

Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:

а = (V — V0) / t

а = (V0 — V) / t

Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).

Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δ v, полученный результат делим на разницу между временем Δ t.(начальным и конечным) :

а = Δ v / Δ t

Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.