Определение системы и совокупности уравнений и неравенств как логического понятия (7 видео)

Совокупности уравнений, неравенств, систем и т.п.

Вообще в школьных учебниках алгебры о совокупностях информации очень мало. Про совокупности упоминается лишь вскользь, да и то в старших классах. С нашей точки зрения это не очень справедливо хотя бы потому, что использование совокупностей довольно удобно при оформлении решений уравнений, неравенств и их систем. Давайте восполним этот пробел.

Ниже представлен материал, дающий общее представление о совокупностях уравнений, неравенств, систем и их всевозможных комбинаций. Здесь вы найдете определения совокупностей и их решений, принятые обозначения, а также поясняющие примеры.

Навигация по странице.

Содержание

Что такое совокупность уравнений, неравенств, систем?
Что называется решением совокупности?
Совокупности уравнений, неравенств, систем: определение, как решить
Понятие совокупности
Что такое решение совокупности
Решение совокупностей неравенств с одной переменной
Понятие совокупности неравенств с одной переменной и его решения
Алгоритм решения системы неравенств с одной переменной
Сравнение систем и совокупностей неравенств
Примеры
📹 Видео

Видео:Как решать совокупность неравенствСкачать

Что такое совокупность уравнений, неравенств, систем?

Сразу скажем, что если у Вас сформировано четкое представление о системах уравнений и системах неравенств, то определения совокупностей воспримутся очень легко. Прочитав их, Вы сразу почувствуете, будто уже их встречали.

Информация из учебников [1, с. 24; 2, с. 129; 3, с. 64-65] позволяет записать следующее определение совокупности уравнений:

Совокупностями уравнений называются записи, представляющие собой несколько расположенных друг под другом уравнений, которые слева объединены квадратной скобкой, и обозначающие множество всех таких решений, которые являются решениями хотя бы одного из уравнений совокупности.

Давайте проведем параллель между системами и совокупностями. Системы записывают с помощью фигурной скобки, а совокупности – с помощью квадратной, системы обозначают множество решений, которые являются решениями каждого уравнения системы, а совокупности – множество решений, которые являются решениями хотя бы одного уравнения совокупности.

Для наглядности приведем примеры совокупностей уравнений: , .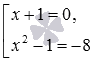

Здесь заметим, что в школе при записи совокупностей часто не используют квадратную скобку, а просто перечисляют через запятую составляющие этой совокупности. Так последняя совокупность из предыдущего абзаца может быть записана как x+y 2 +z 4 =0 , x·y·z=0 , z=5 .

Аналогично определяется и совокупность неравенств:

Совокупность неравенств – это запись, представляющая собой несколько записанных одно под другим неравенств, объединенных слева квадратной скобкой, и обозначающая множество решений, являющихся решениями хотя бы одного из неравенств совокупности.

Это определение находится в согласии с описанием совокупностей неравенств, приведенным в учебнике Мордковича [1, с. 222] .

Вот пример совокупности неравенств .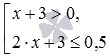

При описании совокупностей при надобности можно уточнять число составляющих их уравнений и неравенств, число переменных и вид уравнений и неравенств. К примеру, совокупность из предыдущего абзаца – это совокупность двух неравенств с одной переменной x , причем составляющие ее неравенства – целые рациональные первой степени.

Под знак совокупности можно поместить не только уравнения или неравенства по отдельности. Есть смысл рассматривать, например, совокупность уравнения и двух неравенств, неравенства и системы уравнений, совокупность двух систем неравенств и т.п. При этом главное сохранять смысл, заключающийся в совокупности, — она означает множество решений, являющихся решением хотя бы одного объекта совокупности.

Для примера приведем совокупность двух систем неравенств и совокупность такого вида .

Видео:Решение системы неравенствСкачать

Что называется решением совокупности?

К совокупностям непосредственно относятся их решения. Дадим определения решений совокупностей с одной переменной, а также с двумя, тремя и большим числом переменных.

Решением совокупности с одной переменной называется такое значение переменной, которое является решением хотя бы одного составляющего элемента совокупности.

Например, если речь идет о совокупности уравнений с одной переменной, то решение совокупности – это значение переменной, которое является решением хотя бы одного составляющего ее уравнения. Так x=3 – это решение совокупности неравенств , так как 3 является решением первого неравенства. А вот нуль не является решением записанной совокупности, так как это значение не является решением ни одного неравенства совокупности, действительно, 0>1 и 0 2 ≥4·0+2 – неверные числовые неравенства.

Решением совокупности с двумя, тремя и большим числом переменных называется двойка, тройка и т.д. значений переменных, являющаяся решением хотя бы одного объекта совокупности.

В качестве примера рассмотрим следующую совокупность . Пара значений (3, 0) есть решение этой совокупности, так как она является решением системы , потому что 3+0>0 и 3≥3 — верные неравенства. А пара значений x=−1 , y=2 не является решением совокупности, так как она не является решением ни уравнения x 2 +y 2 =4 , ни системы неравенств .

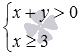
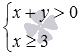
Иногда используются термины «частное решение совокупности» и «общее решение совокупности». Под частным решением совокупности понимают одно отдельно взятое решение, а общим решением называют множество всех частных решений совокупности. Но чаще говорят просто о решении совокупности, а уже из контекста черпают дополнительную информацию, о частном или об общем решении идет речь.

В заключение заметим, что из определения совокупности и ее решений следует такой вывод: решение совокупности есть объединение решений всех элементов, составляющих совокупность. А решение систем, напомним, есть пересечение решений всех ее элементов.

Продолжить изучение темы рекомендуем материалом статьи равносильные совокупности.

Видео:Система и совокупность. Как решать неравенстваСкачать

Совокупности уравнений, неравенств, систем: определение, как решить

Тема совокупностей уравнений и др. систем, как правило, в рамках школьного курса представлена скупо. В 10-11 классе она изучается совсем недолго. Мы считаем, что это неверный подход, поскольку совокупности — прекрасный способ оформления привычных решений при работе с неравенствами и уравнениями, поэтому в рамках статьи мы раскроем этот вопрос.

В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Понятие совокупности

Для того, чтобы хорошо понимать, что такое совокупность уравнений, нужно вспомнить еще одно понятие из школьного курса алгебры — система уравнений (аналогично неравенствам). Тогда определения совокупности покажутся вам знакомыми и легко усвоятся.

Проанализировав несколько учебников, выберем наиболее удачное определение:

Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.

Сравним между собой понятие совокупности и понятие системы:

Запись совокупности, как мы уже говорили выше, осуществляется с помощью квадратной скобки, а системы записываются с фигурной.
Совокупность включает в себя множество решений, которые относятся хотя бы одному из уравнений, входящих в ее состав. Система объединяет решения, которые подходят для каждого уравнения.

Пример 1

Вот примеры совокупности уравнений:

x + 1 = 0 , x 2 — 1 = — 8 x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5

Иногда при записи совокупности можно обойтись и без квадратной скобки: так часто делают в школе. В таком случае уравнения можно просто указать через запятую. Для примера выше это может быть запись вида x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5 .

Понятие совокупности неравенств формулируется схожим образом.

Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратной скобкой. Она включает в себя решения, которые подходят хотя бы для одного из неравенств, входящих в состав совокупности.

Приведем пример такой записи:

x + 3 > 0 , 2 · x + 3 ≤ 0 , 5

Схожее определение для этого понятия упоминается в учебнике Мордковича.

Если необходимо, то можно указать, сколько уравнений (неравенств) входят в состав совокупности, а также сколько в ней участвует переменных. Вид уравнения (неравенства) также может быть внесен в запись при необходимости. Сформулируем название совокупности из примера: это совокупность 2-х неравенств с одной переменной, а ее составные части — это целые рациональные первой степени.

Сочетать в рамках одной совокупности можно не только записи одного вида. Так, имеет право на существование совокупность, состоящая из двух неравенств и одного уравнения, сочетание одного неравенства с системой уравнений, двух систем неравенств и др. Главная задача — сохранить неизменным основной смысл совокупности: в нее входят такие решения, которые подходят хотя бы для одной составляющей совокупности.

В качестве примера смешанных совокупностей приведем две:

x > 3 x 8 x — 5 x ≤ — 2 x 2 = 9 x 2 > 5 ( x — 6 ) · ( x — 8 ) = 0 x ≤ 3 x 2 + 2 · x — 8 > 0

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Что такое решение совокупности

Решение — главная составляющая совокупности. Сформулируем, что же такое решения совокупности с разным количеством переменных.

Решение совокупности с одной переменной представляет собой значение этой переменной, которое является решением хотя бы одной составляющей совокупности (уравнения, неравенства).

Если мы возьмем совокупность уравнений, значит, его решение — это значение x , при котором хотя бы одно из уравнений, входящих в состав совокупности, обращается в верное равенство.

Возьмем неравенство x > 1 , x 2 ≥ 4 · x + 2 . Для него решением, например, будет тройка, т.к. она больше единицы, и, следовательно, она — верное решение для первого неравенства. А если мы возьмем ноль, то увидим, что ни к одному из неравенств он не подходит; значит, 0 в качестве решения совокупности мы рассматривать не можем , ведь запись вида 0 > 1 и x 2 ≥ 4 · x + 2 неверна.

Решение совокупности, в которую входит две, три и более переменных, — это две, три и более переменных, которые подходят в качестве решения хотя бы одному компоненту совокупности.

Возьмем еще один пример, посложнее. У нас есть совокупность:

x 2 + y 2 = 4 , x + y > 0 , x ≥ 3

Значения 3 и 0 будут верными решениями совокупности: они подходят в качестве верных значений в уравнения 2 и 3 ( 3 + 0 > 0 и 3 ≥ 3 — верно). А вот значения 2 и 1 не есть решение совокупности: ни к 1 , ни ко 2 , ни к 3 они не подойдут.

В некоторых учебниках можно встретить также понятия общего и частного решения совокупности; под частным при этом понимается одно решение, а под общим — их некое множество. Но более употребительно понятие просто решения совокупности, а о том, общее оно или частное, можно понять из контекста.

Также нужно отметить следующее: объединение решений всех компонентов совокупности также есть решение совокупности. Напомним, что решение системы представляет собой пересечение решений ее компонентов.

В продолжение темы мы советуем вам материал «Равносильные совокупности».

Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Решение совокупностей неравенств с одной переменной

Понятие совокупности неравенств с одной переменной и его решения

Несколько неравенств с одной переменной образуют совокупность , если нужно найти такое множество значений переменной, которое будет решением хотя бы одного из неравенств.

Решением совокупности неравенств с одной переменной является такое множество значений этой переменной, которое превращает хотя бы одно из неравенств в верное числовое неравенство.

Следствие: общим решением совокупности неравенств с одной переменной является объединение частных решений каждого из неравенств системы .

Например: $left[ begin x+7 ge 2 \ x-4 lt 1 end right. iff left[ begin x ge -5 \ x lt 5 end right. iff x in Bbb R$ — любое действительное число

Алгоритм решения системы неравенств с одной переменной

Шаг 1. Найти множество решений для каждого из неравенств системы. Если какое-либо частное решение является пустым множеством, отбросить его, но продолжить решение.

Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных непустых частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать.

Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их объединение – это и будет общим решением системы.

Шаг 4. Работа завершена.

Например: $left[ begin x-1 lt 0 \ x+5 ge 8 end right. iff left[ begin x lt 1 \ x ge 3 end right. iff x lt 1 cup x ge 3 или x in (-infty;1) cup [3;+infty) $

Сравнение систем и совокупностей неравенств

$left[ begin x+5 gt 3 \ x-7 lt 5 end right.$

$x gt -2 cap x lt 12 iff$

Объединение частных решений

$x gt -2 cap x lt 12 iff x in Bbb R$

Наличие одного частного решения $x in varnothing$

Вся система не имеет решений

$x in varnothing$

(аналогия с умножением на 0)

Вся совокупность может иметь

(аналогия с прибавлением 0)

Неравенства могут образовывать сложные конструкции условий из вложенных систем и совокупностей. Раскрытие скобок при упрощении таких конструкций подчиняется законам логики и правилам операций над множествами (см. §10 данного справочника).

Примеры

Пример 1. Решите совокупности уравнений:

$ а) left[ begin 5(x-1) ge 4(x+2) \ x lt 0 end right. iff left[ begin 5x-4x ge 8-5 \ x lt 0 end right. iff left[ begin x ge 3 \ x lt 0 end right. iff x lt 0 cup x ge 3 $

$x in (-infty;0) cup [3;+infty) $

$ б) left[ begin 2(x-5) gt x-11 \ x gt -3 end right. iff left[ begin 2x-x gt -11+10 \ x gt -3 end right. iff left[ begin x gt -1 \ x gt -3 end right. iff x gt -3 $

Пример 2. Решите неравенство:

Произведение слева будет отрицательным, если сомножители будут иметь разные знаки. Получаем совокупность двух систем неравенств:

$ left[ begin <left< begin x+3 gt 0 \ x-5 lt 0 end right.> \ <left< begin x+3 lt 0 \ x-5 gt 0end right.> end right. iff left[ begin <left< begin x gt -3 \ x lt 5 end right.> \ <left< begin x lt -3 \ x gt 5 end right.> end right. iff left[ begin -3 lt x lt 5 \ x in varnothing end right. iff -3 lt x lt 5 $

Произведение слева будет положительным (или равным 0), если сомножители будут иметь одинаковые знаки (или равными 0).

Получаем совокупность двух систем неравенств:

$ left[ begin <left< begin 2x+3 ge 0 \ 3x-2 ge 0 end right.> \ <left< begin 2x+3 le 0 \ 3x-2 le 0 end right.> end right. iff left[ begin <left< begin x ge -1,5 \ x ge frac end right.> \ <left< begin x le -1,5 \ x le frac end right.> end right. iff left[ begin x ge frac \ x le -1,5 end right. iff xle-1,5 cup xge frac $

$ x in (-infty;-1,5] cup [frac;+infty) $

Пример 3*. Решите неравенство: $(x^2+3x-4)(x^2+3x) lt 0$

Замена переменных: $ <left< begin x^2+3x = t \ (t-4)t lt 0 end right.>$

Для нижнего неравенства получаем совокупность:

$ left[ begin <left< begin t-4 gt 0 \ t lt 0 end right.> \ <left< begin t-4 lt 0 \ t gt 0end right.> end right. iff left[ begin <left< begin t gt 4 \ t lt 0 end right.> \ <left< begin t lt 4 \ t gt 0 end right.> end right. iff left[ begin t in varnothing \ 0 lt t lt 4 end right. iff 0 lt t lt 4 $

Возвращаемся к исходной переменной

$$ 0 lt x^2+3x lt 4 iff <left< begin x^2+3x gt 0 \ x^2+3x lt 4 end right.> iff <left< begin x^2+3x gt 0 \ x^2+3x-4 lt 0 end right.> iff <left< begin x(x+3) gt 0 \ (x+4)(x-1) lt 0 end right.> iff $$

$$ iff -4 lt x lt -3 cup 0 lt x lt 1 $$