ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
Гетерогенность дисперсных систем является причиной их оптической неоднородности и вызывает изменение направления световых, электронных, ионных и других лучей на межфазных поверхностях, а также неодинаковое поглощение или пропускание лучей веществами сопряженных фаз дисперсной системы. Всё это является причиной появления целого ряда специфических оптических явлений, присущих только коллоидным системам. Отличие оптических свойств коллоидных систем от свойств однородных сред привело к созданию целого ряда оптических методов исследования дисперсных систем, которые широко используются для изучения состава и структуры фаз, свойств межфазных поверхностей, дисперсности системы, а также природы, состава и структуры поверхностных слоёв.
Теоретические основы оптических явлений, характерных для дисперсных систем, и оптические методы их исследования следует изучить по учебникам, перечень которых приведен в списке литературы. В данном методическом пособии даётся только краткое теоретическое введение.
Основная часть издания посвящена практической части раздела «оптические свойства дисперсных систем» курса коллоидной химии и содержит подробное описание лабораторной работы по теме с практическими рекомендациями по её выполнению, обработке полученных данных и составлению отчета. Перед началом работы необходимо прочитать и принять к неукоснительному исполнению правила по технике безопасности, которые приведены в начале описания лабораторной работы и являются дополнением к общему инструктажу, проводимому со студентами в начале семестра.
Освоение практической части следует начинать только после изучения теории. Для теоретической подготовки по теме ниже приводится план теоретического коллоквиума. В конце методического пособия приведено приложение, которое является вспомогательным материалом, полезным для самоконтроля: контрольные вопросы и задачи.
ПЛАН ТЕОРЕТИЧЕСКОГО КОЛЛОКВИУМА
1. Общая характеристика оптических явлений.
2. Явление рассеяния света. Эффект Тиндаля. Влияние размеров частиц на вид индикатриссы рассеяния (диаграмма Ми).
3. Уравнение Рэлея и его анализ.
4. Светорассеяние токопроводящими сферическими частицами.
5. Абсорбция света. Уравнение Бугера – Ламберта — Бера. Оптическая плотность раствора, светопропускание, относительное поглощение.
6. Оптические методы исследования коллоидных систем: (принципиальные основы метода, его возможности и границы применимости):
а) световая и электронная микроскопия;
г) нефелометрия; определение молярной массы макромолекул.
7. Окраска коллоидных систем.
8. Лабораторная работа. Определение размеров частиц дисперсных систем турбидиметрическим методом:
a) Принципиальная оптическая схема фотоэлектроколориметра;
б) Определение размеров частиц дисперсных систем, подчиняющихся уравнению Рэлея;
в) Определение размеров частиц дисперсных систем, не подчиняющихся уравнению Рэлея, метод Геллера.
9. Самоподготовка по контрольным вопросам и задачам в приложении.
СПИСОК ЛИТЕРАТУРЫ
1. Фролов Ю.Г. Курс коллоидной химии. М., Химия, 1982г., с.245-267.
2. Боюцкий С.С. Курс коллоидной химии. М., Химия, 1975г., с. 33-53
3. Фридрихсберг Д.А. Курс коллоидной химии. Л., Химия, 1984г., с.38-44.
4. Лабораторные работы и задачи по коллоидной химии.- Под. ред. Ю.Г. Фролова и А.С. Гродского. М., Химия, 1986г., с.111-117.
5. Расчёты и задачи по коллоидной химии. Под ред. В.И.Барановой. М., Высш. шк., с. 254-260.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
РАССЕЯНИЕ СВЕТА, УРАВНЕНИЕ РЭЛЕЯ И ЕГО АНАЛИЗ
При падении луча света на дисперсную систему возможно его прохождение или преломление, а также отражение, рассеяние или поглощение света частицами дисперсной фазы. Прохождение света характерно для прозрачных гомогенных сред. Отражение – для микрогетерогенных и грубодисперсных систем с размерами частиц, превышающими длину волны падающего света (0,4 — 0,7 мкм), и проявляется в виде мутности суспензий, эмульсий и аэрозолей. Для коллоидных систем с радиусом частиц меньше длины волны падающего света характерны явления рассеяния света (опалесценция) и его поглощение (абсорбция).
Теория светорассеяния для сферических частиц, не проводящих электрический ток, разработана Рэлеем.
Дисперсные системы с размерами частиц, меньше длины световой волны, рассеивают свет во всех направлениях. При этом каждая точка неоднородности становится источником вторичных электромагнитных колебаний с частотой, равной частоте волны падающего света (дифракция). Частица представляет собой, таким образом, наведенный диполь, равный произведению поляризуемости частицы α на напряженность электрического поля Е:
Интенсивность рассеянного света определяется величинами, входящими в уравнение (1). Поляризуемость частицы α пропорциональна её объёму V, а интенсивность рассеяния света пропорциональна квадрату поляризуемости и, следовательно, квадрату объёма частицы. Таким образом, с ростом размера частиц интенсивность рассеяния возрастает. На поляризуемость влияет также разность показателей преломления дисперсной фазы n и дисперсионной среды n0.
Напряженность электрического поля Е характеризует плотность энергетического потока подающего света (его интенсивность) и пропорциональна квадрату амплитуды волны, излучаемой электрическим диполем (частицей дисперсной фазы). А поскольку амплитуда волны пропорциональна квадрату частоты колебаний диполя, то интенсивность рассеянного света Јр пропорциональна частоте колебаний диполя в четвертой степени или обратно пропорциональна длине волны λ в четвертой степени.
Если падающий свет не поляризован, то интенсивность рассеянного света зависит от направления распространения излучения: Јр пропорциональна (1+cos 2 Θ), где Θ – угол между направлениями падающего и рассеянного света ( угол рассеяния).
Таким образом, интенсивность рассеянного света различна в разных направлениях, при этом рассеянный свет частично поляризован. Рассеяние и поляризацию света частицей во всех направлениях характеризует векторная диаграмма Ми (рис.1). Стрелка указывает направление падающего луча. Незаштрихованная область соответствует интенсивности неполяризованного света, заштрихованная – поляризованной части.
Как видно из диаграммы, рассеянный свет не поляризован в направлении падающего луча и под углом 180 о . Максимально поляризован свет, рассеянный под углом 90 о к падающему лучу.
Теория Рэлея применима к разбавленным коллоидным растворам, поэтому возможность вторичного рассеяния не учитывается, и интенсивность рассеянного света пропорциональна числу частиц в единице объема, ν.
Уравнение Рэлея для интенсивности света Јр , рассеянного единицей объема дисперсной системы со сферическими частицами, не проводящими электрический ток, радиусом, значительно меньшим длины волны падающего света (r ≤ 0,1λ), на расстоянии R от частиц, в направлении, составляющем угол Θ с направлением падающего луча, имеет вид:
Jр= 
(2)
F = 
(3)
J0 – интенсивность падающего света;
ν — число частиц дисперсной фазы в единице объема (частичная концентрация);
и 
— соответственно, показатель преломления вещества дисперсной фазы и дисперсионной среды;
— объем одной частицы.
Рис.1. Диаграммы Ми, характеризующие рассеяние и поляризацию света сферическими частицами, не проводящими электрический ток:
а) малой; б) крупной частицей
Рассмотрим влияние различных параметров на интенсивность рассеянного света в соответствии с уравнением Рэлея.
1. Уравнение (2) применимо при отсутствии поглощения света, для «белых» неметаллических золей.
2. Область строгой применимости уравнения ограничена условием 
где r – радиус частиц дисперсной фазы. Для видимой части спектра 
это соответствует значениям радиуса r -6 см. Зависимость 
от r используется для определения размеров частиц дисперсных систем. Превышение указанных размеров частиц и приближение их к значениям 
приводит к снижению показателя степени при в уравнении Рэлея с 4 до 2,8. Нижняя граница показателя степени соответствует значениям r 
, когда явление рассеяния заменяется отражением света. Когда значение показателя степени при становится меньше 4, закон Рэлея перестает соблюдаться и для определения радиуса частиц пользуются эмпирическими методами. Наиболее распространен из них рассмотренный ниже метод Геллера.
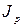
3. Зависимость интенсивности рассеянного света от концентрации частиц используется для определения концентрации (в отсутствие многократного рассеяния).
4. Согласно уравнению Рэлея, чем выше дисперсность частиц, тем меньше рассеяние. Приближение размеров частиц к молекулярным приводит к исчезновению опалесценции.
5. обратно пропорциональна λ 4 , т.е. при прохождении через коллоидный раствор пучка белого света рассеиваются в основном короткие волны, т.е. синяя область спектра. Это проявляется в голубоватой окраске коллоидных систем при боковом наблюдении. При рассмотрении кюветы с коллоидным раствором в проходящем свете, т.е. когда источник света по отношению к наблюдателю находится за кюветой, — раствор имеет оранжево – красные оттенки. Указанная закономерность объясняет применение синего цвета для светомаскировки и красного для сигнализации. Голубой цвет неба также объясняется опалесценцией, рассеиванием коротких волн солнечного излучения атмосферой Земли. При восходе и заходе солнца мы наблюдаем свет, прошедший через атмосферу, поэтому небо мы воспринимаем окрашенным в оранжево – красные тона.
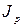
6. Разность показателей преломления частицы и среды весьма мала у растворов высокомолекулярных соединений и некоторых эмульсий. Светорассеяние для таких систем мало (в соответствии с уравнением (2)).
Видео:Химия | Дисперсные системыСкачать
2.4.6. Определение размера частиц в коллоидных системах оптическим методом
Оптический метод определения размера частиц в «белых» золях, т.е. коллоидных системах не поглощающих свет, основано на использовании уравнения Рэлея (2.2.103). Учитывая, что объемная доля частиц
j = n v1/ V = C /r, (2.2.112)
где n – число частиц в 1 см 3 золя или латекса;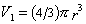 
– объем одной сферической частицы; С – массовая концентрация, г/см 3 ;r – плотность полимера, г/cм 3 ; r – радиус частиц, см.
Из уравнения Рэлея можем получить
, (2.2.113)
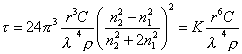
где t– мутность золя (латекса), которую можно измерить с помощью нефелометра, см — 1 ; l – длина волны падающего света, см; n1, n2 – коэффициенты преломления соответственно дисперсионной среды и дисперсной фазы,
. (2.2.114)
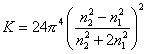
Уравнение (2.2.113) позволяет по измеренной мутности рассчитать радиус частиц, если система подчиняется закону Рэлея для рассеяния света, т.е. при r
Измерение мутности разбавленного белого золя проводят на нефелометре, а оптической плотности — на фотоколориметре. Иногда шкала фотоколориметра бывает отградуирована как в единицах мутности, так и в единицах оптической плотности.
Если радиус частиц больше l /20, то светорассеяние в таком золе не подчиняется уравнению Рэлея. Это выражается в том, что показатель степени при длине волны падающего света будет отличаться от 4.
Тогда используют эмпирическое уравнение Геллера
D = const l -a , (2.2.122)
или в логарифмической форме
lgD=lg (const) – a lgl . (2.2.123)
В уравнении (2.2.123) величина а обычно изменяется от 4 (рэлеевское рассеяние света) до 2 при r »l. Часто для белых золей используют параметр
где lср – среднее значение длин волн света, использованных для определения оптической плотности латекса.
Этот параметр зависит от показателя степени при длине волны использованного света a и после экспериментального определения последнего по углу зависимости, описываемой уравнением (2.2.123) находят по таблице величину Z и рассчитывают радиус частиц. Z лежит в пределах от 2 до 8.
Если Z 8 частицы уже видны в оптический микроскоп. Значения параметра Z и соответствующие ему показатели степени а при длине волны света приведены в табл. 2.1.
Рис. 2.18. Зависимость показателя степени при длине волны света в уравнении (2.2.122) от размера (радиуса) частиц в белых золях
Из табл. 2.1 видно, что постоянная а не может быть меньше 2,3 и больше 3,9.
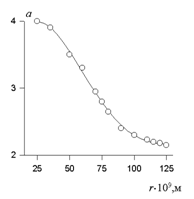
В 1946 г. Геллер установил зависимость показателя степени в уравнении (2.2.123) для белых золей от размера частиц, экспериментально определяемого независимым методом. Калибровочная кривая Геллера, которая может быть использована для графического определения радиуса частиц, приведена на рис. 2.18. Для радиуса частиц от 50 до 100 нм калибровочная зависимость имеет линейный вид и может быть описана уравнением
a = 3,1 — 2,16×10 -2 (r -50). (2.2.125)
Это уравнение справедливо для а = 3,1¸2,0. Для других значений показателя степени а расчет надо проводить с использованием функции Z. Для подавляющего большинства латексов синтетических полимеров радиус частиц более 25 нм, поэтому уравнение Рэлея не может быть использовано. Размер частиц таких латексов можно определить с помощью метода Геллера по результатам определения показателя степени при длине волны в уравнении (2.2.122) с последующим использованием табл. 2.1, калибровочной кривой или уравнения (2.2.125).
Видео:Оптические свойства дисперсных системСкачать
Оптические свойства. оптические свойства. Лабораторная работа «Оптические свойства дисперсных систем»
| Название | Лабораторная работа «Оптические свойства дисперсных систем» |
| Анкор | Оптические свойства |
| Дата | 18.12.2021 |
| Размер | 0.5 Mb. |
| Формат файла |  |
| Имя файла | оптические свойства.docx |
| Тип | Лабораторная работа #307835 |
Лабораторная работа «Оптические свойства дисперсных систем» Изучение оптических свойств дисперсных систем и методов их исследования; определение размеров частиц дисперсных систем и изучение кинетики образования гидрозоля. Оптические свойства дисперсных систем интересны тем, что интенсивность многих из них является максимальной в коллоидной области дисперсности. Эта особенность связана с тем, что длина световых волн видимой части спектра (400-760) 10 -9 нм сопоставима по всей величине с размерами коллоидных частиц. В основе оптических свойств высокодисперсных систем лежит два сложных световых явления – светорассеивание (опалесценция) и поглощение (абсорбция) света. Рассеяние света в грубодисперсных системах (обычных суспензиях и эмульсиях) обуславливается следующими тремя основными причинами: 1. отражением световых волн от наружных поверхностей частиц; 2. преломлением (в случае прозрачности дисперсной фазы); 3. полным внутренним отражением (также в случае прозрачности вещества частиц). Теория светорассеяния, разработанная Рэлеем, устанавливает зависимость интенсивности светорассеяния от внутренних и внешних факторов: где J 0 и J рас − интенсивности падающего и рассеянного света соответственно; F − функция показателей преломления; υ − концентрация частиц в единицу объема системы (частичная концентрация); Θ− угол между направлениями распространения рассеянного и падающего света. Уравнение Рэлея может быть использовано для определения размеров частиц сферической формы: если их радиус r не превышает 1/20 длины волны λ падающего света. Опытная проверка уравнения показала, что оно применимо для неметаллических частиц с размером от 5 до 100 ∙ 10 -9 м. С увеличением размеров частиц закон Рэлея перестает соблюдаться и интенсивность рассеянного света становится обратно пропорциональной длине волны в степени, меньшей, чем четвертая (для частиц с размерами (100 − 150) ∙ 10 -9 м – в третьей степени, для частиц с размерами (150 − 250) ∙ 10 -9 м – во второй степени). Для частиц еще больших размеров интенсивность рассеянного света перестает зависеть от длины волны падающего света. В этих случаях пользуются либо уравнениями, вытекающими из общей теории светорассеяния, либо эмпирическими соотношениями. Работа 2. Определение размеров частиц дисперсных систем, не подчиняющихся уравнению Рэлея Для получения гидрозоля серы используется окислительно-восстановительная реакция между гипосульфитом и соляной кислотой. В мерных колбах объемом 50 мл готовим отдельно водные растворы гипосульфата и соляной кислоты с концентрацией растворенных веществ от 0,1 н, затем равные объемы (10 мл) растворов соляной кислоты и гипосульфата смешиваем и наблюдаем за образованием гидрозоля (помутнением раствора). Удобнее и надежнее проводить эти наблюдения с помощью фотоэлектроколориметра. Для этого полученный раствор выливаем в кювету фотоэлектроколориметра и наблюдаем за изменениями оптической плотности. Через некоторое время показания перестали изменяться и образовалась дисперсная система с определенными размерами частиц дисперсной фазы. Значения оптической плотности D гидрозоля серы, измеренные на светофильтре с длиной волны 440 нм, должны находиться в пределах от 0,70 до 0,95. После приготовления золей определяем их оптическую плотность при различных длинах волн падающего света (в интервале 440-670 нм). При каждой длине волны оптическую плотность измеряем на фотоэлектроколориметре три раза и рассчитываем среднее значение Dср. Находим значения lgλ и lgDср. Строим график в координатах lgDср – lgλ Зависимость в соответствии с уравнением Геллера представляет собой прямую линию, тангенс угла наклона который равен показателю степени “n” с минусом. Значение показателя степени “n” в этих уравнениях зависит от соотношения между размером частицы и длиной волны падающего света, характеризуемого параметром “z”. Показатель “n” определяем по тангенсу угла наклона полученной прямой линии. По таблице принимаем Z=8,0. Тогда Найденные значения r соответствует среднему радиусу частиц гидрозоля. Экспериментальные данные для расчета размеров частиц дисперсных систем, не подчиняющихся уравнению Рэлея
Работа 3. Изучение кинетики образования гидрозоля В качестве объекта исследования используем гидрозоль серы. Его получаем на основе уравнения реакции между гипосульфитом и соляной кислотой, описанном выше (см. работу 2). Готовим в отдельных сосудах растворы гипосульфита и соляной кислоты 0,1 н. Затем равные объемы (10 мл) растворов соляной кислоты и гипосульфита быстро смешиваем и заливаем в кювету фотоэлектроколориметра. Включаем секундомер и через каждую минуту производим измерение интенсивности рассеянного света или оптическую плотность (светофильтр с λ = 440 нм). Строим график в координатах «оптическая плотность D – время t». На графике отмечаем индукционный период (tинд) реакции, соответствующий времени метастабильного состояния системы- стадии образования зародышей дисперсной фазы. 🔍 ВидеоХимия 11 класс (Урок№6 - Дисперсные системы.)Скачать  После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать  Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать  Лабораторная работа №8 Определение выталкивающей силы, действующей на погружённое в жидкость телоСкачать  Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать  Буферные системы, ацидоз и алкалоз, ур-ие Гендерсона-Гассельбаха (Атриум и Учим химию)Скачать  Система сходящихся сил. Решение задач по МещерскомуСкачать  Решение нелинейных системСкачать  Сопротивление материалов. Занятие 10. Часть 1. Расчет статически неопределимой балки.Скачать  Общее уравнение динамики. Расчет механической системы.Скачать  Системы показательных уравнений и неравенств. 10 - 11 классСкачать  Методы наблюдения и регистрации элементарных частиц | Физика 11 класс #45 | ИнфоурокСкачать  Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать  Расчет статически неопределимой стержневой системы. Уравнение совместимости деформацийСкачать  1 Решение задачи графическим и аналитическим методомСкачать  Принцип Даламбера. Определение реакций связей механической системы.Скачать  Урок 465. Методы регистрации элементарных частиц (часть 1)Скачать  ЛР-10-2-03 Определение коэффициента поверхностного натяжения методом отрыва капельСкачать  |
