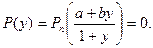Видео:🔴 Найдите корень уравнения (1/7)^(x-5)=49 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать
Отделение корней
Пусть дано уравнение вида (2.1), 
или (2.2),
Процесс численного решения уравнения разбивается на два этапа: отделение корней и уточнение корней.
Определение 2.2. Говорят, что корень Е, уравнения вида (2.1) или (2.2) отделен на данном промежутке, если он содержится в этом промежутке и других корней на том же промежутке нет.
Определение 2.3. Произвести полное отделение всех корней уравнения — значит разбить всю область допустимых значений на промежутки, в каждом из которых содержится только один корень или не содержится ни одного корня.
Для проверки существования корня уравнения на данном интервале применяют некоторые теоремы о свойствах непрерывных функций. Приведем некоторые из них.
Теорема 2.3 (первая теорема Больцано — Коши). Если функция/(х) непрерывна на отрезке [а; Ь] и принимает на концах отрезка значения разных знаков, то внутри отрезка [а; Ъ] существует, по крайней мере, один корень уравнения Дх) = 0.
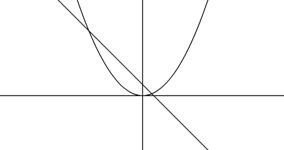
Рис. 2.5. К теореме 2.3
Заметим, что при выполнении условий теоремы 2.3 на отрезке [а; Ь] не следует, что на данном отрезке существует один или несколько корней (рис. 2.5). Важно иметь признак, по которому можно судить о наличии на отрезке [а; b] только одного корня. Этот признак выражается следующей теоремой (рис. 2.6).
Теорема 2.4. Если функция /(х) непрерывна и монотонна на отрезке [а; Ь] и принимает на концах отрезка значения разных знаков, то внутри отрезка [а; Ь] существует корень уравнения /(х) = 0, и притом единственный.
Рис. 2.6. К теореме 2.4
Вопрос о том, является ли функция монотонной, можно решить как элементарными методами, так и с помощью понятия производной, а именно: если функция Дх) непрерывна на отрезке [а; ?>] и имеет производную fix) внутри отрезка, то при fix) > 0 функция Дх) возрастает, а при/'(х) h(b), тогда внутри отрезка [а; Ь] существует корень уравнения g(x) = hix), и притом единственный.
Рис. 2.7. К теореме 2.6
Отделение корней лучше всего произвести графически. Для этого необходимо построить либо графики функций g(x) и h(x) для уравнения вида(2.1), либо график функцииДх) для уравнения вида (2.2). Построив соответствующие графики, можно сделать предположение о том, в каких интервалах находятся корни уравнения. Это предположение затем следует проверить аналитически, применяя одну из теорем 2.3—2.6.
Отделите корни уравнения х 3 — бх 2 + 20 = 0.
Построим график функцииу(х) = х 3 — бх 2 -I- 20 (рис. 2.8).
Рис. 2.8. Г рафик функции у(х) =х 3 — бх 2 + 20
На основе рис. 2.8 можно сделать предположение, что в каждом из отрезков [-2; -1], [2; 3], [5; 6] имеется по одному корню данного уравнения. Проверим это предположение для отрезка [2; 3]. На концах отрезка функция принимает значения
т.е. значения разных знаков. Производная
для всех х из интервала (2; 3), т.е. имеет постоянный знак. Следовательно, в силу теоремы 2.4 внутри отрезка [2; 3] уравнение х 3 — бх 2 + 20 = 0 имеет единственный корень.
Подобными рассуждениями можно доказать, что внутри каждого отрезка [-2; -1] и [5; 6] имеется по одному корню, в чем предлагаем убедиться читателю самостоятельно.
Видео:🔴 Найдите корень уравнения √(13-x)=3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать
Решение нелинейных уравнений
Пусть имеется нелинейное уравнение
Требуется найти корни этого уравнения, т. е. те значения х, которые обращают уравнение (3.1) в тождество. В процессе приближенного отыскания корней уравнения (3.1) обычно выделяют два этапа: отделение корня и уточнение корня.
Под отделением корня понимается определение промежутка, содержащего один и только один корень уравнения. Одна из точек этого промежутка принимается за начальное приближения корня. В зависимости от метода, который предполагается использовать для уточнения корня, требуется определение тех или иных свойств отделенного корня и поведение функции на отрезке отделения. Например, при использовании простейшего метода уточнения корня – метода дихотомии, необходимо и достаточно установить лишь непрерывность функции на отрезке отделения. При использовании других методов может потребоваться выяснить, является ли корень действительным, какова кратность корня, установить непрерывность и монотонность функции и ее некоторых низших производных.
В общем случае этап отделения корня уравнения (3.1) не может быть алгоритмизирован. Для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений) разработаны специальные приемы отделения корней, существенно облегчающие такое отделение и позволяющее автоматизировать этот процесс. Некоторые из этих приемов будут приведены при рассмотрении методов решений алгебраических уравнений. Нередко отделение корней нелинейных уравнений выполняется “вручную” с использованием всей возможной информации о функции f(x). В ряде случаев приближенное значение корня может быть определенно из физических соображений, если речь идет о решении нелинейного уравнения, связанного с конкретной прикладной задачей. Успешно применяется графический метод определения действительных корней, обладающей большой наглядностью и позволяющий относительно просто устанавливать возможность существования кратных корней. При графическом отделении корней бывает полезным представить уравнение (3.1) в эквивалентном виде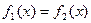 
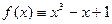
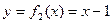
и искать точки пересечения функций 
и 
. Например, для уравнения 
вместо построения графика y = f(x) (рис. 3,а) проще построить графики функций 
и 
(рис.3,б).
В ряде случаев может быть полезной теорема, известная из курса математического анализа.
ТЕОРЕМА. Если функция f(x), определяющая уравнение f(x) = 0 , на концах отрезка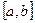 
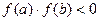
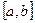
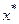
принимает значения разных знаков, т. е. 
, то на этом отрезке содержится по крайней мере один корень уравнения. Если же функция f(x) непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один корень 
уравнения.
Рисунок 3 – Графическое решение уравнения:
а) Пересечение исходной функции и оси абсцисс;
б) Пересечение двух упрощенных функций
В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.
Известно, что интервал, на котором расположены корни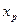 
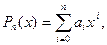
многочлена n-й степени 
в том числе и комплексные, выражается соотношением
.
Кроме того, по правилу знаков Декарта разность между числом перемен знаков последовательности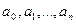 
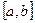
и числом положительных корней является либо положительным числом, либо нулем (в случае действительных корней). Это правило распространяется и на отрицательные корни при замене х на –х. Правило Декарта позволяет также оценить число действительных корней на интервале . Для этого обозначим 
и применим правило знаков к уравнению
Для отделения корня полезно также использовать теорему Гюа.
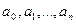
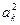
ТЕОРЕМА ГЮА. Если все корни алгебраического уравнения являются действительными числами, то для последовательности коэффициентов квадрат каждого некрайнего коэффициента больше произведения соседних с ним коэффициентов, т. е. 
> 
, k = 1, 2, …, n-1.
ТЕОРЕМА. Если для каких-либо k выполнено неравенство 
то многочлен имеет по крайней мере пару комплексных корней.
На втором этапе уточнения при нахождении корня используют два типа метода: ПРЯМЫЕ и ИТЕРАЦИОННЫЕ. В прямых методах корень уравнения может быть найден за конечное, заранее известное число операций. Прямыми методами удается решить некоторые простейшие алгебраические и тригонометрические уравнения.
В итерационных методах корень определяется как предел некоторой последовательности 
и решение не может быть достигнуто за конечное, заранее известное число операций.
Основные методы решения нелинейных уравнений и систем являются итерационными, и к их числу принадлежат метод дихотомии (половинного деления), метод простой итерации, метод Ньютона (метод касательных), метод секущих, метод парабол (метод Мюллера), метод Зейделя. Далее эти методы будут рассмотрены.
Важной характеристикой итерационных методов является скорость сходимости процесса. Говорят, что метод имеет n-й порядок сходимости, если 
, где С — постоянная, не зависящая от n. При n = 1 имеет место сходимость первого порядка, или линейная сходимость, а при n= 2 – второго порядка, или квадратичная. Говорят, что метод является одношаговым, если для построения итерационной последовательности нужно вычислить функцию в одной точке, двушаговым – в двух и т. п.
Сравнение различных методов следует проводить по числу операций при реализации одной итерации и по скорости сходимости.
Изложенные методы решения нелинейных уравнений и систем широко используются в численных методах оптимизации.
Видео:Как найти наибольший корень уравнения #shorts | ЕГЭ 2022 по математике | Эйджей из ВебиумаСкачать
3.1. Отделение корней нелинейного уравнения
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)
Верхняя граница положительных действительных корней 
определяется по формуле Лагранжа (Маклорена):
, (3.3)
Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней 
можно определить из вспомогательного уравнения
(3.4)
Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то
= 
(3.5)
Тогда все положительные корни многочлена лежат в интервале
≤x+≤
.
Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.
и 
.
≤x–≤ 
= 
=
.
Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3×8 – 5×7 – 6×3 – x – 9 = 0
K = 1 B = |– 9| an = 3
= 4
9×8 + x7 + 6×5 + 5x – 3 = 0
 |
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4
3×8 + 5×7 + 6×3 + x – 9 = 0
= 
9×8 – x7 – 6×5 – 5x – 3 = 0
K = 1 B = 6 an = 9
 |
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.
Рис. 3.1 Отделение корней на графике f(x).
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
На графике 2 корня.
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
📺 Видео
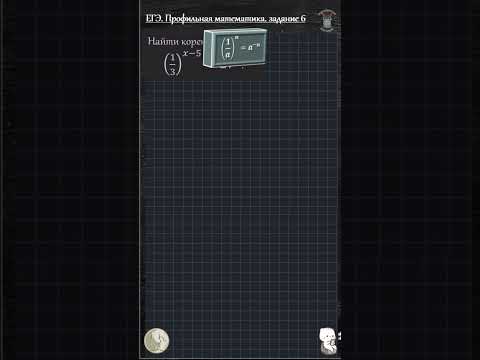
Найдите корень уравнения 3^(x-5)=81.Скачать
Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
СЛОЖИТЕ ДВА КОРНЯСкачать
ОГЭ, задание 9 #математика #огэСкачать
ЕГЭ. Математика, показательное уравненияСкачать
Как считать корни? #shortsСкачать
ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать
Уравнения с корнем. Иррациональные уравнения #shortsСкачать
Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать
ЕГЭ БАЗОВЫЙ УРОВЕНЬ НОМЕР 17 НАЙДИТЕ КОРЕНЬ УРАВНЕНИЯСкачать
8 класс. Алгебра. Решение уравнений, содержащих арифметические квадратные корни.Скачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Найдите корень уравненияСкачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
Неполные квадратные уравнения. Алгебра, 8 классСкачать
