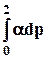В работах по химической термодинамике для формального описания зависимости химического потенциала реального газа от давления пользуются методом Льюиса (1901), согласно которому вводится новая функция f, которая называется фугитивностью или летучестью и имеет размерность давления:
(p, T) = (T) + RT ln f(p, T). (1.45)
Выражение (1.45) аналогично зависимости химического потенциала идеального газа от давления. Однако аналогия эта чисто формальна, поскольку фугитивность является функцией давления и температуры, причем характер зависимости f(p, T) индивидуален и зависит от природы газа. Коэффициентом фугитивности называется безразмерная величина
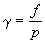
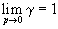
Из уравнений (1.43) и (1.45) вытекает:
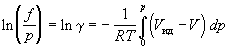
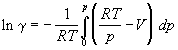
Используя определение фактора сжимаемости Z = pV/RT, уравнение (1.47) можно записать в виде:
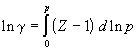
Используя уравнения (1.46) – (1.48), можно рассчитать фугитивность реальных газов графическими или аналитическими методами.
1.7.1. Графические методы
Графические методы используют для определения фугитивности чистого газа по экспериментальным данным об его объеме V при различных давлениях p и T = const.
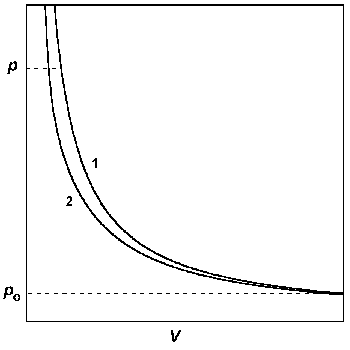
А) В координатах p – V строят изотермы идеального и реального газов от достаточно низкого давления, при котором эти изотермы практически сливаются, до давления, при котором требуется определить фугитивность. Интеграл в правой части уравнения (1.46) определяют графически (рис. 1.7).
Рис.1.7. Графический метод определения фугитивности: построение р — V изотерм для идеального (1) и реального (2) газов.
Б) Вычисляют объемную поправку реального газа , равную подынтегральному выражению в уравнениях (1.46) и (1.47):
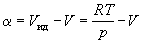
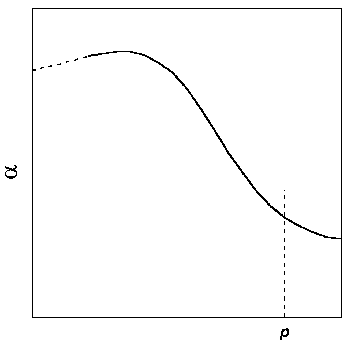
Затем строят зависимость от p при заданной температуре и интеграл в правой части уравнения (1.47) определяют графически(рис. 1.8).
Рис.1.8. Графический метод определения фугитивности: построение зависимости от р
Преимущества метода Б) по сравнению с методом А) заключаются в следующем. Во-первых, интервал изменения значительно меньше, чем V, особенно при высоких температурах. Во-вторых, при p 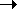
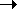
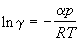
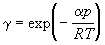
При низких p экспоненту можно разложить в ряд, ограничившись двумя членами:
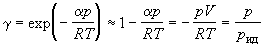
где pид – давление, которое имел бы идеальный газ, если бы он занимал тот же объем, что и реальный. С помощью уравнения (1.52) можно приближенно вычислять фугитивность при низких давлениях.
Смысл поправки при p 0 наглядно проявляется при использовании вириального уравнения состояния. При низких давлениях в уравнении (1.16) можно ограничиться членом со вторым вириальным коэффициентом, т.е.
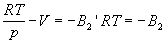
Таким образом, при p 0 поправка равна второму вириальному коэффициенту со знаком «минус». [Отметим, что при любых конечных значениях в пределе p 0 получается уравнение состояния идеального газа, поскольку RT – pV = p, и, следовательно, 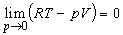
1.7.2. Аналитические методы
А). Аналитические методы основаны на подстановке в соотношение (1.47) уравнения состояния реального газа и аналитическом вычислении интеграла в правой части. Например, для газа Ван-дер-Ваальса после интегрирования получаем
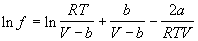
Точность расчета фугитивности будет определяться точностью используемого уравнения состояния в исследуемом интервале p и T.
Б). Фугитивность газа можно приближенно определить на основе закона соответственных состояний (метод Ньютона). Согласно закону соответственных состояний, коэффициент фугитивности является универсальной функцией приведенных давления pr и температуры Tr. Зависимость ( pr, Tr) представляют в виде обобщенных диаграмм или уравнений, из которых легко определить коэффициент фугитивности (и фугитивность f = p), зная критические параметры газа.
Задачи и упражнения к главе 1
* Задачи, помеченные звездочкой, рекомендуется решать с помощью компьютера, оснащенного программой графической обработки экспериментальных данных, например, Excel, Origin или SigmaPlot.
1.1. Выразите уравнение состояния Ван-дер-Ваальса в виде вириального разложения по степеням 1/Vm и получите выражения для вириальных коэффициентов B2 и B3 через параметры a и b. Воспользуйтесь разложением: 1/(1–x) = 1 + x + x 2 + .
1.2. Уравнения (1.15) и (1.16) являются разложениями по степеням 1/Vm и p, соответственно. Найдите соотношение между B2, B3 и B2‘, B3‘.
1.3. Предложено следующее уравнение состояния:
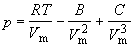
Покажите, что это уравнение приводит к критическому поведению. Выразите критические константы газа через параметры B и C и получите выражение для фактора сжимаемости в критической точке.
1.4. Покажите, что для газа с жесткими молекулами сферической формы при учете только парных взаимодействий константа b в уравнении Ван-дер-Ваальса равна учетверенному собственному мольному объему молекул. Оцените значение b для Ne, если его молекулярный диаметр равен 0.258 нм.
1.5.* Покажите, что второй вириальный коэффициент и молярную массу газа можно получить, строя график p/ от p, где p – давление газа, – его плотность. Рассчитайте B2 для диметилового эфира, пользуясь следующими данными:
| р,Торр | 91,74 | 188,98 | 277,3 | 452,8 | 639,3 | 760,0 |
| ,г/л | 0,232 | 0,489 | 0,733 | 1,25 | 1,87 | 2,30 |
1.6.* Рассчитайте второй вириальный коэффициент для водорода при 0° C, пользуясь следующими данными:
| р, бар | 50,7 | 101,3 | 202,6 | 303,9 |
| V,л/моль | 0,4634 | 0,2386 | 0,1271 | 0,090 |
1.7.* Пользуясь правилом прямолинейного диаметра [уравнение (1.2)], определите критический мольный объем CCl4, используя следующие данные:
| t, o C | 100 | 150 | 200 | 250 | 270 | 280 |
| ж,г/см 3 | 1,4343 | 1,321 | 1,1888 | 0,9980 | 0,8666 | 0,7634 |
| п, г/см 3 | 0,0103 | 0,0304 | 0,0742 | 0,1754 | 0,2710 | 0,3597 |
Критическая температура CCl4 равна 283,1 o C.
1.8. Найдите 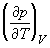
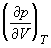
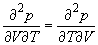
1.9. Выведите выражение для работы изотермического обратимого расширения газа, подчиняющегося уравнению состояния Ван-дер-Ваальса.
1.10. Выведите выражение для работы изотермического обратимого расширения газа, подчиняющегося вириальному уравнению состояния (1.15).
1.11. Второй и третий вириальные коэффициенты в уравнении (1.15) для аргона при 273 К равны соответственно В2 = – 21,7 см 3 /моль и В3 = 1200 см 6 /моль 2 . Рассчитайте: а) работу обратимого изотермического расширения при этой температуре, б) работу расширения против постоянного давления 1 атм и в) работу расширения в предположении, что аргон ведет себя идеально. Примите, что Vm,1 = 500 см 3 и Vm,2 = 1000 см 3 .
1.12. Покажите, что работа изотермического обратимого расширения газа Ван-дер-Ваальса может быть выражена в виде приведенных переменных и что, определив приведенную работу как Ar = A3b/a, можно получить выражение, не зависящее от природы газа.
Литература к главе 1
1.М.П. Вукалович, И.И. Новиков
Уравнение состояния реальных газов
М.-Л., Госэнергоиздат, 1948.
2.В.И. Горшков, И.А. Кузнецов
Основы физической химии
М.: Изд-во Моск. ун-та, 1993.
3.Физическая химия / под ред. Б.П. Никольского
Л.: Химия, 1987.
4.Курс физической химии / под ред. Я.И. Герасимова. Т. 1
М.: Госхимиздат, 1963.
5.Е.Н. Еремин.
Основы химической термодинамики
М.: Высшая школа, 1978.
6.Е.М. Кузнецова, Е.П. Агеев
Термодинамика в вопросах и ответах
М.: Химический факультет МГУ, 1997.
7.Э. Мейсон, Е. Сперлинг
Вириальное уравнение состояния
М.: Мир, 1972
8.О.М. Полторак
Термодинамика в физической химии
М.: Высшая школа, 1991.
9.R.A. Alberty, R.J. Silbey
Physical Chemistry
Wiley, New York, 1997.
10.P.W. Atkins
Physical Chemistry
Oxford University Press, 1994.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Видео:ФИЗИЧЕСКАЯ ХИМИЯ (ТЕРМОДИНАМИКА). ОСНОВНЫЕ ПОНЯТИЯ: СИСТЕМЫ, ПАРАМЕТРЫ, ФУНКЦИИСкачать

Способ определения летучести и теплоты испарения смеси жидких веществ
Владельцы патента RU 2488811:
Изобретение относится к области исследования или анализа небиологических материалов путем определения их химических или физических свойств, конкретно, исследования фазовых изменений путем удаления какого-либо компонента, например, испарением, и взвешивания остатка. Способ определения летучести и теплоты испарения смеси жидких веществ по скорости испарения с плоской поверхности заключается в том, что устанавливают корреляционную зависимость значений летучести, рассчитываемых по известным справочным данным, для индивидуальных жидких веществ, выбранных в качестве градуировочных жидкостей, от скорости их испарения, определяемой на основании данных термогравиметрического анализа, осуществляемого в изотермическом режиме при достижении равновесного состояния. При этом для исследуемой смеси определяют скорость испарения и по корреляционной зависимости находят значение летучести. Затем, используя зависимость найденных значений летучести от температуры, определяют теплоту испарения смеси жидких веществ в исследуемом интервале температур. Причем величину теплоты испарения смеси определяют по величине тангенса угла наклона графика прямолинейной зависимости, абсциссой которого является величина обратной абсолютной температуры, а ординатой — логарифм произведения экспериментально найденного значения летучести на величину абсолютной температуры. Техническим результатом изобретения является повышение достоверности и объективности оценки летучести не только индивидуальных жидкостей, но и их смесей при различных температурах, расширении функциональных возможностей способа определения летучести. 1 з.п. ф-лы, 4 табл., 6 ил.
Изобретение относится к области исследования или анализа небиологических материалов путем определения их химических или физических свойств, конкретно, исследования фазовых изменений путем удаления какого-либо компонента, например, испарением, и взвешивания остатка.
Летучесть — свойство жидких и твердых веществ переходить в газообразное состояние. Мерой летучести является концентрация насыщенного пара данного вещества при рассматриваемой температуре. Летучесть выражается в мг/м 3 или в мг/л и рассчитывается по выражению (1):
C = P ⋅ M / R ⋅ T , ( 1 )
где C — концентрация насыщенного пара;
P — давление газа;
M — молекулярная масса газа;
R — универсальная газовая постоянная;
T — абсолютная температура.
Выражение (1) является следствием уравнения состояния идеальных газов (уравнение Клапейрона-Менделеева):
P ⋅ V = n ⋅ R ⋅ T , ( 2 )
где V — объем газа при температуре T;
n — число молей исследуемого газа.
Учитывая, что n=m/M, где m — масса газа, и, сделав математические преобразования уравнения (2), получаем выражение для расчета летучести (1).
С повышением температуры увеличивается давление насыщенного пара вещества, выражение (2), вследствие чего возрастает и его летучесть /Химический энциклопедический словарь [Текст] / М.: Советская энциклопедия, 1983. — 792./.
Известны прямые и косвенные методы определения летучести индивидуальных веществ. Для определения давления насыщенного пара и летучести прямыми методами необходимо достичь насыщения воздуха парами исследуемого вещества. Насыщение воздуха парами вещества может быть только в статических условиях закрытого объема /Хала Э. Равновесие между жидкостью и паром [Текст] / Э.Хала, И.Пик, В.Фрид [и др.]. — М.: ИЛ, 1962. — 438 с.; Рид Р. Свойства газов и жидкостей [Текст]: пер. с англ. / Р.Рид, Дж.Праусниц, Шервуд. — Л: Химия, 1982. — 591 с./.
Косвенные методы определения давления насыщенного пара и летучести основаны на использовании соотношений хроматографических параметров удерживания исследуемого вещества и вещества сравнения, для которого известны справочные данные по летучести /Головни Г.В. Определение летучести гербицидов производных 2,4-Д методом газожидкостной хроматографии [Текст] / Г.В.Головин, В.Ф.Снегирев, М.М.Атурян [и др.] // Химия в сельском хозяйстве. — 1974. — №4. — стр. 67-71; Туркельтауб Г.Н. Определение упругости пара на серийном хроматографическом приборе [Текст] / Г.Н.Туркельтауб, Б.М.Лускина // Заводская лаборатория. — 1969. — №10. — с.1193; А.с. 800868 СССР МКИ 3 G01N 31/08. Способ определения давления насыщенного пара легкоконденсирующейся примеси в неконденсируемой газовой смеси [Текст] / В.Г.Сагайдак, С.С.Петухов, А.И.Туманов (СССР). — 1976 г./.
Несмотря на многообразие известных методов определения максимальной концентрации насыщенных паров в воздухе, все они касаются индивидуальных соединений, но не их смесей. Возможно прямое определение давления насыщенного пара смеси органических соединений в замкнутом объеме, однако для расчета максимальной концентрации паров по выражению (1) необходимы данные о молекулярной массе смеси, расчет которой для смеси сложного, а порой неопределенного, состава является проблематичным.
В связи с этим исследования по разработке способа определения летучести смесей жидких органических веществ можно признать актуальными.
Известно, что летучесть определяет скорость испарения исследуемого вещества с плоской поверхности /Кузнецов В.В. Физическая и коллоидная химия [Текст] / В.В.Кузнецов. — 2-е изд. — М: Высшая школа, 1968. — 390 с.; Франке З. Химия отравляющих веществ [Текст]: В 2 т. / З.Франке. — М.: Химия, 1973. — Т.1. — 365 с./.
На взаимосвязи скорости испарения с плоской поверхности и летучести основан известный способ определения относительной летучести растворителей по этиловому эфиру /ГОСТ 18188-72, п.3.4. Растворители марок 645, 646, 647, 648 для лакокрасочных материалов. Технические условия [Текст]. — М: ИПК Изд-во стандартов, 1972./. В этом способе летучесть растворителей оценивается относительно летучести этилового эфира, характеризуемой временем полного испарения пятна жидкости, нанесенного на плоскую поверхность беззольного фильтра, то есть фактически скоростью испарения.
Данный способ является ближайшим из аналогов. При несомненных достоинствах этого способа он обладает и рядом недостатков:
— не предполагает определения абсолютных значений летучести;
— не позволяет оценить зависимость летучести исследуемой жидкости от температуры;
— субъективность оценки полноты испарения нанесенного пятна жидкости не предполагает высокой точности определения относительной летучести.
Задача настоящего изобретения заключается в разработке способа определения абсолютных значений летучести при различных температурах и теплоты испарения смеси жидких веществ.
Решение поставленной задачи предполагает технический результат, заключающийся в повышении достоверности и объективности оценки летучести не только индивидуальных жидкостей, но и их смесей при различных температурах, расширении функциональных возможностей способа определения летучести за счет возможности использования полученных экспериментальных данных для определения теплоты испарения.
Заявляемый способ может быть использован на стадии разработки новых жидких смесевых систем лакокрасочных и горюче-смазочных материалов при оценке их физико-химических свойств, показателей взрывоопасности и пожароопасности и при оптимизации состава.
Поставленная задача решается тем, что в способе определения летучести и теплоты испарения смеси жидких веществ по скорости испарения с плоской поверхности согласно предлагаемому решению устанавливают корреляционную зависимость значений летучести, рассчитанных по известным справочным данным для индивидуальных жидких веществ, выбранных в качестве градуировочных жидкостей, от скорости их испарения, определяемой на основании экспериментальных данных термогравиметрического анализа, осуществляемого в изотермическом режиме при достижении равновесного состояния; для исследуемой смеси определяют скорость испарения и по корреляционной зависимости находят значение летучести; затем, используя зависимость найденных значений летучести от температуры, определяют теплоту испарения смеси жидких веществ в исследуемом интервале температур.
Величину теплоты испарения смеси определяют по величине тангенса угла наклона, графика прямолинейной зависимости, абсциссой которого является величина обратной абсолютной температуры, а ординатой — логарифм произведения экспериментально найденного значения летучести на величину абсолютной температуры.
Предлагаемое изобретение поясняется рисунками, представленными на фигурах 1-6. На первом этапе исследований по разработке способа определения летучести и теплоты испарения смеси жидких веществ был обоснован выбор соединений, пригодных для построения корреляционной (градуировочной) зависимости при оценке летучести исследуемых смесей жидких веществ.
При решении задачи по обоснованию выбора соединений, пригодных для построения градуировочной зависимости при оценке летучести исследуемых смесей жидких веществ, были рассчитаны величины давления и концентрации насыщенного пара при температуре 20°С для представителей гомологических рядов предельных и ароматических углеводородов, спиртов.
При этом использовались таблицы справочных данных по температуре и давлению насыщенных паров /Стэлл Д.Р. Таблицы давления паров индивидуальных веществ [Текст]: справочник / Д.Р.Стэлл. — М., Иностранная литература, 1949. — 72 с./. Для расчета давления и концентрации насыщенного пара при заданной температуре использовали упрощенное уравнение Клапейрона (3) /Пригожий И. Химическая термодинамика [Текст] / И.Пригожин, Р.Дефэй — Новосибирск.: Наука, 1966. — 550 с./ и выражение (4) для расчета концентрации насыщенного пара как следствие выражения (1):
ln P = A − B / T , ( 3 )
где P — давление насыщенных паров;
T — абсолютная температура парожидкостной системы;
A, B — коэффициенты.
C = 15,9 ⋅ P ⋅ M / T , ( 4 )
где C — летучесть (концентрация насыщенного пара), мг/л;
15,9 — коэффициент, учитывающий значение универсальной газовой постоянной R и соотношение единиц /Вигдергауз М.С. Расчеты в газовой хроматографии [Текст] / М.С.Вигдергауз. — М: Химия, 1978. — 248 с./;
P — давление насыщенного пара, мм рт.ст.;
M — молекулярная масса, г/моль;
T — температура, K.
Уравнение (3) является математическим выражением линейной зависимости ln P от 1/T, причем коэффициент B (тангенс угла наклона прямой) связан с теплотой испарения: B=ΔH/R, откуда следует, что:
Δ H = B ⋅ R , ( 5 )
где B — коэффициент уравнения (3),
ΔH — мольная энтальпия парообразования (теплота испарения), кал/моль;
R — универсальная газовая постоянная, равная 1,98 кал/моль·K.
Несмотря на то, что в соответствии с выражением (4) концентрация насыщенного пара прямо пропорциональна молекулярной массе и давлению, летучесть уменьшается с возрастанием молекулярной массы, поскольку при этом уменьшается и давление насыщенного пара. Максимальной летучестью обладают первые члены гомологических рядов, при этом зависимость теплоты испарения от количества атомов углерода в молекуле гомологов имеет линейный характер.
Исходя из этого, нами были выбраны в качестве соединения с максимальной летучестью пентан или диэтиловый эфир. В качестве соединений с промежуточными значениями летучести при построении градуировочной зависимости можно выбрать жидкости, представители различных классов органических соединений: воду, бензол, ацетон, метиловый спирт. Однако перечень выбранных соединений требует уточнения с учетом возможностей методики определения скорости испарения.
Определение скорости испарения жидкости основано на измерении убыли массы испаряемого вещества за известный промежуток времени. Для этого используется гравиметрический метод. При несомненных достоинствах и универсальности этого метода реальная осуществимость его зависит, в первую очередь, от точности взвешивания образца; кроме того, от точности измерения промежутка времени и от точности термостатирования при определении скорости испарения.
Сочетание высокой точности взвешивания и термостатирования при проведении эксперимента по определению скорости испарения может быть достигнуто при использовании термогравиметрического метода.
Экспериментально-теоретические исследования, направленные на разработку методики определения скорости испарения индивидуальных компонентов и исследуемых смесей жидких веществ, их летучести с использованием термогравиметрического метода анализа, способствуют расширению функциональных возможностей метода.
Трудность решения задачи по разработке методики определения скорости испарения связана с тем, что используемое стандартное оборудование для термогравиметрических исследований (термоанализатор DTG-60 фирмы Shimadzu, Япония) не позволяет проводить исследования в изотермическом режиме. Поэтому образец подвергался кратковременному прогреву в открытых платиновых ячейках в атмосфере воздуха со скоростью 2…10°/мин до равновесной температуры в диапазоне 20…60°С. Точность измерения массы — 1%, чувствительность — 0,005 мг. Точность измерения температуры — 0,1°С.
При испарении с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает кинетическую энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, то есть к охлаждению жидкости. В результате процессов нагревания и испарения образца устанавливается состояние равновесия, при этом изменения температуры не превышали 0,1°. Температура, соответствующая такому состоянию, фиксировалась в качестве температуры определения скорости испарения. На фигуре 1 приведены в состоянии наложения термограммы для определении скорости испарения воды.
Кривые стабилизации температуры (1, 2, 3) на фигуре 1 отражают температуры установления равновесного состояния: 17,8; 43,9 и 47,4°С. Для каждой из этих температур на фигуре 1 представлены кривые термогравиметрического анализа (ТГА) (4, 6, 8) и дифференциального термического анализа (ДТА) (5, 7, 9) воды.
Диапазон стабилизации температуры с точностью до 0,1°С позволяет выделить на кривой ТГА прямолинейный участок, соответствующий убыли массы при испарении жидкости, который следует использовать при определении скорости испарения.
На начальном этапе экспериментальных исследований было обнаружено, что ранее обоснованный перечень жидкостей для построения градуировочной зависимости летучести от скорости испарения должен быть откорректирован. Так, определение скорости испарения глицерина возможно при температурах более 60°С, поскольку при более низких температурах наблюдается не убыль массы образца, а ее увеличение: процесс абсорбции влаги воздуха преобладает над процессом испарения малолетучей жидкости.
Использование пентана или диэтилового эфира в качестве образцов с максимальной летучестью ограничено техническими возможностями определения высоких скоростей испарения, поскольку требует захолаживания образцов. Поэтому в качестве соединений для построения градуировочной зависимости были использованы следующие соединения: вода, метиловый спирт, бензол и ацетон.
Однако экспериментальные данные, в частности для воды, позволяют определять скорость испарения при конкретных температурах равновесного состояния (17,8; 43,9 и 47,4°С). При определении скорости испарения для любой требуемой температуры, необходима зависимость скорости испарения от температуры. Для установления такой зависимости можно использовать математический аппарат исследования кинетики химических процессов.
Расчеты кинетических параметров по кривой ТГА основаны на формальном кинетическом уравнении:
V = − d m / d τ = K ⋅ m n , ( 6 )
где V — скорость реакции;
m — масса непрореагировавшего вещества в момент времени τ;
n — порядок реакции;
K — константа скорости реакции.
Исследуемый процесс испарения не является химическим процессом, поэтому, применяя кинетические уравнения, имеет смысл вести речь об изменении массы вещества за счет превращения в пар, но без химического превращения в другое соединение.
В случае, когда зависимость изменения массы от времени имеет линейный характер как при исследовании процесса испарения, а тангенс угла наклона является величиной постоянной, не зависящей от массы, порядок реакции равен нулю. Для реакции нулевого порядка скорость реакции численно равна константе скорости:
d m / d τ = − K . ( 7 )
При этом для узкого интервала температур справедливо уравнение Аррениуса, отражающее зависимость константы скорости от температуры:
K = K o ⋅ e − E / R T , ( 8 )
где K — константа скорости реакции при температуре T;
Ko — постоянный коэффициент температурной зависимости;
E — энергия активации реакции;
R — универсальная газовая постоянная.
С учетом выражения (7) зависимость скорости испарения от температуры имеет такой же характер. В логарифмической форме зависимость скорости испарения от температуры имеет вид:
ln V и с п = A 1 − B 1 ⋅ 1 / T , ( 9 )
где Vисп — скорость испарения при температуре t, °С;
T — абсолютная температура, (t+273), K;
E = B 1 ⋅ R . ( 10 )
На фигуре 2 приведены зависимости логарифма экспериментально найденных значений скорости испарения исследуемых жидкостей от величины обратной абсолютной температуры.
Как видно на фигуре 2, приведенные зависимости носят линейный характер с коэффициентом корреляции, r 2 , не менее 0,98, что является подтверждением того, что процесс испарения описывается кинетическим уравнением нулевого порядка. Это позволяет использовать их в расчете скорости испарения для любой температуры в диапазоне проводимых исследований 10…40°С.
В таблице 1 приведены результаты расчета скорости испарения исследуемых жидкостей по экспериментально найденным зависимостям, фигура 2, для выбранных значений температуры: 10, 20, 30, 40°С. В этой же таблице приведены значения давления насыщенного пара и летучести, рассчитанные с использованием выражений (3, 4) для температуры: 10, 20, 30, 40°С.
Подтверждением корреляции значений летучести и скорости испарения является зависимость, представленная на фигуре 3 на основании данных таблицы 1 для интервала температур 10…40°С.
Поскольку значения максимальной концентрации насыщенных паров являются расчетными величинами, а значения скорости испарения определены экспериментально, наличие прямолинейной зависимости для всех четырех соединений с коэффициентом корреляции, r 2 , не менее 0,99 подтверждает объективность предположения о возможности оценки летучести по скорости испарения.
Используя данные таблицы 1, можно построить графики корреляционных (градуировочных) зависимостей летучести от скорости испарения для воды, метанола, бензола и ацетона как веществ, выбранных в качестве градуировочных соединений, при температурах 10, 20, 30 и 40°С. На фигуре 4 приведена корреляционная (градуировочная) зависимость летучести от скорости испарения для температуры 20°С.
| Таблица 1 | |||||
| Результаты расчета скорости испарения, давления насыщенного пара и летучести исследуемых жидкостей | |||||
| Название соединения | Определяемая характеристика | Значения определяемой характеристики при температуре, °С | |||
| 10 | 20 | 30 | 40 | ||
| Вода | Скорость испарения, Vисп, мг/мин | 0,18 | 0,31 | 0,53 | 0,91 |
| Энергия активации, Eэксп, ккал/моль | 9,6 | ||||
| Давление насыщенного пара, P, мм рт.ст. | 9,0 | 18,0 | 34,1 | 64,1 | |
| Летучесть, Cmax, мг/л | 9,1 | 17,6 | 32,2 | 53,6 | |
| Метанол | Скорость испарения, Vисп, мг/мин | 0,30 | 0,61 | 1,17 | 2,24 |
| Энергия активации, Еэксп, ккал/моль | 11,7 | ||||
| Давление насыщенного пара, P, мм рт.ст. | 54,1 | 94,8 | 159,2 | 266,1 | |
| Летучесть, Cmax, мг/л | 97,2 | 164,3 | 267,3 | 430,9 | |
| Бензол | Скорость испарения, Vисп, мг/мин | 1,48 | 2,22 | 3,22 | 4,64 |
| Энергия активации, Eэксп, ккал/моль | 6.7 | ||||
| Давление насыщенного пара, P, мм рт.ст. | 37,0 | 65,1 | 108,9 | 182,2 | |
| Летучесть, Cmax, мг/л | 162,0 | 273,9 | 445,5 | 722,1 | |
| Ацетон | Скорость испарения, Vисп, мг/мин | 2,10 | 3,72 | 6,30 | 10,59 |
| Энергия активации, Eэксп, ккал/моль | 9.5 | ||||
| Давление насыщенного пара, P, мм рт.ст. | 110,0 | 177,3 | 275,9 | 428,4 | |
| Летучесть, Cmax, мг/л | 358,3 | 559,2 | 840,0 | 1262,2 |
Как видно на фигуре 4, корреляционная зависимость имеет линейный характер с коэффициентом корреляции, r 2 , равным 0,94, и позволяет рассчитывать летучесть смеси по экспериментальным данным скорости испарения при температуре 20°С. Зависимости для других температур также имеют линейный или близкий к линейному характер, следовательно, могут быть использованы в качестве градуировочных зависимостей при оценке летучести смесей при различных температурах.
Следующий этап исследований был посвящен определению теплоты испарения для смесей жидкостей по экспериментальным значениям летучести.
Для индивидуальных веществ и искусственных смесей известного состава можно рассчитать молекулярную массу смеси и определить давление насыщенного пара при различных температурах, а, имея зависимость давления насыщенного пара от температуры, оценить теплоту испарения смеси, используя выражение (5).
Однако для реальных смесей сложного состава определение молекулярной массы смеси может оказаться сложной и непродуктивной работой, поскольку для этого необходимо провести качественный и количественный анализ смеси по всем ее компонентам. Без величины молекулярной массы смеси невозможно рассчитать давление насыщенного пара, а следовательно, и определить теплоту испарения.
Несложными математическими преобразованиями выражений (3, 4) можно показать, что зависимость логарифма произведения летучести на абсолютную температуру от величины обратной абсолютной температуры выражается уравнением прямой линии как и зависимость логарифма давления, выражение (3). Причем значение второго коэффициента В уравнения прямой, связанного с величиной теплоты испарения, одинаково в обоих случаях:
ln ( C ⋅ T ) = ( ln 15,9 M + A ) − B ⋅ 1 / T , ( 11 )
где C — летучесть жидкости при абсолютной температуре T;
M — молекулярная масса;
A, B — коэффициенты линейного уравнения.
Данное выражение позволяет определять теплоту испарения для смесей по экспериментальным значениям летучести. На фигуре 5 приведены графики зависимостей (3) и (11) для искусственной смеси метанола с водой в объемном соотношении 1:1.
Как видно на фигуре 5, прямые параллельны, то есть имеют одинаковый тангенс угла наклона, одинаковый коэффициент B уравнения прямой, а, следовательно, одинаковые значения теплоты испарения.
Уравнения прямых, приведенных на фигуре 5, имеют вид:
lnP=22,04-5418·1/T, r 2 =0,99;
ln(C·Т)=28,01-5445·1/Т, r 2 =0,99.
Значения коэффициента B уравнений различаются между собой не более, чем на 0,5%.
Следовательно, можно по экспериментально определенным значениям летучести оценить теплоту испарения смеси жидкостей, не имея данных по молекулярной массе и давлению насыщенного пара.
Пример осуществления способа
При проверке возможности использования корреляционных (градуировочных) зависимостей для оценки летучести смеси были приготовлены двухкомпонентные смеси метанола с водой с объемным соотношением метанола к воде 1:1, 2:1 и 1:2. Выбор компонентов смеси обусловлен тем, что наличие данных по давлению насыщенного пара и летучести исходных компонентов смеси позволит проверить правильность оценки летучести смеси, используя результаты расчетов на основании закона Рауля /Химический энциклопедический словарь [Текст] / М: Советская энциклопедия, 1983. — 792/:
P = P o ⋅ X , ( 12 )
где P — давление насыщенного пара растворителя над раствором;
P o — давление насыщенного пара чистого растворителя при данной температуре;
X — мольная доля растворителя в растворе.
Частным случаем применения закона Рауля для смеси взаимно смешивающихся жидкостей является выражение:
P = ∑ ( P i o ⋅ μ i ) , ( 13 )
где P — давление насыщенного пара смеси;
P i o 
µi — мольная доля i-того компонента смеси в жидком состоянии.
На фигуре 6 приведены зависимости логарифма экспериментальных значений скорости испарения исследуемых двухкомпонентных смесей метанола с водой от величины обратной абсолютной температуры.
В таблице 2 приведены результаты расчета скорости испарения для смесей метанола с водой по экспериментально определенным зависимостям, фигура 6, для выбранных значений температуры: 10, 20, 30, 40°С. В этой же таблице приведены значения молекулярной массы смеси, рассчитанные по выражению (14), и экспериментальные значения энергии активации процесса испарения, найденные по выражению (10), используя тангенс угла наклона прямых (фигура 5), в сравнении с расчетными величинами энергии активации, выражение (15).
Анализ данных, приведенных на фигуре 6, позволяет сделать вывод о том, что и для смесей зависимости логарифма скорости испарения от величины обратной абсолютной температуры имеют линейный характер с коэффициентом корреляции, r 2 , не менее 0,97, что является подтверждением того, что процесс испарения описывается кинетическим уравнением нулевого порядка. Эго позволило использовать их для расчета скорости испарения для любой температуры в диапазоне проводимых исследований 10…40°С (таблица 2). При этом значения энергии активации для смеси, найденные экспериментальным путем, близки к расчетным значениям.
| Таблица 2 | ||||||||
| Результаты расчета молекулярной массы, скорости испарения и энергии активации процесса испарения для смесей метанола с водой | ||||||||
| Объемное соотношение метанола и воды | Мольная доля метанола в смеси, µ1 | Молекулярная масса, M, г/моль | Скорость испарения, Vисп, мг/мин, при температуре, t, °С | Энергия активации, Eэксп, ккал/моль | Энергия активации, Eрасч, ккал/моль | |||
| 10 | 20 | 30 | 40 | |||||
| 1:1 | 0,31 | 22,34 | 0,11 | 0,21 | 0,38 | 0,67 | 10,33 | 10,25 |
| 2:1 | 0,47 | 24,58 | 0,17 | 0,30 | 0,54 | 0,94 | 10,62 | 10,60 |
| 1:2 | 0,18 | 20,52 | 0,09 | 0,17 | 0,31 | 0,54 | 10,38 | 9.98 |
Примечание:  M = M 1 ⋅ μ 1 + M 2 ⋅ μ 2 , ( 14 ) M = M 1 ⋅ μ 1 + M 2 ⋅ μ 2 , ( 14 )  | ||||||||
| где M — молекулярная масса смеси, г/моль; | ||||||||
| M1, M2 — молекулярные массы метанола и воды соответственно, г/моль; | ||||||||
| µ1, µ2 — мольная доля соответственно метанола и воды. | ||||||||
E р а с ч = E 1 ⋅ μ 1 + E 2 ⋅ μ 2 , ( 15 )  | ||||||||
| где Eрасч — расчетная величина энергии активации смеси, ккал/моль; | ||||||||
| E1, E2 — значения энергии активации соответственно метанола и воды (таблица 1), ккал/моль; | ||||||||
| µ1, µ2 — мольная доля соответственно метанола и воды. |
Используя градуировочные зависимости летучести от скорости испарения для температур 10, 20, 30 и 40°С, (фигура 4) и найденные значения скорости испарения смесей для этих температур (таблица 3), можно определить значения летучести для смесей.
Применение искусственных смесей известного состава позволяет рассчитать молекулярную массу смеси и определить давление насыщенного пара смеси с помощью выражения (4). Это позволяет оценить правильность определения летучести смеси, используя результаты расчетов давления смеси на основании закона Рауля. Результаты расчетов приведены в таблице 3.
| Таблица 3 | |||||
| Результаты определения летучести и расчета давления насыщенного пара смеси при температуре 10, 20, 30 и 40°С | |||||
| Объемное соотношение метанола и воды | Определяемая характеристика | Значения определяемой характеристики при температуре, °С | |||
| 10 | 20 | 30 | 40 | ||
| 1:1 | Летучесть, Cmax, мг/л | 22,7 | 42,0 | 83,4 | 125,2 |
| Давление насыщенного пара, P, мм рт.ст. | 18,1 | 34,6 | 71,1 | 110,3 | |
| Расчетное значение давления по закону Рауля, Pрасч, мм рт.ст. | 23,1 | 41,8 | 72,9 | 126,7 | |
| 2:1 | Летучесть, Cmax, мг/л | 31.0 | 54,4 | 104,1 | 173,3 |
| Давление насыщенного пара, P, мм рт.ст. | 22,4 | 40,8 | 80,7 | 138,8 | |
| Расчетное значение давления по закону Рауля, Pрасч, мм рт. ст. | 30,2 | 54,1 | 92,9 | 159,0 | |
| 1:2 | Летучесть, Cmax, мг/л | 19,5 | 36,6 | 74,1 | 99,7 |
| Давление насыщенного пара, P, мм рт.ст. | 15,9 | 31,1 | 68,0 | 95,6 | |
| Расчетное значение давления по закону Рауля, Pрасч, мм рт. ст. | 17,1 | 31,8 | 56,6 | 100,4 |
Анализ данных, приведенных в таблице 3, позволяет сделать вывод о правомерности определения летучести, а по ней и давления насыщенного пара искусственных смесей метанола с водой по найденной градуировочной зависимости летучести от скорости испарения. При этом максимальное отклонение величин давления, рассчитанных по экспериментальным данным, от расчетных значений по закону Рауля во всех случаях не превышает 26%.
Следовательно, предложенный способ определения летучести по скорости испарения на основе термогравиметрического метода может быть использован для оценки летучести смесей жидкостей для любой температуры из диапазона температур исследования.
Это позволило определить теплоту испарения для исследуемых смесей метанола с водой по экспериментально найденным значениям летучести, таблица 4.
Из данных, представленных в таблице 4, следует, что экспериментально найденные значения теплоты испарения для искусственных смесей метанола с водой близки к расчетным значениям, что подтверждает возможность определения теплоты испарения по значениям летучести.
| Таблица 4 | ||
| Значения теплоты испарения для исследуемых смесей метанола с водой по экспериментально найденным значениям летучести | ||
| Объемное соотношение метанола и воды в смеси | Значения теплоты испарения, ккал/моль | |
| ΔHэкспер | ΔHтеор по выражению (16) | |
| 1:1 | 10,84 | 10,25 |
| 2:1 | 10,86 | 10,59 |
| 1:2 | 10,90 | 9,98 |
Примечание: Δ H т е о р = Δ H 1 ⋅ μ 1 + Δ H 2 ⋅ μ 2 , ( 16 )  | ||
| где ΔHтеор. — теплота испарения смеси, ккал/моль; | ||
| ΔH1, ΔН2 — значения теплоты испарения метанола и воды, ккал/моль; | ||
| µ1, µ2 — мольная доля соответственно метанола и воды. |
Таким образом, показано, что, используя гравиметрические данные, полученные на стандартном термогравиметрическом оборудовании, можно оценить летучесть и теплоту испарения исследуемой смеси жидкостей.
1. Способ определения летучести и теплоты испарения смеси жидких веществ по скорости испарения с плоской поверхности, отличающийся тем, что устанавливают корреляционную зависимость значений летучести, рассчитываемых по известным справочным данным, для индивидуальных жидких веществ, выбранных в качестве градуировочных жидкостей, от скорости их испарения, определяемой на основании данных термогравиметрического анализа, осуществляемого в изотермическом режиме при достижении равновесного состояния; для исследуемой смеси определяют скорость испарения и по корреляционной зависимости находят значение летучести; затем, используя зависимость найденных значений летучести от температуры, определяют теплоту испарения смеси жидких веществ в исследуемом интервале температур.
2. Способ по п.1, отличающийся тем, что величину теплоты испарения смеси определяют по величине тангенса угла наклона графика прямолинейной зависимости, абсциссой которого является величина обратной абсолютной температуры, а ординатой — логарифм произведения найденного значения летучести смеси на величину абсолютной температуры.
Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Коэффициент летучести. Стандартные состояния
Коэффициент летучести. Стандартные состояния — раздел Химия, Тонкой химической технологии им. М.В.Ломоносова .





0 
Рис.8.2. Зависимость химического потенциала идеального (1) и реального(2)газов от давления.
Химический потенциал идеального газа линейно зависит от логарифма давления (Рис.8.2). Для реального газа зависимость будет криволинейной. За стандартное состояние идеального газа принимают его состояние при давлении 1 атм (ln p˚= 0). Казалось бы на основании уравнения (8.25), что для реального газа – стандартным будет состояние при летучести, рав-ной единице (ln f ˚= 0,точкаm * ) . На самом деле стандартное состояние одно и то же для обоих газов: f 0 = p 0 = 1. Для того, чтобы придти к стандартному состоянию реальный газ нужно расширить по изотерме до бесконечно малого давления, где реальный и идеальный газы имеют одинаковые свойства, в том числе и химические потенциалы, а затем сжать до р = 1 по изотерме идеального газа. Такое сложное определение стандартного состояния позволяет все отклонения реального газа от идеального выразить через коэффициент летучести g,который связывает летучесть и давление:
f = gp, или g = f/p. (8.26)
Свойства реальных и идеальных газов сближаются по мере уменьше-ния давления lim f/p p®0 = 1. g p®0 = 1. (8.27)
Таким образом, именно коэффициент активность выражает отклонение реального газа от идеального и связан с взаимодействиями, существующими в реальном газе. Отношение летучести к стандартному давлению называется активностью
a = f/f 0 = p/p 0 . (8.28)
8.6.4. Методы определения летучести и коэффициента летучести.
8.6.4.1. Летучесть и коэффициенты летучести можно определять эксперименталь-но, измеряя мольные объемы реального газа в зависимости от давления. Эти объемы отличаются от молных объемов идеального газа на величину α:
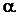
Vреал. = Vид.— 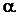
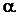
dmT = dG = RT d(lnf) = V dp = (RT/p —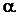
Проинтегрируем уравнение (8.31), приняв за нижний предел бесконечно малое давление, когда f1 ® p1® 0
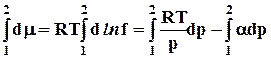
RT ln(f2/p1) = RT ln(p2 /p1) — 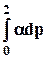
RT lng = — 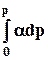
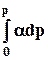
По экспериментальной зависимости величины α от давления графически рассчитывают интеграл в уравнении (8.32) и таким образом находят ln gдля разных давлений
 | |
 |  |
0.8 t
0.5 t


Рис.8.3. Методы определения коэффициентов летучести: а) по уравнению 9.10, б) методом соответственных состояний.
8.6.4.2.Метод соответственных состояний
Как уже указывалось в разделе 8.6.1. разные газы ведут себя одинаково при одинаковых приведенных параметрах p, t. В справочниках имеются номограммы которые позволяют определить коэффициенты летучести разных газов по их приведенным параметрам, т.е. отнесенным критическим.
Таблица 8.1. Летучести и коэффициентов летучести азота при 0 С
| р, атм | ||||||||
| f | 0.9995 | 9.956 | 49.06 | 97.03 | 194.4 | 424.8 | 743.4 | 1.839 |
| g | 0.9995 | 0.9956 | 0.981 | 0.970 | 0.972 | 1.062 | 1.269 | 1.839 |
Лекция № 9
🔍 Видео
Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Самый простой способ понять ХИМИЮ — Типы Кристаллических Решеток и Свойства ВеществаСкачать

Температура и тепловое равновесие. Определение температуры | Физика 10 класс #30 | ИнфоурокСкачать

Типы Химических Связей — Как определять Вид Химической Связи? Химия 9 классСкачать

Предельные вероятности состоянийСкачать

Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать
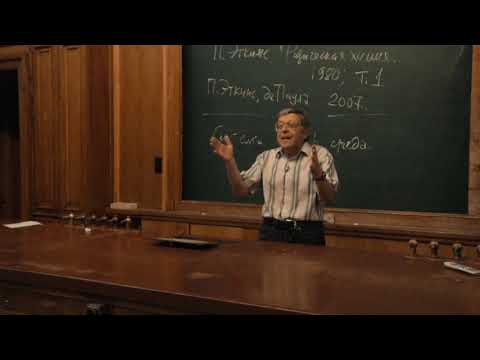
Физическая Химия расчет летучести и коэффициента летучести, активности #physicalchemistryСкачать

Фазовые равновесия | ФизхимияСкачать
"PVT" на русском для начинающих. Часть 6_2Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Химия 9 класс — Как определять Степень Окисления?Скачать

Составление формул соединений. 8 класс.Скачать

Успенская И. А. - Химическая термодинамика и кинетика - Экспериментальные методы определения свойствСкачать

Урок 189. Влажность воздуха. Абсолютная и относительная влажностьСкачать

ВАЛЕНТНОСТЬ 8 КЛАСС ХИМИЯ // Урок Химии 8 класс: Валентность Химических ЭлементовСкачать

ВАЛЕНТНОСТЬ. Графические формулы веществ | Химия | TutorOnlineСкачать

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Успенская И. А. - Химическая термодинамика и кинетика - Химический потенциалСкачать