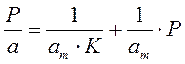Определение констант в уравнении ленгмюра графическим методом (5 видео)

Экспериментальное определение констант

уравнения Ленгмюра

Для того, чтобы воспользоваться уравнением Ленгмюра, необходимо определить величины констант, входящих в это уравнение.

Произведем определенные преобразования уравнения Ленгмюра и представим его в линейной форме, для этого возьмем обратные величины от обеих частей уравнения. Получаем:

, либо, умножив на Р, (2.49)

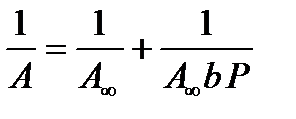
Графическая иллюстрация уравнений Ленгмюра в линейных координатах представлена на рис.2.17:

Рис.2.17. Изотермы Ленгмюра в линейных координатах

На первом графике тангенс угла наклона равен tgα = 1/А_∞b , на втором tgα = 1/А_∞.

Из системы двух уравнений с двумя неизвестными легко определить константы b и А_∞.

Знание емкости монослоя позволяет определить характеристику поверхности адсорбента — удельную поверхность:

где N_a — число Авагадро (24) , S₀ — поверхность, занимаемая одной молекулой адсорбата.

Отклонения от уравнения Ленгмюра

при физической адсорбции могут быть связаны с образованием полислоёв,

при химической — с неоднородностью поверхности.

Условиями применимости уравнения Ленгмюра являются:

1. линейность в координатах 1/А=f(1/P), 1/Г=f(1/С), Р/А=f(P);

3. экспоненциальное уменьшение b с увеличением Т.

Уравнение Ленгмюра может описывать химическую адсорбцию и физическую адсорбцию на границе т/ж, поскольку в этих случаях адсорбция мономолекулярна.

Изотермы адсорбции на поверхности ж/г.

Уравнение адсорбции Гиббса

Вернемся к рассмотрению процессов, идущих на поверхности ж/г, поскольку эта поверхность, безусловно, энергетически однородна.

При растворении в воде ПАВ накапливаются в поверхностном слое, ПИВ — в растворе. Распределение вещества между поверхностным слоем и объемом среды подчиняется принципу минимальной энергии: на поверхности осаждается то вещество, которое обеспечивает наименьшее поверхностное натяжение: в первом случае ПАВ, во втором вода.

Рассмотрим процессы адсорбции этих веществ на границе раздела фаз. Вспомним влияние концентрации растворенных веществ на границе раздела фаз на поверхностное натяжение.

Когда концентрация адсорбата (С_ПАВ) на поверхности больше, чем в объеме среды, то наблюдается уменьшение поверхностного натяжения вследствие образования на границе раздела фаз ориентированного слоя, т.е. адсорбированного слоя. В этом случае Г > 0, при этом величина поверхностной активности > 0. Это отражено на рис.2.18 кривой 1. Г_∞ — величина предельной адсорбции при образовании монослоя.

При недостатке вещества в поверхностном слое Г

Рис 2.18. Изотермы адсорбции ПАВ (1) и ПИВ (2)

Процесс насыщения монослоя тормозится тепловым движением, которое увлекает часть молекул внутрь фазы. С уменьшением Т тепловое движение ослабевает, и избыточная адсорбция Г при той ж концентрации увеличивается (рис.2.19).

Рис. 2.19. Изотермы адсорбции ПАВ при разных температурах

Простых и доступных методов определения избыточной адсорбции Г не существует. Однако на поверхности ж/г легко измерить поверхностное натяжение, а затем использовать очевидную связь между поверхностным натяжением и адсорбцией для расчета избыточной адсорбции Г_ПАВ.

(Вывод уравнения Гиббса. Обычно не даю)

Запишем для единицы площади при постоянной температуре:

, (2.51)

где μ — химический потенциал, равный . (2.52)

μ_о — абсолютный химический потенциал данного компонента, R — универсальная газовая постоянная, Т — температура, a — активность компонента в растворе.

Произведем дифференцирование этого уравнения:

(2.53)

Отсюда: (2.54)

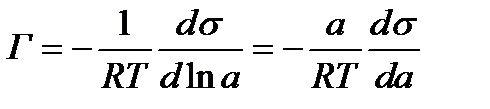
При малых концентрациях а можно заменить на с изаписать

. (2.55)

Уравнение (2.55) Гиббса позволяет рассчитать избыточную адсорбцию Г — разность между концентрацией адсорбтива в поверхностном слое и объемом раствора для концентрации С раствора ПАВ.

Уравнение Гиббса с точки зрения термодинамики универсально и применимо к границам раздела любых фаз.

Уравнение Гиббсабыло многократно подтверждено экспериментально, в частности, методом среза тонких слоев жидкости (с помощью специального ножа — микротома) с последующим анализом их состава, а также — исследованием распределения метки радиоактивного изотопа между поверхностью жидкости и её объёмом.

Измерение адсорбции на твердых адсорбентах обычно производят по убыли концентрации адсорбата в растворе (до и после адсорбции). Поверхность адсорбента, как правило, не велика ΔС составляет лишь несколько процентов от значения самой концентрации. Поэтому для получения достоверных опытных данныx необходимо измерять концентрации с очень большой точностью. В отличие от этого, исследования адсорбции на поверхности жидкость — газ крайне просты. Они сводятся к получению зависимости поверхностного натяжения от концентрации адсорбата, графическому дифференцированию кривой А = f(C) и расчету Г.

Область практического использования уравнения Гиббса для определения величины адсорбции ограничена системами, у которых доступно экспериментальное определение поверхностного натяжения, т.е. системами ж/г и ж/ж.

(Здесь следует показать на графиках, как из зависимости σ = f(C) перейти к Г = f(C)).

Рис. 2.20. Расчет и построение изотермы адсорбции, исходя из изотермы поверхностного натяжения

Правило Дюкло — Траубе:

Это правило работает в растворах гомологических рядов ПАВ и формулируется следующим образом:

С увеличением длины углеводородного радикала на одну группу СН₂, поверхностная активность растет в гомологическом ряду в 3 — 3,5 раза.

Проиллюстрируем это правило графически:

Рис.2.21. Изотермы поверхностного натяжения(а) и адсорбции (б) растворов ПАВ одного гомологического ряда (1,2,3 — число групп -СН₂— в углеводородном радикале)

Обратим внимание на то, что значение Г_∞ для одного гомологического ряда остается постоянным. Это объясняется тем, что емкость монослоя в этом случае зависит только от площади, которую занимает молекула ПАВ в этом слое. В рядах карбоновых кислот, спиртов эта площадь определяется величиной полярной группы, одинаковой для всего ряда ПАВ.

Это правило соблюдается для истинно растворимых ПАВ. Т.к. поверхностная активность определяется для бесконечно разбавленных систем, то легко объяснить ее зависимость от длины углеводородного радикала. Чем длиннее радикал, тем сильнее выталкивается молекула ПАВ из водного раствора, т.к. встраивание радикала в воду увеличивает ΔG, и процесс выхода молекул на поверхность энергетически очень выгоден.

Уравнение Шишковского ( *)

Для случая адсорбции молекул ПАВ на границе раздела фаз можно использовать оба предложенных уравнения адсорбции на однородной поверхности. Приравняем их друг другу:

= (2.56)

Разделим переменные и проинтегрируем эти уравнения:

, (2.57)

, (2.58)

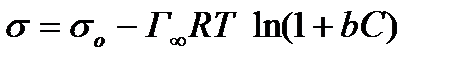
Так как в растворах ПАВ вследствие их высокой поверхностной активности значения абсолютной адсорбции А практически равны избыточной адсорбции Г, поэтому выведенное уравнение может быть записано и в виде: . (2.59)

Полученное уравнение носит название уравнения Шишковского. Первоначально оно было выведено им эмпирически для описания зависимости поверхностного натяжения от концентрации ПАВ:

, (2.60)

В уравнение (2.60) входят коэффициенты В и А, физический смысл которых виден из выше выведенного уравнения (2.59).

Связь между поверхностным натяжением и адсорбцией можно проследить в уравнении Фрумкина (*) :

, (2.61)

из которого следует, что при одинаковой адсорбции все гомологи уменьшают поверхностное натяжение на одну и ту же величину ∆σ.

Различие поверхностной активности в гомологическом ряду ПАВ обусловлено различной особенностью их к адсорбции, т.е. одно и то же значение Г достигается для короткоцепочечных ПАВ при значительно больших С, чем для длинноцепочечных ПАВ. Но если концентрации у гомологов таковы, что их адсорбции одинаковы, то они понижают σна одну и ту же величину.

Видео:Кинетика. О чем говорят графики. БиохимияСкачать

Изучение адсорбции карбоновой кислоты на активированном угле

Министерство по образованию и науке РФ

Федеральное государственное бюджетное образовательное учреждение

Новгородский государственный университет имени Ярослава Мудрого

Институт сельского хозяйства и природных ресурсов

Кафедра химии и экологии

«ИЗУЧЕНИЕ АДСОРБЦИИ КАРБОНОВОЙ КИСЛОТЫ НА АКТИВИРОВАННОМ УГЛЕ»

для специальности 060301.65 − Фармация

1. Получить опытные данные зависимости величины удельной адсорбции (Г) от равновесной концентрации (СРАВН) уксусной кислоты в растворе на активированном угле в качестве адсорбента.

2. Построить изотерму адсорбции в координатах Г–СРАВН.

3. Определить графическим методом константы в уравнении Фрейндлиха и в уравнении Ленгмюра.

2 ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Адсорбцией называется изменение концентрации вещества на границе раздела фаз по сравнению с его концентрацией в объеме фазы.

Причиной адсорбции является ненасыщенность силового поля частиц вблизи границы раздела фаз.

Адсорбция протекает на границах раздела фаз твердое тело – газ, твердое тело – жидкость (раствор), жидкость (раствор) – газ.

Простейший случай адсорбции – адсорбция на границе раздело твердое тело – газ.

Твердое тело, которое адсорбирует, называется адсорбентом. Вещество, которое адсорбируется, называется адсорбтивом или адсорбатом.

В зависимости от природы взаимодействия адсорбента и адсорбтива различают физическую и химическую адсорбцию. Физическая адсорбция обусловлена слабыми силами межмолекулярного взаимодействия. Физическая адсорбция обратима и отличается незначительным тепловым эффектом (до 20 кДж/моль). Химическая адсорбция (хемосорбция) обусловлена силами химического взаимодействия. Химическая адсорбция практически необратима, ее тепловой эффект (до 100 кДж/моль) сопоставим с тепловыми эффектами химических реакций. Независимо от природы адсорбция является экзотермическим процессом.

Количественной характеристикой адсорбции является удельная адсорбция Г, определяемая как количество адсорбтива, адсорбируемое единицей площади поверхности адсорбента (или единицей массы адсорбента).

Величина удельной адсорбции зависит от природы адсорбента и адсорбтива, от температуры и от равновесной концентрации адсорбтива.

Зависимость удельной адсорбции от равновесной концентрации адсорбтива (кислоты) при постоянной температуре называется изотермой адсорбции.

Изотерма может быть описана эмпирическим уравнением Фрейндлиха:

где Г – количество адсорбированного вещества на единицу массы адсорбента (моль/г);

С – равновесная концентрация адсорбтива (моль/л);

К, n – эмпирические константы уравнения

Изотерма мономолекулярной адсорбции описывается уравнением Ленгмюра. Ленгмюровская адсорбция обусловлена силами близкими к химическим, локализована, происходит на активных центрах – особых участках поверхности адсорбента. Активные центры независимы и способны насыщаться: на одном активном центре может адсорбироваться одна молекула. Состоянию насыщения поверхности адсорбента отвечает предельная удельная адсорбция Г∞. Ленгмюровская адсорбция обратима и характеризуется константой адсорбционного равновесия К.

Уравнение изотермы адсорбции Ленгмюра:

Г = , (2)

где Г и Г¥ — удельная адсорбция и предельная удельная адсорбция (моль/ г)

С – равновесная концентрация адсорбтива (моль/ л)

К – константа адсорбционного равновесия.

3 ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ

При выполнении данной лабораторной работы необходимо соблюдать общие правила работы в химической лаборатории.

4 ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

4.1 Приготовление растворов

Путем разбавления исходного 0,4 М раствора уксусной кислоты (муравьиной, пропионовой или другой кислоты по указанию преподавателя) готовят по 100 мл растворов следующих концентраций: 0,3М; 0,2 М; 0,1 М; 0,05 М; 0,025 М.

Для этого рассчитывают объем V1 исходного раствора кислоты с молярной концентрацией C1, необходимый для приготовления объема V2 раствора заданной концентрации С2. При расчете исходят из того, что количество кислоты при разбавлении исходного раствора не изменяется:

Например, для приготовления 100мл 0,3М раствора необходимо взять 75 мл исходного раствора: V1 = 0,3·100/0,4 = 75 мл

Точные концентрации приготовленных растворов устанавливают кислотно-основным титрованием (титрованием раствором щелочи соответствующей концентрации).

Для титрования выбирают раствор щелочи с концентрацией, примерно равной концентрации титруемого раствора.

СН к = (СН NаОН VNаОН)/ VК,

где СН NаОН – эквивалентная (нормальная) концентрация щелочи, моль/л;

СН к– эквивалентная (нормальная) концентрация кислоты, моль/л;

VNаОН– средний объем щелочи, пошедший на титрование пробы кислоты, мл;

VК– объем пробы кислоты, мл.

Для одноосновных кислот эквивалентные и молярные концентрации совпадают СН = СМ.

Видео:Уравнение ЛенгмюраСкачать

Уравнение изотермы адсорбции Ленгмюра

Конечно, предположение, что молекулы адсорбируются с одинаковой вероятностью на любых участках поверхности, в том числе и уже занятых ранее — слишком грубое допущение, пригодное лишь для очень малых степеней покрытия.

Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.

1) Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.

2) Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.

3) Адсорбированные молекулы не взаимодействуют друг с другом.

Простейший вывод уравнения Ленгмюра, данный Кисилевым, основан на рассмотрении химического (в случае хемосорбции) или квазихимического (в случае физической адсорбиии) равновесия молекула газа + свободное место↔адсорбированная молекула.

Для обычного выражения константы равновесия через концентрации участников рассматриваемого процесса необходимо условиться о способах их выражения. Концентрация адсорбированных молекул может быть выражена не только числом адсорбированных молекул на 1 м 2 поверхности, но и в относительных единицах через долю занятой поверхности (степень заполнения поверхности) θ. Тогда, в тех же единицах, концентрация свободных мест 1-θ. Концентрация молекул газа (а молях на миллилитр) может быть заменена пропорциональной ей величиной давления Р (равновесное давление адсорбата в объеме фазы, граничащей с адсорбентом). Такая свобода в выборе единиц рассматриваемых концентраций обусловлена тем, что соответствующие константы пропорциональности могут быть объединены с константой равновесия. Итак, константа равновесия

. (2.6)

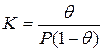
Решение этого уравнения относительно θ приводит к выражению

. (2.7)

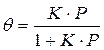
Если а, как и раньше, есть величина адсорбции (моль/см 2 или см 3 /г), а a_m — величина адсорбции, соответствующая полному заполнению поверхности (емкость монослоя, моль/см 2 ), то степень заполнения θ=a/a_m, (2.8)

т.е. 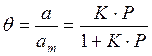, (2.9)

отсюда 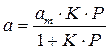(2.10)

В такой форме уравнение Ленгмюра широко известно. Оно содержит две константы: a_m, кратко называемая емкостью монослоя, и K — константа, зависящая от энергии адсорбции и температуры.

Итак, уравнение Ленгмюра – это уравнение монослойной адсорбции на однородной поверхности в отсутствие сил притяжения между молекулами адсорбата.

Посмотрим, какую форму примет уравнение при крайних значениях поверхностной концентрации адсорбированного вещества.

В области малых концентраций, т.е. при малых давлениях, КР >1, и единицей в знаменателе можно пренебречь:

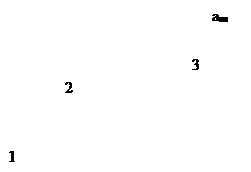
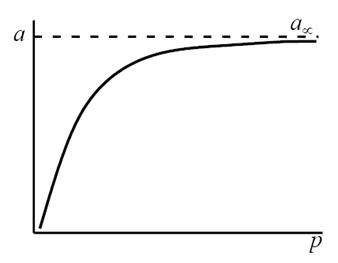
т.е. величина адсорбции стремится к пределу, при котором она уже практически не зависит от давления (участок 3 изотермы адсорбции). В промежуточной области (участок 2) зависимость адсорбции от давления описывается самим уравнением (2.10).

Рис. 2.5. Три участка изотермы адсорбции Ленгмюра

Таким образом, по модели Ленгмюра, вначале адсорбция растет пропорционально давлению газа, затем, по мере заполнения мест на поверхности, этот рост замедляется и, наконец, при достаточно высоких давлениях рост адсорбции практически прекращается, так как покрытие поверхности становится весьма близким к монослойному. Необходимо подчеркнуть, однако, что по этой модели завершение образования монослоя происходит лишь при бесконечно высоком давлении. Форма изотермы адсорбции, предсказываемая уравнением Ленгмюра, экспериментально наблюдается в случае химической адсорбции на однородных поверхностях. Для физической адсорбции такое соответствие наблюдается только в начальной области изотермы. При больших заполнениях не получается предсказываемого теорией приближения к насыщению и изотерма продолжает подъем с ростом давления, причем она становится даже более крутой.

Для удобной проверки приложимости уравнения Ленгмюра к экспериментальным данным преобразуем его в линейную форму. Разделим обе части уравнения (2.10) на Р:

. (2.13)

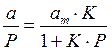
Перевернем дроби по обе части равенства:

. (2.14)

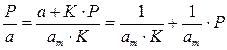
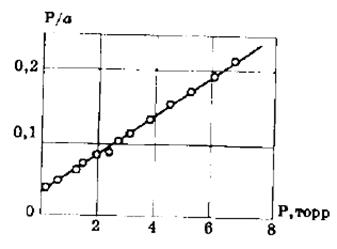
Если по оси абсцисс откладывать Р, а на оси ординат Р/а, то в случае выполнимости уравнения Ленгмюра экспериментальные точки должны укладываться на прямую. Начальной ординатой будет 1/(а_m∙К), тангенсом угла наклона прямой 1/а_m. Из того и другого выражения легко вычислить обе константы a_m и К. Пример такого построения показан на рис. 2.6, где экспериментальные точки для адсорбции бензола на графитированной саже, в соответствии с указанными ранее, легли па прямую только в области малых давлений (до Р/Р₀ =0.1).

Рис. 2.6. Изотерма адсорбции бензола при 20 о С на графитированной саже в координатах линейной формы уравнения Ленгмюра

Имеется немало примеров, когда уравнение Ленгмюра не выполняется. Объясняется это тем, что не оправдываются оба допущения теории об однородности поверхности и отсутствии взаимодействия молекул, особенно первое из них. Тот факт, что имеются случаи адсорбции на реальных неоднородных поверхностях, когда уравнение Ленгмюра все же удовлетворительно описывает экспериментальные данные, Брунауер объясняет тем, что в некотором интервале адсорбция происходит не на всей поверхности адсорбента, а только на части ее, именно на местах с примерно одинаковой теплотой адсорбции. Тогда в этом интервале уравнение Ленгмюра будет справедливо. После того, как эти места заполнены, начинает заполняться следующая серия мест с меньшей теплотой адсорбции. Поэтому для совокупности всех мест поверхности уравнение Ленгмюра может быть непригодно, а для части этих мест — справедливо. Отсюда, выполнимость его для разных адсорбентов зависит от соотношения участков с разной теплотой адсорбции.

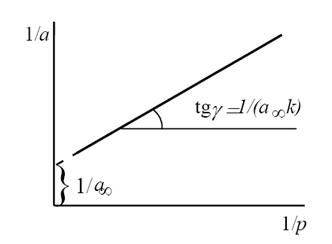
Константы уравнения (2.10) K и a_m могут быть определены графическим способом (рис. 2.7). Для этого уравнение Ленгмюра приводят к следующему линейному виду, разделив единицу на уравнение (2.10):

(2.15)

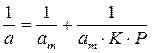
Рис. 2.7. Линейная форма уравнения изотермы Ленгмюра (a_∞=a_m)

Зная емкость монослоя, можно определить удельную поверхность адсорбента S_уд (м 2 /г или см 2 /г) если известна площадь ω, занимаемая частицей в плотном адсорбционном слое (площадь, занимаемая одной молекулой азота в адсорбционном слое ω = 0.162 нм 2 ):

, (16)

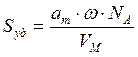
где а_m — емкость монослоя — это количество адсорбата, которое может разместиться в полностью заполненном адсорбционном слое толщиной в 1 молекулу — монослое – на поверхности единицы массы (1г) твердого тела; ω — средняя площадь, занимаемая молекулой адсорбата в заполненном монослое, N_A — число Авогадро (6,022·10 23 молекул/моль); V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию В этом случае используют уравнение БЭТ (Брунауер –Эммет — Теллер).

Пример 2.1. При адсорбции азота на активированном угле при 220К получены следующие данные:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 7 14 23 32 51

Плотность газообразного азота ρ=1,2506 кг/м 3 . Площадь, занимаемая одной молекулой азота в насыщенном монослое, составляет ω = 0.162 нм 2 . V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Постройте изотерму адсорбции в линейных координатах. Графически определите константы а_m и К уравнения Ленгмюра, пользуясь которыми, постройте изотерму Ленгмюра. Определите удельную поверхность активированного угля S_уд.

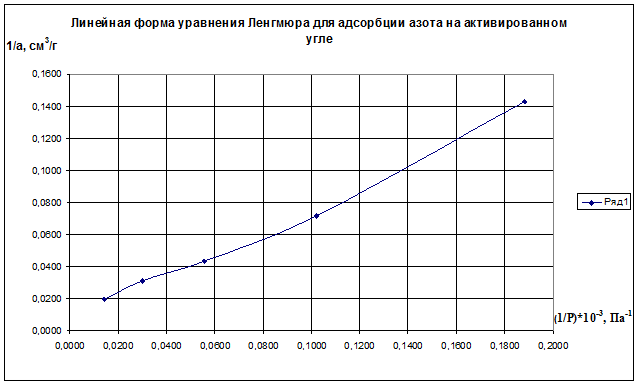
Решение. Линейная форма уравнения Ленгмюра выражается (2.15):

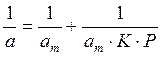
Определим 1/а_m и 1/ р:

(1/р)·10 -3 , Па 0,1883 0,1020 0,0556 0,0303 0,0143

1/а·, см 3 /г 0,143 0,071 0,043 0,031 0,020

Строим график зависимости 1/а=f(1/р)∙10 -3 (рис.2.8). По графику находим 1/а_m как отрезок, отсекаемый прямой на оси ординат, для чего необходимо продлить полученную прямую до пересечения с осью ординат.

Рис.2.8. Линейная форма уравнения Ленгмюра для адсорбции азота на активированном угле

Уравнение прямой y=a+bx, имеет следующее формульное выражение:

Это выражение может быть определено с помощью регрессионного анализа в Microsoft Excel (встроенного пакета Анализ данных — Регрессия по значениям 1/а_m и 1/ р).

Из уравнения получим 1/a_m=0,00698 г/см 3 .

Откуда получим: a_m=143,35 см 3 /г.

Далее находят тангенс угла наклона прямой к оси абсцисс tgα=1/(a_m∙K) по графику (или по уравнению регрессии). tgα=0,70099. Тогда, зная значения a_m и tgα, можно определить K=9,95 кг/м 3 .

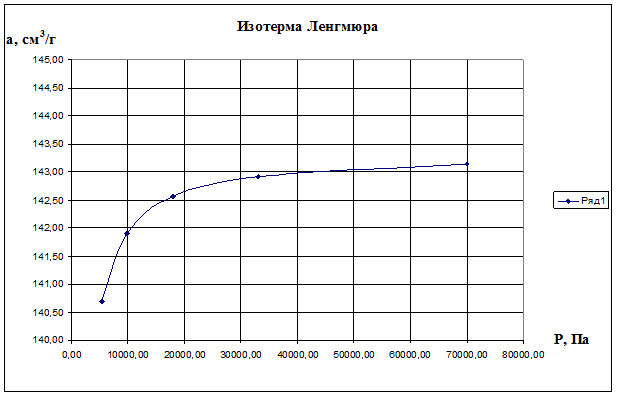
Теперь, зная константы а_m и К уравнения Ленгмюра, построим изотерму Ленгмюра, для чего рассчитаем по формуле (2.10) значения а для различных значений Р и получим:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 140,69 141,90 142,56 142,92 143,15

По данным значениям построим изотерму Ленгмюра а=f(P), представлена на рис.2.9.

Рис. 2.9. Изотерма Ленгмюра а=f(P)

По формуле (2.16) рассчитаем удельную поверхность активированного угля: 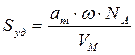и получим S_уд=624,05 м 2 /г.

В случае, когда известна плотность вещества (адсорбента) ρ и молярная масса M, а не известен V_M — молярный объем адсорбата удельную поверхность вещества (активированного угля) находят по формуле:

где a_m выражают в моль/кг.

Для азота М= 0,0280 кг/моль, ρ=1,2506 кг/м 3 .

Из расчетов видно, что два способа расчета S_уд дают почти одинаковые результаты.

Пример 2.2. Удельная поверхность непористой сажи равна 73,7м 2 /кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.

Р, Па 1,03 1,29 1,74 2,50 6,67

а∙10 2 , моль/кг 1,57 1,94 2,55 3,51 7,58

Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.

Решение. Используем линейную форму записи уравнения Ленгмюра, заданную формулой (2.14):