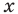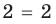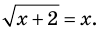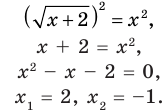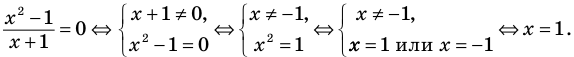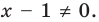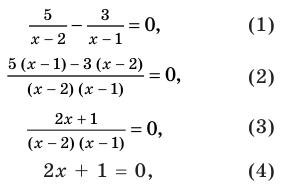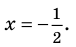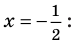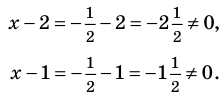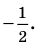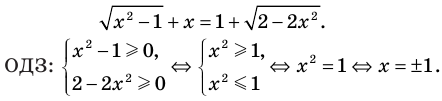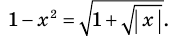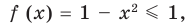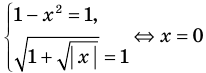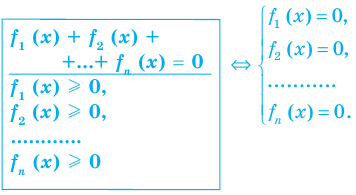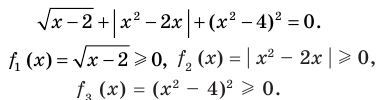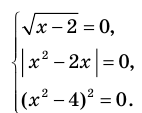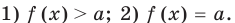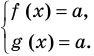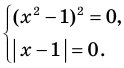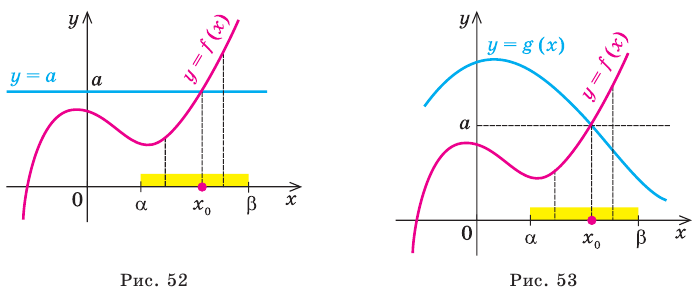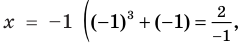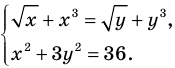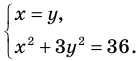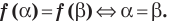- п.1. Количество корней кубического уравнения
- п.2. Количество корней произвольного уравнения
- п.3. Решение неравенств с построением графиков
- Уравнение — определение и вычисление с примерами решения
- Уравнения
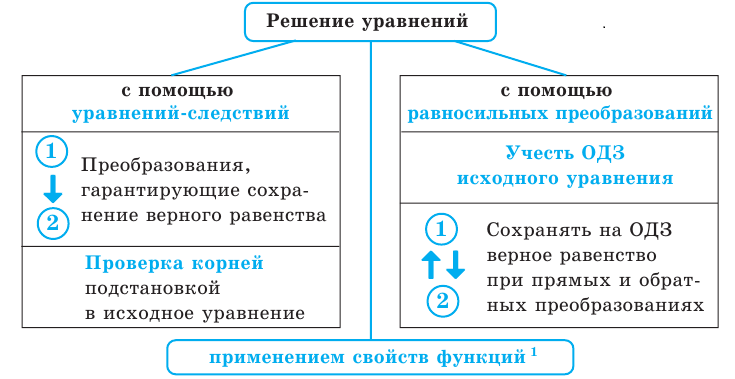
- Уравнения-следствия и равносильные преобразования уравнений
- Понятие уравнения и его корней
- Область допустимых значений (ОДЗ) уравнения
- Методы решения уравнений
- Уравнения-следствия
- Равносильные уравнения
- Причины появления посторонних корней и потери корней при решении уравнений
- Применение свойств функций к решению уравнений
- Конечная ОДЗ
- Оценка левой и правой частей уравнения
- Использование возрастания и убывания функций к решению уравнений
- Найдем число действительных корней. ГДЗ 10 класс Алгебра Алимов Упр 934 параграф 51
- 🔥 Видео
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_=frac<-2bpmsqrt>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
| 1) (x^3+3x^2-4=0) (b^2-3ac=9gt 0 (c=0) ) (f(x)=x^3+3x^2-4 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-4, f(x_2)=0 ) (f(x_1)cdot f(x_2)=0Rightarrow) два корня  | 2) (x^3+3x^2-1=0) (b^2-3ac=9gt 0 ) (f(x)=x^3+3x^2-1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-1, f(x_2)=3 ) (f(x_1)cdot f(x_2)lt 0Rightarrow) три корня  |
| 3) (x^3+3x^2+1=0) (b^2-3ac=9gt 0) (f(x)=x^3+3x^2+1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=1, f(x_2)=5 ) (f(x_1)cdot f(x_2)gt 0Rightarrow) один корень  | 4) (x^3+x^2+x+3=0) (b^2-3ac=1-3lt 0 ) Один корень  |
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения (frac 1x+frac+frac)
б) Найдите число корней уравнения (frac 1x+frac+frac=k)
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac+frac $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac+fracright)=-infty-1-frac13=-infty\ lim_left(frac1x+frac+fracright)=+infty-1-frac13=+infty\ lim_left(frac1x+frac+fracright)=1-infty-frac12=-infty\ lim_left(frac1x+frac+fracright)=1+infty-frac12=+infty\ lim_left(frac1x+frac+fracright)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac+fracright)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac+fracright)=-0-0-0=-0\ lim_left(frac1x+frac+fracright)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac-frac-fraclt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня
Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt=a $$ имеет по крайней мере одно решение.
Исследуем функцию (f(x)=sqrt+sqrt)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt=2sqrt, f(5)=sqrt+0=2)
Первая производная: begin f'(x)=frac<2sqrt>+frac<2sqrt>=frac<2sqrt>-frac<sqrt>\ f'(x)=0 text 2sqrt=sqrtRightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt+sqrt=sqrt+sqrt<frac>=frac<sqrt>=2sqrt end Промежутки монотонности:
| (x) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| (f'(x)) | ∅ | + | 0 | — | ∅ |
| (f(x)) | (2sqrt) | (nearrow ) | max (2sqrt) | (searrow ) | 2 |
Можем строить график:
(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:
| $$ alt 2 $$ | нет решений |
| $$ 2leq alt 2sqrt $$ | 1 решение |
| $$ 2sqrtleq alt 2sqrt $$ | 2 решения |
| $$ a=2sqrt $$ | 1 решение |
| $$ agt 2sqrt $$ | нет решений |
По крайней мере одно решение будет в интервале (2leq aleq 2sqrt).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство (fracgt frac)
Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)
Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac end \ begin 0lt xlt 1\ 2+log_3 xltfrac end end right. \ 2+log_3 xgt fracRightarrow log_3 xgt fracRightarrow log_3 xgt frac\ left[ begin begin xgt 1\ log_3 xgtfrac end \ begin 0lt xlt 1\ log_3 xltfrac end end right. end Исследуем функцию (f(x)=frac=frac=1-frac)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-fracright)=1-frac=+infty\ lim_left(1-fracright)=1-frac=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-fracright)=1-frac=1+0\ lim_left(1-fracright)=1-frac=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-fracright)’=fracgt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac $$ Одна критическая точка 2-го порядка (x=frac12)
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Уравнение — определение и вычисление с примерами решения
Содержание:
Видео:Определить число корней уравнения. Determine the number of roots of the equation.Скачать

Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
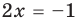
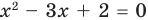
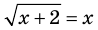
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
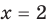
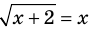
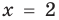
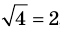
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 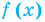
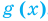
Для уравнения 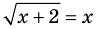
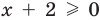
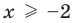
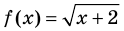

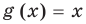
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 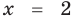
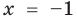
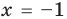
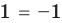
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений



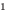
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 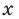
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 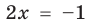
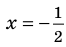
а уравнение 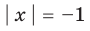
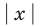
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 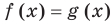
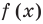
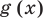
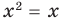
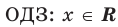
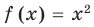
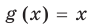
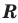
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 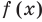
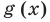
Например, в уравнении 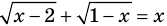
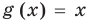
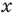
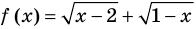
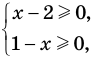
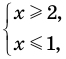
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 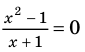
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 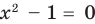
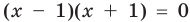
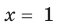
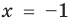
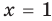
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
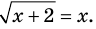
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
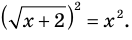
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 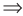
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 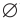
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
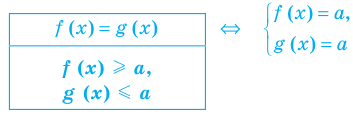
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 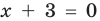
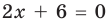
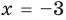
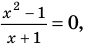
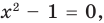
то, как было показано выше, уравнение (3) имеет единственный корень 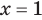
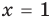
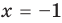
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 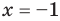
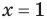
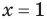
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 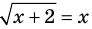
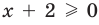

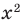
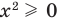
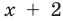


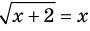
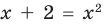
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 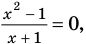
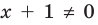
Запись решения в этом случае может быть такой:
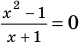
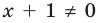
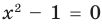
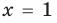
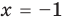
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 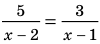
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 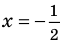
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
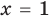
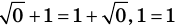
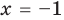
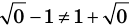
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 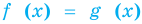


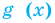
Пример:
►
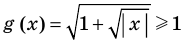
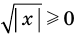
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 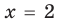
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 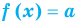
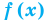
Пример:
Уравнение 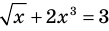
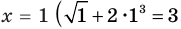
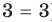
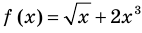
Если в уравнении 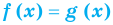
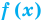
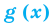
Пример:
Уравнение 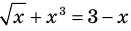
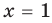
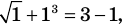
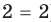
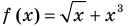

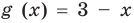
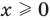
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 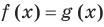
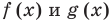
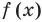
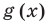
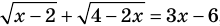
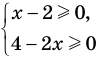
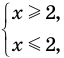


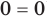


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 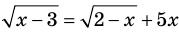
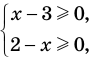
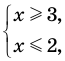
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 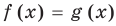
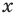
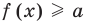
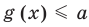
Рассмотрим два случая:
Если 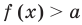
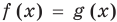
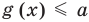
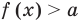
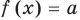
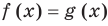
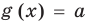
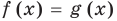
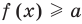
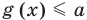
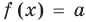
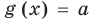
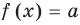
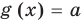
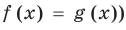
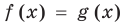
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 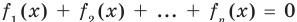
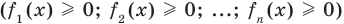
Если предположить, что 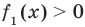

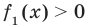
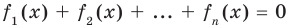
Например, чтобы решить уравнение 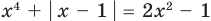
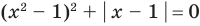
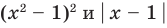
Из второго уравнения получаем 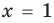
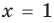
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
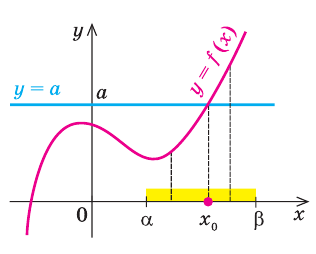
Теорема 1. Если в уравнении 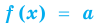
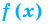
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 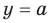
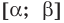
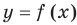
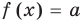
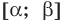
• Если на промежутке 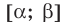
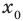
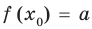
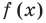
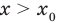
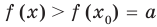
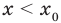
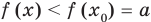
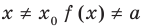
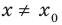
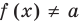
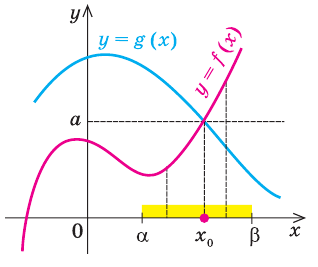
Теорема 2. Если в уравнении 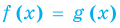
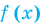
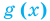
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 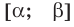
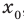
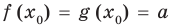
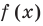
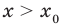
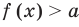
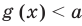
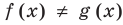
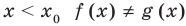
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 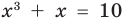
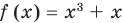

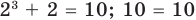
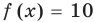
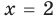
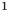

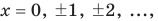
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 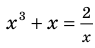
► Сначала следует учесть его ОДЗ: 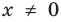
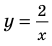
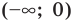
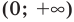
1) При 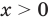
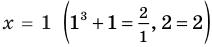
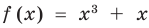

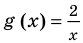

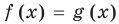
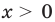
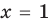
2) При 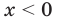
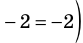
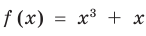
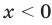
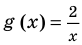
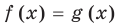
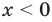
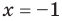
Примеры решения задач:
Пример №424
Решите уравнение 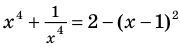
Решение:
► ОДЗ: 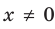
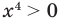
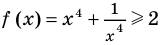
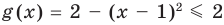
Таким образом, данное уравнение равносильно системе 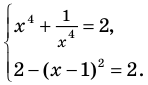


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 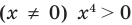
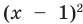
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 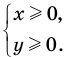
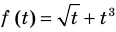
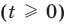
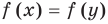
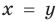
Подставляя 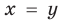
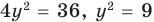
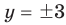

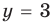
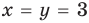
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 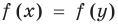
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 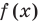
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Определение количества корней уравнения (ДВИ)Скачать

Найдем число действительных корней. ГДЗ 10 класс Алгебра Алимов Упр 934 параграф 51
Доброго дня! А давайте вместе решим?)
Найти число действительных корней уравнения:
1) х4 — 4х8 + 20 = 0;
2) 8х3 — Зх4 — 7 = 0.
Решили уже!
Не понимаю, как решить задачу Гл.V №441.
Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
( Подробнее. )
Доброго дня! Построим график функций?
1) у = x3 — Зх2 + 4;
3) у = -х3 + 4×2 — 4х; ( Подробнее. )
Что это за мнемоническое правило?
Что такое логарифм?
Докажите, что при осевой симметрии плоскости:
а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси ( Подробнее. )
🔥 Видео
Найдите сумму действительных корней уравненияСкачать

Рациональные корни многочлена с целым показателем. 10 класс.Скачать

Число корней уравнения в кольце. Теорема РушеСкачать

Корень n-ой степени из действительного числа и его свойства. 11 класс.Скачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Имеет ли уравнение действительные корни?Скачать

ЧТО ТАКОЕ КОРЕНЬ В N- СТЕПЕНИ? Пригодится для ЕГЭ #shorts #егэ #огэ #математика #корни #mathСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Сколько корней имеет уравнение?Скачать

🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Схема Горнера. 10 класс.Скачать

Курс по численным методам: Отделение действительных корней алгебраический уравнений | Занятие 1Скачать

Как считать корни? #shortsСкачать