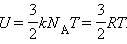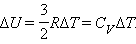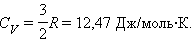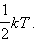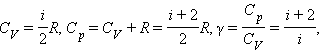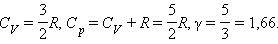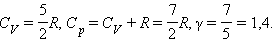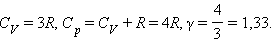Теплоемкостью (С) называют отношение количества теплоты, необходимой для изменения температуры в веществе на бесконечно малую величину:
Такую теплоемкость называют истинной.
При решении практических задач используют среднюю теплоемкость — условную постоянную величину в определенном интервале температур:
В зависимости от единиц количества вещества различают:
- • массовую теплоемкость с, кДж/(кг • К);
- • молярную теплоемкость рс или См, кДжДкмоль-К);
- • объемную теплоемкость С или с’, отнесенную к 1 м 3 газа при нормальных физических условиях (j) = 760 мм рт. ст., t = 0°С), кДж/(м 3 • К) .
Массовая, молярная и объемная теплоемкости связаны между собой следующими зависимостями:
где |i — молекулярная масса вещества, кг/кмоль; vH, рн — удельный объем и плотность вещества при нормальных условиях; 22,4 м 3 /кмоль — объем одного киломоля любого идеального газа при нормальных физических условиях [1] .
Теплоемкость рабочего тела зависит от характера процесса, поэтому тоже является функцией процесса. В различных процессах теплоемкость может принимать значения в пределах -©о 3 смеси газов при нормальных физических условиях находят по формуле
Мольную теплоемкость газовой смеси определяют но аналогичной формуле:
Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Электронная библиотека
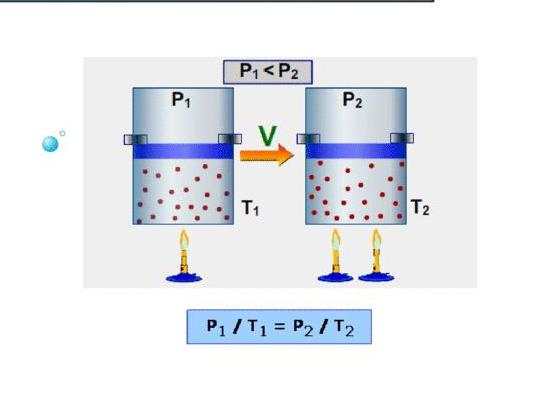
Процесс нагревания или охлаждения может происходить при различных условиях. Рассмотрим процесс нагревания газа одного и того же количества (1 кг) в одинаковых цилиндрах с одинаковыми начальными параметрами (рис. 5.1).
В обоих цилиндрах газ будем нагревать до одинаковой температуры Т2. В первом цилиндре (рис.5.1, а) теплота будет подводиться при постоянном объеме, т.е. процесс будет изохорным. Во втором цилиндре (рис.5.1, б) газ будет расширяться от v1 до v2 при постоянном давлении (р), т.е. процесс будет изобарным.
Рис. 5.1. Изохорный (а) и изобарный (б) процессы
Так как в первом случае газ не расширяется, он не совершает работу и поэтому вся подводимая теплота тратится на повышение внутренней энергии и на повышения давления. Удельное количество теплоты можно определить по формуле:
Во втором цилиндре подведенная к газу теплота расходуется как на повышение температуры, так и на перемещение поршня (т.е. на совершение работы). Удельное количество теплоты в этом случае можно определить по формуле:
Подогрев газа в обоих цилиндрах идет до одинаковой температуры Т2, но во втором случае теплоты необходимо затратить больше на величину работы l, совершенной для перемещения поршня. Тогда:
Известно, что работа (l) при р = const составляет:
Полученная связь между изобарной и изохорной теплоемкостями (5.3) называется уравнением Майера. Зная зависимость между теплоемкостями, можно записать:
Таким образом, в зависимости от того к какой количественной единице вещества относится теплоемкость, различают следующие виды изобарной и изохорной теплоемкостей:
– массовые изобарная и изохорная теплоемкости;
– объемные изобарная и изохорная теплоемкости;
– мольные изобарная и изохорная теплоемкости.
В термодинамических расчетах часто встречается величина ( ), называемая показателем адиабаты и равная отношению изобарной теплоемкости к изохорной:
Значение показателя адиабаты зависит от температуры, но для газов и паров эта зависимость незначительна, и ею пренебрегают, принимая величиной постоянной. Для идеальных газов значение показателя адиабаты принимают равным:
· одноатомных газов – 1,67;
· двухатомных газов – 1,4;
· трех- и многоатомных газов – 1,29.
Точные значения для некоторых газов и водяных паров приводятся в справочниках в зависимости от их температур.
Видео:Адиабатный процесс. 10 класс.Скачать

Изохорная теплоемкость идеального газа
В термодинамике при изучении переходов из начального в конечное состояние некоторой системы важно знать тепловой эффект процесса. С этим эффектом тесно связано понятие теплоемкости. В данной статье рассмотрим вопрос, что понимают под изохорной теплоемкостью газа.
Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Идеальный газ
Идеальным называется такой газ, частицы которого считаются материальными точками, то есть не имеют размеров, но обладают массой, и у которого вся внутренняя энергия состоит исключительно из кинетической энергии движения молекул и атомов.
Любой реальный газ в идеале никогда не будет удовлетворять описанной модели, поскольку его частицы все же имеют некоторые линейные размеры и взаимодействуют между собой с помощью слабых ван-дер-ваальсовых связей или химических связей другого типа. Однако при низких давлениях и высоких температурах расстояния между молекулами велики, а их кинетическая энергия превышает потенциальную в десятки раз. Все это позволяет применять с высокой степенью точности идеальную модель для реальных газов.
Видео:30. Политропические процессыСкачать

Внутренняя энергия газа
Внутренняя энергия любой системы — это физическая характеристика, которая равна сумме потенциальной и кинетической энергии. Поскольку в идеальных газах можно пренебречь потенциальной энергией, то для них можно записать равенство:
Где Ek — энергия кинетическая системы. Используя молекулярно-кинетическую теорию и применяя универсальное уравнение состояния Клапейрона-Менделеева, несложно получить выражение для U. Оно записано ниже:
Здесь T, R и n — абсолютная температура, газовая постоянная и количество вещества соответственно. Величина z — это целое число, показывающее количество степеней свободы, которыми обладает молекула газа.
Видео:Определение отношения теплоемкостей методом Клемана и ДезормаСкачать

Изобарная и изохорная теплоемкость
В физике теплоемкостью называется количество теплоты, которое необходимо предоставить изучаемой системе, чтобы нагреть ее на один кельвин. Справедливо также и обратное определение, то есть теплоемкость — это количество теплоты, которое система выделяет при охлаждении на один кельвин.
Проще всего для системы определить изохорную теплоемкость. Под ней понимают теплоемкость при постоянном объеме. Поскольку система в таких условиях работу не совершает, то вся энергия расходуется на повышение внутренних энергетических запасов. Обозначим изохорную теплоемкость символом CV, тогда можно записать:
То есть изменение внутренней энергии системы прямо пропорционально изменению ее температуры. Если сравнить это выражение, с записанным в предыдущем пункте равенством, то приходим к формуле для CV в идеальном газе:
Данной величиной на практике неудобно пользоваться, поскольку она зависит от количества вещества в системе. Поэтому было введено понятие удельной изохорной теплоемкости, то есть величины, которую рассчитывают либо на 1 моль газа, либо на 1 кг. Обозначим первую величину символом CV n , вторую — символом CV m . Для них можно записать такие формулы:
Здесь M — молярная масса.
Изобарной называется теплоемкость при поддержании постоянного давления в системе. Примером такого процесса является расширение газа в цилиндре под поршнем при его нагревании. В отличие от изохорного, во время изобарного процесса подводимое к системе тепло расходуется на повышение внутренней энергии и на выполнение механической работы, то есть:
Энтальпия изобарного процесса представляет собой произведение изобарной теплоемкости на изменение температуры в системе, то есть:
Если рассмотреть расширение при постоянном давлении 1 моль газа, то первое начало термодинамики запишется в виде:
Последнее слагаемое получено из уравнения Клапейрона-Менделеева. Из этого равенства следует связь между изобарной и изохорной теплоемкостями:
Для идеального газа удельная молярная теплоемкость при постоянном давлении всегда больше соответствующей изохорной характеристики на величину R=8,314 Дж/(моль*К).
Видео:Физика Изучение графиков изопроцессовСкачать

Степени свободы молекул и теплоемкость
Выпишем еще раз формулу для удельной молярной изохорной теплоемкости:
В случае газа одноатомного величина z = 3, поскольку атомы в пространстве могут перемещаться лишь в трех независимых направлениях.
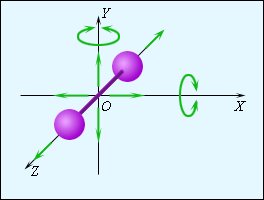
Если же речь идет о газе, состоящем из двухатомных молекул, например, кислород O2 или водород H2, то, помимо поступательного движения, эти молекулы могут еще вращаться вокруг двух взаимно перпендикулярных осей, то есть z будет равно 5.
В случае более сложных молекул для определения CV n следует использовать z=6.
Видео:О.Я. Савченко 5.6.28* | Вывод уравнения политропыСкачать

Определение изобарной и изохорной теплоемкостей вывод уравнения для их соотношения
Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.
Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: – молярная теплоемкость в изохорном процессе () и – молярная теплоемкость в изобарном процессе ().
В процессе при постоянном объеме газ работы не совершает: . Из первого закона термодинамики для газа следует
|
Изменение внутренней энергии газа прямо пропорционально изменению его температуры.
Для процесса при постоянном давлении первый закон термодинамики дает:
|
где – изменение объема 1 моля идеального газа при изменении его температуры на . Отсюда следует:
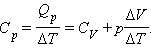 |
Отношение может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
| , |
где – универсальная газовая постоянная. При
| = + . |
Молярная теплоемкость газа в процессе с постоянным давлением всегда больше молярной теплоемкости в процессе с постоянным объемом (рис. 3.10.1).
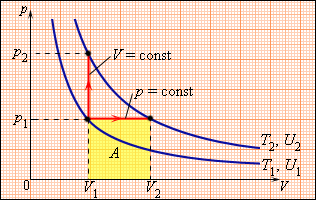 | |||||||||||||||||||||
| Рисунок 3.10.1. Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом играет важную роль в термодинамике. Оно обозначается греческой буквой .
В частности, это отношение входит в формулу для адиабатического процесса (см. §3.9). Между двумя изотермами с температурами и на диаграмме () возможны различные пути перехода. Поскольку для всех таких переходов изменение температуры одинаково, следовательно, одинаково изменение внутренней энергии. Однако, совершенные при этом работы и полученные в результате теплообмена количества теплоты окажутся различными для разных путей перехода. Отсюда следует, что у газа имеется бесчисленное количество теплоемкостей. и – это лишь частные (и очень важные для теории газов) значения теплоемкостей. Термодинамические процессы, в которых теплоемкость газа остается неизменной, называются политропическими . Все изопроцессы являются политропическими. В случае изотермического процесса , поэтому . В адиабатическом процессе , следовательно, . Следует отметить, что «теплоемкость», как и «количество теплоты» – крайне неудачные термины. Они достались современной науке в наследство от теории теплорода , господствовавшей в XVIII веке. Эта теория рассматривала теплоту как особое невесомое вещество, содержащееся в телах. Считалось, что оно не может быть ни создано, ни уничтожено. Нагревание тел объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Теория теплорода несостоятельна. Она не может объяснить, почему одно и то же изменение внутренней энергии тела можно получить, передавая ему разное количество теплоты в зависимости от работы, которую совершает тело. Поэтому лишено физического смысла утверждение, что «в данном теле содержится такой-то запас теплоты». В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией
Внутренняя энергия 1 моля идеального газа равна произведению
При изменении температуры на внутренняя энергия изменяется на величину
Коэффициент пропорциональности между и равен теплоемкости при постоянном давлении:
Это соотношение хорошо подтверждается в экспериментах с газами, состоящими из одноатомных молекул (гелий, неон, аргон). Однако, для двухатомных (водород, азот) и многоатомных (углекислый газ) газов это соотношение не согласуется с экспериментальными данными. Причина такого расхождения состоит в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию не только поступательного, но и вращательного движения молекул.
|







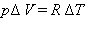 или
или 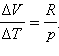
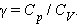
 поступательного движения молекул и абсолютной температурой :
поступательного движения молекул и абсолютной температурой :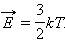
 на число Авогадро :
на число Авогадро :