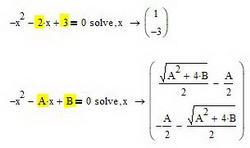Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно пятидесяти. В первой части этого раздела описаны процедуры решения систем уравнений. В заключительной части приведены примеры и проведено обсуждение некоторых часто встречающихся ошибок. Результатом решения системы будет численное значение искомого корня. Для символьного решения уравнений необходимо использовать блоки символьного решения уравнений. При символьном решении уравнений искомый корень выражается через другие переменные и константы.
Для решения системы уравнений выполните следующее:
- Задайте начальные приближения для всех неизвестных, входящих в систему уравнений. Mathcad решает уравнения при помощи итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению.
- Напечатайте ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. При печати слова Given можно использовать любой шрифт, прописные и строчные буквы. Убедитесь, что при этом Вы не находитесь в текстовой области или параграфе.
- Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений стоит символ =. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов ,
, и
.
- Введите любое выражение, которое включает функцию Find. При печати слова Find можно использовать шрифт любого размера, произвольный стиль, прописные и строчные буквы.
| Find(z1, z2, z3, . . . ) | Возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных. |
Функция Find возвращает найденное решение следующим образом:
- Если функция Find имеет только один аргумент, то она возвращает решение уравнения, расположенного между ключевым словом Given и функцией Find.
- Если функция Find имеет более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1, z2) возвращает вектор, содержащий значения z1 и z2 , являющиеся решением системы уравнений.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называются блоком решения уравнений.
На Рисунке 5 показан рабочий документ, который использует блок решения уравнений для решения одного уравнения с одним неизвестным. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент. Для решения одного уравнения с одним неизвестным можно также использовать функцию root, как показано ниже:
Рисунок 5: Блок решения уравнений для одного уравнения с одним неизвестным.
Между ключевым словом Given и функцией Find в блоке решения уравнений могут появляться выражения строго определенного типа. Ниже приведен список всех выражений, которые могут быть использованы в блоке решения уравнений. Использование других выражений не допускается. Эти выражения часто называются ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные выражения, а через z и w обозначены любые скалярные выражения.
| Условие | Как ввести | Описание |
| w = z | [Ctrl] = | Булево равенство возвращает 1, если операнды равны; иначе 0 |
| x > y | > | Больше чем. |
| x |
Следующие выражения недопустимы внутри блока решения уравнений:
- Ограничения со знаком
.
- Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
- Неравенства вида a -15 .
Причиной появления этого сообщения об ошибке может быть следующее:
- Поставленная задача может не иметь решения.
- Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число. Если решение задачи комплексное, то оно не будет найдено, если только в качестве начального приближения не взято также комплексное число. На Рисунке 11 приведен соответствующий пример.
- В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Метод поиска решения, который используется в Mathcad, не позволяет в этом случае построить следующее приближение, которое бы уменьшало невязку. Для поиска искомого решения пробуйте использовать различные начальные приближения или добавьте ограничения на переменные в виде неравенств, чтобы обойти точку локального минимума.
- В процессе поиска решения получена точка, которая не является точкой локального минимума, но из которой метод минимизации не может определить дальнейшее направление движения. Метод преодоления этой проблемы — такой же, как для точки локального минимума: измените начальное приближение или добавьте ограничения в виде неравенств, чтобы миновать нежелательную точку остановки.
- Возможно, поставленная задача не может быть решена с заданной точностью. Если значение встроенной переменной TOL слишком мало, то Mathcad может достигнуть точки, находящейся достаточно близко к решению задачи, но уравнения и ограничения при этом не будут выполнены с точностью, задаваемой переменной TOL. Попробуйте увеличить значение TOL где-нибудь выше блока решения уравнений.
Что делать, когда имеется слишком мало ограничений
Если количество ограничений меньше, чем количество переменных, Mathcad вообще не может выполнить блок решения уравнений. Mathcad помечает в этом случае функцию Find сообщением об ошибке “слишком мало ограничений”.
Задача, аналогичная той, которая приведена на Рисунке 12, называется недоопределенной. Ограничений в ней меньше, чем переменных. Поэтому ограничения не содержат достаточной информации для поиска решения. Поскольку функция Find имеет пять аргументов, Mathcad определяет, что требуется решить два уравнения с пятью неизвестными. Вообще говоря, такая задача обычно имеет бесконечное число решений.
При использовании блока решения уравнений в Mathcad необходимо задать количество уравнений по крайней мере не меньшее, чем число искомых неизвестных. Если зафиксировать значения некоторых переменных, удастся решить уравнения относительно оставшихся переменных. На Рисунке 13 показано, как, зафиксировав часть переменных, решить недоопределенную задачу из Рисунка 12. Поскольку функция Find содержит только два аргумента, z и w, Mathcad определяет переменные x, y и v как имеющие фиксированные значения 10, 50 и 0 соответственно. Блок решения уравнений становится в этом случае корректно определенным, потому что теперь имеются только две неизвестных, z и w, и два уравнения.
Рисунок 12: Функция Find имеет пять аргументов, поэтому Mathcad определяет, что требуется решить два уравнения с пятью неизвестными.
Рисунок 13: Проблема может быть решена, если уменьшить количество аргументов функции Find.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
- Решение уравнений в MathCad
- Использование метода Given — Find:
- Использование метода Solve:
- Опишите структуру блока решения уравнений mathcad
- Справочный материал и примеры
- Функция root, блоки Given…Find, Given…Minerr
- Решение полиномиальных уравнений. Функция polyroots
- Порядок выполнения лабораторной работы
- Контрольные вопросы
- Лабораторная работа №5. Mathcad. Решение систем уравнений
- Справочный материал и примеры
- Блоки Given … Find , Given … Minerr
- Решение систем линейных уравнений
- Порядок выполнения лабораторной работы
- 🎦 Видео
Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Решение уравнений в MathCad
Для решения уравнений в Mathcad можно воспользоваться двумя способами:
Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Использование метода Given — Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
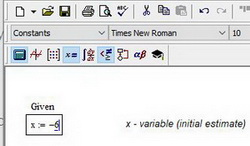
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
После уравнения вводится функция Find(x) (где х — переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах
Для получения результата, после Find(x) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 3). Причем, если вы используете символ «→«, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ «=«, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель «Evaluation»
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата
Рис. 5. Результат символьного решения уравнения
Видео:Mathcad-09. Пример: уравненияСкачать

Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа «ровно» из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given — Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Видео:Mathcad Prime (часть 2)Скачать

Опишите структуру блока решения уравнений mathcad
Цель работы: Получить навыки решения алгебраических уравнений средствами системы Mathcad .
Видео:8. MathCad. Решение систем линейных алгебраических уравненийСкачать

Справочный материал и примеры
Система Mathcad обладает широкими возможностями численного решения уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
· отделение корней − определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
· уточнение корней − нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL ( Convergence Tolerance − Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL , тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build — In Variables ( Встроенные переменные) или присваиванием, например, 
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root , которая в общем виде задается
и возвращает значение переменной x , при котором функция f ( x ) обращается в ноль. Аргументы функции root :
· f ( x ) – функция левой части уравнения f ( x ) = 0;
· x – переменная, относительно которой требуется решить уравнение;
· a , b (необязательные) – действительные числа, такие что a b , причем на интервале [ a, b] находится только один корень.
Если функция root не может найти корни уравнения, то рекомендуется уточнить начальное приближение по графику, изменить границы интервала [ a , b ] нахождения корня или увеличить значение системной переменной TOL .
Для решения уравнений используются функции Find или Minerr . Они входят в состав вычислительного блока, который включает в себя ключевое слово Given , набор уравнений и неравенств и завершается одной из указанных вычисляющих функций в составе какого-нибудь выражения.
возвращает значения неизвестных x 1 , x 2 , … , обращающих уравнения в верные тождества, т. е. возвращает точное решение системы уравнений или одного уравнения в частном случае.
Если в результате поиска не может быть получено решение с заданной точностью, то функция F ind выдает сообщение об ошибке. В этом случае можно использовать функцию
возвращающую приближенное решение одного уравнения. При использовании m iner r необходимо производить дополнительную проверку достоверности результатов решения.
Порядок применения блоков Given … Find , Given … Minerr для численного решения уравнений:
1 Всем неизвестным, входящим в систему, задается начальное приближение.
2 При необходимости присваиваются требуемые значения системным переменным TOL и CTOL ( Constraint Tolerance − Допуск ограничения).
3 Печатается ключевое слово Given , которое указывает Mathcad, что далее следует система уравнений.
4 Задаются уравнения и ограничения на поиск решения в виде неравенств (если они имеются) в любом порядке, каждое в отдельном формульном блоке, причем для записи используются операторы отношения палитры Boolean ( Логические). Допускается использование двусторонних неравенств вида a ≤ x ≤ b .
5 Применяется функция Find или Minerr в составе какого-нибудь выражения. В качестве аргументов через запятую перечисляются имена входящих в систему переменных в том порядке, в котором должны быть расположены в ответе соответствующие им корни.
6 В случае использования функции Minerr выполняется проверка.
Внутри блока решения недопустимы следующие операции и выражения:
· выражения, содержащие знак ≠;
· локальное (:=) или глобальное (≡) определение переменных и функций, за исключением выражения, в состав которого входит функция Find или Minerr ;
· другой блок решения. Каждый блок должен содержать только одно слово Given и одну решающую функцию.
В случае появления ошибки, означающей, что решение не было найдено, рекомендуется изменить начальное приближение или значения системных переменных TOL и CTOL .
Пример к заданию 1
Пример 1. Решить уравнение 
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f ( x ) , равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
Снизу по оси абсцисс наберем x , а сбоку по оси ординат введем f ( x ).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f ( x ). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format ( Формат). Установим пересечение осей графика ( Crossed − Т олько оси), добавим вспомогательные линии по координатным осям ( Grid Lines − Вспомогательные линии). Отменим при этом автосетку ( Autogrid − Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply ( Применить) и ОК.
После указанных преобразований график функции f ( x ) будет выглядеть следующим образом:
Из графика функции f ( x ) видно, что уравнение 
Этап отделения корней завершен.
Уточним теперь корни уравнения различными способами.
1-й способ. Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root :
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
2-й способ. Присвоим начальное приближение переменой x для уточнения третьего корня:
Напечатаем служебное слово Given . Ниже наберем f ( x ) = 0, используя логический знак равенства с панели Boolean ( Логические) − комбинация клавиш Ctrl + =. Еще ниже напечатаем выражение x 3 = Find ( x ) и вывод значения третьего корня x 3 =.
Уточнение корня уравнения с помощью блока Given … Find выглядит следующим образом:
3-й способ. Уточнение корня уравнения с помощью блока Given … Minerr осуществляется аналогично предыдущему случаю:
Примечание − Д ля уточнения корня в данном примере установлена точность 0,0001. Поэтому целесообразно изменить формат вывода результатов (4 знака после десятичного разделителя) в окне форматирования результатов на вкладке Number Format .
Решение полиномиальных уравнений. Функция polyroots
Для решения полиномиальных уравнений вида
или нахождения всех корней полинома степени n, используют функцию
возвращающую вектор-столбец длины n, состоящий из корней полинома, как действительных, так и комплексных. Аргументом функции polyroots является вектор v длины n + 1
1) задать полином;
2) выделить переменную синим управляющим курсором;
3) создать вектор коэффициентов полинома, выполнив последовательность команд главного меню Symbolics / Polynomial Coefficients ( Символика / Коэффициенты полинома);
4) вырезать вектор коэффициентов полинома в буфер обмена;
5) задать переменную v и присвоить ей значение вектора коэффициентов полинома, вставив его непосредственно из буфера обмена;
6) применить функцию polyroots ( v ) в каком-нибудь выражении, например , 
7) получить вектор корней полинома: X =.
Доступ к каждому отдельному корню − элементу вектора X − осуществляется с помощью индекса, например, Xi =.
Пример к заданию 2
Пример 2. Решить уравнение 
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients ( Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку В ырезать 
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку В ставить 
Для получения результата напечатаем polyroots ( v ) =:
Видео:MathCAD Решение системы уравненийСкачать

Порядок выполнения лабораторной работы
1 Загрузить Mathcad.
2 Сохранить в личной папке на диске z : в папке Mathcad LAB 4 новый документ с именем ФИО_4, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы ( Ctrl + S ).
3 Вставить текстовую область и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений в Math cad .
4 В новой текстовой области ввести фамилию, имя, отчество и номер варианта.
5 Задание 1. Решить уравнение (таблица 1) с точностью 10 -5 : отделить корень графически и уточнить с помощью функции root ; блока Given … Find ; блока Given … Minerr .
Таблица 1 − Нелинейные уравнения
6 Задание 2. Решить полиномиальное уравнение (таблица 2).
Таблица 2 − Полиномиальное уравнение
Видео:MathCAD. Given - FindСкачать

Контрольные вопросы
1 Как найти начальное приближение корней уравнений?
2 Какие функции для решения одного уравнения известны в Mathcad? В чем их отличие?
3 Как системная переменная TOL влияет на решение уравнения?
4 Что такое вычислительный блок и какова его структура?
5 Какой знак равенства используется в блоке решения? Какой комбинацией клавиш вставляется в документ?
6 Какие выражения недопустимы внутри блока решения уравнения?
Видео:Решение СЛАУ в пакете MathCadСкачать

Лабораторная работа №5. Mathcad.
Решение систем уравнений
Цель работы: Получить навыки решения систем линейных и нелинейных уравнений средствами системы Mathcad .
Видео:MathCAD Решение уравнений с помощью функции root 2 вариантСкачать

Справочный материал и примеры
Система Mathcad обладает широкими возможностями численного решения систем уравнений.
Блоки Given … Find , Given … Minerr
Для решения систем нескольких уравнений и неравенств используются функции Find или Minerr . Они входят в состав вычислительного блока, который включает в себя ключевое слово Given , набор уравнений и неравенств и завершается одной из указанных вычисляющих функций в составе какого-нибудь выражения.
возвращает значения неизвестных x 1 , x 2 , … , обращающих уравнения в верные тождества, т. е. возвращает точное решение системы уравнений. Для системы из n уравнений с n неизвестными решение возвращается в виде вектора, состоящего из n элементов.
Если в результате поиска не может быть получено решение с заданной точностью, то функция F ind выдает сообщение об ошибке. В этом случае можно использовать функцию
возвращающую приближенное решение системы уравнений (число уравнений должно быть равно числу неизвестных). При использовании m iner r необходимо производить дополнительную проверку достоверности результатов решения системы.
Порядок применения блоков Given … Find , Given … Minerr для численного решения систем уравнений:
7 Всем неизвестным, входящим в систему, задается начальное приближение.
8 При необходимости присваиваются требуемые значения системным переменным TOL и CTOL ( Constraint Tolerance − Допуск ограничения).
9 Печатается ключевое слово Given , которое указывает Mathcad, что далее следует система уравнений.
10 Задаются уравнения и ограничения на поиск решения в виде неравенств (если они имеются) в любом порядке, каждое в отдельном формульном блоке, причем для записи используются операторы отношения палитры Boolean ( Логические). Допускается использование двусторонних неравенств вида a ≤ x ≤ b .
11 Применяется функция Find или Minerr в составе какого-нибудь выражения. В качестве аргументов через запятую перечисляются имена входящих в систему переменных в том порядке, в котором должны быть расположены в ответе соответствующие им корни.
12 В случае использования функции Minerr выполняется проверка.
Внутри блока решения недопустимы следующие операции и выражения:
· выражения, содержащие знак ≠;
· локальное (:=) или глобальное (≡) определение переменных и функций, за исключением выражения, в состав которого входит функция Find или Minerr ;
· другой блок решения. Каждый блок должен содержать только одно слово Given и одну решающую функцию.
В случае появления ошибки, означающей, что решение не было найдено, рекомендуется изменить начальное приближение или значения системных переменных TOL и CTOL .
Пример к заданию 1
Пример 1. Решить систему уравнений
Отделим решения системы графически. Определим две функции аргументов х и y соответственно, выразив для этого из первого уравнения системы у , а из второго − х. Для более детального построения графика создадим ряды значений каждой из этих ранжированных переменных:
Вставим графическую область. Аргументы по оси абсцисс и ординат введем через запятую. После форматирования график выглядит так:
Точка пересечения линий графиков функций является решением системы. Укажем приблизительное значение абсциссы и ординаты точки пересечения в качестве начального приближения:
Напечатаем ключевое слово Given , затем уравнения системы, каждое в отдельном блоке с использованием логического знака равенства ( CTRL + =). Решение уточним с помощью функции Minerr :
Так как Minerr находит приближенное решение системы, то необходимо сделать проверку. Для этого зададим значение системной переменной ORIGIN :=1. Первый элемент вектора X − это значение переменной x , а второй − значение переменной y . Подставим их в левую часть системы и вычислим, чему равна правая, используя обычный знак «=» вывода результата:
Полученные значения совпадают с заданными. Значит, система решена правильно.
Решение систем линейных уравнений
Рассмотрим систему линейных алгебраических уравнений:
В матричном виде ее можно записать Ax = b , где
– матрица коэффициентов при неизвестных системы (матрица левой части системы);
− столбец свободных членов.
Как известно, система линейных алгебраических уравнений имеет решение, если ее определитель отличен от 0: 
Умножим обе части матричного уравнения Ax = b на обратную матрицу коэффициентов при неизвестных системы A -1 слева: 


Этот прием используется в Mathcad так:
1) задается матрица коэффициентов при неизвестных системы A ;
2) задается столбец свободных членов b ;
3) вводится формула для нахождения решения системы 
4) выводится вектор решений системы 
Кроме того, пакет Mathcad имеет встроенную функцию
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному , но вместо формулы 

Реализовать метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref ( M ), возвращающая ступенчатый вид матрицы M . Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given … Find , Given … Minerr . При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Пример к заданию 2
Пример 2. Решить систему линейных уравнений 
1-й способ. Использование блока Given … Find .
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given . Установим визир (курсор) ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства ( Ctrl + =).
После ввода уравнений системы напечатаем X : = Find ( x , y , z ) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given … Minerr .
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой.
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А , состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A : = , вызовем окно создания массивов ( Ctrl + M ). Число строк ( Rows ) и столбцов ( Columns ) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b : =, затем вставим шаблон матрицы( Ctrl + M ), где количество строк ( Rows) равно 3, а количество столбцов ( Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve :
Решение системы с помощью функции rref можно представить так:
В последнем случае матрица AR , полученная путем объединения матрицы при неизвестных системы и столбца свободных членов, является расширенной матрицей системы.
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение 
Видео:Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Порядок выполнения лабораторной работы
7 Загрузить Mathcad.
8 Сохранить в личной папке на диске z : в папке Mathcad LAB 5 новый документ с именем ФИО_5, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы ( Ctrl + S ).
9 Вставить текстовую область и ввести в поле документа текст:
Лабораторная работа № 5
Решение систем уравнений в Math cad .
10 В новой текстовой области ввести фамилию, имя, отчество и номер варианта.
11 Задание 1. Решить систему уравнений (таблица 1), отделив решение графически и уточняя с помощью блока Given … Minerr . Сделать проверку.
Таблица 1 − Нелинейные системы уравнений
🎦 Видео
Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

MathCAD Решение системы линейных уравнений матричным методомСкачать
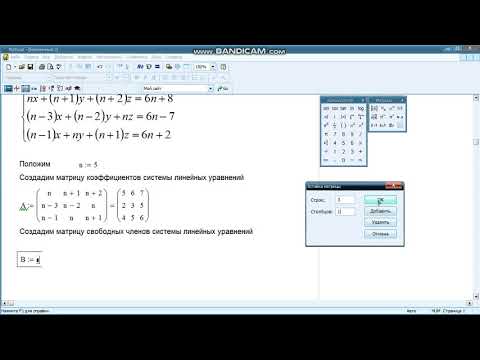
Ключевое слово solve в MathCAD 14 (26/34)Скачать

Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать
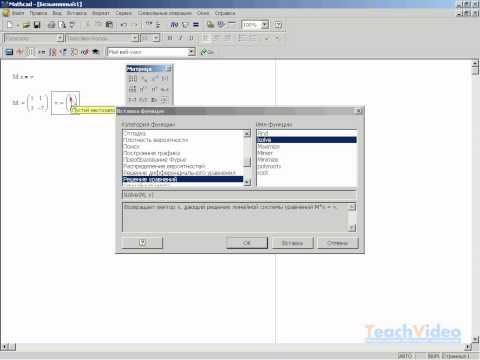
Приближенное решение систем уравнений в MathCAD 14 (30/34)Скачать

4 Метод простой итерации Mathcad Решение системы линейных уравнений СЛАУСкачать

Решение СЛУ MathCad Prime 4 0Скачать

Пример решения уравнения в MathCAD 14 (33/34)Скачать

 , и
, и 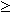 .
.
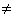 .
.