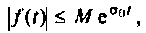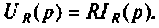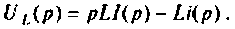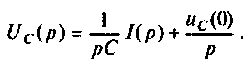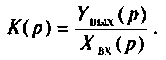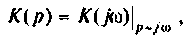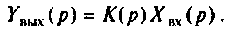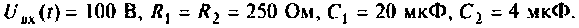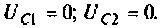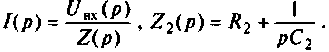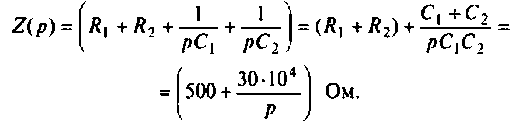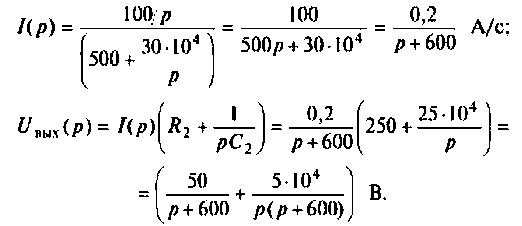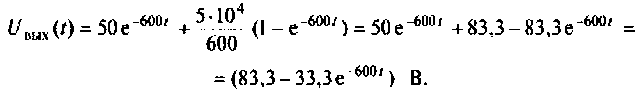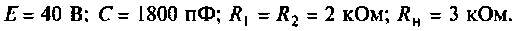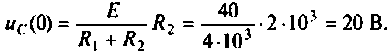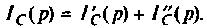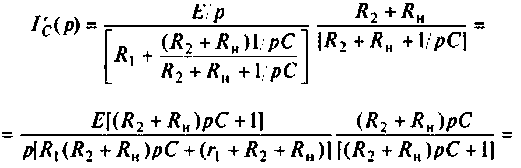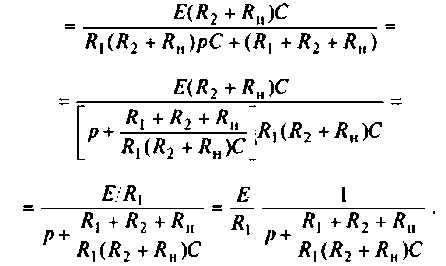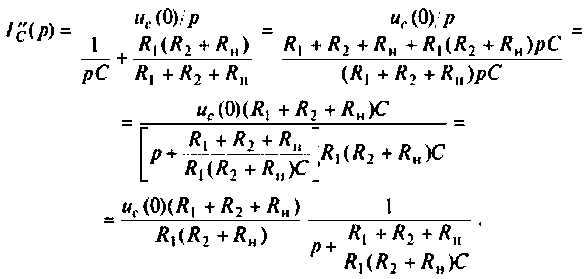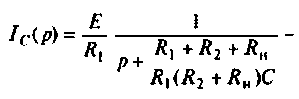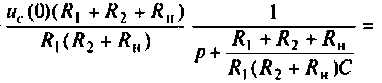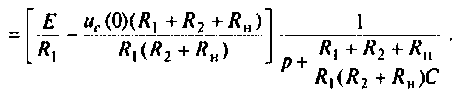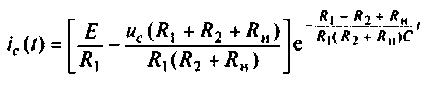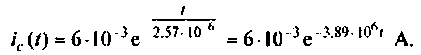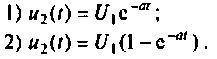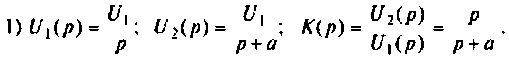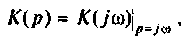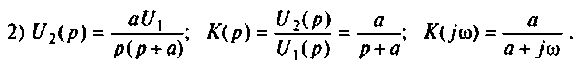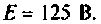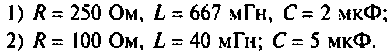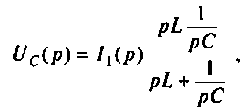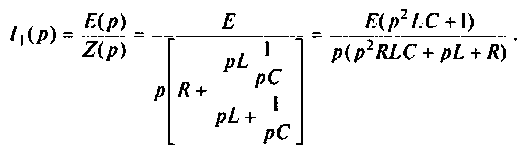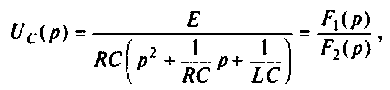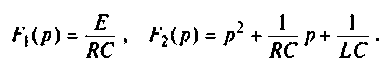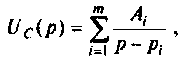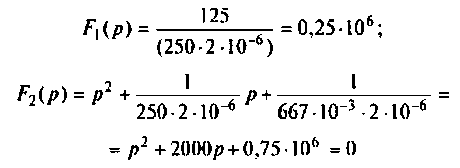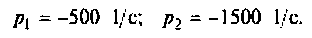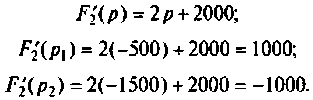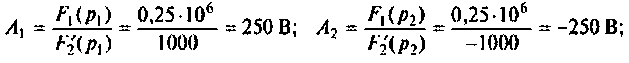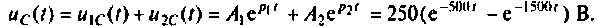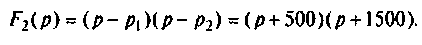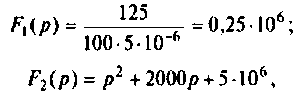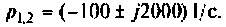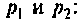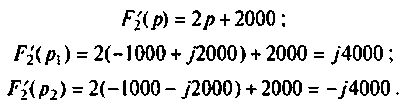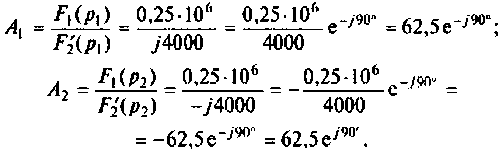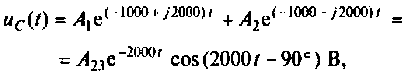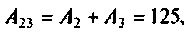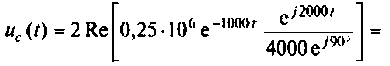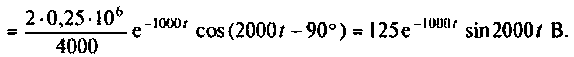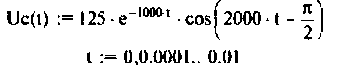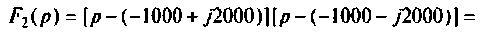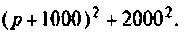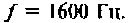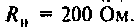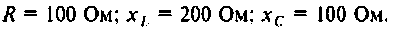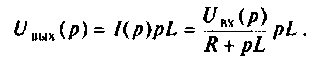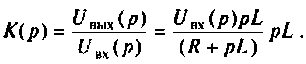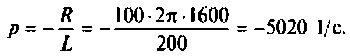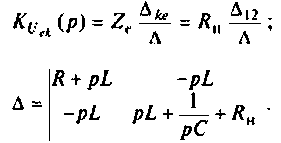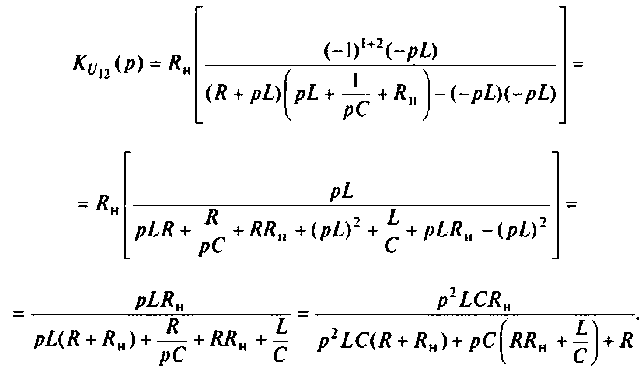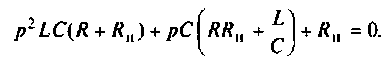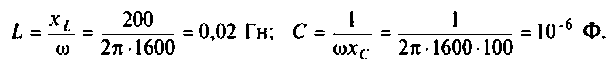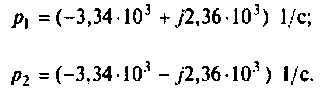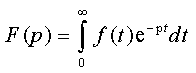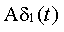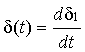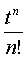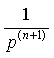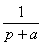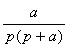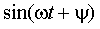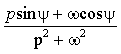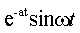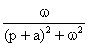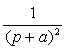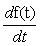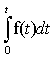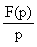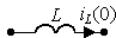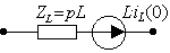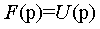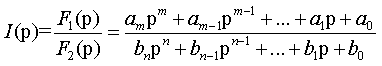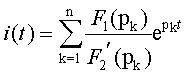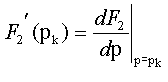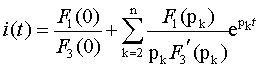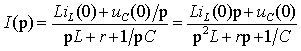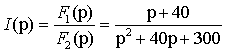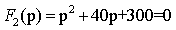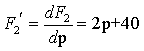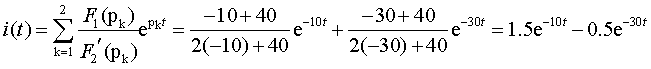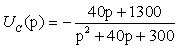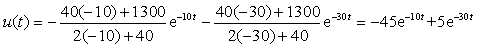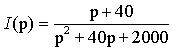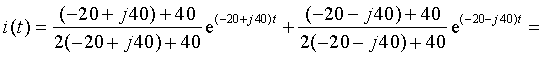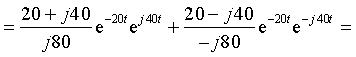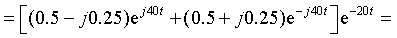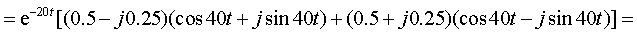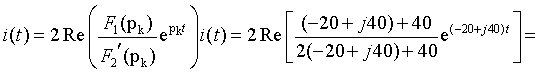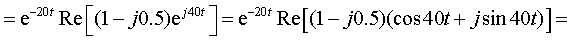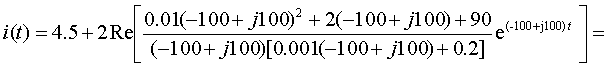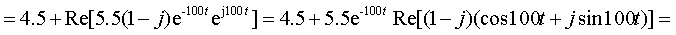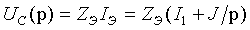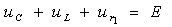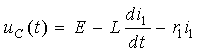Содержание:
Операторный метод расчета переходных процессов:
Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.
Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного
Переход от функции вещественного переменного t к функции комплексного переменного p осуществляется с помощью прямого преобразования Лапласа
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа
Функцию 
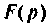
Напомним, что для того чтобы функция 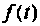
- удовлетворяла условиям Дирихле;
- была равна нулю для отрицательных значений t, т. е. при
- в интервале
не возрастала быстрее, чем некоторая показательная функция
где 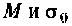
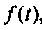
Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.
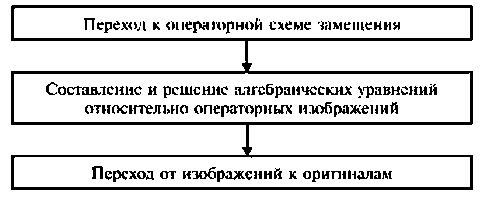
Особенностью метода является необходимость выполнения трех этапов:
Видео:Схемы замещения четырехполюсниковСкачать

Эквивалентные операторные схемы замещения элементов
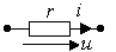
Активное сопротивление:
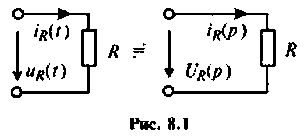
На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде
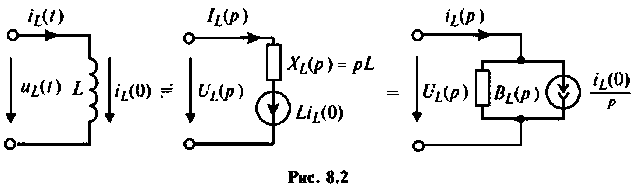
Индуктивность:
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.
Связь между операторным напряжением и током записывается в виде
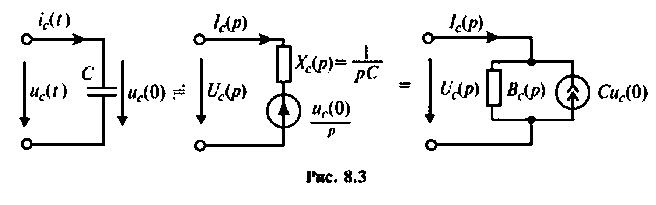
Емкость:
Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.
Связь между напряжением и током устанавливает соотношение
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 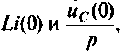
Порядок расчета:
- определяют независимые начальные условия;
- составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
- составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
- для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.
Операторные функции электрических цепей
Основные операторные функции:
Операторной функцией цепи называется отношение изображения по Лапласу выходной величины 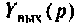
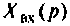
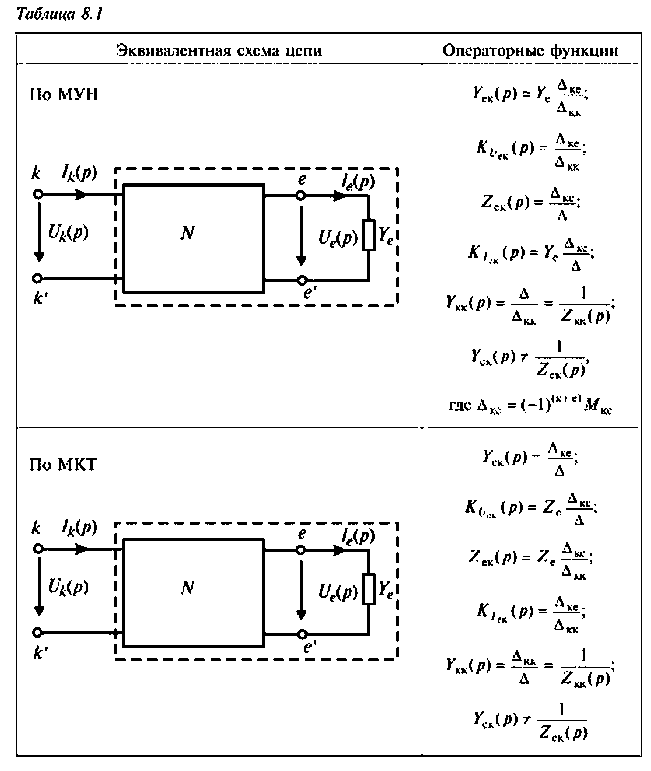
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.
Для расчета операторных функции можно применять все методы расчета комплексных функций
т. е. комплексная функция является частным случаем операторной при замене оператора 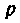
Анализ переходных процессов в цепях с помощью операторных функций
По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие
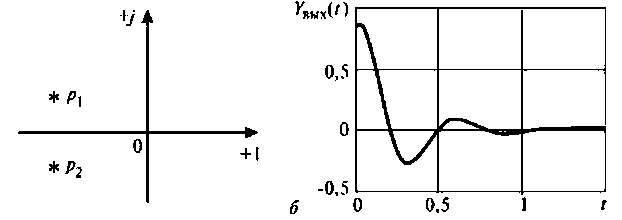
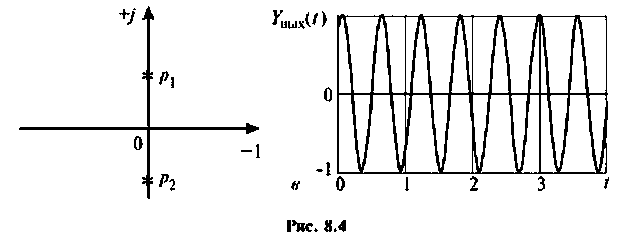
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.
По расположению полюсов операторной функции можно судить о характере переходное процесса:
- если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
- если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
- если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.
Примеры решения задач
Пример 8.4.1.
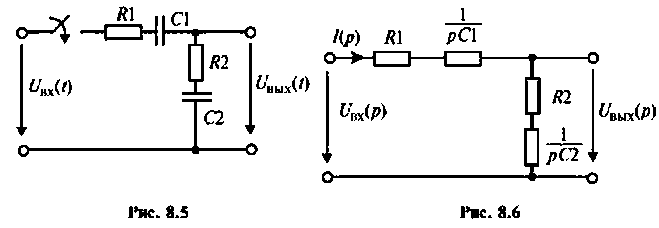
В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение 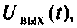
Решение
Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало:
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).
Находят изображение напряжения 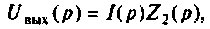
Сопротивление всей цепи определяется выражением
По данному изображению находят оригинал (рис. 8.7) напряжения 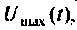
Пример 8.4.2.
К пассивному RС-фильтру нижних частот подключается нагрузка 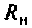
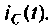
Дано:
Решение
Определяют независимые начальные условия — напряжение на емкости
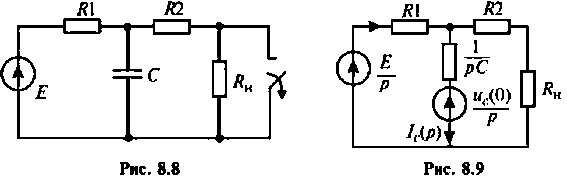
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).
Операторный ток 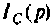
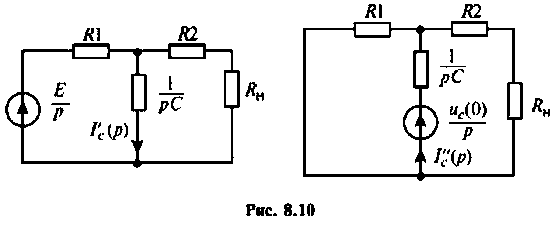
Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.
Искомый ток
Определяют частичный ток
Аналогично определяют частичный ток
По данному изображению 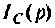
Подставляя числовые значения величин, получают
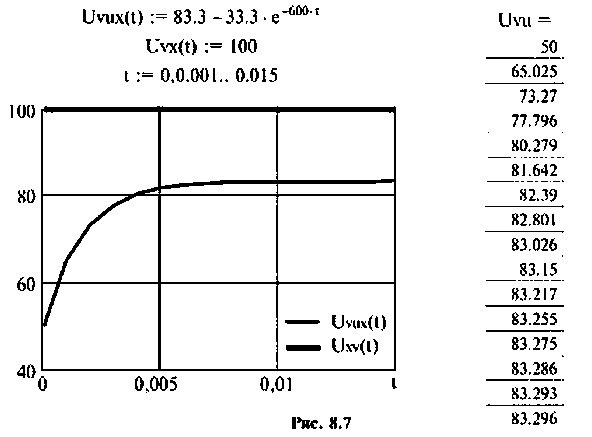
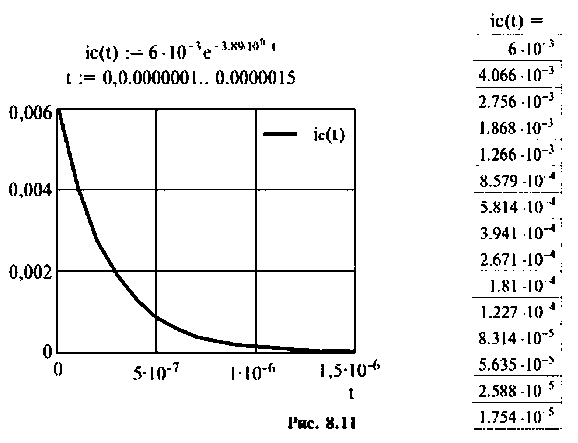
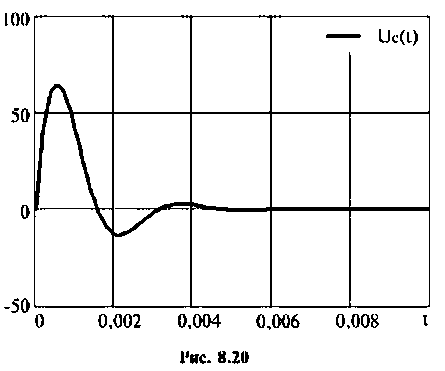
Строят график тока 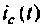
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 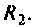
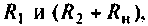
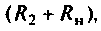
Пример 8.4.3.
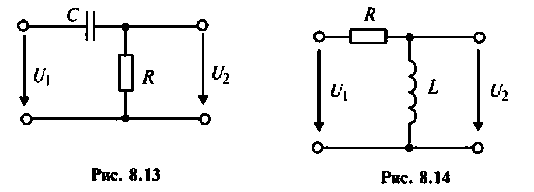
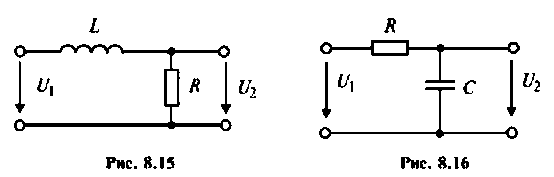
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 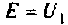
Решение
Применяя преобразования Лапласа, находят изображения
Из прямых преобразований Лапласа и Фурье следует, что
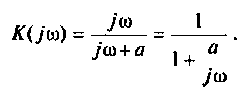
Если принять 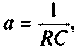
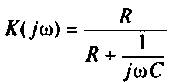
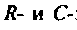
Если принять 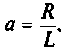
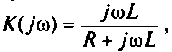
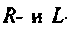
Если принять 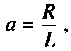
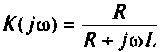
Если принять 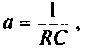
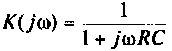
Пример 8.4.4.
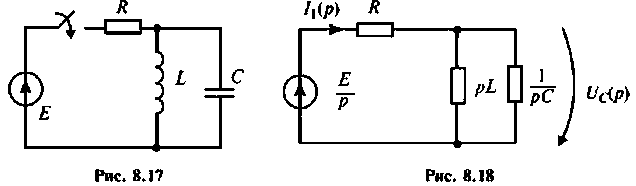
Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение
Определить напряжение на конденсаторе и построить его опюру, если:
Решение
Определяют независимые начальные условия: напряжение на конденсаторе 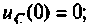
Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).
Находят изображение напряжения на конденсаторе
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции
где 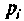
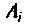
При простых (некратных) полюсах 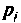
а) Для первого варианта значений:
Полюсы изображения 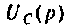
Вычисляют производную 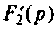
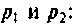
Вычисляют начальные значения компонент
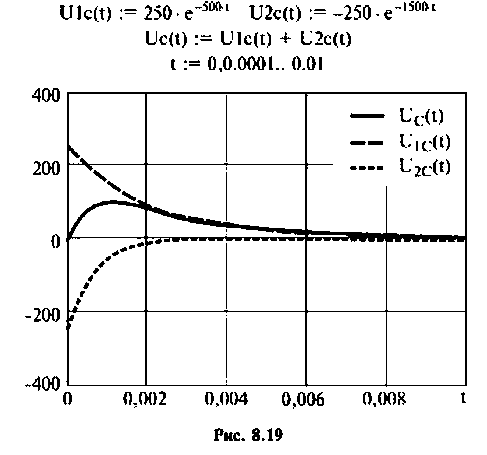
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.
Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде
б) Для второго варианта числовых значений:
а полюсы
Находят производную от 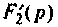
По теореме разложения определяют
где
или
График изменения напряжения 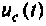
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель 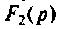
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.
Пример 8.4.5.
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте
а) коэффициент передачи по напряжению 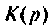
б) характер переходного процесса по кривой переходного процесса.
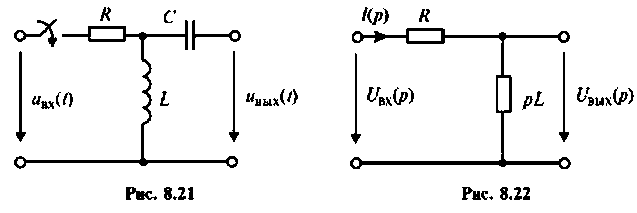
Дано:
Решение
В режиме холостого хода
Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.
Находят изображение напряжения на выходе
Определяют полюсы операторной функции из уравнения 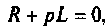
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).
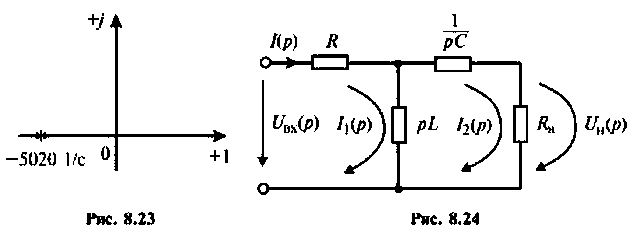
В режиме нагрузки
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).
Определяют операторную функцию 
Определяют полюсы операторной функции из уравнения
Для этога вначале вычисляют L и С.
Находят корни уравнения:
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Метод эквивалентных преобразований. Как находить токи и напряжения в цепиСкачать
Операторные уравнения и схемы замещения элементов цепи
Сущность операторного метода заключается в том, что функции 


Изображение 

 . . | (1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

Следует отметить, что если оригинал 

В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал  | Изображение  |
| A |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:


С использованием этих свойств и данных табл. 1, можно показать, например, что

Изображения производной и интеграла
В курсе математики доказывается, что если 



Таким образом, для напряжения на индуктивном элементе можно записать
или при нулевых начальных условиях

Отсюда операторное сопротивление катушки индуктивности

Аналогично для интеграла: если 

С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:

или при нулевых начальных условиях

откуда операторное сопротивление конденсатора

Закон Ома в операторной форме
Пусть имеем некоторую ветвь 
сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Для мгновенных значений переменных можно записать:

Тогда на основании приведенных выше соотношений получим:

 , , | (2) |
где 
Следует обратить внимание, что операторное сопротивление 


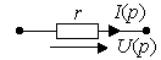
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю

Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде

В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 — 

В первом случае в соответствии с законом Ома 
Во втором случае, т.е. при 
откуда 


Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа

которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:

На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
Например, для изображения тока в цепи на рис. 5 можно записать

Тогда в соответствии с данными табл. 1

что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение 

где 
Это выражение может быть представлено в виде суммы простых дробей
 , , | (3) |
где 

Для определения коэффициентов 


При

Рассматривая полученную неопределенность типа 


Поскольку отношение 

 . . | (4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения 


В заключение раздела отметим, что для нахождения начального 

которые также могут служить для оценки правильности полученного изображения.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные условия?
- Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты ее написания?
С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.
Ответ: 
С использованием предельных соотношений и решения предыдущей задачи найти начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: 
Видео:2 2 Элементы схем замещенияСкачать

Операторные уравнения и схемы замещения элементов цепи
3.5 Расчёт переходных процессов операторным методом
Операторный метод расчета переходных процессов основывается на использовании линейного интегрального преобразования Лапласа
где в качестве параметра участвует комплексная переменная p=s+ jω. Применение этого преобразования сводит функцию времени к зависимости от этого параметра. Большинство исследуемых в электротехнике функций времени имеют в качестве изображения по Лапласу дробно-рациональную функцию, которую называют операторным изображением (см.Таблицу 4), а саму функцию времени — оригиналом. Из приведенных в таблице примеров следует вышеприведенное утверждение, что использование преобразования Лапласа неизбежно сводит любую временную функцию к дробно-рациональной функции вида полином, деленный на полином от переменной p.
Таблица операторных изображений.
Изображение F ( t )
Однотипность получаемых изображений говорит о том, что это преобразование настолько «сильное», что при его использовании любые интегральные и дифференциальные временные соотношения сводятся также к алгебраическим выражениям. Следовательно, применив это преобразование к системе интегро-дифференциальных уравнений, получим систему алгебраических уравнений, зависимых от комплексной переменной p. Этот прием уже был использован ранее при анализе цепей синусоидального тока, где была показана возможность перехода посредством мнимой комплексной переменной jω к комплексным амплитудам токов и напряжений с последующим формальным анализом как бы цепи постоянного тока [1]. Операторный метод является развитием метода комплексных амплитуд, в обоих методах исходные, т.е. временные выражения, заменяют более простыми алгебраическими, которые в данном случае называют операторными.
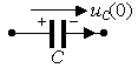
Так же как и в методе комплексных амплитуд, постоянные параметры цепи — r, L, C переходят из оригинала в изображение и обратно без каких-либо изменений в качестве коэффициентов. В комплексном методе производная d/ dt заменяется произведением jω, а в операторном — множителем p; соответственно интеграл во временной области заменяется в комплексном методе на 1/ jω, а в операторном — на 1/p. Вместо комплексных амплитуд напряжения 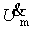
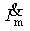
Применяя преобразование Лапласа к компонентным соотношениям (3.5), связывающим токи и напряжения в каждом элементе цепи, можно установить правило перехода от реальной цепи к операторной. Это правило приведено в таблице 5.
Исходная электрическая цепь
Операторная расчетная цепь
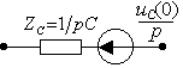
Из таблицы следует, что резистивный элемент r преобразуется в операторный образ без изменения, и закон Ома в операторной форме имеет тот же вид, что и для переменной t: U(p) = rI(p). Индуктивность L заменяется операторным сопротивлением Z L = p L и источником напряжения Li L (0), направление действия которого совпадает с направлением тока в индуктивности к моменту коммутации. Емкость С заменяется операторным сопротивлением Z C = 1/p C и источником напряжения u C (0)/p; направление действия источника противоположно напряжению на емкости к моменту коммутации, т.е. направлено в сторону разряда емкости на внешнюю цепь. Независимые источники энергии заменяются на операторные образы, для чего могут быть использованы изображения функций, указанные в таблице 4. Можно эти изображения найти непосредственно путем использования прямого преобразования Лапласа (3.32). Пользуясь этой таблицей соответствия, легко построить операторную расчетную цепь, которая в дальнейшем рассчитывается как цепь постоянного тока. Из рассмотренного следует, что расчет переходного процесса операторным методом целесообразно начинать сразу с операторной схемы замещения, минуя этап составления системы интегро-дифференциальных уравнений.
Операторная расчетная схема замещения позволяет найти изображения токов и напряжений всех ветвей. Для расчета могут быть применены все известные методы расчета цепей постоянного тока: законы Кирхгофа, метод контурных токов, метод узловых потенциалов, метод наложения, простейшие преобразования и т.д. Компонентные уравнения цепи, связывающие ток и напряжение в каждом элементе или ветви, записываются в операторных образах аналогично цепям постоянного тока [1].Все найденные операторные изображения токов и напряжений имеют однотипный характер в виде дробно-рациональной функции, где полином числителя по степеням p делится на полином знаменателя.
В большинстве случаев выполняется условие n>m, т.е. степень числителя меньше степени знаменателя и дробь правильная. Если же степени равны, то нужно путем деления полиномов выделить целую часть, и от этой части обратное преобразование Лапласа приводит к появлению в решении дельта-функции (см. табл.4,п.3). Та часть решения, которая определяется правильной дробью, позволяет найти оригинал путем применения Теоремы разложения, основанной на возможности представления дробно-рациональной функции в виде суммы простейших дробей. Формула обратного преобразования имеет вид
где p k — корни знаменателя, которые находятся из уравнения F2(p) = 0. Будем рассматривать случай разных вещественных отрицательных корней;
производная от знаменателя по переменной p; F1(p k ) — полином числителя, где вместо p подставлен корень p k .
Часто бывает так, что в полиноме F2(p) слагаемое b0 = 0. Тогда множитель p можно вынести за скобку, и знаменатель принимает вид F2 = p F3. В этом случае при наличии n корней первый корень уравнения p F3(p) = 0 будет нулевым: p1 = 0. Для этого частного случая Теорема разложения принимает вид
т.е. в решении появляется слагаемое, которое не зависит от времени. Это слагаемое соответствует принужденной составляющей искомого тока или напряжения.
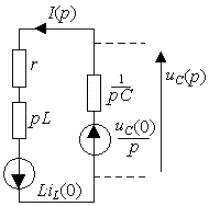
Пример 3.8. Для цепи второго порядка (рис.3.16а), рассмотренной в примере 3.4, найти операторным методом ток и напряжение на емкости после размыкания ключа S. Параметры цепи: E =40 B; r =40 Ом; L = 1 Гн; C = 1/300 Ф.
Решение задачи начинаем с изображения операторной цепи, которая соответствует послекоммутационному состоянию цепи (рис.3.27). Начальные условия для внутренних источников энергии находятся для момента времени t = 0- так же, как это было сделано при решении задачи классическим методом: i L (0-) = E/ r = 1 A; u C (0-) = E = 40 B. В операторной одноконтурной цепи протекает операторный ток I(p) под действием операторных источников напряжения.
Рис. 3.27. Операторная расчетная цепь
Формально рассматривая эту цепь как цепь постоянного тока, найдем
После подстановки численных значений параметров получим
Приравнивая нулю знаменатель, найдем корни
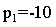
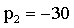
Следует заметить, что знаменатель совпадает с характеристическим полиномом для исследуемой цепи. Именно такое уравнение исследовалось в классическом методе при решении Примера 3.4. Далее найдем производную знаменателя
Применим Теорему разложения и найдем оригинал тока как функцию времени
Полученный ответ полностью совпадает с выражением, полученным ранее.
Операторное напряжение на емкости следует определять как сумму
напряжений непосредственно на сопротивлении Z = 1/p C и на внутреннем
источнике напряжения u C (0-)/p. Для этого можно воспользоваться обобщенной формой закона Ома:
После подстановки числовых данных и приведения подобных получим
Используя те же корни знаменателя, найдем оригинал
Результат с точностью до знака совпадает с ранее полученным выражением. Различие в знаках объясняется другим выбором условного положительного направления напряжения на емкости по сравнению с примером 3.4
Теорема разложения может быть использована и в случае комплексно-сопряженных корней p1 = — β + jω C и p2 = — β — jω C . Рассмотрим этот случай на примере только что решенной задачи с измененным емкостным параметром С = 0.0005 Ф. Аналогично рассмотренному ранее найдем операторный ток
Приравнивая знаменатель к нулю F2(p) = p 2 + 40p + 2000 = 0, найдем корни p1 = -20 + j40 и p2 = -20 — j40, после чего выполним формальную подстановку корней в выражение (3.34):
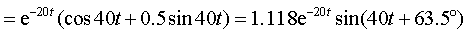
Полученное выражение для тока совпадает с выражением (3.28) не только по форме, но и численно. Особенность математических преобразований заключается в том, что при суммировании двух комплексно-сопряженных выражений вещественные части суммируются, а мнимые взаимно сокращаются. Поэтому для пары комплексно-сопряженных корней результирующее выражение может быть найдено по формуле
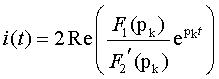
т.е. путем умножения на два вещественной части выражения, которое получается после подстановки в формулу (3.34) любого из комплексно-сопряженных корней. Для рассматриваемого примера и выражения (3.36) применение формулы (3.37) после подстановки первого корня p1 = -20 + j40 даст тот же результат:
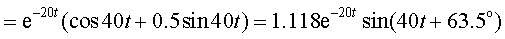
Ответ будет тем же, если вместо первого корня подставим второй корень p2 = -20 — j40.
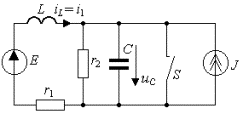
Пример 3.9. В цепи рис.3.28 исследовать переходный процесс после размыкания ключа S. Найти зависимости i1( t) и u C ( t). Параметры цепи: E=100 B; J = 1 A; r1 = r2 = 10 Ом; L = 0,1 Гн; C = 1000 мкФ.
Рис. 3.28. Схема RLC — цепи с двумя независимыми источниками питания.
Решение задачи начинаем с определения основных начальных условий. До коммутации в индуктивности протекал ток i L (0-) = E/ r1 = 10 A, который замыкался через ключ S и короткозамкнутую перемычку. Напряжение на емкости равнялось нулю u C (0-) = 0, так как емкость была подсоединена параллельно короткозамкнутой перемычке. После размыкания ключа к цепи подсоединяется источник тока J, и в цепи развивается переходный процесс с участием индуктивности и емкости.
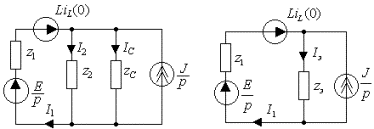
Рис. 3.29. Операторная схема замещения цепи.
а)Исходная цепь. б)Преобразованная цепь.
Операторная схема цепи представлена на рис.3.29а. Следует обратить
внимание на то, что в данном примере не требуется показывать внутренний источник энергии для емкости, т.к. начальные условия на емкости нулевые. Остальные операторные сопротивления равны
Операторная схема цепи формально соответствует разветвленной цепи
постоянного тока, где сопротивления Z2 и Z C соединены параллельно, и их
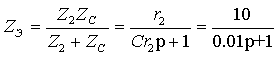
В преобразованной цепи рис.3.29б неизвестны токи I1 и IЭ = I2 + IС . Определим их, составив два уравнения по законам Кирхгофа
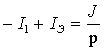
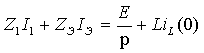
Найдем из системы ток I1:
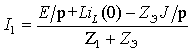
После подстановки в выражение для тока численных значений параметров найдем
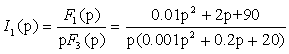
Знаменатель F = p F(p) имеет один нулевой корень p1 = 0 и два комплексно-сопряженных корня p2 = -100 + j100 и p3 = -100 — j100. При наличии нулевого корня целесообразно воспользоваться Теоремой разложения в форме (3.35), а с учетом характера корней окончательно записать форму обратного преобразования в виде (3.37):
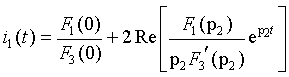
где 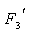
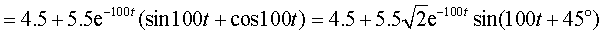
Характер переходного процесса определяется суммой установившегося значения 4,5 A и затухающей синусоиды. Ток начинает свое изменение со значения 10 A и, постепенно колеблясь и затухая, достигает уровня 4,5 A.
Напряжение на емкости в операторной форме найдем по закону Ома
Выполнив все алгебраические преобразования, после подстановки численных значений и применения Теоремы разложения получим
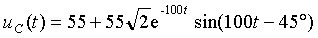
Переходный процесс для емкости начинается с нулевого значения, а затем принимает колебательно-затухающий характер и стремится к уровню 55 B. Тот же результат можно найти путем решения обратной задачи с использованием найденной временной функции i1( t). Для этого следует составить уравнение равновесия для контура, включающего ветви с емкостью и известным током i1:
или
Изучение материала третьего раздела пособия рекомендуется завершить решением задач Приложения 3. Вариант выбирается самостоятельно или указывается преподавателем.
📺 Видео
Урок 146 (осн). Изображение схем электрических цепейСкачать

Длинные линии │Цепи с распределенными параметрами │Теория, часть 1Скачать

Последовательное соединение RLC элементов в цепи синусоидального токаСкачать

Составление схемы простейшей электрической цепиСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Пример 7 | Операторный метод расчета цепи 1-го порядка с конденсаторомСкачать

Пример 1. Операторный метод расчета цепи первого порядка с катушкойСкачать

Идеальные элементы электрической цепи (видео 1) | Анализ цепей | ЭлетротехникаСкачать

Урок 144 (осн). Электрическая цепь и ее составные частиСкачать

Электрическая цепь и ее составные части. Сила тока. Напряжение. 8 класс.Скачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Лекция 092-2. Расчет переходных процессов операторным методом. Операторная схема замещенияСкачать

10-2 Составление схем замещения и расчет несимметричного ТКЗСкачать

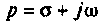
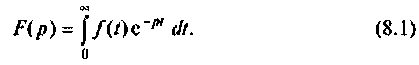
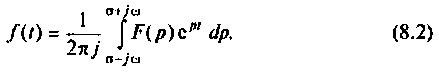
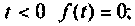
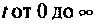 не возрастала быстрее, чем некоторая показательная функция
не возрастала быстрее, чем некоторая показательная функция