Содержание:
Операторные передаточные функции:
Практический смысл и назначение операторного метода в теории электрических цепей состоит, прежде всего, в представлении соотношения вход/выход в операторной форме, что даёт возможность существенно упростить процедуры анализа и синтеза электрических цепей и обеспечить связь между временным и частотным описаниями как колебаний, действующих в цепи, так и самой цепи.
- Законы Ома и Кирхгофа в операторной форме
- Законы Кирхгофа в операторной форме
- Операторные сопротивления и проводимости элементов электрических цепей
- Для элемента активного сопротивления
- Для элемента индуктивности
- Для элемента ёмкости
- Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
- Операторные сопротивление и проводимость двухполюсника общего вида
- Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
- Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
- Связь передаточной функции с частотными и временными характеристиками цепи
- Контрольная работа: Передаточные функции одноконтурной системы
- Операторное уравнение по передаточной функции
- 💡 Видео
Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Законы Ома и Кирхгофа в операторной форме
Покажем, что решение задач анализа колебаний в электрической цепи существенно упрощается при использовании операторного метода.
Законы Кирхгофа в операторной форме
Пусть токи
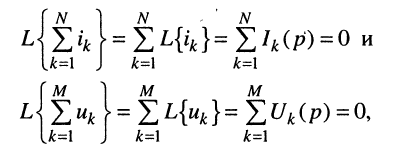
что говорит о формальной справедливости законов Кирхгофа для токов и напряжений, выраженных в операторной форме.
Операторные сопротивления и проводимости элементов электрических цепей
Убедимся в справедливости закона Ома для L-изображений колебаний на зажимах элементов R, L, С при нулевых начальных условиях (см.разд. 15.2) и найдём операторные изображения 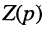
Для элемента активного сопротивления
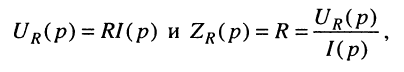
т. е. операторное активное сопротивление равно самому активному сопротивлению, поэтому операторная активная проводимость равна самой активной проводимости
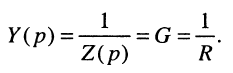
Для элемента индуктивности
правило дифференцирования даёт:
откуда операторные сопротивление и проводимость индуктивности равны:
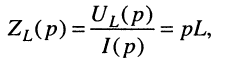
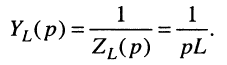
Для элемента ёмкости
правило интегрирования даёт:
откуда операторные сопротивление и проводимость ёмкости равны:
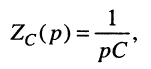
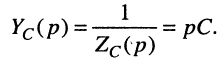
Заметим, что поскольку оператор р согласно (16.2) определён как комплексное переменное
операторные сопротивления и проводимости элементов L и С получаются заменой оператора 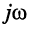
Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
Закон Ома при нулевых начальных условиях формально верен и для сложных двухполюсников, если в числе их элементов не содержатся независимые источники.
Определение:
Операторным сопротивлением 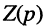
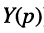
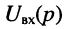
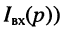
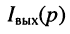
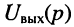
(соответственно 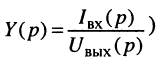
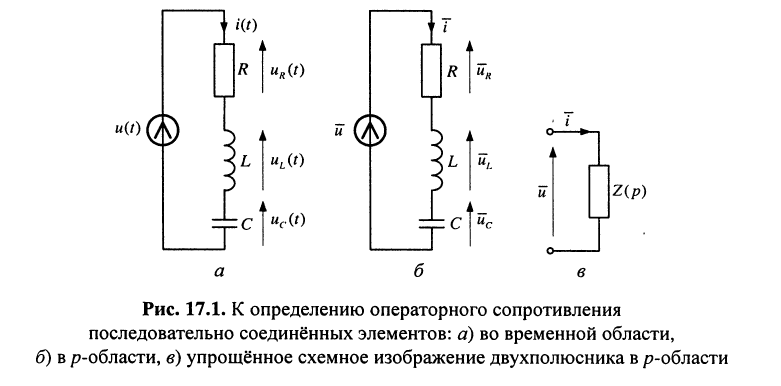
Найти операторное сопротивление двухполюсника (рис. 17.1), состоящего из последовательно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Напряжение на зажимах двухполюсника при нулевых начальных условиях равно
Применим к полученному уравнению преобразование Лапласа:
откуда следует, что при последовательном соединении элементов их операторные сопротивления складываются, как и для комплексных сопротивлений, но оператор 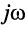
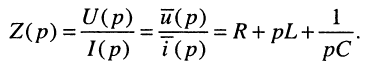
Пример 17.2.
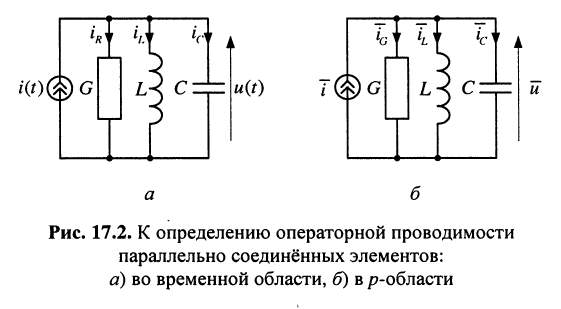
Найти операторную проводимость двухполюсника (рис. 17.2), состоящего из параллельно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Для тока 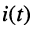
поэтому операторную проводимость заданного двухполюсника можно записать сразу:
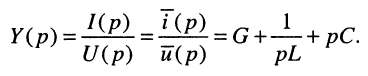
В силу дуальности последовательного и параллельного контуров выражение (17.9) можно было записать сразу на основании формулы (17.8).
Выражения (17.8) и (17.9) представляют собой входные операторные функции цепи. Они дают основания определению операторного сопротивления и проводимости двухполюсника общего вида.
Операторные сопротивление и проводимость двухполюсника общего вида
Закон Ома, при нулевых начальных условиях, формально можно применить и для сколь угодно сложных двухполюсников. Ранее
(см. лекцию 5) было установлено, что если на входе двухполюсника действует источник напряжения с ЭДС 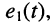
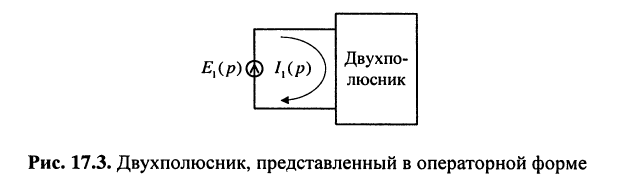
Переходя к L-изображениям напряжений, токов и сопротивлений элементов цепи, получим представление двухполюсника в операторной форме (рис. 17.3), что позволяет записать L-изображение входного тока:
Теперь согласно определению операторной проводимости и операторного сопротивления имеем:
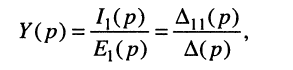
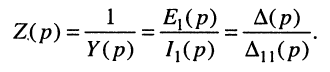
При этом нужно помнить, что определители и алгебраические дополнения в таких формулах записываются с учётом свойств преобразования Лапласа, как это сделано в примерах 17.1 и 17.2.
Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
В лекции 15 было показано, что во временной области соотношение вход/выход линейной электрической цепи при произвольном воздействии описывается уравнением свёртки:
где h(t) — импульсная характеристика, x(t) — воздействие, y(t) — реакция. При этом воздействие и реакция могут быть напряжениями или токами.
Для описания соотношения вход/выход в операторной форме воспользуемся L-изображением свёртки
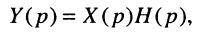
откуда получаем соотношения вход/выход в операторной форме
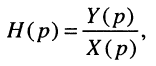
которое называют передаточной функцией.
Определение:
Передаточной функцией линейной электрической цепи называется отношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.
Выражение (17.13) говорит о том, что передаточная функция является L-изображением импульсной характеристики, т. е. импульсная характеристика является обратным преобразованием Лапласа передаточной функции:
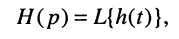
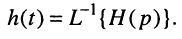
Именно этими зависимостями объясняется содержащееся в определении передаточной функции требование нулевых начальных условий.
Связь между передаточной функцией и переходной характеристикой можно установить, если воспользоваться интегралом Дюамеля (15.20а) при нулевых начальных условиях:
когда 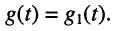
Первый сомножитель правой части полученного уравнения содержит L-изображение производной, поэтому окончательно можно записать:
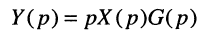
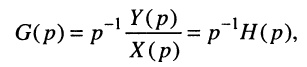
что полностью соответствует связи импульсной и переходной характеристик (15.16).
Обратим внимание на то, что передаточная функция может быть получена из комплексных частотных характеристик формальным образом, а именно — простой заменой в КЧХ 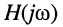
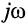
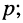
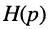
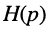
В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве реакции цепи, различают четыре вида передаточных функций:
операторное передаточное сопротивление
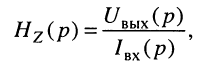
операторную передаточную проводимость
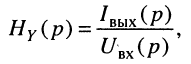
передаточную функцию по току
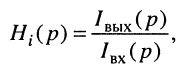
передаточную функцию по напряжению
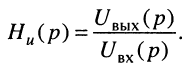
Последние две функции иногда называют операторными передаточными коэффициентами по току и по напряжению соответственно.
По любой из передаточных функций (17.18)—(17.21) нетрудно найти L-изображение реакции цепи, а затем и саму реакцию на заданное воздействие, поскольку любая передаточная функция Н(р) согласно (17.12) может рассматриваться как связующий коэффициент между L-изображения ми воздействия Х(р) и реакции Y(p).
Пример 17.3.
Записать передаточную функцию для последовательного колебательного контура (рис. 17.1, б) относительно напряжения на индуктивности.
Решение. По определению передаточной функции для индуктивности имеем
Но операторное напряжение на индуктивности равно:
Подставляя сюда операторное сопротивление (17.8), получаем искомую передаточную функцию:
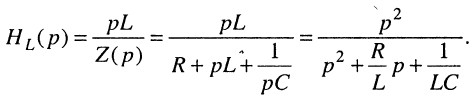
Аналогично можно получить и другие передаточные функции для последовательной, параллельной или более сложной цепи. В последнем случае потребуется составить систему уравнений для L-изображений колебаний, воспользовавшись методом контурных токов или узловых напряжений.
Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
Задача 17.1.
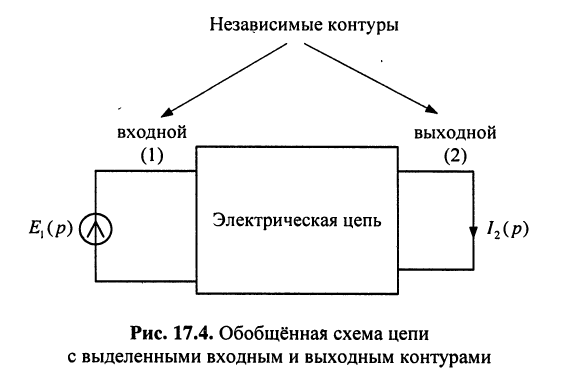
Получить и исследовать общее выражение для передаточной функции цепи, когда воздействие представляет собой ЭДС источника напряжения, а реакцией является ток в выделенной ветви анализируемой цепи (рис. 17.4).
Решение. Выберем независимые контуры в цепи так, чтобы через источник напряжения замыкался ток только одного входного контура, а через интересующую нас ветвь — ток только одного выходного контура. На рис. 17.4 они обозначены индексами 1 и 2 соответственно.
Теперь, как и в задаче 5.2, необходимо положить 
откуда по определению передаточной функции имеем операторную передаточную проводимость
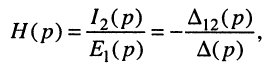
где 
a 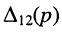
Заметим, что определитель и все его миноры представляют собой рациональные функции оператора р, все коэффициенты которых являются вещественными числами. Это объясняется тем, что при раскрытии определителя над его элементами совершаются только операции умножения, сложения и вычитания, а сами элементы представляют собой простейшие рациональные
функции с вещественными коэффициентами вида (17.11). Раскрывая определитель 
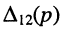
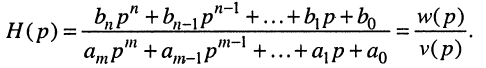
Полиномы числителя 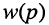
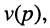
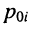
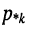
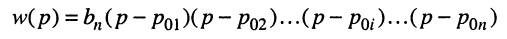
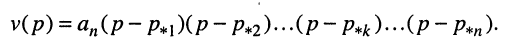
Отсюда передаточная функция (17.24) приобретает вид:
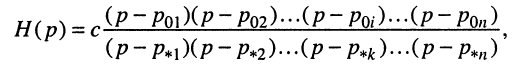
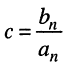
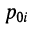
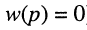
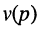
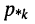
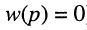
Названия корней уравнения 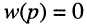
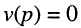
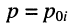
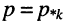
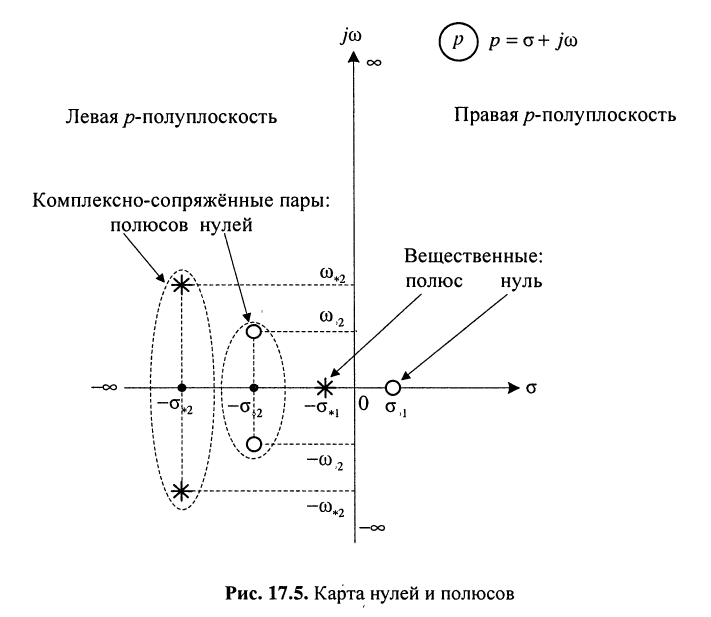
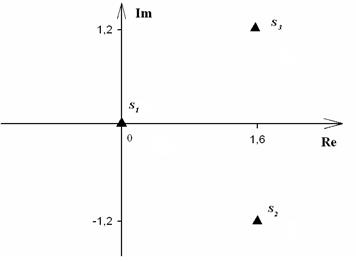
Нули и полюсы наглядно отображаются на комплексной p -плоскости (рис. 17.5) значками ( ° ) и ( * ) соответственно.
На рис. 17.5 показаны:
- вещественный положительный нуль
и отрицательный полюс
у которых частота
- пара комплексно-сопряжённых нулей
и
и пара комплексно-сопряжённых полюсов
и 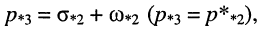
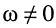
Отображение нулей и полюсов на p-плоскости называют картой нулей и полюсов. Различают левую и правую р-полуплоскости.
Карта нулей и полюсов позволяет оценить ряд свойств электрической цепи и, в частности, определить её устойчивость с точки зрения устойчивости передаточной функции.
Утверждение:
цепь является строго устойчивой тогда и только тогда, когда её передаточная функция имеет, полюсы только в левой р-полуплоскости, исключая мнимую ось.
Доказательство. Напомним, что цепь называется строго устойчивой, если при нулевых начальных условиях ограниченное по величине воздействие
вызывает ограниченную по величине реакцию
Но реакцию y(t) при нулевых условиях можно найти с помощью уравнения свёртки
Отсюда при заданных ограничениях имеем соотношение
из которого следует, что для получения равномерно ограниченной для всех t реакции, т. е. для обеспечения строгой устойчивости цепи должно выполняться условие абсолютной сходимости интеграла от импульсной характеристики:
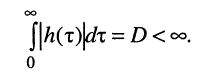
Найдём расположение полюсов, которое соответствует полученному условию. Для этого представим импульсную характеристику h(t) цепи как обратное L-изображение передаточной функции (17.15) путём разложения последней на сумму простых дробей (16.28):
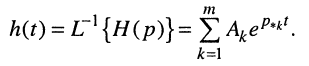
Подставим в интеграл (17.28) правую сумму (17.29)
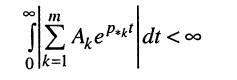
и проведём ряд несложных преобразований.
Поскольку модуль суммы не превосходит суммы модулей, справедливо следующее неравенство:
В правой части полученного неравенства поменяем местами знаки суммирования и интегрирования и оставим только знак равенства:
Рассмотрим интеграл в правой части равенства, содержащий модуль экспоненты, при
во-вторых, первая экспонента под интегралом всегда неотрицательна, поэтому знак модуля можно опустить:
Остаётся исследовать сходимость интеграла при положительном и отрицательном показателе
Сходимость интеграла при 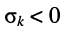
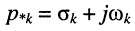
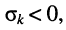
Связь передаточной функции с частотными и временными характеристиками цепи
Как было показано в лекции 10, для определения частотных характеристик АЧХ 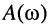
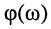
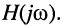
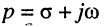
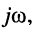
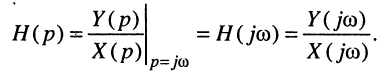
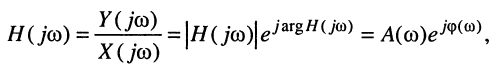
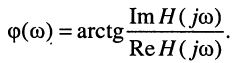
Эквивалентное выражение для КЧХ получается из (17.31), если воспользоваться комплексными функциями числителя и знаменателя:
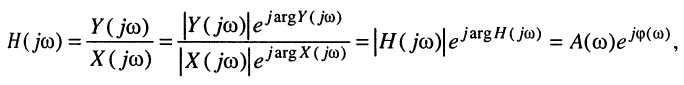
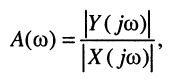
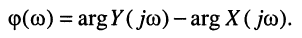
Вследствие того, что функция
является иррациональной, обычно при анализе и синтезе цепей используют квадрат АЧХ:
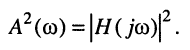
Перечислим основные свойства передаточных функций и квадрата АЧХ пассивных цепей.
- Передаточная функция является L-изображением импульсной характеристики.
- Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами.
- Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
- Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей; приневыполнении этого свойства АЧХ на бесконечно больших частотах
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
- Частотные характеристики цепи вычисляются по передаточной функции при подстановке
- Квадрат АЧХ является чётной рациональной функцией переменной с вещественными коэффициентами:
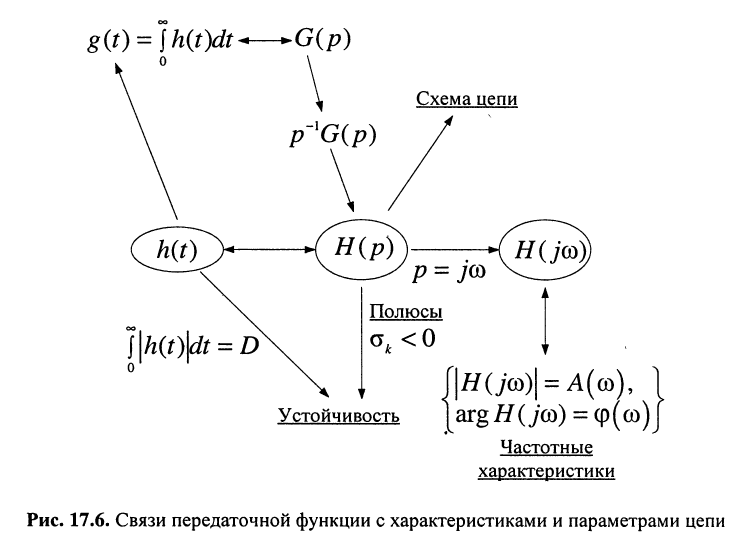
- По передаточной функции можно изобразить схему цепи
Обобщённая схема связи передаточной функции с характеристиками и свойствами цепи представлена на рис. 17.6.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Контрольная работа: Передаточные функции одноконтурной системы
| Название: Передаточные функции одноконтурной системы Раздел: Рефераты по математике Тип: контрольная работа Добавлен 21:52:15 24 декабря 2010 Похожие работы Просмотров: 508 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать |
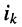
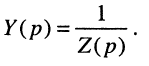
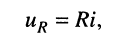
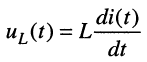
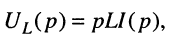
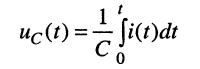
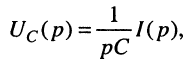
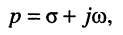
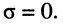
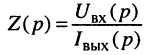
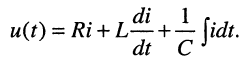
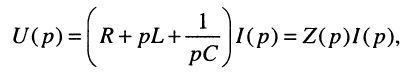
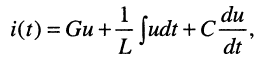
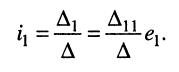
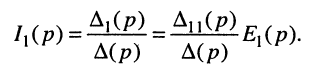
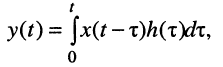
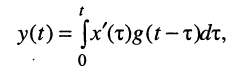
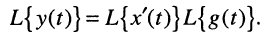
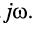
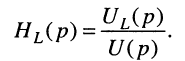
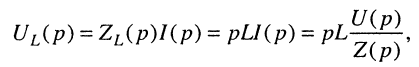
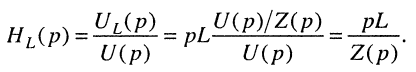
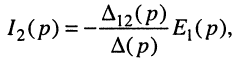
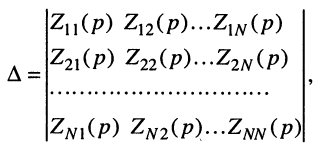
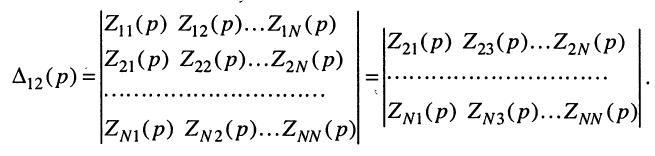
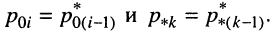
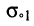 и отрицательный полюс
и отрицательный полюс 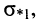 у которых частота
у которых частота 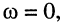
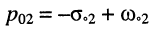 и
и 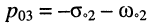
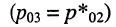 и пара комплексно-сопряжённых полюсов
и пара комплексно-сопряжённых полюсов 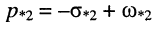
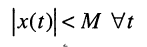
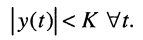
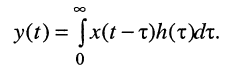
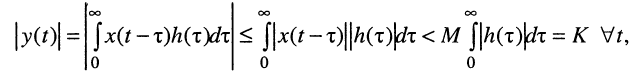
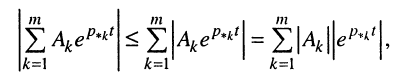
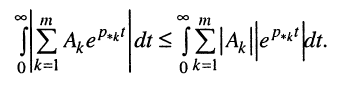
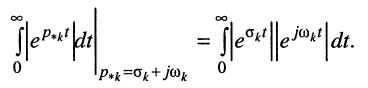
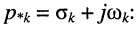
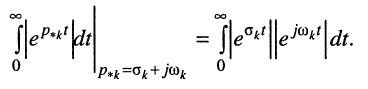
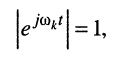
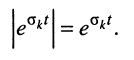
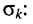
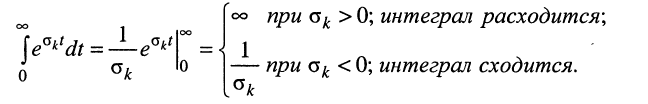
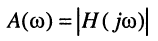
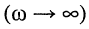 должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.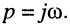
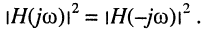
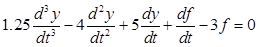 ; б)
; б)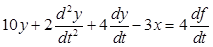 .
.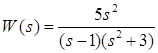 .
.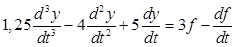 .
. .
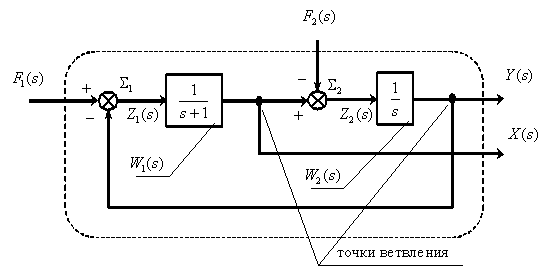
. , то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.
, то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.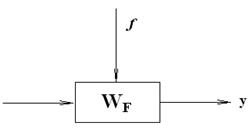
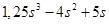 .
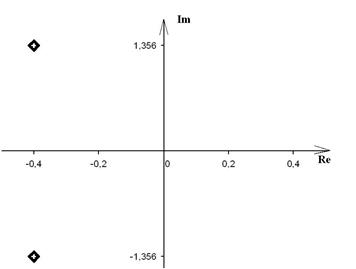
.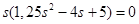 , корни которого:
, корни которого: ,
, 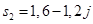 и
и 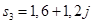 .
.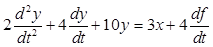 .
.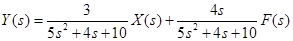 .
.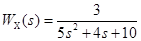 и
и  ,
,
 ,
, .
.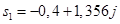 и
и 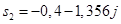 .
.
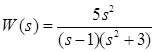
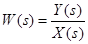 , получим:
, получим: , тогда:
, тогда: .
.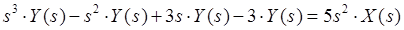
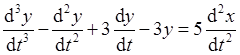 .
.
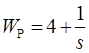 ;
;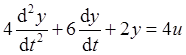 .
.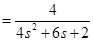 .
.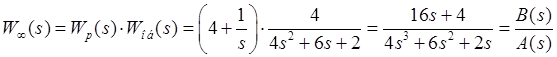
 ;
;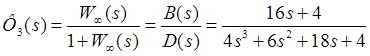 — по заданию;
— по заданию;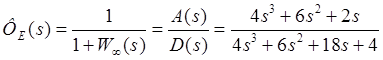 — по ошибке;
— по ошибке;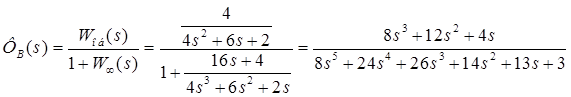 — по возмущению.
— по возмущению.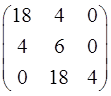
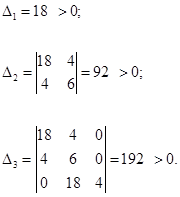


 и
и  , линейно, то говорят о линейном динамическом звене
, линейно, то говорят о линейном динамическом звене
 — постоянные коэффициенты,
— постоянные коэффициенты,  .
. .
.

 ), имеет вид дробно-рациональной функции.
), имеет вид дробно-рациональной функции. .
. ,
,

 ,
,


 .
. .
.
 .(5)
.(5)





 .
. ,
, описывает суммирующее звено
описывает суммирующее звено  . Таким образом, получены два фрагмента структурной схемы
. Таким образом, получены два фрагмента структурной схемы
 .
. ,
, описывает суммирующее звено
описывает суммирующее звено  . Таким образом, получены еще два фрагмента структурной схемы
. Таким образом, получены еще два фрагмента структурной схемы
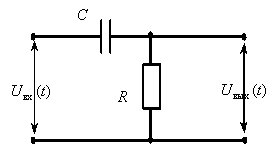
 , обозначая ее как
, обозначая ее как  . При этом схема эксперимента имеет вид
. При этом схема эксперимента имеет вид 


 .
.
 ,
, преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,
преобразуем (5), используя теорему об умножении изображений преобразования Лапласа, ,
, , тогда
, тогда .
. , обозначая ее как
, обозначая ее как  . При этом схема эксперимента имеет вид
. При этом схема эксперимента имеет вид 


 .
.
 .
.
 .
.
 .
.